一种轨迹跟踪控制的变论域模糊控制系统及控制方法与流程

本发明涉及多关节机器人的控制技术领域，尤其是一种变论域模糊控制器及使用该控制器的控制方法。

背景技术：

机械臂轨迹跟踪控制是通过控制器对机械臂各关节施加控制力矩来实现对关节轨迹的跟踪，使得机械臂在实际运动过程中的关节角位移变量均与设定的关节角位移的值相吻合，最终使机械臂末端顺利地完成指定的作业流程。由于机械臂自身的物理参数受负载变化的影响以及关节间的耦合性等，使得建立机械臂的精确数学模型存在不确定性，这在一定程度上明显影响了机械臂的实际控制效果，因此，机械臂轨迹跟踪控制的目标是以较低的偏差对期望关节轨迹进行跟踪。

模糊控制方法不依赖被控对象的精确数学模型，尤其适合机械臂轨迹跟踪控制。但在设计模糊控制器时要解决获得满意控制精度和减少规则数目以降低控制算法复杂性的两个主要问题，导致模糊控制器精度不高的主要原因是控制器缺乏积分环节和控制规则数量有限。为此，一些学者提出了一些解决方案，其中，李洪兴提出了变论域模糊控制方法。变论域模糊控制算法的核心思想是,通过一组非线性伸缩因子在线调节论域，通过论域随偏差和偏差变化率的变化而变化来减少初始控制规则的数量，并使论域划分在期望控制点附近变得非常精细，实现自适应与高精度的控制目的。可见，控制精度与伸缩因子的设计有很大关系，设计合适的伸缩因子是变论域模糊控制器设计的关键环节。现有的伸缩因子的类型主要有比例型、积分型和指数型，这些类型的伸缩因子没有充分考虑到偏差和偏差变化率同时变化时的相关性，以及这种相关性对机械臂轨迹跟踪的变论域模糊控制器在线调节作用产生的影响。

技术实现要素：

本发明的目的是针对多关节机器人提出一种新的轨迹跟踪控制的变论域模糊控制系统，以能够提高多关节机器人的末端轨迹控制精度。

本发明同时提供了采用上述控制系统的控制方法。

本实现上述目的，本发明采用如下技术方案：

一种轨迹跟踪控制的变论域模糊控制系统，用于多关节机械臂轨迹跟踪的变论域模糊控制；包括输入模块、输出模块、变论域模糊控制器、混合伸缩因子控制模块；

所述输入模块用于输入机械臂多个关节的期望关节角度qdn，其中n为正整数，表示机械臂关节数量；

所述变论域模糊控制器采用两输入单输出的模糊控制器，表示为：

由该式获得k+1时刻变论域模糊控制器的输出变量un的值通过比例因子kun将转化为作用于机械臂关节的力矩τn值，

式中，j表示变论域模糊控制器规则表中第j条控制规则；en代表经过量化因子作用后的无量纲的关节角度偏差，en＝ken·(qdn-qn)；ecn代表经过量化因子作用后的关节角度偏差变化率，为k时刻输入变量en的模糊子集，为模糊子集的隶属函数，表征k时刻输入变量en的值隶属于模糊子集的隶属度；为k时刻输入变量ecn的模糊子集，为模糊子集的隶属函数，表征k时刻输入变量ecn的值隶属于模糊子集的隶属度；为k时刻对应的输出论域模糊子集的中心；

混合伸缩因子控制模块包括关节角度偏差的伸缩因子α1(en)、偏差变化率的伸缩因子α2(en,ecn)、输出力矩的伸缩因子β(un)；其中α1(en)用以在线地调整输入变量en的论域；α2(en,ecn)用以在线地调整输入变量ecn的论域；β(un)用以在线地调整输入变量un的论域；

其中，

式中，e、ec分别为输入变量en和ecn的初始论域；u为输出变量un的初始论域；动态权值参数ρ为带宽；参数ε称为贴现因子，ε∈(0,1)；δ为充分小的正数；

根据动力学方程以及所设计的轨迹跟踪控制的变论域模糊控制器的输出τn，获得各关节实时采样输出的仿真关节角度；输出模块即用以输出机器人n个关节的仿真关节角度。

有益效果：与现有技术相比，轨迹跟踪控制的变论域模糊控制系统的动态响应快，稳态精度高，具有更好的控制效果，显示了比例-指数混合型伸缩因子在机械臂轨迹跟踪控制中的有效性和优越性。

而采用本发明中轨迹跟踪控制的变论域模糊控制系统的控制方法可采用以下技术方案：

首先将k时刻模糊控制器的输入变量值转化为模糊量，并由所选取的隶属度函数计算得出隶属于不同模糊量的隶属度；然后确定模糊规则，选取模糊推理方法和解模糊化方法确定模糊控制器表达式f(en,ecn,un)，由该式计算得到k+1时刻输出变量un的值最后通过比例因子kun将转化为作用于机械臂关节的力矩τn值；在控制过程中，利用伸缩因子α1(en)、α2(en,ecn)和β(un)的作用在线地调整输入变量en、ecn与输出变量un的论域；输入论域可随en、ecn的减小而收缩或随en、ecn的增大而膨胀，同样，输出论域亦可随un的减小而收缩或随un的增大而膨胀。

附图说明

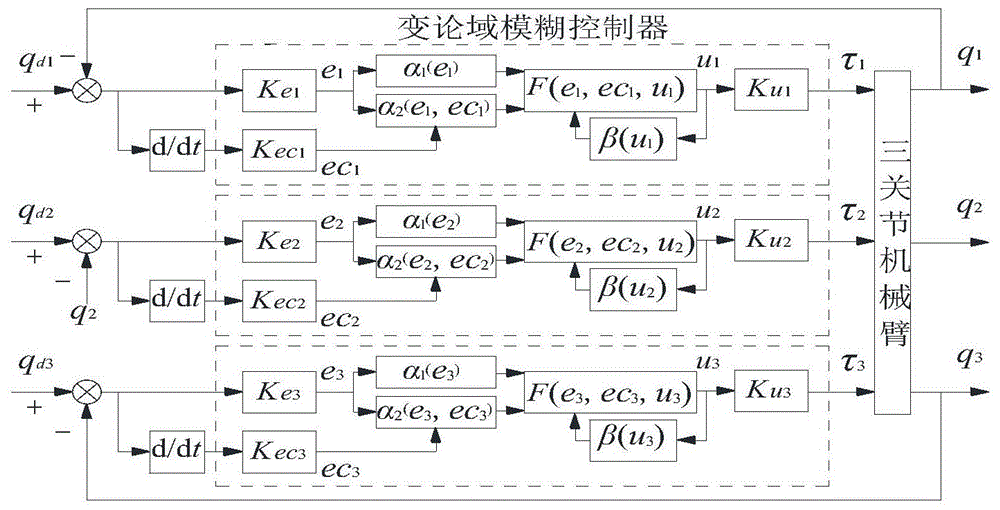
图1三关节机械臂轨迹跟踪控制的变论域模糊控制系统的结构示意图；

图2是三关节机械臂中关节1、2、3分别使用混合型伸缩因子与指数型伸缩因子的变论域模糊控制器跟踪机械臂期望关节轨迹图；

图3是三关节机械臂中关节1分别使用混合型伸缩因子与指数型伸缩因子的变论域模糊控制器跟踪机械臂期望关节轨迹所获得的关节角度的对比图；

图4是三关节机械臂中关节2分别使用混合型伸缩因子与指数型伸缩因子的变论域模糊控制器跟踪机械臂期望关节轨迹所获得的关节角度的对比图；

图5是三关节机械臂中关节3分别使用混合型伸缩因子与指数型伸缩因子的变论域模糊控制器跟踪机械臂期望关节轨迹所获得的关节角度的对比图；

图6三关节机械臂笛卡尔空间分别使用混合型伸缩因子与指数型伸缩因子的变论域模糊控制器跟踪机械臂期望关节轨迹所获得的轨迹误差示意图。

具体实施方式

下面结合附图对本发明进一步说明：

请参阅图1所示，本发明公开一种轨迹跟踪控制的变论域模糊控制系统，用于多关节机械臂轨迹跟踪的变论域模糊控制。

包括输入模块、输出模块、变论域模糊控制器、混合伸缩因子控制模块；

所述输入模块用于输入机械臂多个关节的期望关节角度qdn，其中n为正整数，表示机械臂关节数量；

所述两输入单输出的变论域模糊控制器可表示为：

通过比例因子kun将转化为作用于机械臂关节的力矩τn值，

式中，j表示变论域模糊控制器规则表中第j条控制规则；en和ecn分别代表经过量化因子作用后的无量纲的关节角度偏差和关节角度偏差变化率；为k时刻输入变量en的模糊子集，为模糊子集的隶属函数，表征k时刻输入变量en的值隶属于模糊子集的隶属度；为k时刻输入变量ecn的模糊子集，为模糊子集的隶属函数，表征k时刻输入变量ecn的值隶属于模糊子集的隶属度；为k时刻对应的输出论域模糊子集的中心；公式中的数据25为该模糊控制器的模糊规则条数，是根据两个输入变量的模糊集个数决定的。两个输入变量的模糊集个数都为5，所以模糊规则数为5×5＝25。

混合伸缩因子控制模块包括关节角度偏差的伸缩因子α1(en)、偏差变化率的伸缩因子α2(en,ecn)、输出力矩的伸缩因子β(un)；其中α1(en)用以在线地调整输入变量en的论域；α2(en,ecn)用以在线地调整输入变量ecn的论域；β(un)用以在线地调整输入变量un的论域；

其中，

式中，e、ec分别为输入变量en和ecn的初始论域；u为输出变量un的初始论域；动态权值参数ρ为带宽；参数ε称为贴现因子，ε∈(0,1)；δ为充分小的正数；

输出模块用以输出的机器人n个关节的仿真关节角度。

忽略摩擦力以及机械臂末端负载，用牛顿-欧拉方程对三关节机械臂进行分析，动力学方程表达形式如下：

式中γ代表机械臂的关节力矩向量，即γ＝[τ1,τ2,τ3]^t，q代表机械臂关节角度向量，代表机械臂关节角速度向量，代表机械臂关节角加速度向量，m(q)是3×3阶的机械臂惯性矩阵,b(q)是3×3阶的哥氏力系数矩阵，是3×1阶的关节速度积矢量，即c(q)是3×3阶的离心力系数矩阵，而是3x1阶矢量，即g(q)是3×1阶的重力矢量。机械臂动力学方程描述了力矩γ与各关节角度q、角速度以及角加速度之间的关系，同时关节角度、角速度以及角加速度，结合机器人运动学和质量分布方面的知识，在已知力矩γ的情况下，可计算出各关节角度q、角速度以及角加速度以三关节机械臂仿真数学模型为例，矩阵m(q)表示为：

其中，

a11＝im1+i1+i3·cc2+i7·ss23+i10·sc23+i11·sc2+i21·ss23+2[i5·c2.s23+i12·c2·c23+i15·ss23+i16·c2.s23+i22·sc23]

a12＝i4·s2+i8·c23+i9·c2+i13·s23-i18·c23

a13＝i8·c23+i13·s23-i18·c23

a22＝im2+i2+i6+2[i5·s3+i12·c2+i15+i16·s3]

a23＝i5·s3+i6+i12·c3+i16·s3+2i15

a33＝im3+i6+2i15

a21＝a12,a31＝a13,a32＝a23

矩阵b(q)表示为：

其中，

b112＝2[-i3·sc2+i5·c223+i7·sc23-i12·s223+2i15·sc23+i16·c223+i21·sc23+i22·(1-2ss23)]+i10·(1-2ss23)+i11·(1-2ss2)

b113＝2[i5·c2·c23+i7·sc23-i12·c2·s23+2i15·sc23+i16·c2·c23+i21·sc23+i22·(1-2ss23)]+i10·(1-2ss23)

b214＝i14·s23+i19·s23+i20·s23

b314＝i20·s23+i14·s23+i19·s23

矩阵c(q)表示为：

其中，

c12＝i4·c2-i8·s23-i9·s2+i13·c23+i18·s23

c13＝0.5·b123＝-i8·s23+i13·c23+i18·s23

c21＝-0.5·b112＝i3·sc2-i5·c223-i7·sc23+i12·s223-2i15·sc23-i16·c223-i21·sc23-i22·(1-2ss23)-0.5·i10·(1-2ss23)-0.5·i11.(1-2ss2)

c23＝0.5·b223＝-i12·s3+i5·c3+i16·c3

c31＝-0.5·b113＝-i5·c2·c23-i7·sc23+i12·c2·s23-2i15·sc23-i16·c2·c23-i21·sc23--i22·(1-2ss23)-0.5·i10·(1-2ss23)

c32＝-c23＝i12·s3-i5·c3-i16·c3

矩阵g(q)表示为：

其中，

g′2＝g1·c2+g2·s23+g3·s2

g′3＝g2·s23

在上述等式中，in和gn代表动力学方程中出现的计算常数值，in代表惯性常数值，gn代表重力常数值，它们是通过机器人质量分布方面的知识得到的，具体数值如表1所示。上述等式中的si、ci以及cci等均是缩写形式，即：

si＝sin(qi),ci＝cos(qi),cij＝cos(qi+qj)

cci＝cos(qi)·cos(qi),csi＝cos(qi)·sin(qi)

sijk＝sin(qi+qj+qk)

表1计算常数值

在图1中以针对三关节机器人的控制系统为例，图中各符号的下标n＝1,2,3表示机械臂关节数量；qdn表示机械臂三个关节的期望关节角度；qn表示输出的三个关节的仿真关节角度；d/dt表示图中虚线部分表示变论域模糊控制器，常数ken和kecn分别代表偏差和偏差变化率的量化因子；变量en和ecn分别代表经过量化因子作用后的无量纲的关节角度偏差和关节角度偏差变化率；α1(en)定义为关节角度偏差的伸缩因子，α2(en,ecn)定义为偏差变化率的伸缩因子，β(un)定义为输出力矩的伸缩因子；f(en,ecn,un)是用于计算变量un值的函数；变量un表示无量纲的输出力矩；常数kun称为变量un的比例因子；τn表示作用于机械臂三个关节的力矩。

核心部分的模糊控制器具体控制原理为：首先将k时刻模糊控制器的输入变量值转化为模糊量，并由所选取的隶属度函数计算得出隶属于不同模糊量的隶属度；然后确定模糊规则，选取模糊推理方法和解模糊化方法确定模糊控制器表达式f(en,ecn,un)，由该式计算得到k+1时刻输出变量un的值最后通过比例因子kun将转化为作用于机械臂关节的力矩τn值。在控制过程中，利用伸缩因子α1(en)、α2(en,ecn)和β(un)的作用在线地调整输入变量en、ecn与输出变量un的论域。输入论域可随en、ecn的减小而收缩或随en、ecn的增大而膨胀，同样，输出论域亦可随un的减小而收缩或随un的增大而膨胀。

本申请将三关节机械臂的输入变量en和ecn的模糊集取为{fd，fx，l，zx，zd}，即{负大，负小，零，正小，正大}；输出变量un的模糊集取为{fd，fz，fx，l，zx，zz，zd}，即{负大，负中，负小，零，正小，正中，正大}；设计出如表3所示的具有25条控制规则的变论域模糊控制器规则表。输入变量en、ecn与输出变量un的隶属函数取三角形隶属函数如表2所示。取量化因子ke1＝9，ke2＝14，ke3＝4；kec1＝7，kec2＝9，kec3＝3；取比例因子ku1＝7.5，ku2＝6，ku3＝5，采用强度转移模糊推理法和中心平均解模糊法确定模糊控制器表达式的形式为：

式中，j表示表3中第j条控制规则(j＝1,2,…,25)；为k时刻输入变量en的模糊子集，为模糊子集的隶属函数，表征k时刻输入变量en的值隶属于模糊子集的隶属度；同理，为k时刻输入变量ecn的模糊子集，为模糊子集的隶属函数，表征k时刻输入变量ecn的值隶属于模糊子集的隶属度；为k时刻对应的输出论域模糊子集的中心。

表2变论域模糊控制器输入输出变量论域及其隶属函数

表3模糊规则表

伸缩因子的选取作为变论域模糊控制器设计中的关键环节，不同类型、不同参数的伸缩因子所产生的效果大相径庭。考虑关节角度偏差en和关节角度偏差变化率ecn之间的相关性对控制精度的影响，本申请将偏差变化率的伸缩因子设计为与en和ecn二者相关的比例-指数型混合伸缩因子，取为en和ecn的动态加权二元函数，动态权值是一个以en为自变量且包含可调参数ρ的指数函数。通过w^k的动态调节作用，可以实时调节en和ecn对的影响程度。一般地，伸缩因子满足对偶性、避零性、单调性、协调性、正规性，本申请提出的混合伸缩因子满足这些特性。由上述对伸缩因子的分析，将关节角度偏差的伸缩因子关节角度偏差变化率的伸缩因子以及输出力矩的伸缩因子分别设计为如下形式：

式中，e、ec分别为输入变量en和ecn的初始论域；u为输出变量un的初始论域；动态权值参数ρ称为带宽，取值为1左右；参数ε称为贴现因子，ε∈(0,1)；δ为充分小的正数。本申请的混合型伸缩因子相关参数值分别取：输入变量en和ecn的初始论域e、ec和输出变量un的初始论域u均定义为[-7,7]；ρ＝1，ε＝0.98，δ＝0.002。

运用上述设计的三关节机械臂变论域模糊控制系统进行轨迹跟踪控制仿真时，需要先获得控制系统的输入qdn，即三个关节的期望关节角度。

表4三关节机械臂的d-h参数

以三个关节均为旋转关节的机械臂为例，其d-h参数见表4。an连杆长度，αn两关节轴之间的夹角，dn关节偏置，θn关节转角。通常，对于转动关节，关节转角θn为关节变量，其他三个参数是固定不变的。

根据d-h参数选取如式(11)所示的笛卡尔空间轨迹，取弧长s为参数，可以建立如式(12)所示的弧长参数方程。

其中，x、y、z为标准笛卡尔空间的坐标系轴，一组(x，y，z)代表空间上点的位置坐标。

采用基于相平面的时间最优轨迹规划方法获得期望关节角度，作为三关节机械臂变论域模糊控制系统进行轨迹跟踪控制仿真时的输入qdn。以机械臂末端走完式(12)轨迹所花时间最短为优化目标，最终得出三关节机械臂各个关节的轨迹。由于所获得的三个关节的轨迹是无法显式表达的非线性函数，所以可根据得出的各个关节的轨迹获取时间-关节角度序列，选取0.02秒的时间间隔进行一次采样，则每一个采样时间对应输出机械臂的一组三个关节角度值，即为期望关节角度值，亦即为机械臂变论域模糊控制系统的输入qdn。如表5和图2所示。

表5三关节机械臂期望轨迹采样点值

运用matlab/simulink仿真环境搭建了三关节机械臂变论域模糊控制仿真系统。设置仿真步长t＝0.02秒，仿真总时长为0.4秒时，则机械臂各个关节均可获取21个采样时间-期望关节角度序列，因而亦可获得21个采样时间-笛卡尔空间轨迹点坐标序列，见表6。当设置仿真总时长为1.2秒时，可获得60个采样时间-笛卡尔空间轨迹点坐标序列，可以实现跟踪式(11)所表示的三关节机械臂笛卡尔空间轨迹的理想整圆。

为验证本申请所提出的基于比例-指数混合型伸缩因子的变论域模糊控制器的控制效果，运用两个实验进行了对比分析。

实验一是将本申请提出的比例-指数混合型伸缩因子与现有的文献(基于matlab的双关节机械手控制系统仿真研究，该文献同样讨论的是机械臂轨迹跟踪的变论域模糊控制问题)提出的指数型伸缩因子

的变论域模糊控制器分别应用于三关节机械臂关节角度轨迹跟踪控制仿真，得到如图2、图3、图4所示的关节角度输出响应曲线。图2是关节1分别使用混合型伸缩因子与指数型伸缩因子的变论域模糊控制器跟踪机械臂期望关节轨迹所获得的关节角度的对比图，图3、图4分别为关节2和关节3的关节角度的对比图。由图3、图4、图5可见，与文献基于指数型伸缩因子的变论域模糊控制器相比，使用本申请所设计的基于比例-指数混合型伸缩因子的变论域模糊控制器，机械臂各关节角度输出均无超调，响应速度更快。

实验二是对比分析了本申请提出的比例-指数混合型伸缩因子与现有文献提出的指数型伸缩因子的变论域模糊控制器分别应用于笛卡尔空间机械臂轨迹跟踪控制的误差。首先，将使用两种伸缩因子的变论域模糊控制器得到的60个机械臂末端轨迹点序列，分别运用最小二乘拟合法进行圆轨迹拟合，获得半径分别为0.598m和0.592m的圆，可见，相对于理想圆半径0.6m来说，本申请提出的混合型伸缩因子的变论域模糊控制方法拟合出的圆的半径误差较小。然后，以式(11)表示的理想圆上的轨迹点与仿真获得的轨迹点的欧几里得距离来表示轨迹跟踪误差，误差对比结果如图6所示，横坐标为采样点编号，纵坐标为误差值。表6列出了分别使用指数型伸缩因子和混合型伸缩因子的变论域模糊控制方法进行机械臂轨迹跟踪控制时，前21个采样点的笛卡尔空间轨迹跟踪误差值。由图6和表6可见，与基于指数型伸缩因子的变论域模糊控制方法相比，本申请所设计的基于混合型伸缩因子的变论域模糊控制系统具有更小的误差。

以上两个实验的结果表明，本申请提出的基于比例-指数混合型伸缩因子的变论域模糊控制方法，使得机械臂的关节空间和笛卡尔空间的轨迹跟踪控制均具有更好的控制效果。

表6笛卡尔空间轨迹误差值

本发明不局限于上述实施例,在本公开的技术方案的基础上,本领域的技术人员根据所公开的技术内容,不需要创造性的劳动就可以对其中的一些技术特征作出一些替换和变形,这些替换和变形均在本发明的保护范围内。