高超声速飞行器俯冲段制导、姿控、变形一体化控制方法与流程

本发明涉及飞行器控制领域，尤其涉及一种高超声速变形飞行器俯冲段制导控制方法。

背景技术：

变形飞行器能够根据飞行任务需求，对外形进行灵活改变，从而满足大空域和大速域的飞行要求，从而保持最优飞行，使得该飞行器能够完成常规飞行器不能完成的任务。变形飞行器作为新一代跨大气层飞行的空天飞行器，在速度、高度变化范围广泛的区域，达到良好作战使用性能。

高超声速变形飞行器是指能够根据飞行环境和飞行任务的需求，主动地改变外形结构，以获得更优的气动特性和操纵能力，可以满足大空域和大速域的飞行要求，有利于提高的飞行性能的一类高超声速飞行器。高超声速变形飞行器将外形参数作为可控变量，利用外形参数对气动特性的影响来改变飞行器的性能，使其能够适应更宽范围内的飞行空域和速域，从而能够适应更复杂的飞行任务和飞行环境。同时，通过针对战场环境、作战任务变化，灵活地改变外形结构、飞行性能等，增强了飞行器的射程、突防性和精确性，可以大幅提高飞行器的作战效能和效费比。

在俯冲段，对于高超声速乘波飞行器，偏离设计状态时气动性能急剧恶化，变形技术可有效解决这一问题。高超声速飞行器具有马赫数变化范围大和过载大等特点，质心运动和绕心运动均呈现出快时变、非线性、强耦合和不确定性等特点，传统的飞行器制导和控制系统主要是基于工程经验或奇异摄动理论对控制和制导子系统进行分离设计，没有利用控制和制导子系统之间的耦合信息，而一体化制导控制系统可以充分利用控制和制导子系统之间的耦合信息来改善整个系统的性能。目前该领域的研究主要针对高超声速固定外形飞行器的制导控制设计，以及变形飞行器的稳定控制问题，对于高超声速变形导弹的控制研究以及如何利用变形进行辅助飞行任务控制的成果较少。

技术实现要素：

针对现有技术中高超声速变形飞行器俯冲段的控制以及如何利用变形进行辅助飞行控制的问题，本发明的目的是提供一种高超声速变形飞行器俯冲段制导、姿控、变形一体化控制方法，通过对高超声速变形飞行器俯冲段进行制导、控制、变形的一体化设计，使得高超声速变形飞行器能够很好地实现俯冲段飞行的任务需求。

为了实现上述发明目的，本发明采用的技术方案是：

一种高超声速飞行器俯冲段制导、姿控、变形一体化控制方法，包括以下步骤：

基于高超声速变形飞行器的几何模型，构建其六自由度运动模型以及气动模型；

基于面向控制的高超声速变形飞行器相对于目标的运动方程、面向控制的高超声速变形飞行器绕质心运动学方程以及面向控制的高超声速变形飞行器绕质心运力学方程，构建高超声速变形飞行器俯冲段带落角约束的制导、姿态控制、变形一体化控制模型；

基于动态面方法设计高超声速变形飞行器俯冲段带落角约束的制导、姿态控制、变形一体化控制模型的控制方案；

将当前运动目标相对于高超声速变形飞行器质心的距离rt、运动目标的纬度经度λt作为高超声速变形飞行器俯冲段带落角约束的制导、姿态控制、变形一体化控制模型的输入，根据高超声速变形飞行器俯冲段带落角约束的制导、姿态控制、变形一体化控制模型的控制方案生成控制舵偏角及高超声速变形飞行器的变形率指令，并输入到超声速变形飞行器的六自由度运动模型，高超声速变形飞行器将跟踪运动目标，完成飞行任务。

本发明中，所述高超声速变形飞行器的六自由度运动模型如下：

式中：m为高超声速变形飞行器弹体的质量，a＝[avaθaσ]^t为高超声速变形飞行器弹体加速度在半速度坐标系中的投影,ω＝[ωxωyωz]为三轴旋转角速度；v为飞行速度，θ为速度倾角，σ为速度偏航角；gh＝[ghxghyghz]^t为引力加速度在半速度坐标系中的分量；ix、iy、iz为高超声速变形飞行器的三轴转动惯量。

l,d,n分别为高超声速变形飞行器所受到升力、阻力和侧力，其表达式分别为

分别为升力系数，阻力系数，侧力系数，q＝0.5ρv²为动压，ρ为大气密度，s0为高超声速变形飞行器未变形时的参考面积。

m＝[mxmymz]^t分别为高超声速变形飞行器所受到的滚转力矩、偏航力矩和俯仰力矩，其表达式为

b和c分别为高超声速变形飞行器横侧向参考长度和纵向参考长度，分别为高超声速变形飞行器的滚转力矩系数、偏航力矩系数和俯仰力矩系数。

fs′＝[f′sxf′syf′sz]^t的表达式如下：

hv和bv分别表示速度坐标系到半速度坐标系和体坐标系的转换矩阵，fsi为由于高超声速变形飞行器变形引起的附加力。

ms＝[msxmsymsz]^t为由于高超声速变形飞行器变形产生的附加力矩，其表达式如下：

mi为高超声速变形飞行器其弹翼质量，i＝1,2，g为地球引力矢量，vo为高超声速变形飞行器弹体质心速度矢量，si为高超声速变形飞行器弹翼的质心相对飞行器质心的位置矢量。

本发明中，高超声速变形飞行器的气动模型如下：

式中，分别为滚转力矩系数、偏航力矩系数，俯仰力矩系数，ξ为变形率、各个变量的结构如下：

βn＝[β],δyn＝[δy]

βmx＝[β],δxmx＝[δx]

βmy＝[β],δymy＝[δy]

其中，α为攻角、β为侧滑角、δx为滚转舵、δy为偏航舵、δz为俯仰舵，均为系数矩阵，为给定的设计参数，已知量，其中分别为αl、δxl、δzl、αd、δxd、δyd、δzd、βn、δyn、βmx、δxmx、βmy、δymy、αmz、δzmz的系数矩阵，同样为系数矩阵，各个其余变量均为各个系数矩阵。分别为αl、δxl、δzl、αd、δxd、δyd、δzd、βn、δyn、βmx、δxmx、βmy、δymy、αmz、δzmz的系数矩阵。

本发明中，面向控制的高超声速变形飞行器相对于目标的运动方程为：

式中：

γdf为终端时刻的速度倾角，λd为视线倾角，λt为视线偏角，rt为飞行器质心相对于目标点的距离，shi,ji,j＝1,2,3分别为半速度系到视线系的转换矩阵sh中的元素，i表示行，j表示列；视线系的原点为目标点o，oxs轴沿高超声速变形飞行器与目标连线，由目标指向高超声速变形飞行器，oys轴位于视线平面内且垂直于oys轴，ozt轴与其它两轴构成右手直角坐标系。

视线倾角λd和视线偏角λt由下式计算得到

xt、yt和zt分别为高超声速变形飞行器相对于目标地理坐标系的位置矢量在目标地理坐标系中的投影

tg为地面坐标系到目标地理坐标系的转换矩阵；tg的表达式如下：

tg＝m2[0.5π]m1[φt]m3[λt-0.5π][λ0-λ](m2[a0-0.5π]m1[φ0]m3[λ0-0.5π])

其中m1[·],m2[·],m3[·]依次表示绕x轴、y轴和z轴对应的初等转换矩阵，其具体形式分别为

λ0,φ0为出发点的经度和纬度，为已知量；

a0为发射方位角，其表达式为：

a0＝arcsin(cos(φt)sin(λt-λ0)/sin(a))

其中，a＝sin(φ0)sin(φt)+cos(φ0)cos(φt)cos(λt-λ0)；

x,y,z为高超声速变形飞行器在地面坐标系的位置坐标，x,y,z计算公式如下：

对视线倾角λd和视线偏角λt求导得到视线倾角变化率和视线偏角变化率分别为

式中，

vxt、vyt和vztvxtvytvzt是高超声速变形飞行器相对于地面的速度矢量在目标地理坐标系中的投影

所述面向控制的高超声速变形飞行器相对于目标的运动方程的输出xf为视线倾角λd与速度倾角γdf之和，输出x0为视线倾角λd以及视线偏角λt的变化率，输入为升力系数cl的两个分量。

本发明中，面向控制的高超声速变形飞行器绕质心运动学方程为：

式中，

通过面向控制的高超声速变形飞行器绕质心运动学方程求出x1＝[αβγv]^t，代入高超声速变形飞行器的气动模型，可求出升力系数进而可求得面向控制的高超声速变形飞行器相对于目标的运动方程的输入

所述面向控制的高超声速变形飞行器绕质心运动学方程其输入为高超声速变形飞行器的三轴旋转角速度矢量x2＝[ωxωyωz]^t。

本发明中，面向控制的高超声速变形飞行器绕质心运力学方程为：

式中

面向控制的高超声速变形飞行器绕质心运力学方程的输出即为x2，输入为高超声速变形飞行器的控制舵偏角u＝[δxδyδz]^t。

联立面向控制的高超声速变形飞行器相对于目标的运动方程、面向控制的高超声速变形飞行器绕质心运动学方程以及面向控制的高超声速变形飞行器绕质心运力学方程，即建立高超声速变形飞行器俯冲段带落角约束的制导、姿态控制、变形一体化控制模型。

本发明中，高超声速变形飞行器俯冲段带落角约束的制导、姿态控制、变形一体化控制模型的控制方案如下：

上述控制方案中：

s0为定义的第一个动态面，x01、x02为x0的分量，kf为角误差项系数，为给定的参数；x1d为第一个虚拟控制输入，k0＝diag(k01k02)为给定的正的增益常数；ε01和ε02为待给定的饱和函数项增益；d01和d02为给定的边界层厚度；sat(s,d)为饱和函数，其定义为：

f0′为落角约束项求导的结果：

γvd为所求的倾侧角指令值，cld为升力系数指令值，均通过x1d求解得到；αd为攻角的指令值，通过升力系数指令值求得；为升力系数关于攻角的导数矩阵；ξt-1表示上一个计算时刻的变形率，cl0,t-1，均为上一时刻的分量，为关于变形率ξ的导数；

s1为定义的第二个动态面，为x1与其指令值x1d的差值，x2d为第二个动态面的虚拟控制输入；k1＝diag(k11,k12,k13)为给定的正的增益常数；根据该虚拟控制量x2d得到使得x1达到预期期望指令值x1d的三通道角速率虚拟输入期望值ωxd,ωyd,ωzd；定义s2为第三个动态面，为x2与其指令值x2d的差值，u为第三个动态面的控制输入。k2＝diag(k21k22k23)为给定的正的增益常数，根据三通道角速率虚拟输入期望值x2d得到设计舵偏角输入u及变形输入ξ以完成对飞行器姿控系统的稳定控制和制导控制。

本发明还提供一种高超声速飞行器俯冲段制导、姿控、变形一体化控制系统，包括：

目标信息采集模块，用于采集当前运动目标相对于高超声速变形飞行器质心的距离rt、运动目标的纬度经度λt；

制导模块，接收目标信息采集模块采集到的目标信息，并输入到预先加载在该模块上的高超声速变形飞行器俯冲段带落角约束的制导、姿态控制、变形一体化控制模型，根据预先设计好的高超声速变形飞行器俯冲段带落角约束的制导、姿态控制、变形一体化控制模型的控制方案生成控制舵偏角及高超声速变形飞行器的变形率指令；

姿控-变形控制模块，接收制导模块生成的控制舵偏角及高超声速变形飞行器的变形率指令，并输入到预先加载在该模块上的超声速变形飞行器的六自由度运动模型中，完成高超声速变形飞行器的稳定运动以及实现对制导指令的跟踪控制。

本发明还提供一种高超声速变形飞行器，其采用的技术方案是：一种高超声速变形飞行器，包括机体与设在机体内的机载电路板，所述机载电路板上设有处理器与存储器，所述存储器存储有计算机程序，所述处理器执行所述计算机程序时实现上述高超声速变形飞行器俯冲段制导、姿控、变形一体化控制方法的步骤。

本发明还提供一种计算机可读存储介质，其上存储有计算机程序，其特征在于，所述计算机程序被处理器执行时实现上述高超声速飞行器俯冲段制导、姿控、变形一体化控制方法的步骤。

本发明的有益技术效果：

本发明针对高超声速变形飞行器在俯冲段飞行设计了制导控制系统。对变形飞行器的变形方式进行了设计，并对其建立气动模型，该气动模型包含了变形对气动的影响。在充分考虑机翼变形的情况下，建立了适用于倾斜转弯控制的俯冲段带落角约束的制导控制模型，并基于块动态面方法进行制导、姿态控制、变形的一体化方法设计，从而形成一套完整可用的高超声速变形飞行器俯冲段制导控制系统设计方法。该方法适用于高超声速变形飞行器俯冲段飞行任务的完成，工程应用意义重大，有效解决高超声速变形飞行器在俯冲段制导控制设计与变形控制的协调稳定问题，同时保证制导控制系统设计方法的鲁棒性，实现俯冲段的飞行任务需求，适用于高超声速变形飞行器俯冲段制导、姿态控制、变形一体化设计。

附图说明

图1是本实施例的流程示意图

图2是高超声速变形飞行器的几何模型图

图3是速度坐标系与半速度坐标系示意图

图4是体标系示意图

图5是地面标系示意图

图6是飞行器与目标的空间相对位置关系图

图7是俯冲段飞行中的三维轨迹曲线图

图8是俯冲段飞行中的飞行器在地面发射坐标系的坐标图

图9是俯冲段飞行中的高度、速度及当地速度倾角变化曲线图

图10是俯冲段飞行中的马赫数、动压及空气密度的变化曲线图

图11是俯冲段飞行中的攻角、侧滑角及倾侧角的变化曲线图

图12是俯冲段飞行中的滚转舵、偏航舵及升降舵的变化曲线图

图13是俯冲段飞行中的展长变形率的变化曲线图。

具体实施方式

为了便于本发明的实施，下面结合具体实例作进一步的说明。

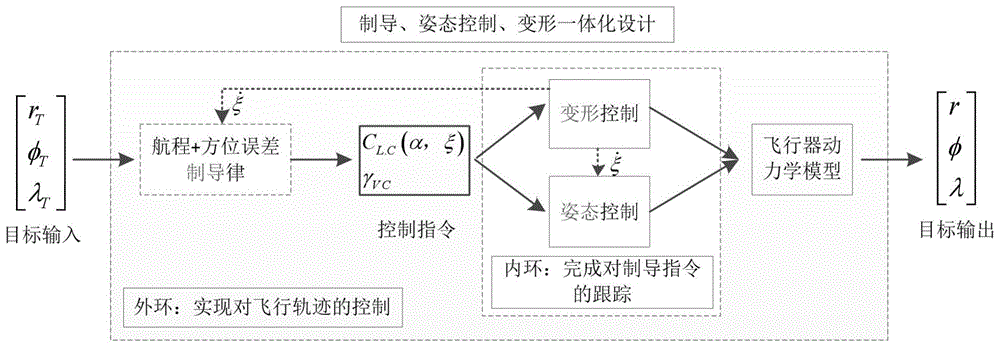
如图1所示的是本实施例的控制流程示意图，采集当前运动目标相对于高超声速变形飞行器质心的距离rt、运动目标的纬度经度λt，将(rt、λt)输入制导模块，外环回路为制导回路，对高超声速变形飞行器进行轨迹规划与控制，要求制导精度要高。制导模块接收目标信息采集模块采集到的目标信息，生成控制舵偏角及高超声速变形飞行器的变形率指令。内环回路为控制回路，要求实现高超声速变形飞行器的稳定运动以及实现对制导模块输出的制导指令的跟踪控制，要求精度以及鲁棒性要高。姿控-变形控制模块包括高超声速变形飞行器的变形控制与姿态控制两部分，通过高超声速变形飞行器变形与姿态变化协同完成对制导指令的控制，同时变形控制与姿态控制之间相互作用，保证飞行器在变形过程中的运动稳定及指令的稳定跟踪，从而运动至输入的运动目标。

本实施例中，高超声速飞行器俯冲段制导、姿控、变形一体化控制方法，包括以下步骤：

s1基于高超声速变形飞行器的几何模型，构建其六自由度运动模型以及气动模型。

其中高超声速变形飞行器的几何模型如图2所示，依此所建立的高超声速变形飞行器的六自由度运动模型如下：

式中：m为高超声速变形飞行器弹体的质量，a＝[avaθaσ]^t为高超声速变形飞行器弹体加速度在半速度坐标系中的投影,ω＝[ωxωyωz]为三轴旋转角速度。如图3所示，半速度坐标系的原点为高超声速变形飞行器的质心o，oxh轴沿高超声速变形飞行器速度方向，与速度坐标系的oxv轴重合，oyh位于过oxh的铅垂平面内且垂直于oxh轴，向上为正，ozh轴与其它两轴构成右手直角坐标系。v为飞行速度，θ为速度倾角，σ为速度偏航角。

gh＝[ghxghyghz]^t为引力加速度在半速度坐标系中的分量。ix、iy、iz为高超声速变形飞行器的三轴转动惯量。

l,d,n分别为高超声速变形飞行器所受到升力、阻力和侧力，具体表达式分别为

式中，分别为升力系数，阻力系数，侧力系数，q＝0.5ρv²为动压，ρ为大气密度，s0为高超声速变形飞行器未变形时的参考面积。

m＝[mxmymz]^t分别为高超声速变形飞行器所受到的滚转力矩、偏航力矩和俯仰力矩，具体表达式为

式中，b和c分别为高超声速变形飞行器横侧向参考长度和纵向参考长度，分别为高超声速变形飞行器的滚转力矩系数、偏航力矩系数和俯仰力矩系数。

fs′＝[f′sxf′syf′sz]^t的表达式如下：

式(4)中，hv和bv分别表示速度坐标系到半速度坐标系和体坐标系的转换矩阵，fsi为由于高超声速变形飞行器变形引起的附加力。

如图4所示，体坐标系的原点为高超声速变形飞行器的质心o，oxb轴指向高超声速变形飞行器头部，oyb轴位于高超声速变形飞行器纵向对称面内且与oxb轴垂直，向上为方，ozb轴与其它两轴构成右手直角坐标系。机体系oxb轴方向称为轴向，oyb轴方向称为法向，ozb轴方向称为侧向。如图3所示，速度坐标系的原点为高超声速变形飞行器的质心o，oxv轴沿高超声速变形飞行器速度方向，oyv轴位于高超声速变形飞行器纵向对称面内且与oxv轴垂直，向上为方，ozv轴与其它两轴构成右手直角坐标系。

式中，ms＝[msxmsymsz]^t为由于高超声速变形飞行器变形产生的附加力矩，其表达式如下：

式(5)中，mi为高超声速变形飞行器其弹翼质量，i＝1,2，g为地球引力矢量，vo为高超声速变形飞行器弹体质心速度矢量，si为高超声速变形飞行器弹翼的质心相对飞行器质心的位置矢量。

高超声速变形飞行器的气动模型如下：

式(6)中，分别为滚转力矩系数、偏航力矩系数，俯仰力矩系数，ξ为变形率、各个变量的结构如下：

其中，α为攻角、β为侧滑角、δx为滚转舵、δy为偏航舵、δz为俯仰舵，其余变量均为各个系数矩阵，均为已知量。

s2：基于面向控制的高超声速变形飞行器相对于目标的运动方程、面向控制的高超声速变形飞行器绕质心运动学方程以及面向控制的高超声速变形飞行器绕质心运力学方程，构建高超声速变形飞行器俯冲段带落角约束的制导、姿态控制、变形一体化控制模型。

由图6所示，视线倾角λd和视线偏角λt可以由下式计算得到

式中，xt、yt和zt分别为高超声速变形飞行器相对于目标地理坐标系的位置矢量在目标地理坐标系中的投影

其中式中tg为地面坐标系到目标地理坐标系的转换矩阵,其表达式为：

tg＝m2[0.5π]m1[φt]m3[λt-0.5π][λ0-λ](m2[a0-0.5π]m1[φ0]m3[λ0-0.5π])

其中m1[·],m2[·],m3[·]依次表示绕x轴、y轴和z轴对应的初等转换矩阵，其具体形式为

λ0,φ0为出发点的经度和纬度，为已知量。a0为发射方位角，其表达式为：

a0＝arcsin(cos(φt)sin(λt-λ0)/sin(a))

其中，a＝sin(φ0)sin(φt)+cos(φ0)cos(φt)cos(λt-λ0)。

x,y,z为高超声速变形飞行器在地面坐标系的位置坐标，如图5所示，地面坐标系的原点o0为初始时刻高超声速变形飞行器的地心矢径与标准地球椭球体表面的交点，o0ya轴沿地心矢径方向且向上为正，o0xa轴指向射向方向且垂直于o0ya轴，o0za轴与其它两轴构成右手直角坐标系。地面坐标系与地球表面固连在一起，随地球一同转动，如图6所示，目标地理坐标系的原点为目标点o，oyt轴沿飞行器地心矢径方向且向上为正，oxt轴位于过原点o的子午面内且垂直于oyt轴，指向北极为正，ozt轴与其它两轴构成右手直角坐标系。

x,y,z计算公式如下：

对式(8)求导得到视线倾角变化率和视线偏角变化率分别为

式中，

vxt、vyt和vztvxtvytvzt是高超声速变形飞行器相对于地面的速度矢量在目标地理坐标系中的投影。

tg从而可得面向控制的高超声速变形飞行器相对于目标的运动方程为：

式(14)中，

式(15)中，如图6所示，γdf为终端时刻的速度倾角,λd为视线倾角，λt为视线偏角，rt为飞行器质心相对于目标点的距离，shi,ji,j＝1,2,3分别为半速度系到视线系的转换矩阵sh中的元素，i表示行，j表示列。如图6所示，视线系的原点为目标点o，oxs轴沿飞行器与目标连线，由目标指向飞行器，oys轴位于视线平面内且垂直于oys轴，ozt轴与其它两轴构成右手直角坐标系。

上述带落角约束的面向控制的高超声速变形飞行器相对于目标的运动模型的输出xf为视线倾角λd与速度倾角γdf之和，输出x0为视线倾角λd以及视线偏角λt的变化率，输入为升力系数cl的两个分量，而输入则需要从面向控制的高超声速变形飞行器绕质心运动学方程求取。

以攻角α，侧滑角β，倾侧角γv表示面向控制的高超声速变形飞行器绕质心运动学方程为：

式(16)中，

通过高超声速变形飞行器绕质心运动学方程，可以求出x1＝[αβγv]^t，代入高超声速变形飞行器的气动模型即式(6)，可求出升力系数进而可求得式(14)的输入由此式(16)及式(14)的输入输出关系即可确定。

对于式(16)，其输入为高超声速变形飞行器的三轴旋转角速度矢量x2＝[ωxωyωz]^t，该输入可由面向控制的高超声速变形飞行器绕质心运力学方程求得。

面向控制的高超声速变形飞行器绕质心运力学方程如下：

式(18)中

该高超声速变形飞行器面向控制的绕质心动力学方程的输出即为x2，输入为高超声速变形飞行器的控制舵偏角u＝[δxδyδz]^t。由此式(18)及式(16)的输入输出关系即可确定。

通过联立面向控制的高超声速变形飞行器相对于目标的运动方程、面向控制的高超声速变形飞行器绕质心运动学方程以及面向控制的高超声速变形飞行器绕质心运力学方程，即联立(14)、式(16)和式(18)，即可建立高超声速变形飞行器俯冲段带落角约束的制导、姿态控制、变形一体化控制模型如下：

s3.基于动态面方法设计高超声速变形飞行器俯冲段带落角约束的制导、姿态控制、变形一体化控制模型的控制方案；

上述控制方案中，

控制方案中，s0为定义的第一个动态面，x01、x02为x0的分量，kf为角误差项系数，为给定的参数。x1d为第一个虚拟控制输入，k0＝diag(k01k02)为待给定的正的增益常数；ε01和ε02为待给定的饱和函数项增益；d01和d02为待给定的边界层厚度。sat(s,d)为饱和函数，其定义为：

f0′为落角约束项求导的结果：

γvd为所求的倾侧角指令值，cld为升力系数指令值，均通过x1d求解得到。αd为攻角的指令值，通过升力系数指令值求得。为升力系数关于攻角的导数矩阵，其与变形率ξ有关。ξt-1表示上一个计算时刻的变形率，cl0,t-1，均为上一时刻的分量，为关于变形率ξ的导数。

以上便是由制导系统动力学方程(14)和制导系统被控状态变量期望变化规律设计与姿控系统相关的虚拟控制量α,γv以及变形率ξ的过程。

s1为定义的第二个动态面，为x1与其指令值x1d的差值，x2d为第二个动态面的虚拟控制输入；k1＝diag(k11,k12,k13)为给定的正的增益常数。根据该虚拟控制量x2d得到使得x1达到预期期望指令值x1d的三通道角速率虚拟输入期望值ωxd,ωyd,ωzd；

最后定义s2为第三个动态面，为x2与其指令值x2d的差值，u为第三个动态面的控制输入。k2＝diag(k21k22k23)为给定的正的增益常数，根据三通道角速率虚拟输入期望值x2d可以得到设计舵偏角输入u及变形输入ξ以完成对飞行器姿控系统的稳定控制和制导控制。

s4.将当前运动目标相对于高超声速变形飞行器质心的距离rt、运动目标的纬度经度λt作为高超声速变形飞行器俯冲段带落角约束的制导、姿态控制、变形一体化控制模型的输入，根据高超声速变形飞行器俯冲段带落角约束的制导、姿态控制、变形一体化控制模型的控制方案生成控制舵偏角及高超声速变形飞行器的变形率指令，并输入到超声速变形飞行器的六自由度运动模型，高超声速变形飞行器将跟踪运动目标，完成飞行任务。

下面基于建立的高超声速飞行器俯冲段制导、姿控、变形一体化控制系统进行仿真验证：

仿真算例：

为了验证高超声速飞行器俯冲段制导、姿控、变形一体化控制方法的有效性，对模型进行数值仿真。高超声速飞行器制导控制一体化设计的方法效果、初始状态及一体化模型参数表如下表1、表2所示。

表1飞行器的俯冲初始状态和目标点的经纬度

表2一体化设计方法参数优化值

二、结果分析

仿真结果如图7-图13所示。

从图7可知，采用块动态面的制导控制一体化设计方法下的下压段飞行弹道是先缓慢上升再快速下降的，且飞行器可以从出发点飞行至目标点，同时尽可能满足落角约束的。由图8可知，飞行器的落点脱靶量为73.27m，飞行时间为64.2s。由图9可知，飞行器落点速度为2174m/s，落地速度倾角为60.44°，符合落角约束的控制需求。由图10可知，飞行过程中，由于速度减小，飞行器马赫数逐渐减小，落地时马赫数大小为6.45；由于高度降低，大气密度逐渐增大，飞行器的动压则在速度和大气密度的共同作用下，呈现出先缓慢增加后急剧增加的变化，在落地时动压大小为2718kpa。由图11可知，在俯冲段初始时刻，攻角急剧增加，此时下压升力最大，使飞行器的速度倾角方向下偏，进入下压状态，然后变化缓慢，末端攻角为3.23°。由于采用btt控制，侧滑角的全程变化也十分微小，倾侧角初始值为0°，然后经历了一次翻转达到了180°，产生向下升力使得飞行器下压。由图12可知，滚转舵和偏航偏角基本维持在0°左右，在倾侧角翻转时经历了一次调整。飞行器升降舵偏角在初始调整阶段变化较为剧烈，在下压状态稳定之后，保持十分缓慢的增加。图13展现了变展长飞行器在俯冲段全程的展长变化，在初始段展长变化较为剧烈，之后展长变化较为平缓，展长和攻角的组合变化完成和制导任务所需的升力变化。

为了更好地实现飞行器在俯冲段的飞行任务，本发明基于块动态面的方法设计了高超声速变形飞行器俯冲段带落角约束的制导、姿态控制、变形一体化控制模型的控制方案，利用飞行器的变形特性对升力进行控制，发挥了变形辅助飞行器机动的作用，提高了飞行器的任务适应能力验证了方法在俯冲段的有效性，有效解决高超声速变形飞行器制导、控制、变形之间协调困难的问题。

以上所述实施例仅表达了本申请的几种实施方式，其描述较为具体和详细，但并不能因此而理解为对发明专利范围的限制。应当指出的是，对于本领域的普通技术人员来说，在不脱离本申请构思的前提下，还可以做出若干变形和改进，这些都属于本申请的保护范围。因此，本申请专利的保护范围应以所附权利要求为准。