可重复使用运载器全阶段再入返回制导方法与流程

本发明属于航空航天飞行器制导领域，特别是涉及一种可重复使用运载器全阶段再入返回制导方法。

背景技术：

可重复使用运载器(rlv，reusablelaunchvehicle)是指能够自由往返于地球与空间轨道之间执行载荷运送任务的多用途可重复使用飞行器。rlv全阶段再入返回过程从120千米开始，到地面结束，整个再入返回过程飞行包线大，高度跨越太空域，亚轨道和航空域，速度跨越高超声速，超声速和亚声速。单一的再入返回制导方法无法在如此复杂的飞行环境下完成安全返回着陆任务，因此一般将再入返回过程分为三个阶段：再入段(120km-25km)、终端能量管理段(25km-3km)和自动着陆段(3km-地面)。

在再入段，rlv需要在具有极大初始再入动能和势能的条件下，经历高超声速向亚声速的过渡，需要严格满足再入过程的热流约束、动压约束和过载约束，是保证rlv实现安全稳定再入飞行较为关键的一段。根据飞行特点，再入段又可以分为初始下降段(120km-80km)和下滑段(80km-25km)。在初始下降段，大气密度稀薄，rlv不满足拟平衡滑翔条件，需要设计倾侧角指令，使得rlv能进入拟平衡滑翔条件；在下滑段，rlv跨越大气层，在严格满足各种约束的同时，实现能量耗散，最终精确地进入终端能量管理段初始窗口。

在终端能量管理段，rlv需要耗散再入段结束后rlv所具有的能量，同时调整航向使其对准跑道，保证rlv能够以合适的高度、速度、位置、航向等状态约束条件进入预定的着陆窗口，终端能量管理段区别于另外两个飞行阶段的主要特征是存在航向校正锥来进行航向校正，通过将航天器与航向校正锥相切，设计倾侧角指令，实现能量的耗散并调整航向使rlv对准跑道。

自动着陆段是再入返回飞行过程的最后阶段，它的完成标志着整个再入返回飞行过程的圆满结束，该段主要追求的目标是rlv能够以合理的速度、位置和下沉率在指定的跑道位置安全可靠地着陆。

目前，针对rlv全阶段再入返回制导问题，国内外的学者都只是针对再入返回阶段中的某一阶段进行制导律设计而缺乏全阶段再入返回制导方法，导致存在模型及气动参数不统一，多段之间切换点处存在状态量跳变等问题。因此，针对上述问题，本发明对于全阶段再入返回制导律进行了设计，在统一的运动学模型和气动参数下，分别设计了再入段、终端能量管理段及自动着陆段的制导方法并设置了各个段之间的切换条件，使rlv能克服外界扰动不确定性从而实现实现120千米到地面的rlv全阶段再入返回。

技术实现要素：

为克服现有技术的不足，本发明旨在提出一种rlv全阶段再入返回制导方法，使得rlv从120km开始，在受到外界扰动和不确定因素影响的情况下，仍能够获得使轨迹严格满足热流、过载及动压约束的制导指令，最终以恰当的速度在指定的跑道位置着陆。为此，本发明采取的技术方案是，可重复使用运载器全阶段再入返回制导方法，步骤如下：

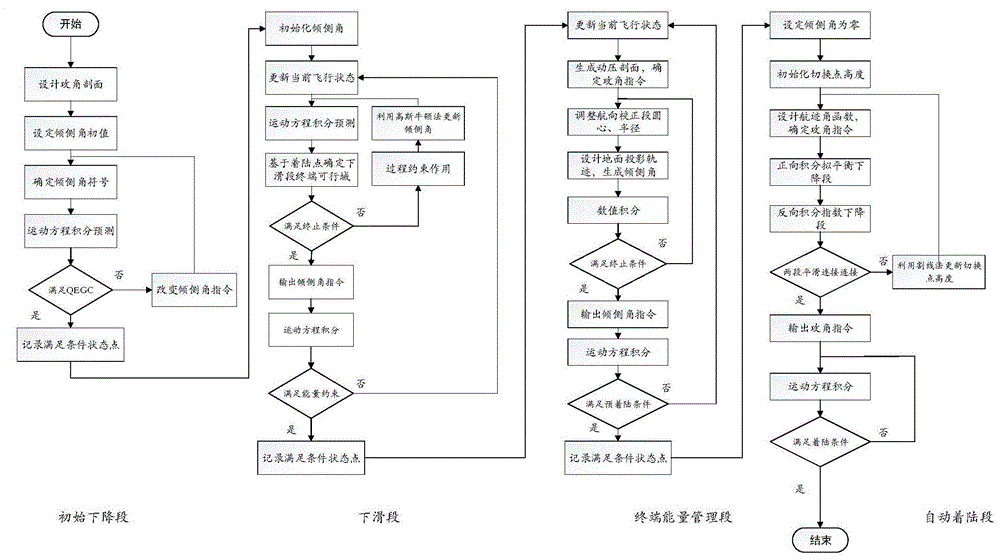
第一部分，初始下降段制导：设计固定的倾侧角指令，使可重复使用运载器rlv能够进入拟平衡滑翔条件，并以rlv进入拟平衡滑翔条件状态点作为下滑段初始状态点；

第二部分：下滑段制导：考虑下滑段过程约束以及终端约束，通过设计攻角-速度剖面及基于终点预测偏差的倾侧角校正方法，完成约束条件下的三维预测校正制导律设计，以rlv积分至下滑段终端能量处实际状态点作为终端能量管理段初始状态点；

第三部分：终端能量管理段制导：分开考虑纵向及横向制导律，在纵向上，设计动压-高度剖面以保持动压较小的变化率，并基于动力学方程确定动压与攻角的对应关系；在横向上，基于地面航线轨迹，设计航向角进而确定倾侧角指令，使rlv能够对准跑道，以rlv积分至终端能量管理段末端高度处实际状态点作为自动着陆段初始状态点；

第四部分：自动着陆段制导：在横向上，保持倾侧角为0；在纵向上，自动着陆段设计为由拟平衡下滑段和指数下滑段组合而成，通过设计航迹角函数确定攻角指令，并通过割线法设计两段切换点处的高度，使rlv能够以预定的速度及航迹角触地。

具体实现过程如下：

第一步：在rlv再入返回过程，假设飞行器为无动力飞行的质点，考虑地球为旋转椭球时，忽略再入过程中侧力以及地球自转的影响，并取侧滑角为零，建立统一的rlv再入三自由度运动方程为：

式中中飞行状态r,θ,φ,ν,γ,χ分别表示地心距、经度、纬度、飞行速度、航迹角和航向角，σ表示倾侧角，m表示飞行器质量。重力加速度g＝μg/r²，升力l，阻力d表示式如下：

式中：s表示rlv气动参考面积，动压qd＝0.5ρν²，大气密度其中ρ0为海平面处的大气密度，re为地球半径，β为常值系数，升力系数cl和阻力系数cd表示为攻角α和气动参数的函数；

综合考虑到热防护系统以及可操作性需求，在初始下降段及下滑段中，攻角设计为关于速度的剖面

第二步：在初始下降段，通过积分预测，对rlv是否进入拟平衡滑翔条件qegc进行判定，采用计算量较小的递增策略设计制导指令，由动力学方程式(33)得到

此外，在式(33)中的第五项中假设航迹角γ满足cosγ≈1和得到拟平衡滑翔条件：

进而得到满足拟平衡滑翔条件的

由式(37)和式(39)，建立是否满足拟平衡滑翔条件判定如式(40)，从而确定是否由初始下降段过渡到再入段

式中δ>0为常数。初始下降段的制导方法则通过设计倾侧角幅值，取初次迭代σini＝0°，倾侧角符号则由航向角和视线角之间的关系得到

sign(σini)＝-sign(χ-χsight)(9)

式中χsight为视线角；

与此同时，攻角指令则可由式(36)得到。在上述倾侧角和攻角的作用下，对式(33)进行积分预测，并对式(40)进行判定，若存在满足条件的状态点则结束初始下降段；否则令σini＝σini+5°，由式(41)确定符号后重新进行积分预测以及判定，直到满足拟平衡下降条件；

第三步：在下滑段，考虑初始下降段的终端状态作为下滑段的初始状态约束，路径约束包括热流密度约束、动压约束和过载约束如式(42)，以及下滑段终端状态约束通过对下滑段终点的积分预测以及基于落点偏差的校正策略，设计制导指令：

路径约束式：

式中：kq为与飞行器相关的常数，qmax，nmax分别是最大允许的热流、动压和过载，由于时间不是下滑段决定性参数，无法通过约束终端时间从而确定积分预测范围，需要采用一个新的微分量，由于高度在下滑段不是一个单调的变量，无法选取为微分量；若选取速度为微分量，则在运动方程的分母中引入了一项可能等于0的项-d/m-gsinγ，因此，引入下述形式的能量变量作为独立变量：

能量变量e是一个单调递增的变量；此外，它体现了高度与速度的关系，可在运动方程中省去关于速度的表达式，增加了积分预测的速度；

由式(43)和运动方程式(33)可以得到代入到式(33)中得到以能量为微分量的运动方程：

考虑运动方程式(44)，设计制导方法时，攻角指令由式(36)给出，因此只需要设计侧倾角的制导指令σgliding，采用预测校正的方法对其进行设计；

在预测环节中，在每个制导周期内，给定初始倾侧角σgliding⁽⁰⁾，其符号由航向角和视线角之间的关系得到，并考虑式(44)对能量变量e进行积分，得到下滑段终点处的预测终点经纬度(θgf,φgf)；

在校正环节中，设置性能指标函数为

j＝j0(σ0)+kc(σ0)(13)

式中：表示当前倾侧角指令作用下终端预测经纬度与指定终端经纬度点的偏差；k为惩罚因子，表示在再入过程中对路径约束的违反，为基于着陆点反向求解的下滑段终端经纬度状态点，反向求解过程的制导指令在后续步骤中给出；

基于所给出的性能指标函数式(45)，采用如式(46)的高斯牛顿法对倾侧角进行迭代求解：

式中λi为当次迭代使性能指标函数值减小的最小自然数；

上述迭代求解目的为寻求倾侧角指令σgliding⁽ⁱ⁾，使满足式(47)

j(σgliding)≤δ(15)

式中δ为反向求解过程中，考虑着陆时速度和沿航迹方向的地面轨迹存在一定的余量所求得的可行范围。在每个制导周期内，重复上述对于倾侧角的迭代求解步骤，得到满足条件的倾侧角并对式(44)进行积分，最终得到下滑段终点处的终端状态

第四步：在终端能量管理段，考虑下滑段的终端状态作为终端能量管理段的初始状态，分别从纵向上和横向上对制导指令进行设计；在终端能量管理段中，高度h＝r-re为一个单调递减的变量，因此选取高度代替时间作为微分量，由于需要考虑地面投影轨迹变化情况，在运动方程中以rlv在地面坐标系中的位置(y,x)代替经纬度(θ，φ)，得到以高度为微分量的运动方程：

在纵向上，为了避免动压以较大的速率变化，设计动压关于高度的多项式

qd(h)＝q0+q1h+q2h²+q3h³(17)

式中h为海拔高度，h＝r-re，多项式系数q0,q1,q2,q3由下列条件得到：

1)终端能量管理段起始点的高度rt0＝rgf与动压

2)终端能量管理段与自动着陆段接口处高度高度hali与动压

3)终端能量管理段与自动着陆段接口处为了保持拟平衡滑翔条件，

4)taem段高度中点hmid处的动压满足

基于高度-动压剖面qd(h)，在制导过程中，根据相应高度即可得到对应的动压值。由qd＝0.5ρν²，及动力学方程式(33)，得到

由式(49)可得到

联立式(50)及式(51)，可得到阻力系数cd关于高度的函数，

联立式(35)与式(52)，可求得相应的攻角指令，完成纵向制导；

在横向上，通过设计rlv地面投影轨迹来设计航向角的变化规律，进而确定倾侧角指令，根据地面投影轨迹的不同，侧向制导可分为4个部分，捕获段、直线飞行段、航向校正段和预着陆段：

1)在捕获段中，rlv调整航向角以对准校正圆柱相切点，倾侧角指令

式中，rac为捕获段设计转弯半径。

2)在直线飞行段中，rlv保持航向角不变，倾侧角指令

σ＝0(22)

3)在航向校正段中，rlv绕校正圆柱飞行以消耗能量以及对准跑道，倾侧角指令

式中，rhac为校正圆柱半径。

4)在最终段中，rlv保持航向角不变，切换至自动着陆段，倾侧角指令

σ＝0(24)

结合纵向的攻角指令与横向的倾侧角制导，得到rlv终端能量管理段制导指令，对式(48)进行积分，最终得到终端能量管理终点处的终端状态hali为终端能量管理段关于高度的终点；

第五步：在自动着陆段，考虑终端能量管理段的终端状态作为自动着陆段的初始状态，设计倾侧角指令σlanding保持为0，即不考虑rlv的横向飞行，仅在纵向平面内设计攻角指令使得rlv在着陆场处满足安全降落条件；

自动着陆段制导方法设计可概述为：设计攻角指令αlanding使得rlv在既定地面处满足安全降落条件。具体实现可分为两段：拟平衡下降段及指数下降段。在拟平衡下降段中，rlv保持拟平衡滑翔条件通过设计攻角指令使航迹角γ保持不变；在指数下降段中，按指数变化规律设计航迹角，航迹角逐渐减小到降落航迹角γtd，与此同时，rlv高度逐渐减小直到接触降落跑道。

在指数下降段中，由可推导出

式中，γ0表示自动着陆段起始点处的航迹角，由式(34)和式(35)，可以得到拟平衡下降段的攻角指令

式中l由式(57)给出，在指数下降段中中，设计航迹角的变化趋势

tanγ＝tanγtde^-ks(27)

式中：k在下面给出，s表示在x方向上以着陆点处的s＝0为基准，与着陆点之间的距离，在自动着陆过程中是一个负数；γtd为预设的触地航迹角；

由式(48)，可推得代入式(59)并积分得到

通过条件：s＝0处h＝0，推导出考虑拟平衡下降段和指数下降段连接点处的(hf,sf)，由式(59)和式(60)有

由式(48)和式(60)得到

则可推导出

将式(64)代入到式(58)中，得到指数下降段的攻角指令αgliding2；

如此自动着陆段的制导问题转变为寻求拟平衡下降段与指数下降段的切换点hf，使两段可以平滑的切换，采用高斯牛顿法对hf进行求解，将性能指标设置为两段积分之间s的误差δs，最终得到使δs＝0的hf，进而确定两段的攻角指令，完成自动着陆段的制导，实现rlv的安全着陆。

本发明的特点及有益效果是：

本发明设计了一种rlv全阶段再入返回制导方法，使得rlv能够在制导指令作用下，生成严格满足约束的飞行轨迹，最终以恰当的速度在指定的跑道位置着陆。由于本发明所涉及的制导方法不依赖于标称轨迹而是根据rlv当前状态设计制导指令，所以对外界干扰具备良好的鲁棒性。此外，不同于传统方法对再入返回进行分段并对每一段赋予初值及约束条件，本发明实现了对再入返回各个段之间的整合以及模型统一，消除了传统方法中由于各个段分开求解所产生状态量的跳变。最终本发明通过构建rlv再入返回虚拟仿真系统对所提出的制导方法的有效性及鲁棒性进行了验证。

附图说明：

附图1rlv全阶段再入返回制导方法流程图。

附图2正常飞行状态下高度变化曲线。

附图3正常飞行状态下经度变化曲线。

附图4正常飞行状态下纬度变化曲线。

附图5正常飞行状态下速度变化曲线。

附图6正常飞行状态下航迹角变化曲线。

附图7正常飞行状态下航向角变化曲线。

附图8两种情况下rlv全阶段再入返回三维轨迹。

附图9两种情况下高度-速度变化曲线。

具体实施方式

本发明以预测校正制导为主要研究手段，发明了一种可重复使用运载器全阶段再入返回制导方法并通过matlab软件进行虚拟仿真实验，验证了本方法的有效性。本发明步骤如下：

第一部分，初始下降段制导方法设计：考虑到rlv在再入返回初期120km处空气较为稀薄，且rlv不满足拟平衡滑翔条件，设计固定的倾侧角指令，使rlv能够进入拟平衡滑翔条件，并以rlv进入拟平衡滑翔条件状态点作为下滑段初始状态点。

第二部分：下滑段制导方法设计：考虑下滑段过程约束以及终端约束，通过设计攻角-速度剖面及基于终点预测偏差的倾侧角校正方法，完成约束条件下的三维预测校正制导律设计。以rlv积分至下滑段终端能量处实际状态点作为终端能量管理段初始状态点。

第三部分：终端能量管理段制导方法设计：分开考虑纵向及横向制导律，在纵向上，设计动压-高度剖面以保持动压较小的变化率，并基于动力学方程确定动压与攻角的对应关系；在横向上，基于地面航线轨迹，设计航向角进而确定倾侧角指令，使rlv能够对准跑道。以rlv积分至终端能量管理段末端高度处实际状态点作为自动着陆段初始状态点。

第四部分：自动着陆段制导方法设计：在横向上，保持倾侧角为0；在纵向上，自动着陆段设计为由拟平衡下滑段和指数下滑段组合而成，通过设计航迹角函数确定攻角指令，并通过割线法设计两段切换点处的高度。使rlv能够以预定的速度及航迹角触地。

具体实现过程如下：

第一步：在rlv再入返回过程，假设飞行器为无动力飞行的质点，考虑地球为旋转椭球时，忽略再入过程中侧力以及地球自转的影响，并取侧滑角为零。建立统一的rlv再入三自由度运动方程为

式中中飞行状态r,θ,φ,ν,γ,χ分别表示地心距、经度、纬度、飞行速度、航迹角和航向角。σ表示倾侧角，m表示飞行器质量。重力加速度g＝μg/r²，升力l，阻力d表示式如下：

式中：s表示rlv气动参考面积，动压qd＝0.5ρν²，大气密度其中ρ0为海平面处的大气密度，re为地球半径，β为常值系数，升力系数cl和阻力系数cd表示为攻角α和气动参数的函数。

综合考虑到热防护系统以及可操作性需求，在初始下降段及下滑段中，攻角设计为关于速度的剖面

第二步：在初始下降段，通过积分预测，对rlv是否进入拟平衡滑翔条件(qegc)进行判定，采用计算量较小的递增策略设计制导指令。由动力学方程式(33)可得到

此外，在式(33)中的第五项中假设航迹角γ满足cosγ≈1和可得到拟平衡滑翔条件

进而得到满足拟平衡滑翔条件的

由式(37)和式(39)，建立是否满足拟平衡滑翔条件判定如式(40)，从而确定是否由初始下降段过渡到再入段

式中δ>0为常数。初始下降段的制导方法则通过设计倾侧角幅值，取初次迭代σini＝0°，倾侧角符号则由航向角和视线角之间的关系得到

sign(σini)＝-sign(χ-χsight)(41)

式中χsight为视线角。

与此同时，攻角指令则可由式(36)得到。在上述倾侧角和攻角的作用下，对式(33)进行积分预测，并对式(40)进行判定，若存在满足条件的状态点则结束初始下降段；否则令σini＝σini+5°，由式(41)确定符号后重新进行积分预测以及判定，直到满足拟平衡下降条件。

第三步：在下滑段，考虑初始下降段的终端状态作为下滑段的初始状态约束，路径约束包括热流密度约束、动压约束和过载约束如式(42)，以及下滑段终端状态约束通过对下滑段终点的积分预测以及基于落点偏差的校正策略，设计制导指令。

路径约束式：

式中：kq为与飞行器相关的常数，qmax，nmax分别是最大允许的热流、动压和过载。由于时间不是下滑段决定性参数，无法通过约束终端时间从而确定积分预测范围，需要采用一个新的微分量。由于高度在下滑段不是一个单调的变量，无法选取为微分量；若选取速度为微分量，则在运动方程的分母中引入了一项可能等于0的项-d/m-gsinγ。因此，引入下述形式的能量变量作为独立变量

能量变量e是一个单调递增的变量；此外，它体现了高度与速度的关系，可以在运动方程中省去关于速度的表达式，增加了积分预测的速度。

由式(43)和运动方程式(33)可以得到代入到式(33)中可得到以能量为微分量的运动方程：

考虑运动方程式(44)，设计制导方法时，攻角指令由式(36)给出，因此只需要设计侧倾角的制导指令σgliding，采用预测校正的方法对其进行设计。

在预测环节中，在每个制导周期内，给定初始倾侧角σgliding⁽⁰⁾，其符号由航向角和视线角之间的关系得到，并考虑式(44)对能量变量e进行积分，得到下滑段终点处的预测终点经纬度(θgf,φgf)。

在校正环节中，设置性能指标函数为

j＝j0(σ0)+kc(σ0)(45)

式中：表示当前倾侧角指令作用下终端预测经纬度与指定终端经纬度点的偏差；k为惩罚因子，表示在再入过程中对路径约束的违反。为基于着陆点反向求解的下滑段终端经纬度状态点，反向求解过程的制导指令在后续步骤中给出。

基于所给出的性能指标函数式(45)，采用如式(46)的高斯牛顿法对倾侧角进行迭代求解：

式中λi为当次迭代使性能指标函数值减小的最小自然数。

上述迭代求解目的为寻求倾侧角指令σgliding⁽ⁱ⁾，使满足式(47)

j(σgliding)≤δ(47)

式中δ为反向求解过程中，考虑着陆时速度和沿航迹方向的地面轨迹存在一定的余量所求得的可行范围。在每个制导周期内，重复上述对于倾侧角的迭代求解步骤，得到满足条件的倾侧角并对式(44)进行积分，最终得到下滑段终点处的终端状态

第四步：在终端能量管理段，考虑下滑段的终端状态作为终端能量管理段的初始状态，分别从纵向上和横向上对制导指令进行设计。

在终端能量管理段中，高度h＝r-re为一个单调递减的变量，因此可行选取高度代替时间作为微分量。此外，由于需要考虑地面投影轨迹变化情况，在运动方程中以rlv在地面坐标系中的位置(y,x)代替经纬度(θ，φ)，得到以高度为微分量的运动方程

在纵向上，为了避免动压以较大的速率变化，设计动压关于高度的多项式

qd(h)＝q0+q1h+q2h²+q3h³(49)

式中h为海拔高度，h＝r-re。多项式系数q0,q1,q2,q3由下列条件得到：

5)终端能量管理段起始点的高度rt0＝rgf与动压

6)终端能量管理段与自动着陆段接口处高度高度hali与动压

7)终端能量管理段与自动着陆段接口处为了保持拟平衡滑翔条件，

8)taem段高度中点hmid处的动压满足

基于高度-动压剖面qd(h)，在制导过程中，根据相应高度即可得到对应的动压值。由qd＝0.5ρν²，及动力学方程式(33)，可得到

由式(49)可得到

联立式(50)及式(51)，可得到阻力系数cd关于高度的函数，

联立式(35)与式(52)，可求得相应的攻角指令，完成纵向制导。

在横向上，通过设计rlv地面投影轨迹来设计航向角的变化规律，进而确定倾侧角指令，根据地面投影轨迹的不同，侧向制导可分为4个部分，捕获段、直线飞行段、航向校正段和预着陆段：

5)在捕获段中，rlv调整航向角以对准校正圆柱相切点，倾侧角指令

式中，rac为捕获段设计转弯半径。

6)在直线飞行段中，rlv保持航向角不变，倾侧角指令

σ＝0(54)

7)在航向校正段中，rlv绕校正圆柱飞行以消耗能量以及对准跑道，倾侧角指令

式中，rhac为校正圆柱半径。

8)在最终段中，rlv保持航向角不变，切换至自动着陆段，倾侧角指令

σ＝0(56)

上述4个部分给出了完整的横向制导指令。结合纵向的攻角指令与横向的倾侧角制导，得到rlv终端能量管理段制导指令，对式(48)进行积分，最终得到终端能量管理终点处的终端状态hali为终端能量管理段关于高度的终点。

第五步：在自动着陆段，考虑终端能量管理段的终端状态作为自动着陆段的初始状态，设计倾侧角指令σlanding保持为0，即不考虑rlv的横向飞行，仅在纵向平面内设计攻角指令使得rlv在着陆场处满足安全降落条件。

自动着陆段制导方法设计可概述为：设计攻角指令αlanding使得rlv在既定地面处满足安全降落条件。具体实现可分为两段：拟平衡下降段及指数下降段。在拟平衡下降段中，rlv保持拟平衡滑翔条件通过设计攻角指令使航迹角γ保持不变；在指数下降段中，按指数变化规律设计航迹角，航迹角逐渐减小到降落航迹角γtd，与此同时，rlv高度逐渐减小直到接触降落跑道。

在指数下降段中，由可推导出

式中，γ0表示自动着陆段起始点处的航迹角，由式(34)和式(35)，可以得到拟平衡下降段的攻角指令

式中l由式(57)给出，在指数下降段中中，设计航迹角的变化趋势

tanγ＝tanγtde^-ks(59)

式中：k在下面给出，s表示在x方向上以着陆点处的s＝0为基准，与着陆点之间的距离，在自动着陆过程中是一个负数；γtd为预设的触地航迹角。

由式(48)，可推得代入式(59)并积分可得到

通过条件：s＝0处h＝0，可推导出考虑拟平衡下降段和指数下降段连接点处的(hf,sf)，由式(59)和式(60)有

由式(48)和式(60)可以得到

则可推导出

将式(64)代入到式(58)中，可得到指数下降段的攻角指令αgliding2。

如此自动着陆段的制导问题转变为寻求拟平衡下降段与指数下降段的切换点hf，使两段可以平滑的切换。采用高斯牛顿法对hf进行求解，将性能指标设置为两段积分之间s的误差δs，最终得到使δs＝0的hf，进而确定两段的攻角指令，完成自动着陆段的制导，实现rlv的安全着陆。

结合附图对本发明作进一步详述。

在虚拟仿真环境下，仿真参数设定如下：rlv的基础参数与再入约束参数如表1所示，升力系数cl＝-0.2070+1.6756α，阻力系数cd＝0.0785-0.3529α+2.0400α²。

表1飞行器再入参数

分两种情况进行仿真测试验证，第一种情况考虑正常飞行状态下的rlv再入返回制导，验证本发明所提出制导方法的有效性；第二种情况考虑外界扰动下的rlv再入返回制导，验证本发明所提出制导方法的鲁棒性。

第一种情况的给定指令为：高度从120000km变化到0km、速度从7600m/s变化到200m/s、经度从0rad变化到1.15rad、纬度从0rad变化到0.47rad。图2-图7给出了正常飞行状态下，各状态量相对于能量的变化曲线。由于时间不是全阶段返回的指标之一，因此采取能量作为自变量能更好的体现各状态量的变化情况。从图中可以看出，在正常飞行状态下，本发明提出的制导方法可以有效可靠的引导rlv飞向预期落点。

第二种情况给定指令未变，但是在下滑段初期给rlv加入外部扰动：高度偏差dr＝1000m，速度偏差dν＝100m/s。图8给出了正常飞行状态下和外界扰动情况下，rlv全阶段再入返回三维轨迹图；图9给出了正常飞行状态下和外界扰动情况下，rlv的高度-速度变化曲线。从图8和图9中可以看出，本发明提出的制导方法在rlv受到外界扰动的情况下仍能引导rlv飞向预期落点，具备良好的鲁棒性。