一种非规则形状移动机器人的路径规划方法与流程
本发明属于移动机器人路径规划技术领域,具体涉及一种非规则形状移动机器人的路径规划方法。
背景技术:
路径规划是移动机器人研究领域的一个核心问题,它的目标就是在工作环境中寻找一条连接机器人当前状态和目标状态的行使路线,并且避免与环境中的障碍物发生碰撞。目前,路径规划的研究方法包括细胞分解法、人工势场法以及各类智能算法等,但这些方法主要是针对单点机器人,即将机器人视为形状规则的单个元素,以机器人的尺寸对工作空间进行网络划分,在此基础上进行路径规划,路径规划算法中只考虑机器人的2自由度移动。实际情况下,大多数机器人的形状是非规则的,非规则形状机器人的路径规划不仅需要考虑2自由度移动,还需要考虑其转动,例如,在某些复杂环境下,受到障碍物的影响,机器人只能作移动运动或在一定角度范围内转动,这些是路径规划中的重要约束。其次,工作空间中的障碍物有可能比机器人的尺寸要小,现在的解决办法是将障碍物形状进行拓展,即划分的工作空间网格内只要有障碍物,就将整个网格均视为障碍物,这就造成可能的行使路径被忽略了,即所谓的“pathblocked”问题。此外,路径规划中,还需要考虑机器人行使的安全性,避免“tooclose”或者“toofar”问题。
技术实现要素:
针对上述技术问题,本发明提出了一种非规则形状移动机器人的路径规划方法,本发明是将生物神经网络和卷积神经网络相融合,可以控制路径安全性的规划方法,以解决复杂环境下、非规则形状移动机器人的路径规划难题。该方法将机器人的工作空间均匀划分成拓扑网络结构,并进行生物神经动力学迭代计算,采用迭代计算稳定后的网络节点函数值描述工作空间的环境信息;根据移动机器人的形状特征构成核矩阵,将核矩阵与工作空间的生物神经网络进行卷积计算,获得机器人在网络节点的移动状态矩阵和转动状态矩阵;以机器人在工作空间初始节点位置和方向为初始条件,逐步迭代搜索,构建从初始状态到目标状态的节点树,最后反向搜索节点树,获得机器人的规划路径。
路径规划中,机器人和目标均包括x、y坐标和方向θ三维状态参数,考虑了机器人的2自由度移动和1自由度转动运动,并且可以通过调节卷积计算中的安全系数因子,控制规划路径与障碍物之间的距离,调节机器人行使路径的安全性。
本发明的技术方案是:一种非规则形状移动机器人的路径规划方法,包括以下步骤:
构建工作空间网络:将机器人的二维工作空间均匀划分成拓扑的工作空间网络t,并对工作空间网络t进行生物神经动力学迭代计算,构成工作空间的生物神经网络s,生物神经网络s描述了整个工作空间的环境信息;
构建机器人形状核矩阵:根据移动机器人的形状特征构成核矩阵;
构建机器人的移动状态矩阵和转动状态矩阵:将核矩阵与工作空间的生物神经网络进行卷积计算,获得机器人在网络节点的移动状态矩阵和转动状态矩阵;
构建节点树tree:以机器人在工作空间初始位置和方向为初始条件,逐步迭代搜索,构建从初始状态到目标状态的节点树tree;
生成规划路径:反向搜索节点树tree,获得机器人的规划路径。
上述方案中,所述构建工作空间网络的步骤具体为:
将机器人的二维工作空间均匀划分成拓扑的工作空间网络t,工作空间网络t的每个节点包括自由空间和障碍物占据两个状态,自由空间的节点函数值设定为0,障碍物占据的节点函数值设定为1,工作空间网络t中的节点ti会与周边8个节点相邻,将工作空间网络t进行生物神经动力学迭代计算,构成工作空间的生物神经网络s,生物神经网络s上节点的函数值描述了该节点所在位置的环境信息,生物神经网络s则描述了整个工作空间的环境信息。
上述方案中,所述生物神经网络s迭代计算公式为:
公式一中,xi为第i个神经元节点si的在t时刻的函数值,a、b、d为设定的非负恒定参数,且有a>b>d,ii为生物神经网络节点si的外界激励,且有
上述方案中,所述构建机器人形状核矩阵步骤具体为:
将移动机器人所占据区域扩展成规则矩形或正方形区域,并进行均匀划分,构成核矩阵w,矩阵的每个元素包括自由空间和机器人占据两个状态,自由空间的元素值设定为0,机器人占据的元素值设定为1,将机器人在工作空间内,间隔45°进行旋转,构建反映机器人8个方向的核矩阵wθ,θ=1,2,...,8。
进一步的,所述构建机器人的移动状态矩阵和转动状态矩阵的步骤具体为:
将8组反映机器人形状的核矩阵wθ分别与生物神经网络s进行卷积计算,得到8个一层卷积网络h1,θ,h1,θ网络中每个节点的输出h1,θ(x,y)表示机器人是否能够以θ方向放置于工作空间节点(x,y),且h1,θ(x,y)=0表示能够放置,h1,θ(x,y)=-1表示不能够放置;
构建8个3×3的核矩阵mθ,用mθ分别对一层卷积网络h1,θ进行二次卷积计算,得到8个二层卷积网络h2,θ,h2,θ网络中每个节点的输出h2,θ(x,y)表示机器人是否能够以θ方向从当前节点(x,y)行使进入相邻的节点,且h2,θ(x,y)=0表示能够行驶进入,h2,θ(x,y)=-1表示不能够行驶进入;
提取h2,θ(x,y),θ=1,2,...,8,构成一个1×8的移动状态矩阵tsm(x,y),描述了机器人在当前节点的移动输出状态,即是否能够从节点(x,y)行使进入相邻的8个节点的状态;
提取h1,θ(x,y),θ=1,2,...,8,构成一个1×8的转动状态矩阵rsm(x,y),它由‘0’或‘-1’组成,描述机器人在节点(x,y)的转动状态。
进一步的,所述第一层卷积计算方法为:
公式二中,s为核矩阵wθ所在生物神经网络s中所占据的子空间集合,‘*’代表卷积计算,b表示安全系数,采用符号激活函数f(·),定义为
上述方案中,所述构建节点树的步骤具体为:
以机器人的初始状态,搜索机器人能够进入的相邻神经元信息,构成一组节点信息集合pstep,搜索步长step=step+1,判断目标信息是否属于信息集合pstep,如果目标信息属于信息集合pstep,则停止搜索,如果目标信息不属于信息集合pstep,则更新已经搜索的节点树tree,并将节点信息集合pstep设定为当前状态,进行下一步搜索,直到搜索到目标信息为止;
由每一步长的节点集合pstep,step=1,2,...p,构成一个从初始状态到目标状态的节点树tree。
上述方案中,所述生成规划路径具体步骤为:
根据所述节点树tree,输入机器人的初始位置(x0,y0)和方向θ0,输入目标位置(xp,yp)和方向θp;
从目标信息节点出发,搜索与之相连的父节点,构成父节点集合,确定路径节点,更新路径节点path,然后进行循环搜索,直到步长step=1,由每一步长step=1,2,...p搜索到的节点构成连接目标位置和初始位置的路径节点path,即规划路径。
进一步的,所述确定路径节点的确定具体为:如果父节点集合中有水平或垂直相连的父节点,则将其作为机器人行走路径节点,如果没有,则寻找与机器人当前方向转动角度较小的父节点,并将其作为机器人行走路径节点。
上述方案中,所述生物神经网络s的节点所描述的实际空间与反映机器人形状的核矩阵wθ的节点所描述的实际空间相等,机器人放置于生物神经网络s中所占据的是一个与核矩阵w大小相等的子网络,将反映机器人形状的核矩阵wθ放置于生物神经网络s中,能够保证wθ与s的节点位置一一对应。
与现有技术相比,本发明的有益效果是:本发明将生物神经网络和卷积神经网络融入路径规划中,提出一种非规则形状移动机器人的路径规划方法,通过构建核矩阵描述机器人的形状特征,用于任意非规则形状的移动机器人在复杂工作空间下的安全路径规划;由于工作空间划分网络的尺寸远小于机器人的尺寸,可以很好的描述小障碍物特征,解决密集散点障碍工作环境下“pathblocked”难题;只需要改变卷积计算中安全系数,就可实现规划路径与障碍物的距离的调节,方便地控制规划路径的安全性。
附图说明
图1是本发明一实施方式的机器人的工作空间划分示意图。
图2是本发明一实施方式的工作空间神经元节点连接示意图。
图3是本发明一实施方式的工作空间的生物神经网络构建示意图。
图4是本发明一实施方式的机器人形状核矩阵构建示意图。
图5是本发明一实施方式的卷积神经网络计算示意图。
图6是本发明一实施方式的二次卷积计算核矩阵示意图。
图7是本发明一实施方式的节点树的构建流程图。
图8是本发明一实施方式的生成规划路径的流程图。
图9是本发明一实施方式的在u型障碍工作环境下的规划路径图。
图10是本发明一实施方式的在密集散点障碍工作环境下的规划路径图。
具体实施方式
下面详细描述本发明的实施例,所述实施例的示例在附图中示出,其中自始至终相同或类似的标号表示相同或类似的元件或具有相同或类似功能的元件。下面通过参考附图描述的实施例是示例性的,旨在用于解释本发明,而不能理解为对本发明的限制。
一种非规则形状移动机器人的路径规划方法,包括以下步骤:
构建工作空间网络:将机器人的二维工作空间均匀划分成拓扑的工作空间网络t,并对工作空间网络t进行生物神经动力学迭代计算,构成工作空间的生物神经网络s,生物神经网络s描述了整个工作空间的环境信息;
构建机器人形状核矩阵:根据移动机器人的形状特征构成核矩阵;
构建机器人的移动状态矩阵和转动状态矩阵:将核矩阵与工作空间的生物神经网络进行卷积计算,获得机器人在网络节点的移动状态矩阵和转动状态矩阵;
构建节点树tree:以机器人在工作空间初始位置和方向为初始条件,逐步迭代搜索,构建从初始状态到目标状态的节点树tree;
生成规划路径:最后反向搜索节点树tree,获得机器人的规划路径。
所述构建工作空间网络的步骤具体为:
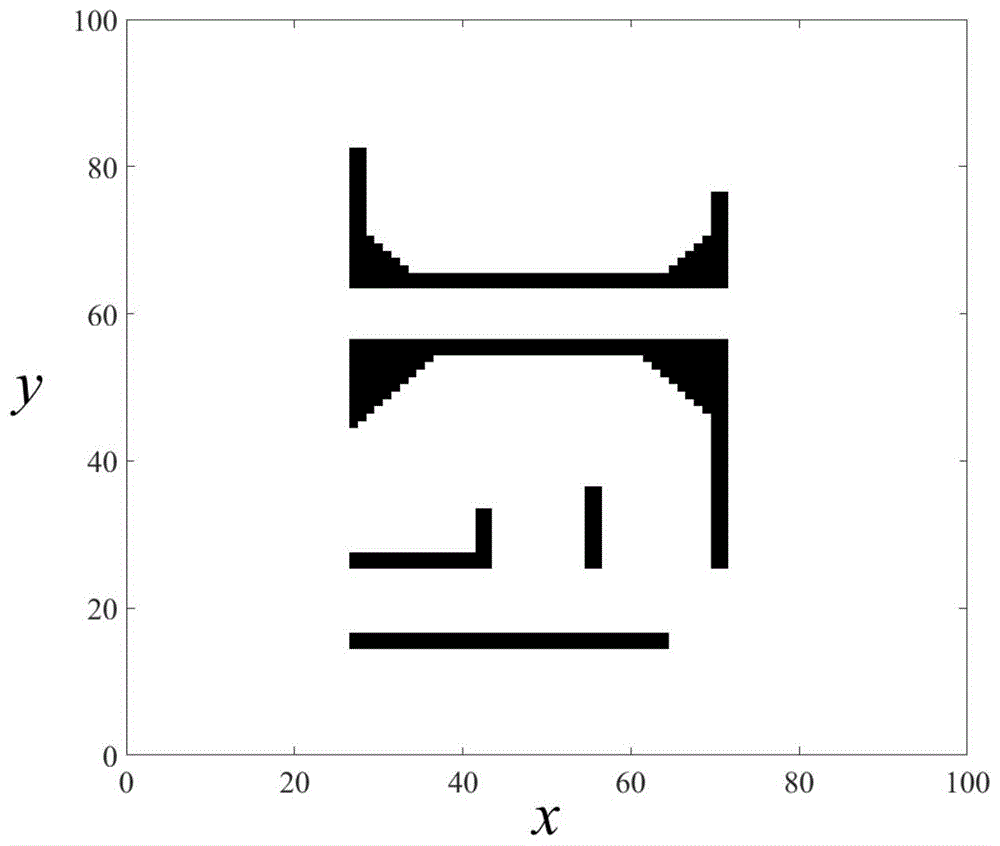
如图1所示,将移动机器人的二维工作空间沿x和y方向均匀划分成拓扑的工作空间网络t,图1中划分成100×100的网络结构,工作空间网络t的每个节点t(x,y)包括自由空间和障碍物占据两个状态,自由空间如图1中白色区域所示,自由空间的节点函数值设定为t(x,y)=0,障碍物占据如图1中黑色区域所示,障碍物占据的节点函数值设定为t(x,y)=1。
如图2所示,工作空间网络t中的节点ti的坐标为(x,y),节点ti会与周边8个节点相邻tj,j=1,2,...,8。
将工作空间网络t进行生物神经动力学迭代计算,构成工作空间的生物神经网络s,计算公式为
公式一中,xi为第i个神经元节点si的在t时刻的函数值,a、b、d为设定的非负恒定参数,且有a>b>d,ii为生物神经网络节点si的外界激励,且有
当设定参数a=10、b=1、d=0、e=50时,迭代计算稳定后得到的工作空间生物神经网络s如图3所示。
生物神经网络s上节点的函数值描述了该节点所在位置的环境信息,生物神经网络s则描述了整个工作空间的环境信息。
所述构建机器人形状核矩阵的步骤具体为:
移动机器人的形状可以是任意的;
假设为“箭头”形状移动机器人,将移动机器人所占据区域扩展成规则的矩形或正方形区域,并进行均匀划分,构成核矩阵w,图4中划分为9×9的正方形矩阵,矩阵的每个元素w(m,n)包括自由空间和机器人占据两个状态,自由空间的元素值设定为w(m,n)=0,机器人占据的元素值设定为w(m,n)=1。
将机器人在工作空间内,间隔45°进行旋转,构建反映机器人8个方向的核矩阵wθ,θ表示机器人前进方向,θ=1,2,...,8,如图4所示。
构建的生物神经网络s的节点所描述的实际空间应该与机器人形状核矩阵wθ的节点所描述的实际空间相等。
机器人放置于生物神经网络s中所占据的是一个与核矩阵w大小相等的子网络。
将机器人形状核矩阵wθ放置于生物神经网络s中,能够保证wθ与s的节点位置一一对应。
所述构建机器人的移动状态矩阵和转动状态矩阵的步骤具体为:
卷积神经网络计算结构参阅图5,构建的核矩阵参阅图6。
卷积神经网络计算结构如图5所示,将8组反映机器人形状的核矩阵wθ分别与生物神经网络s进行卷积计算,得到8个一层卷积网络h1,θ,卷积计算方法为
公式中,s为核矩阵wθ所在生物神经网络s中所占据的子空间集合,sp,q为s的子空间,‘*’代表卷积计算,b表示安全系数,采用符号激活函数f(·),定
卷积计算后,h1,θ网络中每个节点的输出h1,θ(x,y)表示机器人是否能够以θ方向放置于工作空间节点(x,y),且h1,θ(x,y)=0表示能够放置,h1,θ(x,y)=-1表示不能够放置。
如图6所示,构建8个3×3的核矩阵mθ,θ=1,2,…,8。
用mθ分别对一层卷积网络h1,θ进行二次卷积计算,得到8个二层卷积网络h2,θ,卷积计算中安全系数b设定为0。
二次卷积h2,θ网络中每个节点的输出h2,θ(x,y)表示机器人是否能够以θ方向从当前节点(x,y)行使进入相邻的节点,且h2,θ(x,y)=0表示能够行驶进入,h2,θ(x,y)=-1表示不能够行驶进入。
提取h2,θ(x,y),θ=1,2,...,8,构成一个1×8的移动状态矩阵tsm(x,y),它由‘0’或‘-1’组成,描述了机器人在当前节点的移动输出状态,即是否能够从节点(x,y)行使进入相邻的8个节点的状态。
例如,tsm(x,y)=[0,-1,-1,0,0,0,-1,0],表示机器人可以从节点(x,y)行使进入相邻5个节点(x+1,y)、(x+1,y-1)、(x,y-1)、(x-1,y-1)和(x-1,y+1)。
提取h1,θ(x,y),θ=1,2,...,8,构成一个1×8的转动状态矩阵rsm(x,y),它由‘0’或‘-1’组成,描述机器人在节点(x,y)的转动状态。
例如,rsm(x,y)=[-1,-1,-1,0,0,0,-1,0],表示机器人在节点(i,j)位置,可以在θ=4,5,和6范围内转动。
所述构建节点树的步骤具体为:
如图7所示,首先进行参数初始化:构建机器人工作空间信息,构建工作空间网络t;根据移动机器人的形状构建8个核矩阵wθ;输入机器人的初始位置(x0,y0)和方向θ0,输入目标位置(xp,yp)和方向θp;设定规划路径的安全系数b;步长step=0。
其次,根据工作空间网络t计算工作空间的生物神经网络s;通过卷积计算,获得生物神经网络s上机器人在每个节点的移动状态矩阵tsm和转动状态矩阵rsm。
然后,进入循环搜索程序。
以机器人的初始状态,搜索机器人能够进入的相邻神经元信息,构成一组节点信息集合pstep,搜索步长step=step+1;
判断目标信息是否属于信息集合pstep,如果目标信息属于信息集合pstep,则停止搜索;如果目标信息不属于信息集合pstep,则更新已经搜索的节点树tree,并将节点信息集合pstep设定为当前状态,进行下一步搜索,直到搜索到目标信息为止。
节点信息集合pstep包括机器人的位置和方向,只有当它们与目标位置(xp,yp)和方向θp均相等时,才说明机器人到达目标。
由每一步长的节点集合pstep,step=1,2,...p,构成一个从初始状态到目标状态的节点树tree。
搜索完成后,程序返回构建的搜索节点树tree。
所述生成规划路径具体步骤为:
如图8所示:首先,输入已经建立的搜索树tree,输入机器人的初始位置(x0,y0)和方向θ0,输入目标位置(xp,yp)和方向θp;步长step=step-1;
其次,从目标信息节点出发,搜索与之相连的父节点,构成父节点集合;如果父节点集合中有水平或垂直相连的父节点,则将其作为机器人行走路径节点,如果没有,则寻找与机器人当前方向转动角度较小的父节点,并将其作为机器人行走路径节点。
将上一步确定的路径节点作为当前节点,更新路径节点path,然后进行循环搜索,直到步长step=1。
由每一步长step=1,2,...p搜索到的节点增加到路径节点path,即逐步更新规划路径path。
程序返回连接目标位置和初始位置的路径节点path,即规划路径。
节点树tree的构建过程中,只需要通过设定第一层卷积计算中的安全系数b,可以控制路径与障碍物之间的距离,且随着b的增大,路径与障碍物之间的距离随之增加,以保证机器人行使的安全性。
规划得到的路径是在一定安全系数b情况下的最短路径。
u型障碍工作环境下的规划路径:
如图9所示,图9中箭头为前进方向,非规则形状移动机器人的路径规划考虑了机器人在工作空间内的3自由度运动,即2自由度平移和1自由度转动,机器人需要同时满足到达目标位置(xp,yp)和方向θp,才能生成路径。
可以通过设定安全系数b,改变所规划的路径,图9中,b3>b2>b1,可见随着安全系数的增大,所规划的路径也会随之作改变,规划的路径与障碍物的距离随之增大,以保证机器人运动的安全性。
密集散点障碍工作环境下的规划路:
如图10所示,本发明中,构建的生物神经网络s的节点所描述的实际空间与机器人形状的核矩阵wθ的节点所描述的实际空间相等,机器人在s中是占据一个子网络,且wθ与s的节点位置一一对应。这就使得生物神经网络s的节点所描述的实际空间要远小于机器人的尺寸,它可以更好的描述小障碍环境,图10给出了在密集散点障碍工作环境下的规划路径结果,通过设定安全系数b,b2>b1,也可以调节路径与障碍物的距离。
可见本发明是用于任意非规则形状的移动机器人在复杂工作空间下的安全路径规划,将机器人的工作空间均匀划分成拓扑网络结构,并进行生物神经动力学迭代计算,采用迭代计算稳定后的网络节点函数值描述工作空间的环境信息;根据移动机器人的形状特征构成核矩阵,将核矩阵与工作空间的生物神经网络进行卷积计算,获得机器人在网络节点的移动状态矩阵和转动状态矩阵;以机器人在工作空间初始位置和方向为初始条件,逐步迭代搜索,构建从初始状态到目标状态的节点树,最后反向搜索节点树,获得机器人的规划路径。该方法中,机器人可以是任意非规则形状,考虑了机器人的在平面空间的3自由度运动,并且在卷积计算中增加安全系数因子,控制规划路径与障碍物之间的距离,解决密集散点障碍工作环境下“pathblocked”难题;只需要改变卷积计算中安全系数,就可实现规划路径与障碍物的距离的调节,方便地控制规划路径的安全性。
上文所列出的一系列的详细说明仅仅是针对本发明的可行性实施例的具体说明,它们并非用以限制本发明的保护范围,凡未脱离本发明技艺精神所作的等效实施例或变更均应包含在本发明的保护范围之内。
- 还没有人留言评论。精彩留言会获得点赞!