一种基于3D打印喷头的粒子群模糊Smith温度控制方法与流程

本发明属于温度控制领域，具体涉及一种基于3d打印喷头的粒子群模糊smith温度控制方法。
背景技术：
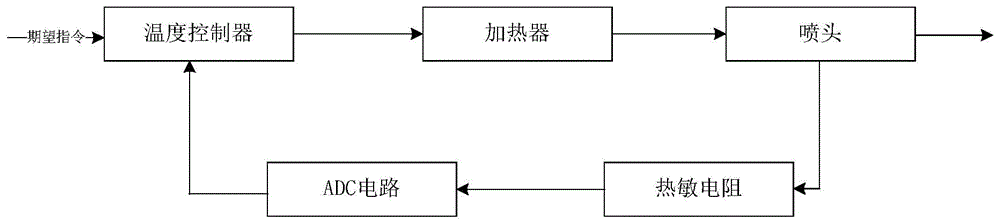
：对于3d打印机温度的控制，目前主流的方式还是通过pid方式进行调节。pid方式在很大一部分程度上可以满足一般的打印需求，但是当需要打印的物体精度要求更高时，可能会在一定程度上无法满足对精度的需求。这是因为打印机喷嘴的温度变化率较高，可以在很短的时间能上升几十度，反应度很高。通过常规的pid调节，在打印速度不高的情况下，可以大致上满足需求。但是当打印速度加快时，对温度控制产生的误差就会较大，温度过低时会影响到耗材的流通性和黏合性；温度过高又会在一定程度上之前熔化己经固化的耗材，发生一定的形变，影响成型的精度，对于含能材料3d打印领域，由于含能材料对于温度较为敏感，温度精度直接影响了含能材料打印的成型效果。现有的温度控制方法存在如下问题：(1)3d打印机喷头温度控制系统，由于传统pid算法由于参数值固定，存在着超调量过大，稳态时间过长等问题；(2)在模糊控制中，由于比例因子与量化因子固定，但系统干扰较多，需寻得其最优解；(3)3d打印机喷头温控系统采用电加热方式，具有很大时延性，延迟环节会使系统稳定性降低。技术实现要素：本发明的目的在于提供一种基于3d打印喷头的粒子群模糊smith温度控制方法。实现本发明目的的技术解决方案为：一种基于3d打印喷头的粒子群模糊smith温度控制方法，包括以下步骤：步骤(1)：采用atmega2560-16aupwm+gp8101产生可变直流电压，根据系统辨识结果设计模糊pid控制模型；步骤(2)：建立smith算法模型，得出系统由延时所差生的误差；步骤(3)：建立粒子群算法程序，得出比例因子和量化因子最优值；步骤(4)：将上述步骤中所设计的模糊pid算法、smith算法、粒子群算法结合起来，建立整体控制模型，从而实现对3d打印喷头的温度控制。进一步的，所述步骤(4)具体为：在模糊pid模型中将比例因子以及量化因子设为es、ecs和ps、is、ds，在粒子群程序中将输出量也设为es、ecs和ps、is、ds，粒子群算法的输出就成为了模糊pid的输入，同时将模糊pid模型中适应度函数中所需要的量引出作为粒子群算法的输入，这样模糊pid就与粒子群算法结合了起来；最后将smith算法得到的误差引入到总误差中，完成了整个模型的建立。进一步的，所述步骤(1)具体为：使用atmega2560-16au模拟口产生周期可变的pwm波，将其接入gp8101芯片，产生可变直流电压，将此电压接入加热棒中，使用不同的直流电压进行系统辨识；温度控制系统近似为一阶惯性延时系统，其传递函数表现为：式中：s-复频率设计模糊pid控制模型还需要确定输入输出模糊论域、比例因子、模糊子集和隶属度函数、模糊规则、去模糊方法以及量化因子。进一步的，所述输入输出模糊论域具体为：以误差e、误差变化率ec为输入，以δkp、δki、δkd为输出，误差及误差变化率的模糊论域范围为[-3,3]，δkp、δki、δkd模糊论域的范围为[-3,3]；所述模糊子集和隶属度函数：将模糊论域划分为七个模糊子集，对每一个模糊子集的范围以及隶属度函数详解如下：误差(e)：模糊论域范围为[-3,3]，划分为七个模糊子集{nb,nm,ns,zo,ps,pm,pb}，各模糊子集对应的隶属度函数及其定义域如下表所示：误差变化率(ec)：模糊论域范围为[-3,3]，划分为七个模糊子集{nb,nm,ns,zo,ps,pm,pb}，其隶属度函数以及定义域如下表所示：nbgaussmf[0.4248-3]nmtrimf[-3-2-1]nstrimf[-2-10]zogaussmf[0.12740]pstrimf[012]pmtrimf[123]pbgaussmf[0.42542.921]δkp：模糊论域范围为[-3,3]，划分为七个模糊子集{nb,nm,ns,zo,ps,pm,pb}，其隶属度函数以及定义域如下表所示：nbgaussmf[0.4248-3]nmtrimf[-3-1.999-1]nstrimf[-1.999-10]zotrimf[-101]pstrimf[012]pmtrimf[123]pbgaussmf[0.42543]δki：模糊论域范围为[-3,3]，划分为七个模糊子集{nb,nm,ns,zo,ps,pm,pb}，其隶属度函数以及定义域如下表所示：δkd：模糊论域范围为[-3,3]，划分为七个模糊子集{nb,nm,ns,zo,ps,pm,pb}，其隶属度函数以及定义域如下表所示：nbgaussmf[0.4248-3]nmtrimf[-3-1.998-1.002]nstrimf[-1.998-1.0020]zotrimf[-1.00201.002]pstrimf[01.0021.998]pmtrimf[1.0021.9983]pbgaussmf[0.42543]所述模糊规则的形式为：ifxisaandyisb,thenzisc，其中x,y为输入量，z为输出量，a,b为输入模糊量，c为输出模糊量；所述去模糊方法：采用面积重心法，面积重心法是取隶属度函数曲线与横坐标围成面积的重心，作为模糊推理的最终输出值，公式如下：式中：μ(v)-隶属度函数，v-变量值；所述比例因子和量化因子由粒子群算法程序输出。进一步的，所属步骤(2)建立smith算法模型，得出系统由延时所差生的误差，具体如下：将期望值与实际输出值之差作为误差一，将延时所产生的误差记为误差二，将误差一与误差二之差记为总误差，以此就建立出了smith算法模型。进一步的，步骤3所述建立粒子群算法程序，得出比例因子和量化因子最优值，具体过程如下：步骤(3-1)：初始化：设定参数的运动范围，设定学习因子c1、c2，最大进化代数g，kg表示当前的进化代数；在一个5维参数的搜索解空间中，粒子组成的种群规模大小为size，每个粒子代表解空间的一个候选解，其中第i(1≤i≤size)个粒子在整个解空间的位置表示为xi，速度表示为vi，第i个粒子从初始到当前迭代次数搜索产生的最优解为个体极值fgbest，整个种群目前的最优解为fzbest，随机产生初始种群的位置矩阵和速度矩阵；步骤(3-2)：适应度评价：将各个粒子初始位置作为个体极值，采用适应度函数：f(x)＝∫(t*|e(t)|)dt式中，t-时间，e(t)-误差，计算群体中各个粒子的初始适应值f(xi)，并求出种群最优位置；步骤(3-3)：更新粒子的速度和位置，产生新种群，并对粒子的速度和位置进行越界检查，为避免算法陷入局部最优，加入一个局部自适应变异算子进行调整，更新公式如下：其中，kg＝1,2,……,g，i＝1,2,……,size，r1和r2为0到1的随机数，c1为局部学习因子，c2为全局学习因子；步骤(3-4)：比较粒子的当前适应值f(xi)和自身历史最优值fgbesti，如果f(xi)优于fgbesti，则置fgbesti为当前f(xi)，并更新粒子位置；步骤(3-5)：比较粒子的当前适应值f(xi)和种群最优值fzbest，如果f(xi)优于fzbest，则置fzbest为当前f(xi)，并更新种群全局最优值；步骤(3-6)：检查结束条件，若满足，则结束寻优；否则kg＝kg+1，转至步骤(3-3)，结束条件为寻优达到最大进化代数，或评价值小于给定精度。本发明与现有技术相比，其显著优点在于：(1)采用模糊控制动态调整参数，使其具有更好的控制效果，克服了传统pid算法存在的超调量过大，稳态时间过长等问题；(2)本方法采用粒子群算法来优化比例因子与量化因子；(3)本方法采用了smith算法来克服时滞环节带来的不稳定。附图说明图1为本发明的温度控制系统示意图。图2为本发明的温度控制系统原理图。图3为本发明的smith算法模型原理图。图4为本发明的simulink模型原理图。图5是粒子群算法所得出的比例因子以及量化因子最优值图。图6是普通pid的控制结果图。图7是fuzzy-smith控制结果图。图8为本发明模糊控制过程中kp变化过程图。图9为本发明模糊控制过程中ki变化过程图。图10为本发明模糊控制过程中kd变化过程图。图11为本发明在150s时对系统施加值为3的阶跃冲击后系统响应曲线。具体实施方式下面结合附图及具体实施例对本发明作进一步详细说明。结合图1～4，一种基于3d打印喷头的粒子群模糊smith温度控制方法，包括以下步骤：步骤1，采用atmega2560-16aupwm+gp8101产生可变直流电压，根据系统辨识结果设计模糊pid控制模型；步骤2，建立smith算法模型，得出系统由延时所差生的误差；步骤3，建立粒子群算法程序，得出比例因子和量化因子最优值；步骤4，将上述步骤中所设计的模糊pid算法、smith算法、粒子群算法结合起来，建立整体控制模型。步骤1设计模糊pid控制模型，具体如下：使用atmega2560-16au模拟口产生周期可变的pwm波，将其接入gp8101芯片，产生可变直流电压，将此电压接入加热棒中，使用不同的直流电压进行系统辨识；通过实验，发现本发明所考虑的温度控制系统可以近似为一阶惯性延时系统，其传递函数可大致表现为：s-复频率设计模糊pid控制模型还需要确定输入输出模糊论域、比例因子、模糊子集和隶属度函数、模糊规则、去模糊方法以及量化因子。输入输出模糊论域：在本发明所述的模糊控制模型中，以误差(e)、误差变化率(ec)为输入，以δkp、δki、δkd为输出，误差及误差变化率的模糊论域范围为[-3,3]，δkp、δki、δkd模糊论域的范围也为[-3,3]。比例因子：由于输入模糊论域一般为确定不变的，但实际输入量(误差以及误差变化率)的范围一般是变动的且与模糊论域不一致，所以需要确定一个因子将实际输入转换到模糊论域中，此值先设为未知。模糊子集和隶属度函数：模糊控制的特点在于其能充分地利用人工经验对控制对象进行控制，模糊子集就充分的体现了这一特质，在本发明所述的模糊控制模型中，将模糊论域划分为七个模糊子集，对每一个模糊子集的范围以及隶属度函数详解如下：误差(e)：模糊论域范围为[-3,3]，划分为七个模糊子集{nb,nm,ns,zo,ps,pm,pb}，各模糊子集对应的隶属度函数及其定义域如下表所示；nbgaussmf[0.4248-3]nmtrimf[-3-1.999-1]nstrimf[-1.999-10]zogaussmf[0.031830]pstrimf[011.999]pmtrimf[11.9993]pbgaussmf[0.42543]误差变化率(ec)：模糊论域范围为[-3,3],划分为七个模糊子集{nb,nm,ns,zo,ps,pm,pb}，其隶属度函数以及定义域如下表所示：δkp：模糊论域范围为[-3,3]，划分为七个模糊子集{nb,nm,ns,zo,ps,pm,pb}，其隶属度函数以及定义域如下表所示：nbgaussmf[0.4248-3]nmtrimf[-3-1.999-1]nstrimf[-1.999-10]zotrimf[-101]pstrimf[012]pmtrimf[123]pbgaussmf[0.42543]δki：模糊论域范围为[-3,3]，划分为七个模糊子集{nb,nm,ns,zo,ps,pm,pb}，其隶属度函数以及定义域如下表所示：nbgaussmf[0.4248-3]nmtrimf[-32-1]nstrimf[-2-10]zotrimf[-101]pstrimf[012]pmtrimf[123]pbgaussmf[0.42543]δkd：模糊论域范围为[-3,3],划分为七个模糊子集{nb,nm,ns,zo,ps,pm,pb}，其隶属度函数以及定义域如下表所示：模糊规则的形式为：ifxisaandyisb,thenzisc,其中x,y为输入量，z为输出量，a,b为输入模糊量，c为输出模糊量，此规则由实验确定。去模糊方法：为了获得准确的控制量，就要求去模糊方法能够很好的表达输出隶属度函数的计算结果。本发明采用面积重心法，面积重心法是取隶属度函数曲线与横坐标围成面积的重心，作为模糊推理的最终输出值，公式如下：μ(v)-隶属度函数v-变量值量化因子：由于输入模糊论域一般为确定不变的，但实际输输出量(δkp、δki、δkd)需要与实际控制系统相适应，所以需要确定一个因子将输出模糊量转换成精确量，此值先设为未知。如图3所示，步骤2所述建立smith算法模型，得出系统由延时所差生的误差，步骤如下：带有纯延迟环节的控制系统，由于特征方程中仍会含有延时函数，使得系统稳定性降低，如果延时时间过长，将会使得系统不稳定，此时我们将系统延时所产生的误差算入到总误差内，便可使得系统稳定性大幅度提升，具体方法是，将期望值与实际输出值之差作为误差一，将延时所产生的误差记为误差二，将误差一与误差二之差记为总误差，以此就建立出了smith算法模型。如图5所示，步骤3所述建立粒子群算法程序，得出比例因子和量化因子最优值，过程如下：(3.1)初始化：设定参数的运动范围，设定学习因子c1、c2,最大进化代数g，kg表示当前的进化代数。在一个5维参数的搜索解空间中，粒子组成的种群规模大小为size，每个粒子代表解空间的一个候选解，其中第i(1≤i≤size)个粒子在整个解空间的位置表示为xi，速度表示为vi。第i个粒子从初始到当前迭代次数搜索产生的最优解为个体极值fgbest,整个种群目前的最优解为fzbest。随机产生初始种群的位置矩阵和速度矩阵。(3.2)适应度评价：将各个粒子初始位置作为个体极值，采用适应度函数：f(x)＝∫(t*|e(t)|)dtt-时间e(t)-误差计算群体中各个粒子的初始适应值f(xi)，并求出种群最优位置。(3.3)更新粒子的速度和位置，产生新种群，并对粒子的速度和位置进行越界检查。为避免算法陷入局部最优，加入一个局部自适应变异算子进行调整。更新公式如下：其中，kg＝1,2,……,g,i＝1,2,……,size,r1和r2为0到1的随机数，c1为局部学习因子，c2为全局学习因子。(3.4)比较粒子的当前适应值f(xi)和自身历史最优值fgbesti。如果f(xi)优于fgbesti，则置fgbesti为当前f(xi)，并更新粒子位置。(3.5)比较粒子的当前适应值f(xi)和种群最优值fzbest。如果f(xi)优于fzbest，则置fzbest为当前f(xi)，并更新种群全局最优值。(3.6)检查结束条件，若满足，则结束寻优；否则kg＝kg+1,转至(3)。结束条件为寻优达到最大进化代数，或评价值小于给定精度。步骤4所述将上述步骤中所设计的模糊pid算法、smith算法、粒子群算法结合起来，建立整体控制模型，过程如下：在模糊pid模型中将比例因子以及量化因子设为es、ecs和ps、is、ds，在粒子群程序.m中将输出量也设为es、ecs和ps、is、ds，这样，粒子群算法的输出就成为了模糊pid的输入，同时将模糊pid模型中适应度函数中所需要的量引出作为粒子群算法的输入，这样模糊pid就与粒子群算法结合了起来，最后将smith算法得到的误差引入到总误差中，通过上述步骤整体控制模型建立完毕。图6为kp为、ki为、kd为的传统pid的调节效果，可看出此控制方案超调量较大(约为4)，且稳态时间较长(约为300s)；图7为基于粒子群的fuzzy-simth-pid控制方法，从图6与图7的对比中可知基于粒子群的fuzzy-simth-pid控制方法无超调、稳态时间短，具有远优于传统pid的控制性能。图8反映了kp在fuzzy控制过程中随时间的变化；图9反映了ki在fuzzy控制过程中随时间的变化；图10反映了kd在fuzzy控制过程中随时间的变化；为检测此控制方案的抗干扰能力，在150s时对系统施加一个值为3的阶跃冲击，从图11可看出系统抗干扰能力强，很快就能回到稳态。当前第1页12