一种基于故障敏感慢特征的多块故障监测方法与流程

本发明涉及的工业生产过程故障监测和诊断
技术领域：
，尤其涉及一种基于故障敏感慢特征的多块故障监测方法。
背景技术：
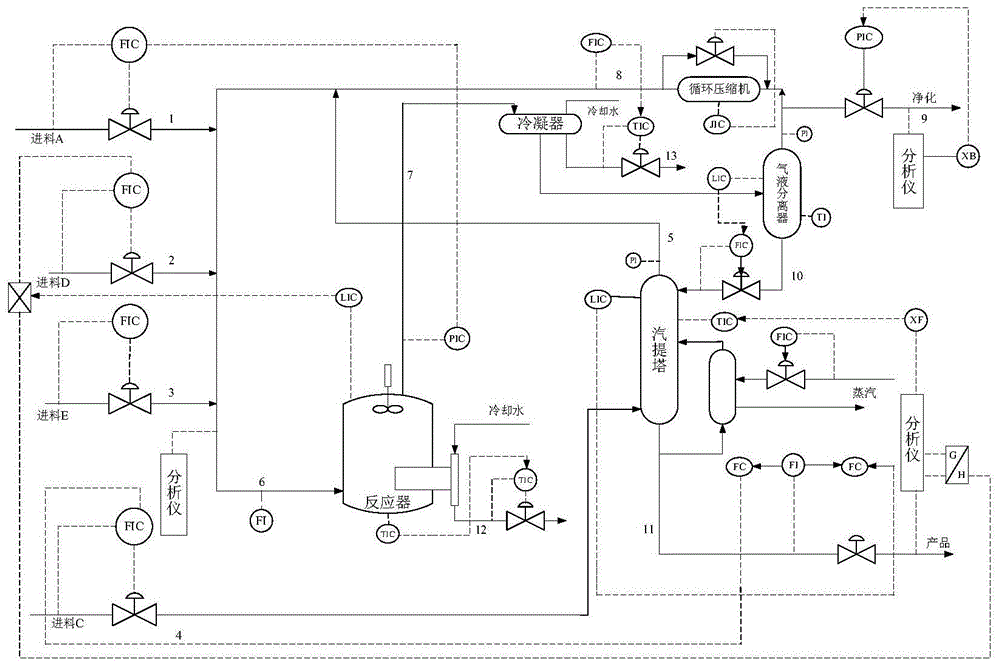
：现代工业生产过程对产品质量和安全性的要求日益提高，若复杂工业过程发生故障，则会造成巨大的损失，因此对过程进行有效的监控至关重要。随着传感和检测技术飞速发展，工业生产的信息化程度不断提高，产生了大量的生产过程数据，因而多元统计过程监控(mspm)方法得到了广泛应用。其中主元分析法(pca)、偏最小二乘(pls)和独立元分析(ica)等是比较经典的多元统计监控方法；然而这些方法都无法有效解决动态和大规模问题。传统的mspm方法是静态过程监视方法，认为样本彼此独立，换言之，当前时刻的样本与过去时刻的样本无关。但是，由于工业过程非常复杂并且具有未知的动态特性，因此静态监视方法将忽略重要的过程动态信息，从而导致监视性能不佳。以大规模和多个操作单元为特征的现代生产过程越来越多，而当这样的生产过程发生故障时，可能只有部分变量受到影响，这时若只建立全局模型，那么局部信息可能会被淹没，因此，多块或分布式过程监控成为一种有效的解决方案。技术实现要素：本部分的目的在于概述本发明的实施例的一些方面以及简要介绍一些较佳实施例。在本部分以及本申请的说明书摘要和发明名称中可能会做些简化或省略以避免使本部分、说明书摘要和发明名称的目的模糊，而这种简化或省略不能用于限制本发明的范围。鉴于上述现有故障监测方法不能有效对动态及大规模过程进行监测，提出了本发明。因此，本发明目的是提供一种基于故障敏感慢特征的多块故障监测方法。为解决上述技术问题，本发明提供如下技术方案：一种基于故障敏感慢特征的多块故障监测方法，包括，采集工业生产系统中的数据，并将所得数据划分为训练集和测试集；对训练集进行慢特征分析，计算出慢特征变换矩阵；定义故障敏感程度系数，并由慢特征变换矩阵中的系数得出各慢特征对故障的敏感程度；定义故障敏感程度阈值，对训练集每一维变量进行故障敏感慢特征的选取，并作为训练子块；对每一个训练子块分别计算故障统计量，并采用支持向量数据描述模型计算出超球体半径作为故障控制限；对每一个测试样本分别计算出故障统计量，带入支持向量数据描述模型中计算出距离球心的距离，通过比较与球心距与半径大小判断是否产生故障。作为本发明所述基于故障敏感慢特征的多块故障监测方法的一种优选方案，其中：采集工业生产系统中数据，并将数据划分为训练集和测试集的步骤包括：通过传感器采集工业生产系统中的数据；根据不同工况，将数据分为正常数据和故障数据；将正常数据作为训练集，其故障数据作为测试集；分别对训练集和测试集进行标准化处理。作为本发明所述基于故障敏感慢特征的多块故障监测方法的一种优选方案，其中：传感器为温度传感器、压力传感器和流量传感器。作为本发明所述基于故障敏感慢特征的多块故障监测方法的一种优选方案，其中：训练集标准化处理步骤包括：计算训练集x的平均值μ；计算训练集x的标准差δ；标准化后的训练集作为本发明所述基于故障敏感慢特征的多块故障监测方法的一种优选方案，其中：测试集y标准化处理的平均值和标准差采用训练集的平均值和标准差；其中，标准化后的测试集y：作为本发明所述基于故障敏感慢特征的多块故障监测方法的一种优选方案，其中：对训练集进行慢特征分析，计算出慢特征变换矩阵的步骤如下：给定一个m维的时序信号，并按照由慢到快的顺序进行排列；取慢特征的问题转为优化问题；对线性慢特征分析进行变换；采用svd分解对数据作白化处理；将优化问题转化为求解正交矩阵；根据白化矩阵和正交矩阵获取慢特征变换矩阵。作为本发明所述基于故障敏感慢特征的多块故障监测方法的一种优选方案，其中：将故障敏感程度系数定义为：εij＝|wij|其中，εij为第i个慢特征对第j维变量上发生故障的敏感程度系数，wij为慢特征变换矩阵中第i行第j列的元素。作为本发明所述基于故障敏感慢特征的多块故障监测方法的一种优选方案，其中：将故障敏感程度阈值定义为：其中，εjlim为第j个变量维度上选择故障敏感慢特征的阈值，为第j个变量维度上最大的故障敏感系数，μ为一个0～1之间的系数。作为本发明所述基于故障敏感慢特征的多块故障监测方法的一种优选方案，其中：慢特征分析模型中故障统计量计算如下：其中，sk为通过故障敏感程度所选择的慢特征矩阵。作为本发明所述基于故障敏感慢特征的多块故障监测方法的一种优选方案，其中：支持向量数据描述模型下的故障统计量与故障控制限如下：s.t.||φ(yi)-a||2≤r2+ξi其中，r是超球体半径；a是超球体球心；惩罚系数c权衡超球体的体积和训练样本的错误率；ξi是松弛变量。其中，上式的优化问题可转化为求解其对偶问题的优化问题：其中，k为核函数；αi为拉格朗日乘子；xi和xj为第i个和第j个训练样本，支持向量为满足0＜αi＜c的样本；其中，通过解决此优化问题，可得超球体半径：其中，测试样本与超球体球心的距离为：本发明的有益效果：本发明通过对统计量计算公式的分析，定义故障敏感程度系数，对慢特征进行重新排序，选择变量方向上对故障最敏感的慢特征，并对每一维变量进行敏感慢特征的选择并进行并行监测，能够有效实现多个维度动态及大规模过程上有效的监测。附图说明为了更清楚地说明本发明实施例的技术方案，下面将对实施例描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动性的前提下，还可以根据这些附图获得其它的附图。其中：图1为本发明基于故障敏感慢特征的多块故障监测方法的te过程的工艺流程图。图2为本发明基于故障敏感慢特征的多块故障监测方法的建模流程图。图3为本发明基于故障敏感慢特征的多块故障监测方法的传统方法pca对te过程故障16的监测结果图。图4为本发明基于故障敏感慢特征的多块故障监测方法对te过程故障16的监测结果图。图5为本发明基于故障敏感慢特征的多块故障监测方法的基于传统慢特征排序下各慢特征的统计量贡献百分比。图6为本发明基于故障敏感慢特征的多块故障监测方法的基于故障敏感程度重新排序后各慢特征的统计量贡献百分比。具体实施方式为使本发明的上述目的、特征和优点能够更加明显易懂，下面结合说明书附图对本发明的具体实施方式做详细的说明。在下面的描述中阐述了很多具体细节以便于充分理解本发明，但是本发明还可以采用其他不同于在此描述的其它方式来实施，本领域技术人员可以在不违背本发明内涵的情况下做类似推广，因此本发明不受下面公开的具体实施例的限制。其次，此处所称的“一个实施例”或“实施例”是指可包含于本发明至少一个实现方式中的特定特征、结构或特性。在本说明书中不同地方出现的“在一个实施例中”并非均指同一个实施例，也不是单独的或选择性的与其他实施例互相排斥的实施例。再其次，本发明结合示意图进行详细描述，在详述本发明实施例时，为便于说明，表示器件结构的剖面图会不依一般比例作局部放大，而且所述示意图只是示例，其在此不应限制本发明保护的范围。此外，在实际制作中应包含长度、宽度及深度的三维空间尺寸。实施例1参照图1，提供了一种基于故障敏感慢特征的多块故障监测方法的整体结构示意图，如图1，一种基于故障敏感慢特征的多块故障监测方法包括步骤，s1：采集工业生产系统中的数据，并将所得数据划分为训练集和测试集；s2：对训练集进行慢特征分析，计算出慢特征变换矩阵；s3：定义故障敏感程度系数，并由慢特征变换矩阵中的系数得出各慢特征对故障的敏感程度；s4：定义故障敏感程度阈值，对训练集每一维变量进行故障敏感慢特征的选取，并作为训练子块；s5：对每一个训练子块分别计算故障统计量，并采用支持向量数据描述(svdd)模型计算出超球体半径作为故障控制限；s6：对每一个测试样本分别计算出故障统计量，带入支持向量数据描述(svdd)模型中计算出距离球心的距离，通过比较与球心距与半径大小判断是否产生故障。本发明针对动态大规模工业过程，提出故障敏感慢特征的概念，通过对统计量计算公式的分析，定义故障敏感程度系数，对慢特征进行重新排序，选择变量方向上对故障最敏感的慢特征；然后基于多块监测的思想，对每一维变量进行敏感慢特征的选择并进行并行监测，这样无论故障发生在哪个维度上都可以对其进行有效的监测；最终将子块监测结果通过svdd融合为一个直观的监测结果，为动态故障监测提供了一种多块监测方法。具体的，本方法包括，s1：采集工业生产系统中的数据，并将数据划分为训练集和测试集；其中，采集工业生产系统中的数据，并将数据划分为训练集和测试集的步骤包括：s11：通过传感器采集工业生产系统(田纳西-伊斯曼过程，高炉炼铁生产设备)中数据；需说明的是，传感器为温度传感器、压力传感器和流量传感器等，工业生产系统为田纳西-伊斯曼过程或高炉炼铁工业生产线涉及到的设备，如反应器、冷凝器、压缩机、分离器和汽提塔等；s12：根据不同工况，将所得数据分为正常数据和故障数据；其中，采集工况包括正常工况和故障工况；s13：将正常数据作为训练集，而故障数据作为测试集；s14：分别对正常数据和故障数据进行标准化处理。需说明的是，训练集标准化处理步骤包括：计算训练集x的平均值μ；计算训练集x的标准差δ；标准化后的训练集需强调的是，测试集y的平均值和标准差采用训练集的平均值和标准差。s2：对训练集进行慢特征分析，计算出慢特征变换矩阵；其中，对训练集进行慢特征分析，计算出慢特征变换矩阵的步骤如下：给定一个m维的时序信号，并按照由慢到快的顺序进行排列；取慢特征的问题转为优化问题；对线性慢特征分析进行变换；采用svd分解对数据作白化处理；将优化问题转化为求解正交矩阵；根据白化矩阵和正交矩阵获取慢特征变换矩阵。具体的，慢特征分析及慢特征变换矩阵的计算如下：给定一个m维的时序信号x(t)＝[x1(t),x2(t),...,xm(t)]，慢特征分析的目的就是找到一个变换函数g(t)＝[g1(t),g2(t),...,gm(t)]以保证提取的目标特征s(t)＝g[x(t)]＝[s1(t),s2(t),...,sm(t)]按照由慢到快的顺序进行排列。提取慢特征的问题可以转为以下优化问题：<si>t＝0(零均值约束)(单位方差约束)<si,sj>t＝0,i≠j(不相关约束)其中si为第i个慢特征；δs为慢特征的一阶差分；<·>为序列的期望。线性慢特征分析可变换成如下形式：s(t)＝wx(t)其中，w为变换矩阵。为了计算出w，首先采用svd分解，对数据作白化处理以满足上述约束。r＝<x(t)x(t)t>t为x(t)的协方差矩阵，对其进行svd分解：r＝uλut其中，u为特征向量矩阵，λ为包含特征值的对角阵，白化矩阵为q＝λ-1/2ut。数据(即训练集)进行白化后可写为：z＝λ-1/2utx＝qx其中，“z”表示对原始数据进行白化处理后的数据；因此，慢特征可由下式得到：s＝wx＝wq-1z＝pz其中，“p”是由训练集提取的慢特征，其p＝wq-1。因为，<z>t＝0，满足第一个约束。约束二和三等效于以下等式：<sst>＝p<zzt>tpt＝ppt＝i因此，上述优化问题可进一步转化为求解正交矩阵p，使得最小。通过对<(δz)(δz)t>进行svd(表示奇异值分解)分解，可得：<(δz)(δz)t>t＝ptωp其中，△z表示z的差分；然后，可由一下等式得到慢特征变换矩阵w：w＝pq＝pλ-1/2uts3：定义故障敏感程度系数，并由慢特征变换矩阵中的系数得出各慢特征对故障的敏感程度；其中，故障敏感程度系数定义如下：εij＝|wij|其中εij为第i个慢特征对第j维变量上发生故障的敏感程度系数，wij为慢特征变换矩阵中第i行第j列的元素。s4：定义故障敏感程度阈值，对训练集每一维变量进行故障敏感慢特征的选取，并作为训练子块；其中，故障敏感程度阈值定义如下：其中为εjlim第j个变量维度上选择故障敏感慢特征的阈值，为第j个变量维度上最大的故障敏感系数，μ为一个0～1之间的系数。s5：对每一个训练子块分别计算故障统计量，并采用支持向量数据描述(svdd)模型计算出超球体半径作为故障控制限；其中：慢特征分析模型中故障统计量计算如下：其中，sk为通过故障敏感程度所选择的慢特征矩阵支持向量数据描述(svdd)模型下的故障统计量与故障控制限如下：s.t.||φ(yi)-a||2≤r2+ξi其中，r是超球体半径；a是超球体球心；惩罚系数c权衡超球体的体积和训练样本的错误率；ξi是松弛变量。上式的优化问题可转化为求解其对偶问题的优化问题：其中，k为核函数；αi为拉格朗日乘子；xi和xj为第i个和第j个训练样本；支持向量为满足0＜αi＜c的样本。通过解决此优化问题，可得超球体半径：作为新的故障控制限。s6：对每一个测试样本分别计算出故障统计量，带入支持向量数据描述(svdd)模型中计算出距离球心的距离，通过比较与球心距与半径大小判断是否产生故障。测试样本与超球体球心的距离为：作为新的故障统计量。若测试样本与超球体球心的距离大于超球体半径，即为超限，超限表示发生故障，将对其进行故障隔离并发送警报提醒；未超限，表示正常。实施例2为了验证所提方法的有效性和可行性，在田纳西-伊斯曼(tennesseeeastman，简称te)软件平台上搭建了五个主要单元：反应器、冷凝器、压缩机、分离器和汽提塔，如图1所示，包含22个过程测量变量、19个成分测量变量以及12个操作变量仿真模型，需说明，te过程模型由伊斯曼化学公司创建并用于评价过程控制和监控方法的一个现实的工业过程；在te过程共预设了21种不同类型的故障，故障类型有阶跃变化、随机变化、缓慢漂移、阀门黏滞，其中16个为已知故障，5个为未知故障；实验中采用正常工况下的960个样本作为训练数据集，故障工况下的960个样本作故障测试集，故障均从第161个样本点引入，表1所示为te过程21种故障描述。表1te过程故障描述采用本发明提出的基于故障敏感慢特征的多块故障监测方法，选取te过程中22个过程测量变量以及除搅拌速度外的11个操作变量共33个变量用于建模与监测，如表2所示。对训练数据集进行慢特征分析，得到慢特征变换矩阵w；通过定义的故障敏感系数εij和阈值εjlim(本方法中μ的值选择为0.6)对33维变量分别进行故障敏感慢特征的选择，因此可得33个子块，具体的分块结果如表3所示。表2te过程监测变量表3子块划分结果子块序号慢特征序号子块序号慢特征序号116,25,27185216,21,321913,3036,7,8,9,20,28204,16,234112132514,15,19,30225,31618237,9,12,14,26,32712,21,26,27247,8,9,20,28814,17,23,25,312516,25,27911,15,21,26,332612,17,271018,21,28,29,302717,21,22,29,31114,8,10,11,22,23,31,322818,21,27,28,29,301222,28,302922,28,301312,14,23,26,2730241416,19,23,25,30,31315,1315243211,15,331614,21,22,23333,4,5173,4,5表4给出了传统pca故障监测方法与本发明方法对te过程18种故障的监测结果，故障3、9、15在诸多方法均难以被监测到，所以在此不做比较。可以看出本发明方法在所有故障情况下的监测结果均优于传统pca故障监测方法(表中数字含义为故障检测率，数值越大说明监测效果越好)。为进一步说明本发明方法的性能，选取故障16做详细分析。图5和图6为pca方法和本发明方法下的监测结果。由图可以看出本发明方法下的故障监测效果明显优于pca方法下的故障监测效果，故障检测率达到0.95。图5为按照传统慢特征排序时各慢特征对应的统计量的贡献百分比，表明对该故障的敏感程度。由图可知，当选择最慢的慢特征对故障进行监测时，可能无法获得最大的统计量贡献值，这是因为最慢的特征不一定对故障最敏感。图6为经过故障敏感程度重新排序后子块31中各慢特征对应的统计量的贡献百分比。由于变量31是故障16发生的主要原因，因此子块31中以敏感系数ε排序的慢特征对故障的敏感程度是依次减少的，由此保证根据阈值选择后的慢特征总是对故障最敏感，进而提升了模型的监测性能。重要的是，应注意，在多个不同示例性实施方案中示出的本申请的构造和布置仅是例示性的。尽管在此公开内容中仅详细描述了几个实施方案，但参阅此公开内容的人员应容易理解，在实质上不偏离该申请中所描述的主题的新颖教导和优点的前提下，许多改型是可能的(例如，各种元件的尺寸、尺度、结构、形状和比例、以及参数值(例如，温度、压力等)、安装布置、材料的使用、颜色、定向的变化等)。例如，示出为整体成形的元件可以由多个部分或元件构成，元件的位置可被倒置或以其它方式改变，并且分立元件的性质或数目或位置可被更改或改变。因此，所有这样的改型旨在被包含在本发明的范围内。可以根据替代的实施方案改变或重新排序任何过程或方法步骤的次序或顺序。在权利要求中，任何“装置加功能”的条款都旨在覆盖在本文中所描述的执行所述功能的结构，且不仅是结构等同而且还是等同结构。在不背离本发明的范围的前提下，可以在示例性实施方案的设计、运行状况和布置中做出其他替换、改型、改变和省略。因此，本发明不限制于特定的实施方案，而是扩展至仍落在所附的权利要求书的范围内的多种改型。此外，为了提供示例性实施方案的简练描述，可以不描述实际实施方案的所有特征(即，与当前考虑的执行本发明的最佳模式不相关的那些特征，或于实现本发明不相关的那些特征)。应理解的是，在任何实际实施方式的开发过程中，如在任何工程或设计项目中，可做出大量的具体实施方式决定。这样的开发努力可能是复杂的且耗时的，但对于那些得益于此公开内容的普通技术人员来说，不需要过多实验，所述开发努力将是一个设计、制造和生产的常规工作。应说明的是，以上实施例仅用以说明本发明的技术方案而非限制，尽管参照较佳实施例对本发明进行了详细说明，本领域的普通技术人员应当理解，可以对本发明的技术方案进行修改或者等同替换，而不脱离本发明技术方案的精神和范围，其均应涵盖在本发明的权利要求范围当中。当前第1页12