一种飞行器编队控制方法与流程

本发明属于飞行器飞行策略技术领域，尤其涉及一种飞行器编队控制方法。

背景技术：

目前对于无人飞行器的编队控制问题，主要有基于领-从模式的编队方法和基于分布式通讯模式的编队方法。例如，基于蚁群算法为飞行器规划相对路径再通过设计航迹跟踪控制率进行跟踪，但是此算法将编队形成与重构问题划分为路径规划与航迹跟踪两部分，求解效率较低；或者，对控制作用及时间分别进行参数化与离散化处理，并分别采用改进的遗传算法、鸽群算法进行寻优，但此类方法计算量较大，且仅适用于二维平面，在三维平面未进行有效验证；最后，还可以采用微粒群算法解算pi控制器参数，虽然实现了有效的编队控制，但此方法未考虑编队重构过程中的耗能问题。此外，与多目标优化算法相比，单目标优化算法的求解结果受代价函数权重的影响较大，当编队形成时间或耗能指标发生变化时，需要重新计算最优解，效率较低。

技术实现要素：

为解决上述问题，本发明提供一种飞行器编队控制方法，能够有效实现飞行器的编队飞行，能满足飞行器间距离约束的效果。

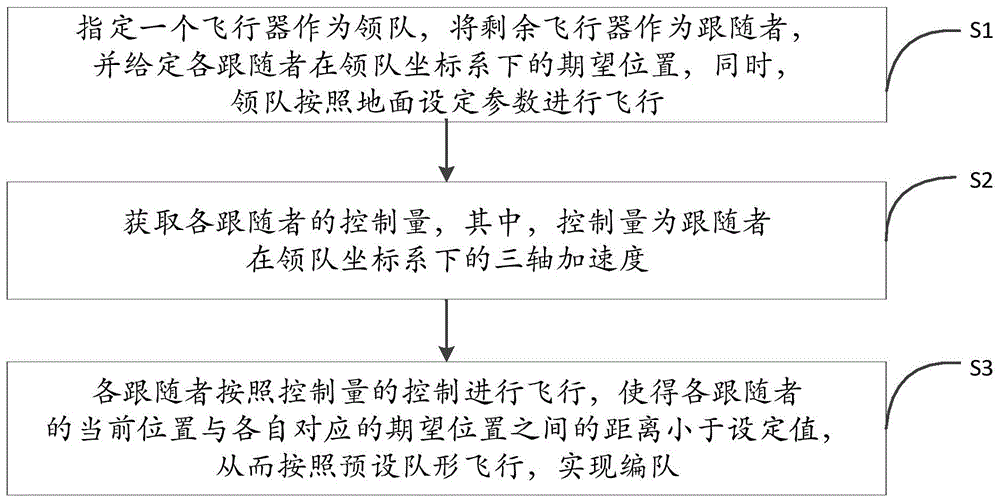
一种飞行器编队控制方法，包括以下步骤：

s1：指定一个飞行器作为领队，将剩余飞行器作为跟随者，并给定各跟随者在领队坐标系下的期望位置，同时，领队按照地面设定参数进行飞行；

s2：获取各跟随者的控制量u，其中，控制量u为跟随者在领队坐标系下的三轴加速度；

s3：各跟随者按照控制量u的控制进行飞行，使得各跟随者的当前位置与各自对应的期望位置之间的距离小于设定值，从而按照预设队形飞行，实现编队。

进一步地，将各跟随者分别作为当前飞行器执行以下步骤，得到各自对应的控制量u：

s21：构建当前飞行器的状态变量x1和期望状态变量如下：

x1＝[xi,yi,zi]^t

其中，xi,yi,zi分别为当前飞行器i在领队坐标系下的坐标，hxi,hyi,hzi分别为当前飞行器i在领队坐标系下的期望位置坐标，且i＝1,2,…,m，m为跟随者的数量，t表示转置；

s22：根据状态变量x1和期望状态变量得到当前飞行器的跟踪误差其中，ex,ey,ez分别为当前飞行器在领队坐标系下三个方向上的跟踪误差；

s23：采用设定边界函数对跟踪误差e1(t)进行如下边界约束，使得跟踪误差e1(t)在设定时间tk内收敛；

s24：采用设定误差变换函数将上述边界约束转换为等式边界约束后，求解所述等式边界约束，得到转换误差ε1(t)的解，同时，构建虚拟控制量x2c，其中，虚拟控制量x2c为转换误差ε1(t)的解的其中一个参数，且虚拟控制量x2c使得跟踪误差e1(t)满足所述边界约束；

s25：构建状态变量x2如下：

x2＝[w1i,w2i,w3i]^t

其中，w1i,w2i,w3i均为中间变量，vfi为当前飞行器i的速度，θfi为当前飞行器i的速度倾角，ψfi为当前飞行器i的速度偏角；

s26：将虚拟控制量x2c进行滤波，得到状态变量x2d；

s27：将状态变量x2d作为状态变量x2待跟踪的变量，并获取两者的跟踪误差e2(t)＝x2-x2d；

s28：将跟踪误差e2(t)＝x2-x2d对时间进行求导，得到

其中，为跟踪误差e2(t)对时间的导数，为状态变量x2对时间的导数，为状态变量x2d对时间的导数；

s29：已知将其代入得到当前飞行器的控制量u为：

其中，k3为大于0的设定常数。

进一步地，所述转换误差ε1(t)的解的计算方法为：

s24a：引入设定误差变换函数ftran(ε1)将不等式边界约束转换为如下等式边界约束：

其中，ε1为转换误差ε1(t)的简写；

s24b：根据所述等式边界约束得到当前飞行器在三轴方向上的跟踪转换误差：

其中，εx,εy,εz分别为当前飞行器在三轴方向上的跟踪转换误差，分别为边界函数在三轴方向上的分量，表示求逆；

s24c：将当前飞行器在三轴方向上的跟踪转换误差作为转换误差ε1＝[εxεyεz]^t，对ε1进行求导可得

其中，为转换误差ε1对时间的导数，为边界函数对时间的导数，为跟踪误差e1(t)对时间的导数；

s24d：已知其中，为的简写，为状态变量x1对时间的导数，为期望状态变量对时间的导数，则有：

其中，θl为领队的弹道倾角，为领队的弹道倾角对时间的导数，ψl为领队的弹道偏角，为领队的弹道偏角对时间的导数，vl为领队的速度。

进一步地，所述边界函数的设定方法为：

s23a：构建边界函数模型如下：

其中，以及分别为边界函数在x、y、z三个方向上的分量，以及为时间t＝0时边界函数在x、y、z三个方向上的初始值，以及为时间趋于无穷时边界函数在x、y、z三个方向上的收敛值，且以及均为大于0的设定常数，pxi、pyi以及pzi分别为x、y、z三个方向上的待定参数；

s23b：在设定时间tk时，当前飞行器在领队坐标系下x、y、z三个方向上的边界值以及需满足如下限定条件：

其中，ex(0)、ey(0)以及ez(0)分别为时间t＝0时，当前飞行器在领队坐标系下三个方向上的跟踪误差，ξ为设定的稳态误差允许范围系数；

s23c：将步骤s23a中的边界函数模型代入步骤s23b中的限定条件，得到待定参数pxi、pyi以及pzi的取值范围：

s23d：构建多目标优化模型：

mintm＝maxtmi

s.t.|axi|≤axmax

|ayi|≤aymax

|azi|≤azmax

其中，tmi为当前飞行器i与期望位置之间的距离小于设定值时的所需时间，i＝1,2,…,m，m为跟随者的数量，tm为编队形成时间，e为形成编队的所需能量，axi、ayi、azi分别为当前飞行器i在领队坐标系下x、y、z三个方向上的加速度，axmax、aymax、azmax分别为当前飞行器i在领队坐标系下x、y、z三个方向上的加速度可取得的最大值；

s23e：在待定参数pxi、pyi以及pzi的取值范围内给三个待定参数取不同的值，得到不同的边界函数使得当前飞行器i对应的跟踪误差e1(t)受不同的边界函数约束，进而得到不同的tm和e；

s23f：将步骤s23e得到的不同的tm和e代入所述多目标优化模型，然后采用快速非支配排序遗传算法求解所述多目标优化模型，得到待定参数pxi、pyi以及pzi的最优解，从而确定边界函数

进一步地，所述虚拟控制量x2c为：

其中，k1、k2为大于零的设定常数。

进一步地，所述地面设定参数包括领队在地面坐标系下的位置坐标，领队的速度、弹道倾角、弹道偏角以及三轴加速度。

有益效果：

1、本发明提供一种飞行器编队控制方法，建立领队-跟随者相对运动模型，采用跟随者在领队坐标系下的三轴加速度作为控制量控制各跟随者的飞行，使得各跟随者的当前位置与各自对应的期望位置之间的距离小于设定值，从而按照预设队形飞行，实现编队；由此可见，本发明能够有效实现飞行器的编队飞行，能满足飞行器间距离约束的效果。

2、本发明提供一种飞行器编队控制方法，将跟随者当前位置与期望位置之间的差值作为跟踪误差，并采用设定边界函数对跟踪误差进行边界约束，使得跟随者的当前位置在给定时间tk内与期望位置之间的距离小于设定值；此外，以编队形成时间、能量消耗为目标函数构建多目标优化模型，然后通过多目标优化模型对边界函数的待定参数进行优化，给出所需能量及形成时间最优的边界函数待定参数取值，也即本发明能够得到最优的边界函数，则在最优边界函数的约束下，编队能满足时间约束和能量约束，进而实现有效的多飞行器的编队飞行。

附图说明

图1为本发明提供的一种飞行器编队控制方法的流程图；

图2为本发明提供的领弹-从弹相对运动关系图；

图3为本发明提供的预设性能反演编队控制器原理框图；

图4为本发明提供的时间限制原理图；

图5为本发明提供的优化结果示意图；

图6为本发明提供的编队的三维轨迹图；

图7为本发明提供的从弹2在x方向上的跟踪误差ex2及边界曲线示意图；

图8为本发明提供的从弹2在y方向上的跟踪误差ey2及边界曲线示意图；

图9为本发明提供的从弹2在z方向上的跟踪误差ez2及边界曲线示意图；

图10为本发明提供的从弹3在x方向上的跟踪误差ex2及边界曲线示意图；

图11为本发明提供的从弹3在y方向上的跟踪误差ey2及边界曲线示意图；

图12为本发明提供的从弹3在z方向上的跟踪误差ez2及边界曲线示意图；

图13为本发明提供的情况1下从弹2的控制量变化曲线示意图；

图14为本发明提供的情况1下从弹3的控制量变化曲线示意图；

图15为本发明提供的情况2下从弹2的控制量变化曲线示意图；

图16为本发明提供的情况2下从弹3的控制量变化曲线示意图。

具体实施方式

为了使本技术领域的人员更好地理解本申请方案，下面将结合本申请实施例中的附图，对本申请实施例中的技术方案进行清楚、完整地描述。

如图1所示，一种飞行器编队控制方法，包括以下步骤：

s1：指定一个飞行器作为领队，将剩余飞行器作为跟随者，并给定各跟随者在领队坐标系下的期望位置，同时，领队按照地面设定参数进行飞行；

需要说明的是，所述地面设定参数包括领队在地面坐标系下的位置坐标，领队的速度、弹道倾角、弹道偏角以及三轴加速度。

例如，以一枚领弹和两枚从弹为例，建立领弹-从弹相对运动模型，并通过在领弹坐标系下描述各从弹的相对位置来描述队形的变换，其相对运动关系如图2所示，axyz为地面坐标系，此处可看作惯性坐标系，olxlylzl为领弹弹道坐标系，ofixfiyfizfi(i＝1,2)分别为从弹i的弹道坐标系。

根据地面坐标系与领队坐标系的转换关系，得到领队在地面坐标系的运动模型为：

式中，xl、yl、zl为领弹在地面坐标系的位置坐标，vl为领弹速度，θl、ψl分别为领弹的弹道倾角和弹道偏角，axl、ayl、azl分别为领弹在地面坐标系上的三轴加速度，其中，axl为切向加速度，ayl、azl为法向加速度，上标的实心点表示对时间求导。

基于领弹和从弹的相对运动关系以及根据地面坐标系与领弹、从弹弹道坐标系之间的相互转换关系，得到从弹在领弹坐标系下的运动模型为

其中，xi、yi、zi(i＝1,2)为从弹i在领弹弹道坐标系的坐标，vfi、θfi、ψfi分别为从弹i的速度、速度倾角和速度偏角，axi、ayi、azi分别为从弹i在领弹坐标系下的三轴加速度，其中，axi为切向加速度，ayi、azi为法向加速度。

s2：获取各跟随者的控制量u，其中，控制量u为跟随者在领队坐标系下的三轴加速度；

s3：各跟随者按照控制量u的控制进行飞行，使得各跟随者的当前位置与各自对应的期望位置之间的距离小于设定值，从而按照预设队形飞行，实现编队。

如图3所示，为预设性能反演编队控制器的原理框图；下面基于预设性能反演编队控制器给出各跟随者的控制量u＝[axi,ayi,azi]^t的获取方式。

将各跟随者分别作为当前飞行器执行以下步骤，得到各自对应的控制量u：

s21：构建当前飞行器的状态变量x1和期望状态变量如下：

x1＝[xi,yi,zi]^t

其中，xi,yi,zi分别为当前飞行器i在领队坐标系下的坐标，hxi,hyi,hzi分别为当前飞行器i在领队坐标系下的期望位置坐标，且i＝1,2,…,m，m为跟随者的数量，t表示转置；

s22：根据状态变量x1和期望状态变量得到当前飞行器的跟踪误差其中，ex,ey,ez分别为当前飞行器在领队坐标系下三个方向上的跟踪误差；

s23：采用设定边界函数对跟踪误差e1(t)进行如下边界约束，使得跟踪误差e1(t)在设定时间tk内收敛；

也就是说，通过设计合理的边界函数，对跟踪误差e1(t)的性能进行预设，实现编队同时满足在队形形成过程中的碰撞避免；设在初始位置误差e1(0)已知且较小的前提下，不等式成立时，误差e1(t)将在函数和的夹逼作用下收敛到一个0的小邻域内；也就是说，根据单调递减的性质，当编队形成时间限制为在tk前形成编队时，可通过设置tk时刻的取值来满足时间约束。

进一步地，所述边界函数的设定方法为：

s23a：构建边界函数模型如下：

其中，以及分别为边界函数在x、y、z三个方向上的分量，以及为时间t＝0时边界函数在x、y、z三个方向上的初始值，令其中k>1，为边界误差放大倍数，ex(0)、ey(0)、ez(0)为t＝0时刻x、y、z三个方向的跟踪误差，以及为时间趋于无穷时边界函数在x、y、z三个方向上的收敛值，且以及均为大于0的设定常数，决定误差收敛的精度，pxi、pyi以及pzi分别为x、y、z三个方向上的待定参数；

s23b：在设定时间tk时，当前飞行器在领队坐标系下x、y、z三个方向上的边界值以及需满足如下限定条件：

其中，ex(0)、ey(0)以及ez(0)分别为时间t＝0时，当前飞行器在领队坐标系下三个方向上的跟踪误差，ξ为设定的稳态误差允许范围系数，通常取±0.02或±0.05，令即可使跟踪误差e(t)在tk前收敛至误差允许范围内，如图4所示；

s23c：将步骤s23a中的边界函数模型代入步骤s23b中的限定条件，得到待定参数pxi、pyi以及pzi的取值范围：

需要说明的是，由于各飞行器平台所能携带的燃料是有限的，因此可以将编队重构问题描述为尽量满足燃料消耗少、调整时间短的优化问题，基于nsga-ii算法以编队形成时间及所需能量作为目标函数进行优化，具体如步骤s23d所示。

s23d：构建多目标优化模型，将编队形成问题看作是关于编队形成所需时间、能量的优化问题：

mintm＝maxtmi

s.t.|axi|≤axmax

|ayi|≤aymax

|azi|≤azmax

其中，tmi为当前飞行器i与期望位置之间的距离小于设定值时的所需时间，也即当前飞行器i到期望位置的距离满足稳态误差允许范围时的所需时间，i＝1,2,…,m，m为跟随者的数量，tm为编队形成时间(各飞行器均到达稳态误差允许范围内)，e为形成编队的所需能量，axi、ayi、azi分别为当前飞行器i在领队坐标系下x、y、z三个方向上的加速度，axmax、aymax、azmax分别为当前飞行器i在领队坐标系下x、y、z三个方向上的加速度可取得的最大值；

s23e：在待定参数pxi、pyi以及pzi的取值范围内给三个待定参数取不同的值，得到不同的边界函数使得当前飞行器i对应的跟踪误差e1(t)受不同的边界函数约束，进而得到不同的tm和e；

s23f：将步骤s23e得到的不同的tm和e代入所述多目标优化模型，然后采用快速非支配排序遗传nsga-ii算法求解所述多目标优化模型，得到待定参数pxi、pyi以及pzi的最优解，从而确定边界函数

s24：采用设定误差变换函数将上述边界约束转换为等式边界约束后，求解所述等式边界约束，得到转换误差ε1(t)的解，同时，构建虚拟控制量x2c，其中，虚拟控制量x2c为转换误差ε1(t)的解的其中一个参数，且虚拟控制量x2c使得跟踪误差e1(t)满足所述边界约束；

需要说明的是，为了降低处理不等式的难度，在系统设计中，通过引入误差变换函数ftran(·)将不等式约束转为等式约束再进行处理；进一步地，所述转换误差ε1(t)的解的计算方法为：

s24a：引入设定误差变换函数ftran(ε1)将不等式边界约束转换为如下等式边界约束：

其中，ε1为转换误差ε1(t)的简写；ftran(ε1)可逆，且满足性质：①光滑且单调递增；②-1<ftran(ε1)<1；③

s24b：根据所述等式边界约束得到当前飞行器在三轴方向上的跟踪转换误差：

其中，εx,εy,εz分别为当前飞行器在三轴方向上的跟踪转换误差，分别为边界函数在三轴方向上的分量，表示求逆；

s24c：将当前飞行器在三轴方向上的跟踪转换误差作为转换误差ε1＝[εxεyεz]^t，对ε1进行求导可得

其中，为转换误差ε1对时间的导数，为边界函数对时间的导数，为跟踪误差e1(t)对时间的导数；

s24d：已知其中，为的简写，为状态变量x1对时间的导数，为期望状态变量对时间的导数，则有

其中，θl为领队的弹道倾角，为领队的弹道倾角对时间的导数，ψl为领队的弹道偏角，为领队的弹道偏角对时间的导数，vl为领队的速度。

所述虚拟控制量x2c为：

其中，k1、k2为大于零的设定常数。将x2c带入的表达式可知ε1满足闭环动力学方程因此ε1有界，不等式约束成立，进而跟踪信号满足预设性能要求。

s25：构建状态变量x2如下：

x2＝[w1i,w2i,w3i]^t

其中，w1i,w2i,w3i均为中间变量，vfi为当前飞行器i的速度，θfi为当前飞行器i的速度倾角，ψfi为当前飞行器i的速度偏角；

s26：将虚拟控制量x2c进行滤波，得到状态变量x2d；

具体的，考虑到微分膨胀问题，采用低通滤波器进行滤波

其中，τ为时间常数；

s27：将状态变量x2d作为状态变量x2待跟踪的变量，并获取两者的跟踪误差e2(t)＝x2-x2d；

s28：将跟踪误差e2(t)＝x2-x2d对时间进行求导，得到

其中，为跟踪误差e2(t)对时间的导数，为状态变量x2对时间的导数，为状态变量x2d对时间的导数；

s29：已知将其代入得到当前飞行器的控制量u为：

其中，k3为大于0的设定常数。

需要说明的是，计算得到的即为当前飞行器的三轴加速度。

由此可见，本发明基于预设性能理论设计控制器，给定编队形成时间约束并初步计算边界函数待定参数的取值范围，以编队形成时间、消耗能量为目标函数，通过nsga-ii算法进行优化，得到边界函数待定参数的帕累托前沿解；对比已有技术，本发明能够有效实现多飞行器的编队飞行，具有能满足预设的编队形成时间约束，并给出所需能量及形成时间最优的边界函数待定参数取值的效果。

下面对于上述基于预设性能控制的编队飞行方法进行仿真验证。

假设领弹弹1和两枚从弹弹2、弹3编队飞行。领弹的相对位置为(0,0,0)m，速度vl＝50m/s，弹道倾角θl0＝0°、弹道偏角ψl0＝0°。两从弹相关参数如下表所示。

表1从弹相关参数

考虑到导弹的过载约束，设三枚导弹的最大切向加速度为axmax＝80m/s²，法向加速度为aymax＝azmax＝100m/s²。预设性能控制器的性能指标函数参数k＝1.2、控制器参数k1＝k2＝10^-4、k3＝10，滤波器时间常数τ＝0.1。令ξ＝0.02、tk＝50s，设计变量取值px2＝py2＝pz2＝a,px3＝py3＝pz3＝b，根据待定参数pxi、pyi以及pzi的取值范围可知，为满足编队形成时间限制，设计变量取值范围为a≥0.1174，b≥0.1233。

通过nsga-ii算法进行优化，为保证种群的多样性，选取交叉概率为0.8，变异概率为0.3，初始种群规模为100，迭代次数为5次，当不满足约束条件时，代价函数取值为10⁷。根据上述参数进行仿真，得到优化结果如图5所示。

从图5中可见，编队形成时间较短时耗费能量较大，形成时间较长时耗费能量较小。当设计变量取值为a＝0.1174、b＝0.1239时，编队形成时间为tm＝41s，所需能量最少为e＝1924；当设计变量取值为a＝0.2018、b＝0.2008时，编队形成时间最短为tm＝25.3，所需能量为e＝4391。分别将以上两组设计变量取值带入性能函数，得到编队的三维轨迹如图6所示。

图7～图9分别为从弹2在x、y、z三个方向上的跟踪误差与边界曲线示意图；图10～图12分别为从弹2在x、y、z三个方向上的跟踪误差与边界曲线示意图；当边界函数的参数取值满足所需能量e最少时，跟踪误差及边界函数如图7～图12中情况1所示，当取值满足编队形成时间tm最短时，跟踪误差及边界函数如图7～图12中情况2所示。与情况1相比，情况2的性能函数收敛速度更快，由于跟踪误差始终位于性能函数范围内，因此情况2的跟踪误差能够更快的收敛到稳态误差允许范围内，即编队形成时间较短。从图7-12中可见，在两组参数下，从弹2、从弹3的跟踪误差均在边界函数上下边界范围内，因此，采用此控制方法能够使编队的瞬态过程与稳态精度满足预设条件。

图13～图14分别为情况1下从弹2、从弹3的控制量变化曲线示意图；图15～图16分别为情况2下从弹2、从弹3的控制量变化曲线示意图；从图13-16中可知，在队形变换过程中，与情况2相比(图15、16)，情况1(图13、14)的控制量绝对值较小，因此，根据多目标优化模型可知情况1形成编队所消耗的能量较小。

由以上结果可知，通过优化分别获得了编队形成时间最短、所需能量最小的边界函数参数pxi、pyi以及pzi，在实际作战中，可充分考虑战场态势及能量、时间约束，得到满足约束的的控制器参数，仿真结果表明采用此控制方法能够在满足编队形成时间约束的前提下形成良好的编队。

当然，本发明还可有其他多种实施例，在不背离本发明精神及其实质的情况下，熟悉本领域的技术人员当然可根据本发明作出各种相应的改变和变形，但这些相应的改变和变形都应属于本发明所附的权利要求的保护范围。