一种欠驱动VTOL飞行器的自耦PD控制理论方法与流程

非最小相位欠驱动非线性系统控制，飞行器控制。

背景技术：

垂直起降(verticaltake-offandlanding,vtol)飞行器因其起飞距离短和垂直起降的性能，因而在军用与民用领域都具有极其重要的作用，已经成为各国争相研究的飞行器对象。由于vtol飞行器存在三个运动自由度却只有两个控制输入，因而是一个典型的欠驱动系统。由于vtol飞行器不仅具有欠驱动特性和非线性耦合特性，而且还是一个非最小相位系统，因而使其控制问题变得更为复杂，引起了控制领域许多国内外学者的广泛关注。迄今为止，有关vtol飞行器的控制方法主要有：状态反馈控制方法、反演(backstepping)控制方法、动态面控制方法、滑模控制方法以及逆最优反馈控制、双闭环pid控制方法、非线性信息融合控制方法等。尽管现有这些控制方法都获得了有效的控制结果，然而状态反馈控制方法存在动态品质与稳态性能欠佳的局限性；backstepping控制方法存在微分爆炸的局限性；动态面控制、滑模控制、逆最优反馈控制以及非线性信息融合控制等控制方法均存在结构复杂、计算量大的局限性；而双闭环pid控制方法则存在增益鲁棒性差与抗扰动鲁棒性差的局限性。

为了有效改善欠驱动vtol飞行器控制系统的动态品质与稳态性能、减小计算量、提高实时性、增强控制系统的鲁棒稳定性和抗扰动鲁棒性，当务之急是发明一种控制器结构简单、参数整定容易、控制系统动态品质与稳态性能良好、抗扰动鲁棒性强的控制理论方法。

技术实现要素：

本发明提供一种欠驱动vtol飞行器的自耦pd(auto-couplingproportional-differrenttial，acpd)控制理论方法，其特征在于，包括如下步骤：

1)根据vtol飞行器质心坐标的期望轨迹x1d、x3d和期望滚转姿态角x5d＝0，可得huygens振动中心坐标的期望轨迹为：

z1d＝x1d-εsinx5d＝x1d，z3d＝x3d+εcosx5d＝x3d+ε

其中，ε0是滚转力矩对横向与纵向运动的耦合作用系数，m和j分别是vtol飞行器的质量和沿纵向轴的转动惯量；

2)根据步骤1)计算横向位置跟踪误差及其误差微分：

e11＝z1d-z1，

其中，z1＝x1-εsinx5，x1和x5分别是vtol飞行器的横向位置与滚转姿态角，

3)根据步骤2)定义横向位置acpdy控制器为：

其中，zcy>0是acpdy控制器的速度因子；

4)根据步骤1)计算纵向位置跟踪误差及其误差微分：

e31＝z3d-z3，

其中，z3＝x3+εcosx5,x3是vtol飞行器的纵向位置，

5)根据步骤4)定义纵向位置acpdz控制器为：

其中，zcz>0是acpdz控制器的速度因子,g是重力加速度；

6)根据步骤3)和5)形成控制力u1和vtol飞行器的底部推力ut：

ut＝mu1

7)根据步骤3)和5)形成vtol飞行器的滚转姿态角虚拟指令：

x5r＝-atan(uy/uz)

8)根据步骤7)计算滚转姿态角跟踪误差及其微分：

e51＝x5r-x5，

9)根据步骤8)定义滚转姿态角的acpd2控制器u2，并形成vtol飞行器的滚转力矩um：

um＝ju2

其中，zc2>0是acpd2控制器的速度因子。

本发明首先通过坐标变换将vtol飞行器的质心映射为huygens振动中心，不仅能实现新系统控制输入解耦，而且也能避免非最小相位vtol飞行器零动态不稳定的问题；然后对huygens振动中心分别设计纵横向位置的acpd控制器，并分别获得vtol飞行器底部推力和滚转姿态角虚拟指令，进而设计滚转姿态角的自耦pd控制器来形成滚转力矩；最后通过复频域分析理论证明闭环控制系统的鲁棒稳定性和抗扰动鲁棒性。理论分析和仿真结果都表明了本发明的有效性，在非最小相位欠驱动vtol控制系统领域具有重要的科学意义和广泛的应用前景。

附图说明

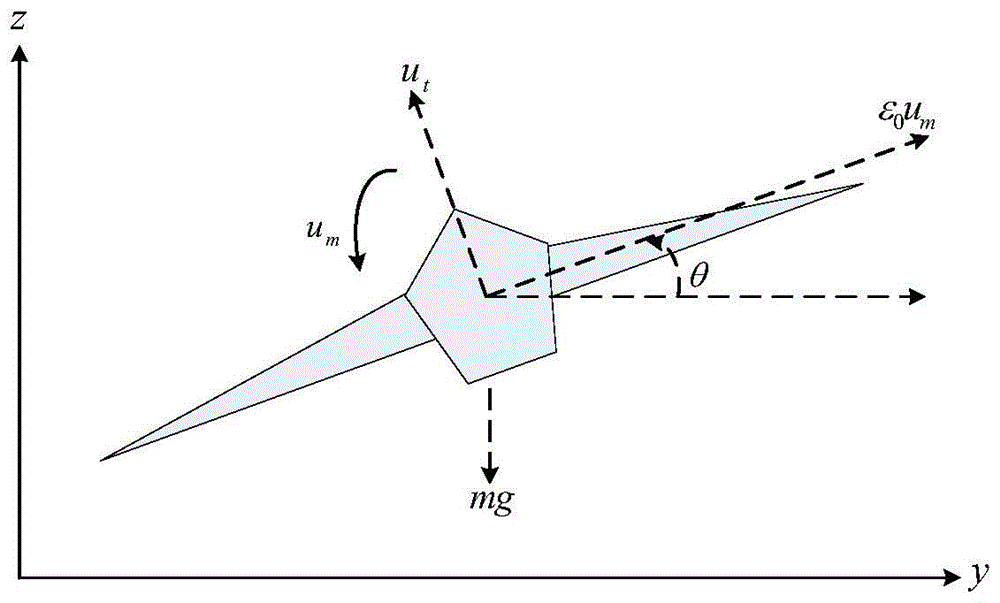
图1欠驱动vtol飞行器模型。

图2vtol飞行器垂直起飞、悬停、着陆等工况过程的控制结果，(a)横向位置跟踪轨迹,(b)纵向位置跟踪轨迹，(c)滚转姿态角跟踪轨迹,(d)底部推力控制输入，(e)滚转力矩控制输入。

具体实施方式

1.欠驱动vtol飞行器模型及其映射

1.1欠驱动vtol飞行器模型

考虑某欠驱动vtol飞行器系统：

其中，状态变量y、z和θ分别是vtol飞行器质心在参考坐标中的横、纵向位置与滚转姿态角；m和j分别是飞行器的质量和沿纵向轴的转动惯量；g为重力加速度；控制输入ut与um分别是底部垂向推力与滚转力矩；ε0是滚转力矩对横向与纵向运动的耦合作用系数。

由于vtol飞行器(1)有三个自由度y、z和θ,却只有两个控制输入ut与um,因而是一类典型的欠驱动非线性耦合系统。

为了便于分析,设状态变量分别为：x1＝y，x3＝z，x5＝θ，则系统(1)可表示为系统(2)的形式；再设则系统(2)可简写为系统(3)的形式。

由系统(3)可知，u2不仅与u1之间存在耦合作用，而且与系统滚转姿态角x5＝θ也存在耦合作用，使得vtol飞行器系统的控制更为复杂。

1.2.欠驱动vtol飞行器模型映射

对系统(3)做如下坐标变换：

z1＝x1-εsinx5，

z3＝x3+εcosx5，

则系统(3)可以表示为式(4)的形式。

显然，上述坐标变换不仅使新的vtol飞行器系统(4)实现了输入解耦的作用，而且使vtol飞行器系统(3)的不稳定质心位置(x1,x3)映射到具有平坦输出的huygens振动中心(z1,z3)。

由于新的vtol飞行器系统(4)的输出是平坦的(z1与z3均不受u2的影响)，因而有效避免了非最小相位vtol飞行器零动态不稳定的问题。由于系统(4)与系统(3)或系统(2)是等价映射，因此由vtol飞行器系统(4)设计的控制器u1和u2可以实现对系统(3)或系统(2)的有效控制。如何对系统(4)施加有效控制，正是本发明的核心技术，即acpd控制技术。

2.vtol飞行器控制系统设计

2.1vtol飞行器的基本控制思想

为了便于分析，设uy与uz分别为：

则vtol飞行器系统(4)可简化为式(7)的形式：

根据式(5)与式(6),可得u1和x5分别如下：

x5＝-atan(uy/uz)(9)

显然，只要设计好横纵向位置的控制器uy与uz，即可获得控制力u1，从而获得vtol飞行器底部垂向推力ut＝mu1；如果设滚转姿态角虚拟指令为：

x5r＝-atan(uy/uz)(10)

则可设计vtol飞行器滚转姿态角控制器u2，进而获得滚转力矩um＝ju2。

2.2.vtol飞行器底部推力控制器设计

设vtol飞行器质心坐标的期望轨迹为x1d与x3d，并设期望滚转姿态角为x5d＝θd＝0，从而可得huygens振动中心坐标的期望轨迹为：

z1d＝x1d-εsinx5d＝x1d(11)

z3d＝x3d+εcosx5d＝x3d+ε(12)

1)横向位置acpdy控制器设计

设横向位置跟踪误差为：

e11＝z1d-z1(13)

其中，z1d＝x1d，z1＝x1-εsinx5。

由式(13)和系统(7)可得横向跟踪误差的微分为：结合系统(7)，可得横向位置受控误差系统为：

在忽略积分环节的情况下，设计横向位置acpdy控制器为：

其中,zcy>0是acpdy控制器的速度因子。

2)纵向位置acpdz控制器设计

设纵向位置跟踪误差为：

e31＝z3d-z3(16)

其中，z3d＝x3d+ε，z3＝x3+εcosx5。

由式(16)和系统(7)可得纵向位置跟踪误差的微分为：结合系统(7)，可得纵向位置受控误差系统为：

在忽略积分环节的情况下，设计纵向位置acpdz控制器为：

其中，zcz>0是acpdz控制器的速度因子，g是重力加速度。

3)vtol飞行器底部推力控制输入

根据式(15)与(18)分别获得横纵向位置控制力uy与uz后，根据式(8)即可获得控制力u1为：

进而可获得欠驱动vtol飞行器底部垂向推力：ut＝mu1。

2.3.vtol飞行器滚转力矩控制器设计

根据式(15)与(18)分别获得横纵向位置控制器uy与uz后，再根据式(10)即可获得滚转姿态角虚拟指令：x5r＝-atan(uy/uz)。设滚转姿态角跟踪误差为：

e51＝x5r-x5(20)

由式(20)和系统(7)可得滚转角跟踪误差的微分为:结合系统(7)，可得姿态角受控误差系统为：

在忽略积分环节的情况下，设计滚转姿态角acpd2控制器为：

其中，zc2>0是acpd2控制器的速度因子。

由式(22)即可获得欠驱动vtol飞行器的滚转力矩为：um＝ju2。

2.4闭环控制系统分析

定理1设则当且仅当zcy>0时，vtol飞行器的横向位置闭环控制系统是有界输入有界输出稳定的。

证明：将式(15)定义的横向位置控制力uy代入受控误差系统(14)，可得横向位置闭环控制系统如下：

考虑到误差初始状态：因此，对系统(23)取单边拉普拉斯变换，并整理得：

其中，系统(24)的第一项是零输入响应：第二项是零状态响应：

定义横向位置闭环系统的传输函数为：

当zcy>0时，由于hy(s)在复频域的左半平面有双重实极点sp＝-zcy<0，因而系统(25)或(24)是有界输入有界输出稳定的，证毕。

定理2设有界：|dy|≤εy<∞，则当且仅当zcy>0时，vtol飞行器的横向位置闭环控制系统具有良好的抗扰动鲁棒性。

证明：根据系统传输函数(25)，闭环系统(24)可简化为：

e11(s)＝e11x(s)+hy(s)dy(s)(26)

其中，

由系统(25)，可得单位冲激响应为：

hy＝texp(-zcyt)(27)

因而闭环系统(26)的时域解可表示为:

e11＝e11x+hy*dy(28)

其中，“*”表示卷积积分运算。

由式(28)可得误差的微分如下：

其中，

当zcy>0时，因此，只要|dy|≤εy<∞，则必有：

以上分析表明：当zcy>0时，只要满足有界条件：|dy|≤εy<∞，横向位置闭环系统(23)则可以从任意不为零的初始误差状态向稳定的平衡点原点(0,0)趋近，理论上可以实现零误差跟踪控制。当zcy>0时，由于e11→0和e12→0只与|dy|≤εy<∞有关，与的具体模型无关，因而acpdy闭环控制系统具有良好的抗扰动鲁棒性，证毕。

为了节省篇幅，欠驱动vtol飞行器的纵向位置闭环控制系统和滚转姿态角闭环控制系统的分析不再赘述，可参照定理1和定理2进行鲁棒稳定性分析。

2.5自适应速度因子

由定理1和定理2可知：当且仅当zcy>0时，欠驱动vtol飞行器的横向位置控制系统是有界输入有界输出稳定的，表明acpdy控制器的速度因子具有很大的整定裕度，因而横向位置控制系统是大范围稳定的。同理，纵向位置控制系统与滚转姿态角控制系统也是大范围稳定的。然而，当acpdy、acpdz和acpd2等三个自耦pd控制器的速度因子zcy、zcz和zc2均较大时，由于比例控制力与微分控制力均较大，尽管可以加快控制系统的响应速度、增强抗扰动能力，然而也很可能会使系统输出存在超调现象，并使控制力出现震荡现象，不利于执行机构；当速度因子均较小时，由于比例控制力与微分控制力均较小，因而不仅会降低控制系统的响应速度，而且也会降低稳态控制精度和抗扰动能力。因此，为了获得控制系统良好的动态品质与稳态性能，应该使用自适应速度因子。

考虑到误差微分的敏感特性，定义acpdy、acpdz和acpd2等三个自耦pd控制器的自适应速度因子模型分别为：

zcy＝zcmyexp(-|e12|)(30)

zcz＝zcmzexp(-|e32|)(31)

zc2＝zcm2exp(-|e52|)(32)

其中，zcmy、zcmz与zcm2分别是横纵向位置与滚转姿态角等三个控制器acpdy、acpdz与acpd2的最大速度因子。

此外，考虑到横纵向位置应该同时到达期望轨迹的坐标点，因而其控制器的最大速度因子应该相同：zcmy＝zcmz；再考虑到滚转姿态角的虚拟指令是由横纵向控制力形成的，即x5r＝-atan(uy/uz)，因而要求滚转姿态角控制器acpd2的最大速度因子zcm2应该满足如下不等式条件：

5zcmy≤zcm2≤10zcmy(33)

3.仿真结果与分析

为了验证本发明的有效性，设欠驱动vtol飞行器的相关参数为：飞行器质量m＝5×10⁴kg，耦合系数ε0＝0.05，转动惯量j＝2×10⁵kg·m²。设采样频率fs＝1000hz，重力加速度g＝9.8m·s^-2；huygens振动中心坐标为：z1＝x1-εsinx5，z3＝x3+εcosx5。

在下列实验中，三个控制器的最大速度因子分别设置为：zcmy＝zcmz＝10，zcm2＝80，因此，欠驱动vtol飞行器控制系统整体组成结构如下：

1)acpdy控制器：

其中，zcy＝10exp(-|e12|)；e11＝z1d-z1，z1＝x1-εsinx5，z1d＝x1d；x1d和x1分别是vtol飞行器质心横向坐标期望值与实际值。

2)acpdz控制器：

其中,zcz＝10exp(-|e32|)，e31＝z3d-z3，z3＝x3+εcosx5,z3d＝x3d+ε；x3d和x3分别是vtol飞行器质心纵向坐标期望值与实际值，

分别获得uy与uz后，可形成控制力u1为：考虑到输入受限情况，要求：6≤u1≤12，进而可获得欠驱动vtol飞行器底部垂向推力为：ut＝mu1。

3)acpd2控制器：

其中,zc2＝80exp(-|e52|)；e51＝x5r-x5，x5r＝-atan(uy/uz)，且|x5r|≤0.3rad。

考虑到输入受限情况，要求：|u2|≤80，进而可获得欠驱动vtol飞行器的滚转力矩：um＝ju2。

为了避免速度测量(无速度传感器)和期望指令的微分运算，三个控制器涉及的误差微分使用差商来近似表示：其中,ts是采样周期；同理，e32≈(e31-e31-1)/ts，e52≈(e51-e51-1)/ts。

设vtol飞行器的横向期望轨迹为x1d＝10米，期望滚转姿态角x5d＝0，纵向期望轨迹为：

设vtol飞行器的初始状态为使用本发明的仿真结果如图2所示。由图2可知，本发明控制方法对欠驱动vtol飞行器垂直起飞、悬停与着陆等全工况过程进行控制，获得了良好的动态品质和稳态性能，表明了本发明控制方法的有效性。

4.结论

针对欠驱动vtol飞行器的控制问题，发明了一种自耦pid控制方法，在复频域分析了闭环控制系统的鲁棒稳定性，仿真结果表明了本发明控制方法的有效性，不仅具有良好的动态品质和稳态性能，而且控制系统结构简单、计算量小、便于实际应用。仿真实验还发现：最大速度在2≤zcmy＝zcmz≤14且5zcmy≤zcm2≤10zcmy的范围内，本发明控制方法都能实现有效控制，因而是一类大范围鲁棒稳定的控制方法。

本发明在欠驱动vtol飞行器控制领域具有重要的科学意义与广泛的应用价值。