一种X对称结构测量无人机姿态角的方法

一种x对称结构测量无人机姿态角的方法
技术领域
1.本发明属无人机领域，具体涉及一种x对称结构测量无人机姿态角的方法。


背景技术：

2.无人机具有体积小、成本低、机动性好、隐身能力强等优点而广泛应用于国防军工、运输、交通、地质、农业等领域。
3.无人机在飞行过程中，获得准确的飞行姿态数据非常重要，这些姿态数据包括翻滚角、俯仰角、巡航角和对应的角速度和加速度等。无人机的控制端利用这些姿态数据可以很好的控制电机运转，保证无人机飞行过程的平稳和飞行方向的正确。
4.现有的无人机姿态数据获取的方法是采用3轴、6轴、9轴传感器进行获取，比较经典的是mpu6050系列产品，为全球首例整合性6轴运动处理组件，而且提供广泛的通用接口如i2c,spi和uart。该模块的姿态获取通常结合卡尔曼滤波算法进行修正，由此获得较好的角度、角速度和加速度数据。
5.但无人机在飞行时处于非常复杂的环境中，不仅飞行旋翼受到电信号本身扰动的影响，而且外部空气漩涡的不同也将导致无人机各个方位的姿态数据非常复杂，因此传统的将6轴传感器放置于中心的方法并不能消除上述影响。将多个传感器置于十字形或者正方形四个角落会在一定程度上取得效果，但一直以来，由于多个传感器的存在会加重cpu演算负担，而且传统的方法也无法解决飞行过程中空间变换的复杂性问题，从而多个传感器的技术无法获得实际应用发展。
6.本技术提供一种新型的x对称结构测量无人机姿态角的方法，该方法将传统技术进行拓展，更重要的是利用了空间群论变换的知识对不同方位获得的数据进行分类演算，提高了演算效率，节约了演算时间，从而解决飞行过程中空间变换的复杂性问题，使得将多个传感器放置于不同对称位置的技术能真正应用于实际中。


技术实现要素：

7.本发明的目的在于提供一种x对称结构测量无人机姿态角的方法，通过三维空间x结构对称放置的6轴传感器，获取无人机各方位姿态数据，而后通过群论算法对无人机各方位姿态数据进行演算，获得无人机飞行过程中的姿态数据，实现无人机飞行控制的准确性。
8.为实现上述目的，本发明的技术方案是：一种x对称结构测量无人机姿态角的方法，通过三维空间x结构对称放置的6轴传感器，获取无人机各方位姿态数据，而后通过群论算法对无人机各方位姿态数据进行演算，获得无人机飞行过程中的姿态数据，实现无人机飞行控制的准确性。
9.在本发明一实施例中，所述传感器至少为4个，并且按照空间x结构进行对称性摆放，以无人机中心为对称心，形成体心对称结构。
10.在本发明一实施例中，所述传感器采用mpu6050系列6轴传感器模块，其基于c、c++进行数据的采集和处理，获得姿态数据。
11.在本发明一实施例中，所述群论算法搭载于stm32f4以上系列或采用windows微小板上，群论算法采用基于stm32的编译软件或采用windows下的python编译。
12.在本发明一实施例中，所述通过群论算法对无人机各方位姿态数据进行演算，获得无人机飞行过程中的姿态数据的具体实现方式如下：
13.传感器以三维空间x结构对称放置，分别测量得到角度、角速度和加速度数据，设传感器获得的角度、角速度和加速度为3*3矩阵：
[0014][0015]
其中，x11-x13分别为三个角度，即：翻滚角、俯仰角和巡航角，x21-x23分别为三个方向的角速度，x31-x33分别为三个加速度值，因此，四个传感器将构成一个6*6阶的矩阵，即：
[0016][0017]
简化为：
[0018][0019]
由于体心对称性，因此对角线的两个传感器x
c1
和x
c3
，x
c2
和x
c4
中的部分矩阵元将成线性相关性，即：
[0020][0021][0022]
x
11-x
41
＝x
12-x
42
＝x
13-x
43
＝λ
ꢀꢀ
(4)
[0023]
同理，其他相关矩阵元也都有类似的关系，将该关系代入矩阵x
t
中，进一步简化矩阵元；
[0024]
通过四个传感器获得的无人机各方位姿态数据需转换后，才可获得无人机机体的角度、角速度和加速度值，无人机机体的最终的矩阵形式为3*3阶矩阵：
[0025][0026]
根据矩阵运算和空间群变换理论，需要引入一个3*6阶的中间矩阵xz才能将四个传感器的6*6阶矩阵变成3*3矩阵，即满足：
[0027]
xz*x
t
*x
zt
＝xfꢀꢀ
(6)
[0028]
其中，x
zt
为xz的转置矩阵，如此即可通过4个x对称的传感器得到无人机各方位姿
态数据，最后通过对称性演算获得无人机机体的最终姿态数据。
[0029]
在本发明一实施例中，所述中间矩阵xz根据x结构通过如下基本矩阵形式进行变换：
[0030][0031]
相较于现有技术，本发明具有以下有益效果：
[0032]
1.由于采用具有空间x对称性结构的传感器放置方式，使得获取无人机在旋翼方向的姿态数据变得更为准确；
[0033]
2.对称性结构降低了传感器使用的成本，避免了大规模使用传感器进行多方位的数据采集；
[0034]
3.空间群变换、群论、坐标变换等融合算法，尤其是群论算法的引入，大幅度降低了无人机在空中飞行时飞行状态的复杂性，通过空间群分类处理，提高了效率并降低了演算时间，使得多传感器配合得以实际应用。
附图说明
[0035]
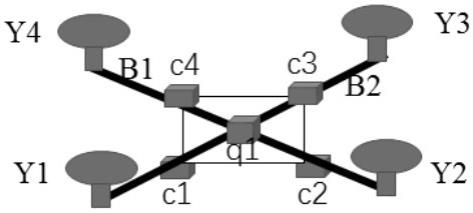
图1为本发明一实例的四旋翼无人机x对称结构测量姿态角示意图。
[0036]
图2为本发明一实例的x对称结构测量无人机姿态角的方法(空间群图)。
具体实施方式
[0037]
下面结合附图，对本发明的技术方案进行具体说明。
[0038]
本发明提供了一种x对称结构测量无人机姿态角的方法，通过三维空间x结构对称放置的6轴传感器，获取无人机各方位姿态数据，而后通过群论算法对无人机各方位姿态数据进行演算，获得无人机飞行过程中的姿态数据，实现无人机飞行控制的准确性。
[0039]
如图1所示，本发明一实例的一种x对称结构测量无人机姿态角的方法，所示无人机包括四个旋翼y1-y4，2个机臂b1-b2及其他附件，无人机系统包括两个主要模块，分别为6轴传感器模块c1-c4和群论算法模块q1。
[0040]
编号为c1-c4的6轴传感器模块，该模块设有硬件和软件两部分；硬件为6轴整合姿态获取模块如mpu6050系列等；软件主要为基于stm32的c/c++编译环境；所用的算法为姿态解算+卡尔曼滤波相结合的混合算法。
[0041]
6轴传感器模块为4个但不局限于四个，并且按照空间x机构进行对称性摆放，以无人机中心为对称心，形成体心对称结构。
[0042]
软件主要为stm32cubeide或者keil uvision5等编译软件。
[0043]
编号为q1的群论算法模块设有硬件和软件两部分；硬件主要为主频大于100mhz的stm32单片机或尺寸小于(10cm*10cm)的intel主板，主频约(1.8g-1.9ghz)；软件主要为stm32cubeide、keil uvision5、python等编译软件；所用算法主要为空间群变换、群论等融合算法。
[0044]
本发明技术实现方式如图2所示，将无人机等效为一个长方体模型，在模型中心建
立o-xyz机体坐标系；分别在长方体的对称方位放置c1-c4姿态传感器，在原点o处放置q1群论算法模块。c1-c4传感器获得的原始数据(无人机各方位姿态数据)，先通过公式(1)-(4)转换成坐标系下的数据，然后利用体心对称性特点，利用空间群和群论公式(5)-(6)，进行空间变换，从而获得在对称模型下的无人机机体姿态数据：
[0045][0046]
其中，xf为经过算法演算后的最终矩阵；x'
11-x'
13
分别为三个角度，及：翻滚角、俯仰角和巡航角，x'
21-x'
23
分别为三个方向的角速度，x'
31-x'
33
分别为三个加速度值。
[0047]
以上是本发明的较佳实施例，凡依本发明技术方案所作的改变，所产生的功能作用未超出本发明技术方案的范围时，均属于本发明的保护范围。