一种基于Nussbaum增益函数的传感器容错控制方法与流程

一种基于nussbaum增益函数的传感器容错控制方法
技术领域
1.本发明涉及传感器容错控制方法，更具体的说是一种基于nussbaum增益函数的传感器容错控制方法。


背景技术：

2.随着工业设备的越来越复杂，造成被控系统的非线性和耦合度大大提高。因此，对被控系统进行精确建模变得越来越困难。这就造成利用基于模型的控制方法实现复杂的控制任务变的非常有挑战性。因此研究不依赖系统模型得控制算法变得尤为重要。
3.其次，在设备运行中，故障的发生不可避免。为了减小或避免故障带来的严重后果，容错控制也成为了研究热点之一。现有的容错控制分为被动容错和主动容错两大类，其中主动容错由于它的自适应性和灵活性被广泛应用。但主动容错依赖于估计器的设计。
4.例如专利号201810995048.9一种基于非线性输出反馈系统的自适应一致性控制方法；
5.该专利针对一类非线性系统基于nussbaum增益函数和反步控制技术设计了一种输出反馈自适应控制方案。首先，利用滤波器对任意相对阶系统进行转换；其次，利用nussbaum函数处理未知控制方向问题；最后，引入反步控制技术设计控制器；该发明的缺点是没有考虑系统中常出现的故障问题；需要额外的引入滤波器方便控制器设计。
6.例如专利号201710551612.3一种受扰动和未知方向非线性系统的零误差跟踪控制方法；该专利针对一种含有扰动和未知控制方方向的非线性系统设计了一种控制器。首先，建议被控对象的数学模型；其次，利用nussbaum增益函数和自适应技术设计了控制器；最后，理论分析所设计的控制器可以保证系统稳定。该发明的缺点是对系统未知函数的限定条件保守性太强；此控制方案设计过程复杂。
7.上述现有技术中的容错控制方法均需要被控对象的数学模型已知，也需要设计估计器。


技术实现要素：

8.本发明的目的是提供一种基于nussbaum增益函数的传感器容错控制方法，容错控制方法不需要被控对象的数学模型已知，同时，也不用设计任何估计器。
9.本发明的目的通过以下技术方案来实现：
10.一种基于nussbaum增益函数的传感器容错控制方法，该方法包括以下步骤：
11.步骤一：给出非线性数学模型；
12.步骤二：设计容错控制器。
13.作为本技术方案的进一步优化，本发明一种基于nussbaum增益函数的传感器容错控制方法，给出非线性数学模型，可以使用以下单输入单输出严格反馈非线性系统；
[0014][0015]
其中，代表系统的状态向量，u∈r代表系统的控制输入，和分别表示系统的非线性函数，y∈r为系统的输出。
[0016]
作为本技术方案的进一步优化，本发明一种基于nussbaum增益函数的传感器容错控制方法，步骤二中利用参数分离技术把传感器故障分离。
[0017]
作为本技术方案的进一步优化，本发明一种基于nussbaum增益函数的传感器容错控制方法，传感器故障模型如下：
[0018][0019]
其中，1≥ρi＞0代表第i个状态量的效率系数，ηi≥0表示第i个状态发生的偏移故障。
[0020]
作为本技术方案的进一步优化，本发明一种基于nussbaum增益函数的传感器容错控制方法，步骤二中利用nussbaum增益函数设计容错控制方案。
[0021]
作为本技术方案的进一步优化，本发明一种基于nussbaum增益函数的传感器容错控制方法，仿真验证基于nussbaum增益函数的无模型容错控制方法的有效性。
[0022]
本发明一种基于nussbaum增益函数的传感器容错控制方法的有益效果为：
[0023]
本发明一种基于nussbaum增益函数的传感器容错控制方法，有益效果为1、提出了一种不依赖被控对象数学模型的容错控制方案；2、提出了一种不依赖任何估计器的容错控制方案；3、设计一个不依赖被控对象数学模型和估计器的容错控制方案，而且在故障发生时仍然可以很好的跟踪上参考信号。
附图说明
[0024]
下面结合附图和具体实施方法对本发明做进一步详细的说明。
[0025]
图1是本发明的参考信号随时间变化的曲线示意图；
[0026]
图2是本发明的位置信号的跟踪误差示意图；
[0027]
图3是本发明的参考信号随时间变化的曲线示意图；
[0028]
图4是本发明的位置信号的跟踪误差示意图；
[0029]
图5是本发明的参考信号随时间变化的曲线示意图；
[0030]
图6是本发明的位置信号的跟踪误差示意图；
[0031]
图7是本发明的参考信号随时间变化的曲线示意图；
[0032]
图8是本发明的角度信号的跟踪误差示意图；
[0033]
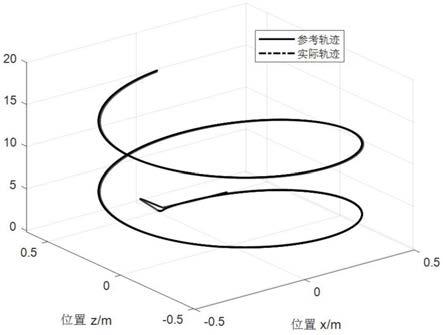
图9是本发明的四旋翼无人机的三维跟踪曲线图示意图；
[0034]
图10是本发明的控制信号随时间变化的曲线示意图一；
[0035]
图11是本发明的控制信号随时间变化的曲线示意图二；
[0036]
图12是本发明的控制信号随时间变化的曲线示意图三；
[0037]
图13是本发明的控制信号随时间变化的曲线示意图四。
具体实施方式
[0038]
下面结合附图对本发明作进一步详细说明。
[0039]
具体实施方式一：
[0040]
下面结合图1至13说明本实施方式，一种基于nussbaum增益函数的传感器容错控制方法，该方法包括以下步骤：
[0041]
步骤一：给出非线性数学模型；
[0042]
步骤二：利用参数分离技术和nussbaum增益函数设计容错控制器；
[0043]
步骤三：仿真验证基于nussbaum增益函数的传感器容错控制方法的有效性。
[0044]
具体实施方式二：
[0045]
下面结合图1至13说明本实施方式，本实施方式对实施方式一作进一步说明，给出非线性数学模型，可以使用以下单输入单输出严格反馈非线性系统；
[0046][0047]
其中，代表系统的状态向量，u∈r代表系统的控制输入，和分别表示系统的非线性函数，它们是未知的，y∈r为系统的输出。
[0048]
具体实施方式三：
[0049]
下面结合图1至13说明本实施方式，本实施方式对实施方式二作进一步说明，步骤二中利用参数分离技术把传感器故障分离。
[0050]
具体实施方式四：
[0051]
下面结合图1至13说明本实施方式，本实施方式对实施方式三作进一步说明，传感器故障模型如下：
[0052][0053]
其中，1≥ρ
i
＞0代表第i个状态量的效率系数，η
i
≥0表示第i个状态发生的偏移故障；其中，当ρ
i
＝0和η
i
＝0时，代表传感器正常，没有故障。
[0054]
具体实施方式五：
[0055]
下面结合图1至13说明本实施方式，本实施方式对实施方式四作进一步说明，步骤二中利用nussbaum增益函数设计容错控制方案。
[0056]
利用参数分离技术和nussbaum增益函数设计容错控制器
[0057]
定义系统的跟踪误差
[0058]
z
i
＝χ
i
‑
χ
id
，
ꢀꢀ
(3)
[0059]
其中i＝1，2，
…
，n,χ
1d
为系统的输出参考信号，是根据系统的控制要求事先给定的，χ
2d
，χ
3d
，
…
,χ
nd
为设计的状态参考信号，也称之为虚拟控制输入。u＝χ
n+1d
为控制输入信号。
[0060]
对公式(3)求导，并把公式(1)和(2)代入得：
[0061]
[0062]
从公式(4)中可以看出传感器故障一部分可以视为未知控制输入得变化，一部分可以视为系统未知漂移函数的变化。因此，我们利用nussbaum增益函数处理未知控制输入部分，利用反步法和障碍李雅普诺夫函数处理未知漂移函数部分。
[0063]
设计障碍李雅普诺夫函数如下：
[0064][0065]
其中λ
i
是需要设计的正常数，它代表我们希望的误差上界。对李雅普诺夫函数求导，得
[0066][0067]
利用杨氏不等式，公式(6)可以表示为
[0068][0069]
定义未知函数
[0070][0071]
则(7)可以表示为
[0072][0073]
假设是有界得，参考信号和它的导数也是有界得，那么我们可以合理得认为f
i
也是有界的，假设它的上界为设计参考信号χ
id
如下
[0074][0075]
与
[0076][0077]
其中，λ
id
和k
i
为设计的控制器参数。把公式(9)和(10)带入公式(8)得
[0078][0079]
因为在|z
i
|＜λ
i
下成立，则
[0080][0081]
其中a
i
＝k
i
，不等式两边同时积分并乘得
[0082][0083]
v
i
(0)为李雅普诺夫函数在零时刻的值。
[0084]
进一步计算得
[0085]
[0086]
假设那么由公式(5)得
[0087][0088]
也即是
[0089][0090]
整理得
[0091][0092]
所以通过设计控制器参数可以使跟踪误差可以收敛到零附近的范围内。
[0093]
具体实施方式六：
[0094]
下面结合图1至13说明本实施方式，本实施方式对实施方式五作进一步说明，仿真验证基于nussbaum增益函数的无模型容错控制方法的有效性；
[0095]
考虑以下四旋翼无人机模型：
[0096][0097]
其中，和ψ代表角度变量，x，y和z代表未知变量，u1，u2，u3和u4代表控制输入，系统参数分别为i
x
＝0.3kg/m2，i
y
＝0.03kg/m2，i
z
＝0.04kg/m2，m＝2kg，l＝1m和g＝9.8m/s2。定义中间控制变量为
[0098][0099]
则
[0100][0101]
[0102]
其中为参考信号。故障信号为
[0103][0104]
仿真结果如图1至8所示，图1为参考信号随时间变化的曲线，虚线为实际的位置信号x随时间变化的曲线；图2为位置信号的跟踪误差；图3为参考信号随时间变化的曲线，虚线为实际的位置信号y随时间变化的曲线；图4为位置信号的跟踪误差；图5为参考信号随时间变化的曲线，虚线为实际的位置信号z随时间变化的曲线；图6为位置信号的跟踪误差；图7为参考信号随时间变化的曲线，虚线为实际的角度信号ψ随时间变化的曲线；图8为角度信号的跟踪误差；可以看出本专利提出的容错控制算法不仅不依赖数学模型和估计器，而且在故障发生时仍然可以很好的跟踪上参考信号。
[0105]
当然，上述说明并非对本发明的限制，本发明也不仅限于上述举例，本技术领域的普通技术人员在本发明的实质范围内所做出的变化、改型、添加或替换，也属于本发明的保护范围。