一种欠驱动吊车微分平坦跟踪控制方法

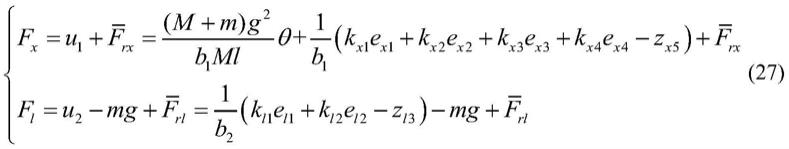
1.本发明涉及一种欠驱动吊车微分平坦跟踪控制方法，属于自动控制领域。


背景技术：

2.桥式吊车广泛应用于工厂车间、自动化码头、仓库等场所，其主要功能是实现货物快速安全的转运。在作业过程中，吊车系统存在参数摄动、风扰等不确定因素的干扰，严重影响了其防摇定位的控制效果。将货物高效、安全、准确地输运到目标位置，并抑制货物运输过程中的摆动，是目前国内外学者研究的热门问题。
3.轨迹规划对台车精准定位和负载摆动抑制起着重要作用。由于台车的起点位置默认为零，因此目标点的距离为初始位置偏差，当作业距离很长时，若不能对目标值进行平滑处理，将导致初始控制量很大，甚至难以控制。解决的方法为根据台车电机最大速度/加速度/加加速度等实际物理约束，事先规划一条先加速、再匀速、后减速的运动轨迹。因此如何设计结构简单且光滑连续，并有利于台车高效平稳运行且满足实际物理约束的参考轨迹是问题的关键。根据事先规划的平滑s型轨迹引导台车运动，并和闭环控制相结合，可以使台车运动更加平稳。对此，许多学者设计众多的闭环控制器，如滑模控制、模糊控制、模型预测、自适应控制控制等。但现有的大多数研究都是基于定绳长的基础上进行的，忽略了负载升降运动所引起的绳长变化对负载摆动的影响。在实际作业中，为提高吊车工作效率，负载升降和横向运输运动常同时进行，此时吊绳长度从定绳长转化为状态变量，绳长的变化极易引起负载的大幅摇摆，导致原有定绳长的控制方法难以取得理想的控制效果，同时绳长时变大大增强了吊车系统的欠驱动特性、非线性，增加了控制难度。
4.为解决上述所提问题，近年来国内外学者针对负载升降工况下的吊车防摆定位控制提出了许多方法。这些方法虽在一定程度上解决了变绳长桥式吊车系统的控制问题，但大都没有充分考虑摆角和位移之间的耦合关系，使其控制律中往往包含众多参数，整定困难，难以调到最优状态。由于吊车的欠驱动特性，其控制量要能实现台车准确定位及负载消摆双重目标，因此应尽可能对位移和摆角控制回路进行一体化设计，从整体上协调发挥控制系统的最大潜力。此外控制系统设计还要综合考虑系统负载质量、摩擦力、负载重心等不确定因素和环境风等外部随机扰动的影响。


技术实现要素：

5.针对上述问题和不足，本发明公布了一种欠驱动吊车微分平坦跟踪控制方法。该方法设计了包含加速、匀速、减速全过程、满足实际物理约束且光滑连续的新型加速度轨迹；将含负载升降的吊车动力学模型进行变换，得到负载横向运动和竖向运动的微分平坦输出方程，将微分平坦输出方程化成积分串联形式，设计线性扩张状态观测器估计负载横向与竖向运动的各阶状态及总和扰动；将各时刻负载横向和竖向运动各阶状态的理想值与实际值或估计值进行比较，得到状态误差，并对总和扰动进行补偿，进而构建负载横向和竖向运动的误差反馈控制律。该方法具体按以下步骤实施：
6.步骤a，对桥式吊车的动力学模型进行变换，得到负载负载横向运动和竖向运动的微分平坦输出方程：
7.包含负载升降的吊车动力学模型可描述为：
[0008][0009][0010][0011]
式中，m、m分别为台车和负载质量，x为台车位移，θ为负载摆角，l为绳长，g为重力加速度，f
x
为台车驱动力，f
l
为负载竖直方向驱动力，f
rx
，f
rl
分别表示横向和竖向运动的阻力，力，f
rx
、μ
x
、k
r
、d
l
为与摩擦力相关的系数。
[0012]
在实际情况中，负载最大摆角通常在10
°
以内，因此cosθ≈1，sinθ≈θ，θ2≈0，则式(3)可以简化为：
[0013][0014]
对原系统数学模型进行处理之后，得到近似模型：
[0015][0016][0017][0018]
式中，f
i
,i＝1,2,3分别代表各个回路的未建模部分及外界扰动组成的总和扰动。
[0019]
对摩擦力和重力项进行前馈补偿，则总控制量可表示为：
[0020][0021]
式中，为摩擦力的估计值，u1和u2分别为横向运动和竖向运动的控制量。
[0022]
考虑负载摆角θ通常在10
°
以内，负载重心坐标(x
m
，y
m
)可近似为：
[0023][0024]
式(9)对时间求二阶导数，得：
[0025][0026]
将式(10)代入式(4)并整理，得：
[0027][0028]
将式(11)代入式(9)，得：
[0029][0030]
由式(11)(12)可知，系统中所有状态变量及控制输入均可表示为(x
m
，y
m
)及其不同阶导数的代数组合形式，故吊车系统的负载运动具有平坦属性。采用x
m
的前四阶微分将负载横向运动的微分平坦输出方程表示为：
[0031][0032]
采用y
m
的前二阶微分将负载竖向运动的微分平坦输出方程表示为：
[0033][0034]
步骤b，将负载横向运动的外界干扰，系统简化而带来的模型偏差视为“总扰动”，设计五阶扩张状态观测器leso1观测负载横向运动的各阶状态及总和扰动；
[0035]
定义将系统(13)转化为如下积分串联形式：
[0036][0037]
式中，b1，d1分别为横向运动的控制量增益及总和扰动，
[0038]
根据式(15)，设计估计包含平坦输出x
m
各阶状态及总和扰动的五阶扩张状态观测器leso1:
[0039][0040]
式中，z
xi
(i＝1,
…
,5)分别为状态ξ
i
(i＝1,
…
,5)的观测值，β
xi
(i＝1,2,
…
,5)为leso1的观测器增益。
[0041]
为减少参数调整工作量，采用带宽法，将leso1增益配置在带宽ω
x
上。
[0042][0043]
求解方程(17)可得：
[0044]
[β
x1
,β
x2
,β
x3
,β
x4
,β
x5
]
t
＝[5ω
x
,10ω
x2
,10ω
x3
,5ω
x4
,ω
x5
]
t
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(18)
[0045]
步骤c，将负载竖向运动的外界干扰，系统简化而带来的模型偏差视为“总扰动”，设计三阶扩张状态观测器leso2观测负载竖向运动的各阶状态及扰动。
[0046]
为观测并补偿负载升降方向的总和扰动，定义：则系统(14)可转化为：
[0047][0048]
式中，b2，d2分别为竖向运动的控制量增益及总和扰动，b2＝1/m，
[0049]
根据式(19)，设计平坦输出y
m
各阶状态及总和扰动的扩张状态观测器leso2:
[0050][0051]
步骤d，根据点对点输运过程中先加速、后匀速、再减速的特点，及速度、加速度、加加速度约束条件，设计高阶光滑连续的加速度轨迹，作为台车运行和负载升降的参考轨迹；
[0052]
采用sigmoid函数，构造衔接点光滑连续的新型加速度轨迹，作为台车/负载的定位参考轨迹：
[0053][0054]
式中，c∈r
+
，为初始加速度调节参数，n1,n2,n3,n4∈r
+
为辅助变量，
[0055]
假定负载目标位置设定为x
d
，速度不超过v
m
，加速度不超过a
m
，加加速度不超过j
m
，确定辅助变量n1,n2,n3,n4的值：
[0056]
[0057]
该曲线全阶段连续、高阶可微，有利于台车平稳运行，同时速度、加速度、加加速度始终不超过给定的最大值，并能在最大值附近运行尽可能长的时间，有利于提高负载搬运效率。
[0058]
步骤e，根据台车和负载升降的参考加速度轨迹及负载无摆动的理想情况，确定各时刻负载横向和竖向运动的理想值，将其与负载横向和竖向运动的状态估计值进行比较，得出台车和负载各时刻的状态误差，根据状态误差设计反馈控制律；
[0059]
根据式(16)，定义负载横向运动的误差信号
[0060][0061]
式中，x
r
为负载横向运动参考轨迹表达式，根据式(21)构造。
[0062]
根据式(15)、(16)和(23)，设计负载横向运动的误差反馈控制律：
[0063][0064]
式中，k
x1
，k
x2
，k
x3
，k
x4
∈r
+
，为控制增益。
[0065]
根据式(20)，定义负载竖向运动的误差信号：
[0066][0067]
其中l
r
为负载竖向运动参考轨迹表达式，参考式(21)构造。
[0068]
根据式(19)、(20)和(25)，设计负载竖向运动的误差反馈控制律：
[0069][0070]
式中，k
l1
，k
l2
∈r
+
，为控制增益。
[0071]
根据式(8)、(24)和(26)，可得吊车系统总控制律为：
[0072][0073]
在集总大干扰下，采用式(27)所示的f
x
控制律就可使吊车在横向将吊重平稳且基本无摆地搬运到目标位置，采用式(27)所示的f
l
控制律就可在竖向将吊重平稳且基本无摆地升降到目标高度。
[0074]
本发明有益效果是：采用sigmoid函数，构造了包含加速、匀速、减速全过程且高阶光滑连续的新型加速度轨迹，该轨迹简洁、紧凑，速度、加速度、加加速度限定值明确体现在表达式中，设计方便、直观，并能使其在限定值附近运行尽可能长的时间，有利于提高运行效率。将台车运动与负载摆动进行复合，构建了负载横向和竖向运动的微分平坦输出方程，为保证平坦输出变量沿着期望参考轨迹平稳运行，设计了轨迹跟踪控制器，实现了台车位
移、负载升降及摆动的一体化控制，并引入eso补偿器对总和扰动进行估计补偿，提高了系统抵抗参数摄动、外部干扰的能力。在台车运动和负载升降的联动工况下，吊车微分平坦跟踪控制能在外界干扰情况下，使负载沿着期望轨迹快速到达目标位置，并有效抑制负载运输过程中的摆动。
附图说明
[0075]
图1为伴随负载升降的桥式吊车示意图；
[0076]
图2为新型加速度轨迹构造示意图；
[0077]
图3为存在初始摆角情况下fetc、nltc、cbc三个控制器的仿真对比，图中自上至下的5个子图分别为三个控制器控制下台车位移x(t)、负载升降l(t)、负载摆角θ(t)、台车驱动力f
x
(t)、负载升降驱动力f
l
(t)。
具体实施方式
[0078]
为使本发明的目的、技术方案和优点更加清楚明了，下面结合附图与具体实施方式，对本发明进行详细描述。
[0079]
本发明的一种欠驱动吊车微分平坦跟踪控制方法，其基本思路是：首先为使吊车系统平稳安全高效运行，选用四段具有饱和特性的sigmoid函数，设计适用于各阶段光滑连续且能满足实际物理约束的梯型加速度参考轨迹。在得到负载横向和竖向运动微分平坦输出方程的基础上，通过微分同胚变换将两方向运动方程转化为积分串联形式，进而设计微分平坦轨迹跟踪器引导台车/负载沿着期望轨迹运动，实现摆角和位移回路的一体化控制，并引入基于eso的补偿器对模型不确定性因素和外界干扰进行估计补偿，以提高其抗内/外干扰的能力，所提方法在模型参数不精确及外界干扰下都能精确定位，并抑制负载摆动，鲁棒性强。
[0080]
本发明的一种欠驱动吊车微分平坦跟踪控制方法，按照以下步骤实施：
[0081]
步骤a，对桥式吊车的动力学模型进行变换，得到负载运动状态的微分平坦输出方程
[0082]
伴随负载升降的吊车动力学模型如图1所示，其动力学方程可描述如下：
[0083][0084][0085][0086]
式中，m、m分别为台车和负载质量，x为台车位移，θ为负载摆角，l为绳长，g为重力加速度，f
x
为台车驱动力，f
l
为负载竖直方向驱动力，f
rx
，f
rl
分别表示横向和竖向运动的阻力，力，f
rx
、μ
x
、k
r
、d
l
为与摩擦力相关的系数。
[0087]
在实际情况中，负载最大摆角θ
max
通常保持在10
°
以内，因此cosθ≈1，sinθ≈θ，θ2≈0，则式(3)可以简化为：
[0088]
[0089]
对原系统数学模型进行处理之后，得到近似模型：
[0090][0091][0092][0093]
式中，f
i
,i＝1,2,3分别代表各个回路的未建模部分及外界扰动组成的总和扰动。
[0094]
对摩擦力和重力项进行前馈补偿，则总控制量可表示为：
[0095][0096]
式中，为摩擦力的估计值，u1和u2分别为横向运动和竖向运动的控制量。
[0097]
考虑负载摆角θ通常在10
°
以内，负载重心坐标(x
m
，y
m
)可近似为：
[0098][0099]
式(9)对时间求二阶导数，得：
[0100][0101]
将式(10)代入式(4)并整理，得：
[0102][0103]
将式(11)代入式(9)，得：
[0104][0105]
由式(11)(12)可知，系统中所有状态变量及控制输入均可表示为(x
m
，y
m
)及其不同阶导数的代数组合形式，故吊车系统的负载运动具有平坦属性。采用x
m
的前四阶微分将负载横向运动的微分平坦输出方程表示为：
[0106][0107]
采用y
m
的前二阶微分将负载竖向运动的微分平坦输出方程表示为：
[0108][0109]
步骤b，将负载横向运动的外界干扰，系统简化而带来的模型偏差视为“总扰动”，设计五阶扩张状态观测器leso1观测负载横向运动的各阶状态及总和扰动；
[0110]
定义将系统(13)转化为如下积分串联形式：
[0111][0112]
式中，b1，d1分别为横向运动的控制量增益及总和扰动，
[0113]
根据式(15)，设计估计包含平坦输出x
m
各阶状态及总和扰动的五阶扩张状态观测器leso1:
[0114][0115]
式中，z
xi
(i＝1,
…
,5)分别为状态ξ
i
(i＝1,
…
,5)的观测值，β
xi
(i＝1,2,
…
,5)为观测器leso1的增益。
[0116]
为减少参数调整工作量，采用带宽法，将leso1增益配置在带宽ω
x
上。
[0117][0118]
求解方程(17)可得：
[0119]
[β
x1
,β
x2
,β
x3
,β
x4
,β
x5
]
t
＝[5ω
x
,10ω
x2
,10ω
x3
,5ω
x4
,ω
x5
]
t
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(18)
[0120]
步骤c，将负载竖向运动的外界干扰，系统简化而带来的模型偏差视为“总扰动”，设计三阶扩张状态观测器leso2观测负载竖向运动的各阶状态及扰动；
[0121]
为观测并补偿负载升降方向的总和扰动，定义：则系统(14)可转化为：
[0122][0123]
式中，b2，d2分别为竖向运动的控制量增益及总和扰动，b2＝1/m，
[0124]
根据式(19)，设计平坦输出y
m
各阶状态及总和扰动的扩张状态观测器leso2:
[0125][0126]
式中，z
li
(i＝1,2,3)分别为状态δ
i
(i＝1,2,3)的观测值，β
l1
，β
l2
，β
l3
是leso2的增益。
[0127]
将leso2控制增益配置在带宽ω
l
上，即：β
l1
＝3ω
l
,
[0128]
这样leso1和leso2所有参数都变成了带宽的函数，理论上，eso带宽越大，观测器跟踪速度也越快，但同时也越容易引入噪声信号。在实际选择时，要综合考虑系统控制性能和干扰抑制等指标。
[0129]
步骤d，根据点对点输运过程中先加速、后匀速、再减速的特点，及速度、加速度、加加速度约束条件，设计高阶光滑连续的加速度轨迹，作为台车运行和负载升降的参考轨迹；
[0130]
根据吊车先加速、后匀速、再减速的点对点输运特点，采用sigmoid函数，根据图2构造衔接点光滑连续的新型加速度轨迹，作为台车/负载的定位参考轨迹：。
[0131][0132]
式中，c∈r
+
，为初始加速度调节参数，n1,n2,n3,n4∈r
+
为辅助变量，
[0133]
假定负载目标位置设定为x
d
，速度不超过v
m
，加速度不超过a
m
，加加速度不超过j
m
，根据图2对称的几何关系及sigmoid函数性质，确定辅助变量n1,n2,n3,n4的值：
[0134][0135]
该曲线全阶段连续、高阶可微，有利于台车平稳运行，同时速度、加速度、加加速度指标始终限定在给定的约束范围内，并在最大值附近运行尽可能长的时间，有利于提高负载搬运效率。
[0136]
步骤e，根据台车和负载升降的参考加速度轨迹及负载无摆动的理想情况，确定各时刻负载横向和竖向运动的理想值，将其与负载横向和竖向运动的状态估计值进行比较，得出台车和负载各时刻的状态误差，根据状态误差设计反馈控制律；
[0137]
根据式(16)，定义负载横向运动的误差信号：
[0138]
[0139]
其中，x
r
为负载横向运动参考轨迹表达式。
[0140]
根据式(15)、(16)和(23)，设计负载横向运动的误差反馈控制律：
[0141][0142]
式中，k
x1
，k
x2
，k
x3
，k
x4
∈r
+
，为控制增益。
[0143]
根据式(20)，定义负载竖向运动的误差信号：
[0144][0145]
式中，l
r
为负载竖向运动参考轨迹表达式。
[0146]
根据式(19)、(20)和(25)，设计负载竖向运动的误差反馈控制律：
[0147][0148]
式中，k
l1
，k
l2
∈r
+
，为控制增益。
[0149]
根据式(8)、(24)和(26)，得吊车系统的总控制律：
[0150][0151]
将式(24)和(26)的闭环极点分别配置在ω1，ω2，使下列特征方程λ1,λ2是hurwitz稳定的。
[0152]
λ1(s)＝s4+k
x4
s3+k
x3
s2+k
x2
s+k
x1
＝(s+ω1)4ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(28)
[0153]
λ2(s)＝s2+k
l2
s+k
l1
＝(s+ω2)2ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(29)
[0154]
计算可得控制增益的值为：
[0155][0156]
将观测器和误差反馈控制律的参数配置在带宽上，可极大减少控制器参数整定的难度。至此，基于eso补偿的微分平坦轨迹跟踪控制器已设计完毕，主要包含四个参数，通过调节两观测器带宽ω
x
，ω
l
及控制器带宽ω1，ω2，即可调节控制器性能。
[0157]
在集总大干扰下，采用式(27)所示的控制律f
x
就可使吊车在横向将吊重平稳且基本无摆地搬运到目标位置，采用式(27)所示的控制律f
l
就可在竖向将吊重平稳且基本无摆地升降到目标高度。
[0158]
定义横向运动跟踪误差为：leso1的观测误差为则横向运动的跟踪误差微分方程可表示为：
[0159][0160]
式中，
[0161][0162]
定义竖向运动跟踪误差为：ε
l1
＝l
r
‑
y
m
,eso2的观测误差为：eso2的观测误差为：则竖向运动的跟踪误差微分方程可表示为：
[0163][0164]
式中，
[0165]
闭环系统控制误差可表示为：
[0166][0167]
式中：
[0168][0169][0170]
由于两个leso的带宽分别配置在ω
x
、ω
l
上，两个控制器带宽分别配置在ω1、ω2上，因此矩阵a1、a2、e1、e2均为hurwitz稳定矩阵，在这种情况下ф矩阵也是hurwitz稳定矩阵，因此闭环系统稳定。
[0171]
步骤f、通过实验说明欠驱动吊车微分平坦跟踪控制器有效；
[0172]
为验证所提吊车微分平坦跟踪控制器(flatness based eso tracking control，fetc)的有效性，设计一仿真实验平台，吊车系统的参数设置为：m＝19.8kg，m＝1kg，g＝9.81m/s2，摩擦力参数为：f
rx
＝8.1、k
r
＝
‑
0.5、μ
x
＝0.01、d
l
＝0.7。台车初始位置x(0)＝0，目标位置x
d
＝20m，吊绳初始位置l(0)＝2m，目标位置l
d
＝10m。经参数整定，所提控制器参数选取如下：ω
x
＝15、ω
l
＝15、ω1＝5、ω2＝5。为体现所提方法的性能，将其与coupling
‑
based controller(cbc)方法和nonlinear tracking control(nltc)控制器进行对比，cbc法控制律表达式如式(34)所示，其控制参数选取为k
px
＝5、k
dx
＝7.5、k
pl
＝2、k
dl
＝2、k1＝
‑
6、n＝6，nltc法控制律表达式如式(35)所示，其控制参数选取为k
px
＝3、k
dx
＝3、k
pl
＝5、k
dl
＝5、λ
ωx
＝0.1、λ
ωl
＝0.1。考虑到落吊操作时台车定位精度和负载摆动直接影响了作业效率和操作安全性，因此仅比较落吊过程。设定台车横向运动速度、加速度、加加速度的上限分别为1m/s、
0.2m/s2、0.2m/s3，负载竖直方向速度、加速度、加加速度的上限分别为0.5m/s、0.1m/s2、0.1m/s3，初始加速度调节因子均为3.5，根据所提新型加速度轨迹nat构造台车横向运动的参考轨迹t
x
、负载竖直运动的参考轨迹t
l
，利用上述三种算法对台车横向运动、负载竖向运动进行轨迹跟踪控制，所得仿真结果如图3所示。图中从上到下曲线依次为台车位移、吊绳位置、负载摆角、台车位移方向和负载升降方向的控制量。
[0173][0174][0175]
从图3中可见，三种方法均能够较好地跟踪两条目标轨迹，且用时接近，fetc和nltc法可实现几乎无超调跟踪，而cbc法在竖向出现了跟踪超调。在消摆性能上，整个运送过程中，fetc法都可将摆角控制在2
°
以内，为三者最低，台车到达目标位置后，几乎无残摆，cbc和nltc法都难以在台车到达目标点后及时消除残余摆动，消摆时间长。fetc的控制量对时间的积分为三者最低，因此最节能。综合定位性能、消摆性能和控制力方面，本方法对吊车作业的控制效果最好。