基于事件触发机制的非线性振荡器的自适应跟踪控制方法

本发明应用于非线性系统的自适应控制，特别地涉及一种基于事件触发机制的非线性振荡器自适应输出反馈控制器设计方法。

背景技术：

传统的线性系统经过几十年的发展已经形成了较为完善的控制方案，但在实际中，许多系统(化工系统、航空航天、人工智能)并不能建模成线性系统进行处理，这些系统不可避免地包含一个或多个非线性部分。这些非线性部分的建模在精确描述系统结构地同时，也为系统控制器设计与稳定性分析带来很大的困难。另外，相比于线性系统，非线性系统种类更多样、结构更复杂，其控制方案目前为止还未能形成完整的理论体系，所以针对特定的非线性系统需要设计特定的控制方案。

在实际系统的控制中，传感器往往无法测得系统全部状态量，所以需要构造观测器估计系统状态并设计基于观测器和系统输出的控制器。普通的系统镇定问题有时无法满足实际工程的应用，更符合要求的是对系统输出的跟踪控制。此外，自适应控制作为一种控制方法，通过“以变应变”的思路广泛应用于非线性控制中，使系统在具有一定不可预测的动态特性下，仍能保持良好的性能。

另一方面，随着数字计算机的发展，采样控制系统被广泛应用于工程实践中。传统的采样控制以固定时间为周期进行采样，不可避免地会产生冗余信号。事件触发控制中，控制器采样信号的更新由设计的事件触发机制决定，能够有效地避免无用信号地传输，显然更适合于计算机控制系统，具有良好地理论与应用价值。

技术实现要素：

本发明针对现有技术的不足，提出了一种基于事件触发机制的非线性振荡器的自适应跟踪控制方法。

本发明同时考虑存在不确定扰动的情况，基于事件触发机制设计一种输出反馈控制器，该控制器通过给滑块一个自适应变化的力，使滑块位移按照给定参照信号变化，实现系统实际跟踪控制。

基于事件触发机制的非线性振荡器的自适应跟踪控制方法，该方法具体包括以下步骤：

步骤1：针对非线性振荡器，建立模型。

首先，利用力学知识建立其物理模型：

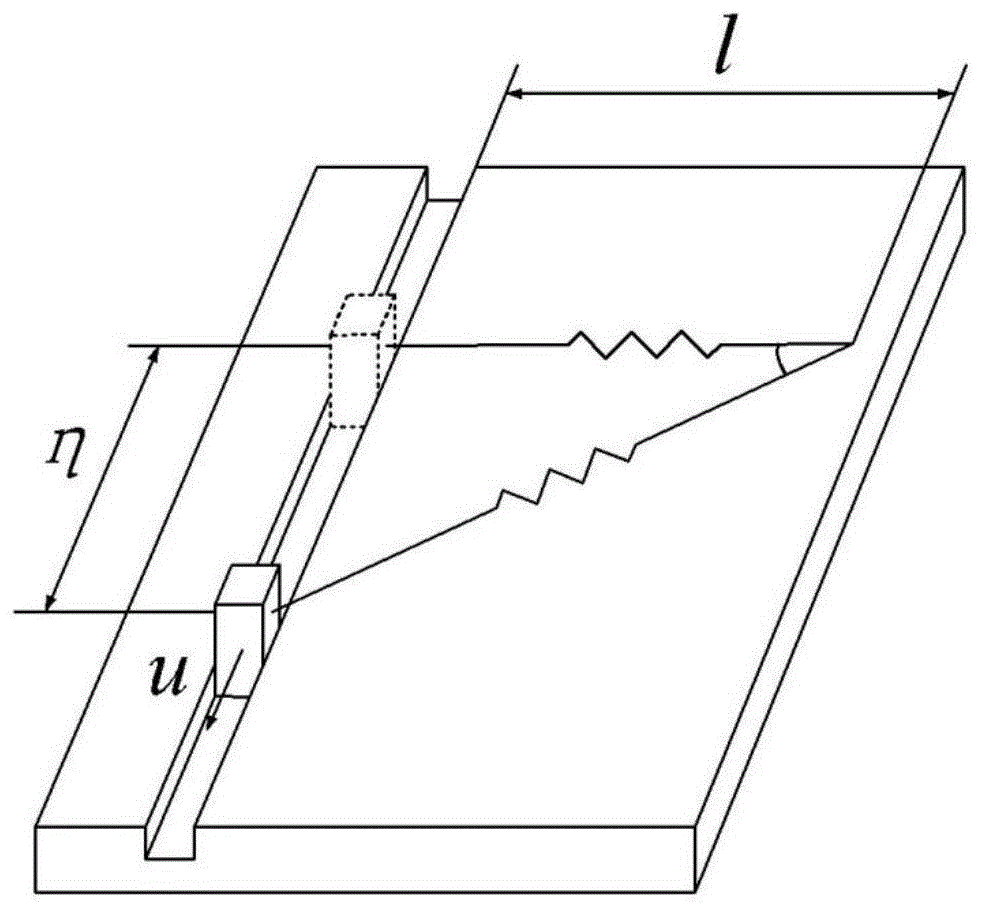
其中m代表滑块质量，代表l弹簧初始长度，k代表弹性系数，d(t)代表未知的有界时变扰动，即可能存在未知的干扰力作用在滑块上，u表示控制器给滑块施加的力。控制目标是在上述参数都未知、只有滑块位移η可测的情况下，使η跟踪上参照信号yr，且最大允许误差为λ。

定义x1＝η，系统(1)转化为如下系统学模型：

其中y表示系统的输出信号。

步骤2：控制器设计。

由于实际的振荡器系统中只有滑块位移是可测的，所以系统学模型(2)中只有y是已知的，将只利用系统输入输出信息来设计观测器重构系统状态。同时构造合适的自适应增益l，用于补偿系统不确定信息带来的影响。

式中，是系统(1)状态x＝[x1,x2]^t的估计值，ai＞0,i＝1,2是赫尔维茨多项式p(s)＝s²+a1s+a2的系数，l是自适应增益，α是待定的常数。

下面给出控制器具体结构：

其中n是可设计的常数，代表控制器触发阈值。

v(·)的定义如下：

(5)

bi＞0,i＝1,2是赫尔维茨多项式p(s)＝s²+b1s+b2的系数。

步骤4：确定控制器参数。

选择两组合适的赫尔维茨多项式系数a1＝2，a2＝1以及b1＝2，b2＝2，由引理1确定常数α＝2；

引理1：矩阵a，b和d，

因为a和b是赫尔维茨矩阵，所以存在正定矩阵p＝p^t和q＝q^t满足：

a^tp+pa≤-i,dp+pd≥αi,

b^tq+qb≤-i,dq+qd≥αi.

其中i表示二维单位矩阵；

假设最大允许跟踪误差λ＝0.1，选择参照信号yr＝0.5sint，选择控制器触发阈值n＝1。实际观测器如下：

事件触发控制器如下：

最后设定仿真对象的具体参数、初始状态和扰动信号，给出仿真结果。

本发明相对于现有技术具有的效果：

1：本发明研究的非线性振荡器模型较为复杂，已知信息较少，现有的研究结果无法给出合适的事件触发控制方案，本发明提出的控制器填充这一领域的空白。

2：本发明研究的是非线性系统跟踪控制问题，即控制滑块按照给定轨迹运动，而不是保持在某个位置不动，更能满足广泛的实际需求。

3：本发明采用的事件触发控制是一种采样控制，但相比于一般的周期采样控制能够节省计算机资源，避免了无用信号的传输，节省了计算机资源。

附图说明

图1是非线性振荡器系统实物模型；

图2是状态x1和观测器状态的轨迹图；

图3是状态x2和观测器状态的轨迹图；

图4是动态增益l的状态轨迹图；

图5是控制器u的状态轨迹图；

图6是系统输出y和参照信号yr的轨迹图；

图7是跟踪误差y-yr的轨迹图。

具体实施方式

步骤1：针对于图1中非线性振荡器，建立模型。

首先，利用力学知识建立其物理模型：

其中m代表滑块质量，代表l弹簧初始长度，k代表弹性系数，d(t)代表未知的有界时变扰动，即可能存在未知的干扰力作用在滑块上，u表示控制器给滑块施加的力。控制目标是在上述参数都未知、只有滑块位移η可测的情况下，使η跟踪上参照信号yr，且最大允许误差为λ。

定义x1＝η，系统(1)转化为如下系统学模型：

其中y表示系统的输出信号。

步骤2：控制器设计。

由于实际的振荡器系统中只有滑块位移是可测的，所以系统学模型(2)中只有y是已知的，将只利用系统输入输出信息来设计观测器重构系统状态。同时构造合适的自适应增益l，用于补偿系统不确定信息带来的影响。

式中，是系统(1)状态x＝[x1,x2]^t的估计值，ai＞0,i＝1,2是赫尔维茨多项式p(s)＝s²+a1s+a2的系数，l是动态增益，α是待定的常数。

下面给出控制器具体结构：

其中n是可设计的常数，代表控制器触发阈值。

v(·)的定义如下：

bi＞0,i＝1,2是赫尔维茨多项式p(s)＝s²+b1s+b2的系数。

步骤3：控制效果的理论分析。

引理1：矩阵a，b和d，

因为a和b是赫尔维兹矩阵，所以存在合适的系数ai和bi，i＝1,2，正定矩阵p＝p^t和q＝q^t满足：

a^tp+pa≤-i,dp+pd≥αi,

b^tq+qb≤-i,dq+qd≥αi.

其中i表示二维单位矩阵；

引入如下状态变换：

令ε＝[ε1,ε2]^t，z＝[z1,z2]^t，系统(2)和(3)表示成：

其中a，b和d如上文中定义，a＝[a1,a2]^t，

构造lyapunov函数v＝γ1ε^tpε+z^tpz，其中γ1＝4||qa||²+1。对其求导可以推出：

其中θ是一个未知常数，γ2＝θ+4m²||pc||²。

由式(8)推出l、和x是有界的，再由(3)中l的定义推出且l(t)是一致连续的。因此，由引理得：

由(3)可以进一步得到：

式(10)说明了在一段时间后跟踪误差y-yr会永远保持在区间[-λ,λ]内。

步骤4：确定控制器参数

选择两组合适的赫尔维兹多项式系数a1＝2，a2＝1以及b1＝2，b2＝2，由引理1确定一个合适的常数α＝2，假设最大允许跟踪误差λ＝0.1，选择参照信号yr＝0.5sint，选择控制器触发阈值n＝1。实际观测器如下：

以及事件触发控制器：

在给出仿真结果之前，先给出仿真对象的具体参数，需要说明的是，在设计控制器时未用到如下参数。

表1为振荡器系统的参数

表1

同时给出系统初始状态和扰动信号d(t)＝0.5cost。

图2和图3表示原系统和观测器系统状态是有界的；图4表示自适应增益是单调非减函数，并且在一段时间过后不再增长；图5表示只有当控制器达到触发阈值时才会更新控制信号；图6和图7表示系统输出在一段时间后跟踪上参照信号，并且跟踪误差小于允许误差。