一种多智能体全局一致性控制方法及系统

1.本发明涉及多智能体系统技术领域，尤其是指一种多智能体全局一致性控制方法及系统。


背景技术：

2.多智能体系统是一组自主的，相互作用的实体，它们共享一个共同的环境，利用传感器感知，并利用执行器作动。众多在实际生产实践过程中衍生的现象，都可以利用多智能体系统的相关理论去分析，诸如移动机器人的编队控制和通信网络中的一致性问题。
3.在多智能体分布式协调合作控制问题中，一致性问题作为研究多智能体集群行为的基础，具有重要的现实意义和理论价值。顾名思义，一致性问题旨在探究如何设计合适的控制策略使得每个智能体的状态随时间趋于一致。近年来，一致性问题的研究发展迅速，包括生物科学、物理科学、系统与控制科学、计算机科学等各个领域都对一致性问题从不同层面进行了深入分析。
4.到目前为止提出的譬如跟踪控制、牵制控制、脉冲控制等的控制策略，很少考虑智能体的动力学性态为非连续的情况。又考虑到实际应用环境下，控制信号的幅值必须加以限制。理论上的复杂性和实际应用的重要性促使我们进行当前的工作。本发明通过设计有效的分布式状态反馈控制器，研究了具有不连续动力学性态的多智能体系统的全局一致问题。


技术实现要素：

5.为此，本发明所要解决的技术问题在于克服现有技术中无法实现具有不连续动力学性态的多智能体系统的全局一致的缺陷，通过设计合适的分布式负反馈控制器使得各个智能体的状态随时间趋于同步，同时基于filippov微分包含和测度选择原理以及lyapunov稳定性定理，给出了多智能体系统达到全局一致的充分条件。
6.为解决上述技术问题，本发明提供了一种多智能体全局一致性控制方法，包括如下步骤：
7.确定多智能体中的参考体，并根据非线性非连续动力学函数获取各智能体状态信息的动力学方程及参考体状态信息的动力学方程；
8.根据各智能体相对参考体的误差得出受控的误差多智能体系统；
9.选择行和为零的控制配置矩阵，设计饱和分布式自适应负反馈控制器，并使控制器的时变控制增益满足自适应更新定律；
10.利用高斯误差函数和微分中值定理模拟饱和效应；
11.存在假设1：除了在可数点集非线性非连续动力学函数f(
·
)是连续可微的，并且点不属于第二类间断点，在r的紧凑区间，函数f(
·
)只有有限个跳跃间断点；
12.和假设2：当f(
·
)满足假设1，记函数f(
·
)的filippov集值映射为：
并且0∈f[f](0)，那么对于任意向量g＝[g1，g2，
…
，g
n
]
t
，d＝[d1，d2，
…
，d
n
]
t
∈r
n
，存在两个正的常数q和m，使得
[0013]
sup|φ
‑
χ|≤q|g
‑
d|+m......(13)
[0014]
成立，其中，
[0015]
并且f[f
i
](z
i
)＝[min{f
‑
(z
i
)，f
+
(z
i
)}，max{f
‑
(z
i
)，f
+
(z
i
)}]；
[0016]
在饱和分布式自适应负反馈控制器和自适应更新定律作用下，基于filippov微分包含和测度选择原理以及lyapunov稳定性定理，结合假设1和假设2，得出多智能体系统达到全局一致的充分条件。
[0017]
在本发明的一个实施例中，各智能体的动力学方程为：
[0018][0019]
其中，表示第i个智能体的状态变量，f(
·
)：r
n
→
r
n
是一个非线性非连续的向量值函数；
[0020]
参考体的动力学方程为：
[0021][0022]
其中，
[0023]
在本发明的一个实施例中，非线性非连续动力学函数选择为f(z)＝0.1z+0.3sign(z)，得出q＝0.1，m＝0.6。
[0024]
在本发明的一个实施例中，饱和分布式自适应负反馈控制器为：
[0025][0026]
其中，a＝[a
ij
]
n
×
n
是控制配置矩阵，满足误差向量ρ表示一个正的常数，sign(
·
)表示符号函数，k
i
(t)表示时变控制增益，控制向量
[0027]
在本发明的一个实施例中，若第i个智能体与第j个智能体(i≠j)之间有信息传递，则a
ij
＝a
ji
＞0，否则a
ij
＝a
ji
＝0，sat(
·
)表示饱和函数，定义如下：
[0028][0029]
其中，是自定义控制器阈值。
[0030]
在本发明的一个实施例中，针对时变控制增益k
i
(t)，自适应更新定律如下：
[0031]
[0032]
其中β＞0，i＝1，2，
…
，n。
[0033]
在本发明的一个实施例中，应用高斯误差函数和微分中值定理模拟饱和效应得到：
[0034][0035]
其中，是有界的，diag[
·
]表示对角矩阵。
[0036]
在本发明的一个实施例中，多智能体系统达到全局一致的充分条件为存在正的常数m，p，ρ，β满足如下不等式组：
[0037][0038]
其中，分别表示矩阵g(ξ
i
)的最小和最大特征值，控制增益矩阵k＝diag[k1，k2，
…
，k
n
]。
[0039]
在本发明的一个实施例中，在得到多智能体系统达到全局一致的充分条件后，通过搭建模型，得出仿真结果验证条件。
[0040]
一种多智能体全局一致性控制系统，包括：
[0041]
获取模块，用于根据上述的智能体和参考体的动力学方程获取各个智能体的状态信息和参考体的状态信息；
[0042]
建模模块，用于建立误差模型；
[0043]
饱和分布式自适应负反馈控制器，用于使得各个智能体的状态随时间趋于同步；
[0044]
模拟模块，用于模拟饱和效应；
[0045]
目标函数确定模块，用于基于filippov微分包含和测度选择原理以及lyapunov稳定性定理得到控制策略的目标函数；
[0046]
控制模块，用于以目标函数为控制目标，按照饱和分布式自适应负反馈控制器和自适应更新定律，对各个智能体进行控制。
[0047]
本发明的上述技术方案相比现有技术具有以下优点：
[0048]
本发明通过设计合适的饱和分布式自适应负反馈控制器使得各个智能体的状态随时间趋于同步；
[0049]
本发明基于filippov微分包含和测度选择原理以及lyapunov稳定性定理，给出了非线性非连续动力学性态的多智能体系统达到全局一致的充分条件，由于实际工程应用环境下，存在大量不连续的系统，本发明考虑的非线性非连续动力学性态的多智能体系统模型更具有普适性和现实意义；
[0050]
利用高斯误差函数和微分中值定理，来近似模拟饱和效应，方便后续控制器的设计。
附图说明
[0051]
为了使本发明的内容更容易被清楚的理解，下面根据本发明的具体实施例并结合
附图，对本发明作进一步详细的说明，其中
[0052]
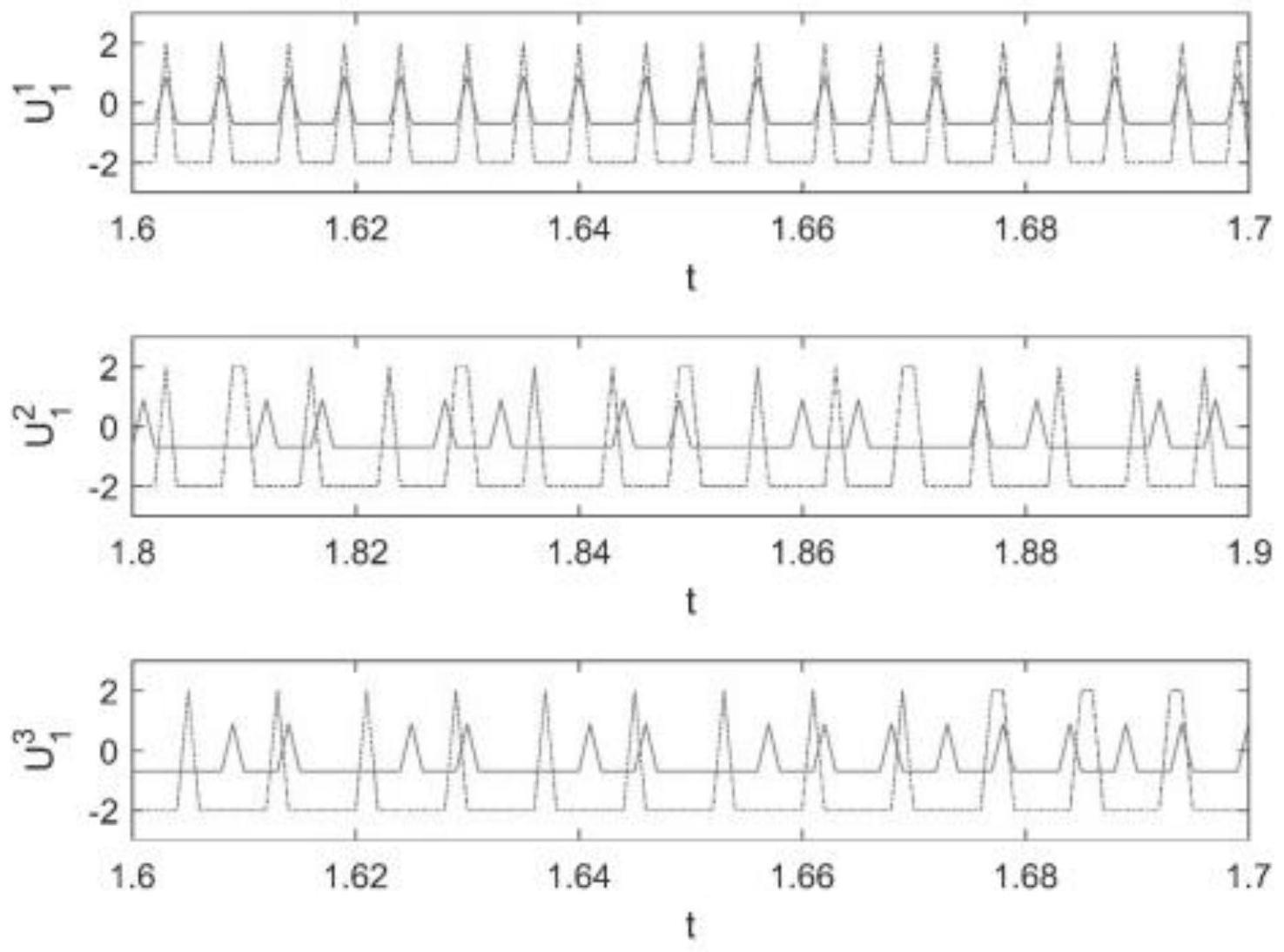
图1是本发明控制器u1(t)的原始输出和通过高斯误差函数和微分中值定理近似模拟的饱和输出；
[0053]
图2是本发明控制器u1(t)的原始输出和仅通过高斯误差函数近似模拟的饱和输出；
[0054]
图3是本发明每个智能体的状态与目标状态之间的一致性误差
[0055]
图4是本发明反馈控制增益k
i
(t)的演变图。
具体实施方式
[0056]
下面结合附图和具体实施例对本发明作进一步说明，以使本领域的技术人员可以更好地理解本发明并能予以实施，但所举实施例不作为对本发明的限定。
[0057]
本发明的一种多智能体全局一致性控制方法，包括如下步骤：
[0058]
确定多智能体中的参考体，并根据非线性非连续动力学函数获取各智能体状态信息的动力学方程及参考体状态信息的动力学方程。具体的，建立非连续非线性的多智能体系统并确定其一致性目标：
[0059][0060]
其中，表示第i个智能体的状态变量，f(
·
)：r
n
→
r
n
是一个非线性非连续的向量值函数。
[0061]
全局一致，是多智能体系统的一种特殊集群行为，指各个智能体的状态都随时间趋于一致，基于此我们将某个孤立智能体的动力学状态作为参考体，即一致性目标，当系统中的所有智能体状态都与之同步时，则多智能体系统达到全局一致。在本实施例中，我们考虑如下孤立智能体作为一致性目标，即参考体的动力学方程为：
[0062][0063]
其中，
[0064]
本实施例中通过传感器装置获得各节点状态信息，即参考体和各智能体的状态信息，同时以参考体的状态为参考，确定智能体与参考体之间的误差，建立误差模型，可以定义误差向量为：根据各智能体相对参考体的误差，再由(1)和(2)得出受控的误差多智能体系统：
[0065][0066]
其中i＝1，2，
…
，n。
[0067]
要实现多智能体系统的全局一致同步，需要向每个智能体传输邻接节点与参考节点的状态信息，因此本实施例中设计饱和分布式自适应负反馈控制器：
[0068]
[0069]
其中，a＝[a
ij
]
n
×
n
是控制配置矩阵，满足行和为零，即ρ表示一个正的常数，sign(
·
)表示符号函数，k
i
(t)表示时变控制增益，控制向量
[0070]
若第i个智能体与第j个智能体(i≠j)之间有信息传递，则a
ij
＝a
ji
＞0，否则a
ij
＝a
ji
＝0，sat(
·
)表示饱和函数，考虑到系统实际工况和运行成本，对于控制信号有必要加以限制，因此定义如下：
[0071][0072]
其中，i＝1，2，
…
，n，j＝1，2，
…
，n是自定义控制器阈值，即通过设计饱和策略对控制器的输出设定阈值。
[0073]
进一步的，为了获得合适的控制器增益，针对时变控制增益k
i
(t)，自适应更新定律如下：
[0074][0075]
其中β＞0，i＝1，2，
…
，n。
[0076]
更进一步的，本实施例中，为了处理控制器的饱和效应(5)，引入高斯误差函数的概念，这可以近似平滑控制信号在饱和效应作用下的非线性。定义如下：
[0077][0078]
其中erf(
·
)表示高斯误差函数，形式为
[0079]
为了简化后续控制器的设计，应用高斯误差函数和微分中值定理来模拟饱和效应(5)，定义如下函数：
[0080][0081]
其中是有界的，这表明||
·
||表示2
‑
范数。
[0082]
根据微分中值定理，存在一个常数满足以下等式：
[0083][0084]
其中，
[0085]
考虑到g(0)＝0，选择u
i0
＝0，可以将(9)式转换成：
[0086][0087]
根据(8)和(9)，我们可以得到：
[0088][0089]
由此可以得到下式：
[0090][0091]
其中，diag[
·
]表示对角矩阵。
[0092]
引入假设条件，包括假设1：除了在可数点集非线性非连续动力学函数f(
·
)是连续可微的，并且点不属于第二类间断点，在r的紧凑区间，函数f(
·
)只有有限个跳跃间断点；
[0093]
和假设2：当f(
·
)满足假设1，记函数f(
·
)的filippov集值映射为：并且0∈f[f](0)，那么对于任意向量g＝[g1，g2，
…
，g
n
]
t
，d＝[d1，d2，
…
，d
n
]
t
∈r
n
，存在两个正的常数q和m，使得下式成立：
[0094]
sup|φ
‑
χ|≤q|g
‑
d|+m......(13)
[0095]
成立，其中，
[0096]
并且f[f
i
](z
i
)＝[min{f
‑
(z
i
)，f
+
(z
i
)}，max{f
‑
(z
i
)，f
+
(z
i
)}]。
[0097]
在饱和分布式自适应负反馈控制器和自适应更新定律作用下，基于filippov微分包含和测度选择原理以及lyapunov稳定性定理，结合假设1和假设2，得出多智能体系统达到全局一致的充分条件。
[0098]
选取如下lyapunov函数：
[0099][0100]
计算v(t)关于时间t的集值lie导数l
e
(v(t))，并根据filippov集值映射的性质可得：
[0101][0102]
根据filippov测度选择定理选取函数和其中t∈[0，t]，结合假设2可得：
[0103][0104][0105]
接着可以得到：
[0106][0107]
然后进一步计算得：
[0108][0109][0110][0111][0112]
其中表示反馈增益矩阵。
[0113]
综合以及(17)可以得到：
[0114][0115]
由此便可得出该控制策略下多智能体系统达到全局一致同步的充分条件。
[0116]
若结论成立，多智能体系统达到全局一致的充分条件为存在正的常数m，p，ρ，β满足如下不等式组：
[0117][0118]
其中，分别表示矩阵g(ξ
i
)的最小和最大特征值，控制增益矩阵k＝diag[k1，k2，
…
，k
n
]。在饱和分布式自适应负反馈控制器(4)和自适应更新定律(6)的作用下多智能体系统(1)能到达全局一致。
[0119]
参照图1
‑
图4，为本实施例仿真计算的结果。本实施例中，非线性非连续动力学函数选择为f(z)＝0.1z+0.3sign(z)，计算得出q＝0.1，m＝0.6。为尽量模拟实际工业环境，选择四个智能体构成多智能体系统。为了对其施加分布式控制，选择以下控制耦合矩阵a：
[0120][0121]
为了限制控制器的输出，利用高斯误差函数和微分中值定理近似模拟饱和效应。选择g(ξ1)＝g(ξ2)＝g(ξ3)＝g(ξ4)＝diag[0.4，0.5，0.6]，挑选去近似补偿每个控制器的真实饱和与模拟饱和输出之间的误差。容易得到
[0122]
根据本发明多智能体系统达到全局一致的充分条件，计算出参数β，ρ、c的具体数值。本实施例中使用lmi工具箱进行计算。
[0123]
在得到多智能体系统达到全局一致的充分条件后，通过搭建模型，得出仿真结果验证条件。本实施例中搭建simulink模型，得到仿真结果。通过图4可知，各个智能体状态在满足所提出的条件下达到了全局一致同步。
[0124]
本发明的一种多智能体全局一致性控制系统，包括：
[0125]
获取模块，用于根据上述智能体和参考体的动力学方程获取各个智能体的状态信息和参考体的状态信息；本实施例中，非线性非连续动力学函数选择为f(
·
)，各智能体位置函数为：参考体位置函数为：
[0126]
建模模块，用于建立误差模型；误差向量为：受控的误差多智能体系统为
[0127]
饱和分布式负反馈控制器，用于使得各个智能体的状态随时间趋于同步；饱和分布式自适应负反馈控制器为：
[0128][0129]
模拟模块，用于应用高斯误差函数和微分中值定理来模拟饱和效应；
[0130]
目标函数确定模块，用于基于filippov微分包含和测度选择原理以及lyapunov稳定性定理得到控制策略的目标函数；即多智能体系统达到全局一致的充分条件为存在正的常数m，p，ρ，β满足如下不等式组：
[0131][0132]
控制模块，用于以目标函数为控制目标，按照饱和分布式自适应负反馈控制器和自适应更新定律，对各个智能体进行控制，使各个智能体状态在满足所提出的条件下达到了全局一致同步。
[0133]
显然，上述实施例仅仅是为清楚地说明所作的举例，并非对实施方式的限定。对于所属领域的普通技术人员来说，在上述说明的基础上还可以做出其它不同形式变化或变动。这里无需也无法对所有的实施方式予以穷举。而由此所引伸出的显而易见的变化或变动仍处于本发明创造的保护范围之中。