一种基于时间同步的多轴协同控制方法

本发明涉及多轴控制的技术领域，具体涉及一种基于时间同步的多轴协同控制方法。

背景技术：

近年来，随着工业领域产品工艺要求的不断提高，以及生产规模的激增，为了得到更高的加工精度，生产制造阶段各子系统之间协同作用的重要性格外突显，在多轴运动控制中，人们一直致力于得到更高的运动控制精度，使得每个轴的实际运动可以比较准确地跟踪输入信号，然而由于伺服系统本身的延时、机械结构不可避免的摩擦以及传动系统的反向间隙问题，精确地跟踪规划路径以得到高精度轨迹依然存在着有待解决的问题，多轴协同控制技术作为一门跨学科的综合性技术，其在多机器人系统协调控制、航空航天、无轴传动印刷机伺服系统的协同控制、数控系统位置控制等多变量控制领域中得到了广泛的应用，解决了很多实际的工程问题，保证了生产线的高效、稳定运行，给社会经济发展带来了巨大的效益，作为多轴协同控制的关键技术之一，协同控制方法的发展随着控制结构的发展而发展。

一般的，采用一个电机控制一个轴，实现多轴同步控制即转化为多电机同步控制算法，多电机协同控制算法可大致分为两类，一种是经典算法，另一种智能算法，经典算法包括pid算法等，智能控制算法有神经网络控制，模糊控制，滑模变结构控制等。

pid算法，即比例-积分-微分控制，是目前为止工业控制领域最为常见也是发展最为成熟的一类控制方式，此算法主要适用于线性非时变系统，算法简单成本低结构易于实现且能消除稳态误差；智能控制算法可针对控制对象的环境、目标和任务的不确定性和复杂性提供解决方案，具有良好的自适应能力，鲁棒性好，适用于时变和欸线性系统，但它的自调整能力差，对非线性、强耦合系统的控制效果不理想；神经网络算法主要应用于多变量、非线性以及各种复杂不确定性系统，尤其在多输入输出系统中表现优异，是目前比较火热的智能控制算法之一，神经网络的优点是具有较强的自主学习和非线性逼近能力，缺点是网络权值的获取需要对大量的数据进行训练，在经济投入有限或者系统实时性要求较高的情况下，神经网络算法局限性较大；模糊算法是一种以模糊集合论、模糊语言变量和模糊逻辑推理为数学基础的智能控制方法，但是将一个用于较为复杂的不确定系统中时，得到的精度会比较低，调节时间也比较长；滑模控制以其对参数变化及扰动不敏感、鲁棒性强、响应速度快等优点，在电机调速系统得到了广泛的应用，但是，它的开关特性在保证了系统鲁棒性的同时，也导致了输出抖振现象。

pid算法的调节效果依赖于被控对象的数学模型，只有在模型准确并且模型参数恒定的情况下才能获得理想的控制效果，且对非线性强耦合的系统控制效果不佳，而多直线电机伺服系统是一个非线性、时变复杂系统，建立起精确的数学模型是非常困难的，且在运行过程中当系统状态改变时，pid控制器参数无法做出相应的调整，故采用传统的pid控制效果会变差；智能协同控制算法普遍的不足在于，智能算法的运算时间会随着协同运动轴数量的增加而增大，一旦算法出现漏洞或者运算死区，极易造成系统的不稳定，因此对智能算法的探索及其实际工程应用还需要更多深入的研究，此外，以上两类控制算法皆需要设计独立的控制器硬件，当设备硬件条件无法改变时，控制算法的实现具有一定的难度。

技术实现要素：

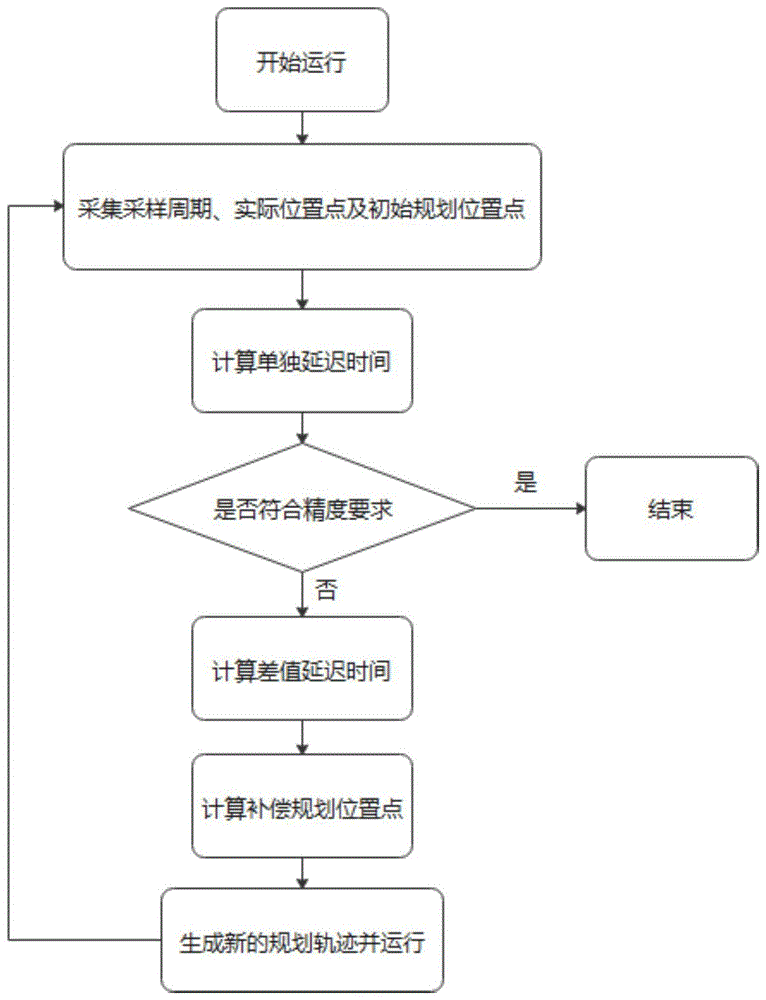
为了解决上述技术问题，本发明的目的在于提供一种基于时间同步的多轴协同控制方法，其包括步骤1：开始运行；步骤2：采集采样周期、实际位置点及初始规划位置点；步骤3：计算单独延迟时间；步骤4：若符合精度要求，则结束，否则进入步骤5；步骤5：计算差值延迟时间；步骤6：计算补偿规划位置点；步骤7：将补偿规划位置点生产新的规划轨迹并运行，返回步骤2；该基于时间同步的多轴协同控制方法具有提高控制精度、可移植性良好、多轴耦合关系不复杂、控制结构简单、抗干扰性好的优点。

为实现上述发明目的，本发明采取的技术方案如下：

一种基于时间同步的多轴协同控制方法，包括以下步骤：

步骤1：n个轴开始运行初始规划轨迹，n为大于或等于2的正整数；

步骤2：利用数据采样模块采集n个轴的采样周期以及每个时刻的实际位置点、初始规划位置点，记t为采样周期，pk，i为第i轴kt时刻的初始规划位置点，qk，i为第i轴kt时刻的实际位置点，i＝1、2、3、……、n；

步骤3：计算n个轴的单独延迟时间δtk，i；

步骤4：计算n个轴的运动是否符合精度要求，若符合，则结束，否则进入步骤5；

步骤5：获取最小单独延迟时间，n个轴的单独延迟时间分别与最小单独延迟时间之差得到n个轴的差值延迟时间；

步骤6：计算n个轴在差值延迟时间点的补偿规划位置点；

步骤7：将所有补偿规划位置点生成新的规划轨迹并运行，返回步骤2。

作为优选，步骤3包括以下步骤：

步骤3.1：找到实际位置点qk，i所在的区间计算规划位置点与规划位置点之间的距离并记为lk，i；

步骤3.2：计算实际位置点qk，i与规划位置点之间的距离为lk，i；

步骤3.3，计算pk，i的单独延迟时间δtk，i，

作为优选，在步骤3.1中，以p0，i作为原点，若或则qk，i落在区间

作为优选，在步骤4中，若n个轴的单独延迟时间δtk，i均小于设定的阈值时，则结束，否则进入步骤5，通过这样设置，当n个轴的单独延迟时间δtk，i均小于设定的阈值时，表明n个轴的运动均达到精度要求，则结束，否则进入步骤5，通过n个轴的单独延迟时间δtk，i与阈值进行对比检验多轴的控制精度，便于检验，且适用性广。

作为优选，在步骤5中，找到单独延迟时间δtk，i中最小单独延迟时间，并记δtmin为最小单独延迟时间，记为差值延迟时间，

作为优选，在步骤6中，记为补偿规划位置点，

相对于现有技术，本发明取得了有益的技术效果：

采用本发明的多轴协同控制方法，可以在不改变已有硬件的条件下，只通过对规划位置点的改良，在同一时刻下，把其余单轴延迟时间相对大的点同步到单轴延迟时间最小的点，对规划轨迹进行多次迭代学习，得到精确度较高的多轴协同效果，由于不涉及硬件条件的改良，本发明的多轴协同控制方法具有良好的可移植性，可以应用于多个涉及多轴控制的场景和设备，另外，本发明的多轴耦合关系并不复杂，控制结构简单，抗干扰性好，较好的解决多轴协同控制问题，从整体上提高控制精度。

附图说明

图1是本发明实施例1多轴协同控制方法的流程图；

图2是本发明实施例1计算单独延迟时间的示意图；

图3是本发明实施例1三轴系统的单独延迟时间的示意图；

图4是本发明实施例1计算补偿规划位置点的示意图；

图5是本发明实施例1三轴系统的补偿规划位置点的示意图；

图6是本发明实施例2规划轮廓与实际轮廓的示意图；

图7是本发明实施例2规划轮廓点作垂线三种情况的示意图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合实施例对本发明进行进一步详细说明，但本发明要求保护的范围并不局限于下述具体实施例。

实施例1：

参考图1-5，本实施例公开了一种基于时间同步的多轴协同控制方法，适用于直线运动或旋转运动或直线与旋转运功组合的多轴控制设备，比如机器人、数控机床以及印刷机等需要多个轴运动配合进行工作的系统，多轴协同控制方法包括以下步骤：

步骤1：n个轴开始运行初始规划轨迹，n为大于或等于2的正整数；

步骤2：利用数据采样模块采集n个轴的采样周期以及每个时刻的实际位置点、初始规划位置点，记t为采样周期，pk，i为第i轴kt时刻的初始规划位置点，qk，i为第i轴kt时刻的实际位置点，i＝1、2、3、……、n；

步骤3：计算n个轴的单独延迟时间δtk，i；

步骤4：计算n个轴的运动是否符合精度要求，若符合，则结束，否则进入步骤5；

步骤5：获取最小单独延迟时间，n个轴的单独延迟时间分别与最小单独延迟时间之差得到n个轴的差值延迟时间；

步骤6：计算n个轴在差值延迟时间点的补偿规划位置点；

步骤7：将所有补偿规划位置点生成新的规划轨迹并运行，返回步骤2。

采用本发明的多轴协同控制方法，可以在不改变已有硬件的条件下，只通过对规划位置点的改良，在同一时刻下，把其余单轴延迟时间相对大的点同步到单轴延迟时间最小的点，对规划轨迹进行多次迭代学习，得到精确度较高的多轴协同效果，由于不涉及硬件条件的改良，本发明的多轴协同控制方法具有良好的可移植性，可以应用于多个涉及多轴控制的场景和设备，另外，本发明的多轴耦合关系并不复杂，控制结构简单，抗干扰性好，较好的解决多轴协同控制问题，从整体上提高控制精度。

步骤3包括以下步骤：

步骤3.1：找到实际位置点qk，i所在的区间计算规划位置点与规划位置点之间的距离并记为lk，i；

步骤3.2：计算实际位置点qk，i与规划位置点之间的距离为lk，i；

步骤3.3，参考图2，计算pk，i的单独延迟时间δtk，i，当采样间隔t足够小时，相邻的两个规划位置点pk，i之间的轨迹接近直线，因此上述同样适用于旋转运动控制，此时δtk，i≥0；

举三轴系统为例，参考图3，

第一轴第kt时刻的单独延迟时间为

第二轴第kt时刻的单独延迟时间为

第三轴第kt时刻的单独延迟时间为

在步骤3.1中，以p0，i作为原点，若或则qk，i落在区间

在步骤4中，若n个轴的单独延迟时间δtk，i均小于设定的阈值时，阈值根据实际精度要求设定，此时表明对n个轴的控制精度均符合精度要求，则结束，否则进入步骤5，即存在至少一个轴的单独延迟时间δtk，i大于设定的阈值时，表明存在至少一个轴的控制精度不符合精度要求，进入步骤5，通过n个轴的单独延迟时间δtk，i与阈值进行对比检验多轴的控制精度，便于检验，且适用性广；

在步骤5中，找到单独延迟时间δtk，i的最小单独延迟时间，并记δtmin为最小单独延迟时间，记为差值延迟时间，

举三轴系统为例，若δtk，1<δtk，2<δtk，3，则δtmin＝δtk，1；

第一轴第kt时刻的差值延迟时间

第二轴第kt时刻的差值延迟时间

第三轴第kt时刻的差值延迟时间

参考图4，在步骤6中，记为补偿规划位置点，将所有的补偿规划点生成新的规划轨迹。

举三轴系统为例，参考下图5，

第一轴第kt时刻的新的补偿规划位置点

第二轴第kt时刻的新的补偿规划位置点

第三轴第kt时刻的新的补偿规划位置点

实施例2：

本实施例仅描述与实施例1的区别技术特征，其余技术特征均与实施例1相同，本实施例提供另一种判断是否符合精度要求的方法，本实施例中，在步骤2中，记pk为多轴协同kt时刻的规划轮廓点，qk为多轴协同kt时刻的实际轮廓点。

参考图6-7，在步骤4中，计算实际轮廓与规划轮廓之间是否符合精度要求，若符合，则结束，否则进入步骤5，具体的，步骤4包括以下步骤：

步骤4.1：寻找与kt时刻的规划轮廓点pk距离最近的实际轮廓点qk+j；

步骤4.2：计算规划轮廓点pk与实际轮廓点qk+j之间的轮廓误差e，若轮廓误差e均小于设定阈值时，则结束，否则进入步骤5。

进一步的，在步骤4.1中，记dk，j为规划轮廓点pk与实际轮廓点qk+j之间的距离，j为整数，

找到最小值的dk，j，对应的实际轮廓点qk+j与规划轮廓点pk的距离最近，比如当dk，1为最小值时，实际轮廓点qk+1与规划轮廓点pk的距离最近。

在步骤4.2中，将qk+j分别与在qk+j前后的实际轮廓点qk+j-1及qk+j+1进行连线，得到两条线段分别为h1及h2，并从pk分别向两条线段h1及h2作垂线，垂足分别为c1及c2；

参考图7(1)，若垂足c1及c2分别在线段h1及h2上时，轮廓误差e＝min{|pkc1|，|pkc2|}，min{|pkc1|，|pkc2|}的意思是指|pkc1|与|pkc2|两者之间的最小值；

参考图7(2)，若垂足c1在线段h1上，垂足c2不在线段h2上时，即垂足c2在线段h2的延长线上时，轮廓误差e＝|pkc1|；

若垂足c2在线段h2上，垂足c1不在线段h1上时，即垂足c1在线段h1的延长线上时，轮廓误差e＝|pkc2|；

参考图7(3)，若垂足c1及c2均不在线段h1及h2上时，即垂足c1及c2分别在线段h1及h2的延长线上时，轮廓误差e＝|pkqk+j|。

根据上述说明书的揭示和教导，本发明所属领域的技术人员还可以对上述实施方式进行变更和修改。因此，本发明并不局限于上面揭示和描述的具体实施方式，对发明的一些修改和变更也应当落入本发明的权利要求的保护范围内。此外，尽管本说明书中使用了一些特定的术语，但这些术语只是为了方便说明，并不对发明构成任何限制。