一种比例积分滑模面的数控机床用模糊滑模位置控制方法与流程

本发明涉及一种比例积分滑模面的数控机床用模糊滑模位置控制方法，属于机械数控机床位置控制领域。

背景技术：

机械数控机床是制造业的基础，国家发展振兴的战略基础，而数控装置是数控机床中的核心组成部分，决定数控机床的功能和性能。随着制造业的蓬勃发展，对数控装置的技术指标、综合性能以及可靠性等方面提出了更高的要求，同时也促进了数控装置技术指标和综合性能监测水平的发展。在国家大力发展国产数控装置的发展和数控装置的研发的背景下，迫切的需要提升数控装置的控制性能。

在数控装置中控制系统易出现故障，导致故障的主要原因是数控系统中电机及齿轮自身的非线性特性，致使系统自身参数值发生偏移，从而导致加工出来的工件精度低，无法使用。

技术实现要素：

针对上述现有技术存在的问题，本发明提供一种比例积分滑模面的数控机床用模糊滑模位置控制方法，将具有比例积分的滑模面的模糊滑模控制应用于机械数控机床位置控制中，提升加工精度，消除人为失误对产品质量的影响，改善生产条件，提高工业生产效率。

为了实现上述目的，本发明采用的技术方案是：一种比例积分滑模面的数控机床用模糊滑模位置控制方法，包括以下步骤；

步骤一：首先机械数控机床非线性系统进行分析，提取机械数控机床位置的实际反馈值θ，得到与机械数控机床的位置期望值θd的位置误差e(t)；

步骤二：设计比例积分滑模面切换函数，将滑模控制中的切换函数s(t)作为模糊系统的输入；

步骤三：对模糊控制器进行设计，包括根据经验构造模糊规则库，大大减少模糊规则的数量；采用重心算法，将系统进行反模糊化，得到模糊控制器输出u(t)；

步骤四：将机械数控机床位置控制器的位置输出信号u(t)输入数控系统，机械数控机床系统输出的位置角度反馈至输入端。

优选的，所述步骤一中的位置误差e(t)计算方法为：

根据系统的输入与输出数据为依据辨识控制系统的结构、参数与模型，以此得到的位置伺服系统模型，模型表达式为：

θ(k)＝f[θ(k-1)，θ(k-2)，…θ(k-n)，θd(k-1)，θd(k-2)，…θd(k-m)](1)

式中，θ为系统位置角度输出；θd为系统位置角度指令输入；n为系统阶次；m为输出阶次；k为位置环参数；

同时进行时间序列离散化处理，得到式(1)的差分方程表达式：

式中，ai与bj均为辨识的模型参数，其中i为[1，n]中的整数，j为[1，m]为中的整数；

通过上述的模型结构、参数进行辨识，可将网格搜索算法和递推最小二乘法进行结合辨识控制系统的模型结构与参数最终可得到机械数控机床位置伺服系统的数学模型；机械数控机床控制位置角度可表示为：

式中，f和g为机械数控机床中未知的非线性函数；d(t)为机械数控机床运行过程中所受到的干扰，跟踪误差为：

e(t)＝θ(t)-θd(t)(4)

式中，θ为系统位置角度输出；θd为系统位置角度指令输入。

优选的，所述步骤二中的比例积分滑模面切换函数为：

式中，k为非零常数，k1和k2为非零正常数；

当滑模控制处于理想状态，则表现为:

通过确定k1和k2，跟踪误差e(t)及其导数趋近于零；相比于机械数控机床传统的pid控制器而言，可以采用切换函数s(t)作为模糊控制器的输入，控制输入u(t)作为模糊系统的输出，构成一个单输入-单输出(siso)模糊系统。

优选的，所述步骤三中的模糊控制器设计方法为：

模糊控制器为系统的重要部分，以模糊数学作为理论支柱；首先将机械数控机床切刀的位置控制量的比例积分滑模面切换函数s(t)，作为模糊输入(其中通过对应的模糊语言来具体描述)，此后依照与经验设计的模糊关系对模糊控制器的控制规则进行设计；最后，依据推理得到的控制规则开展模糊决策机制，由此获取模糊控制量u(t)；

该模糊控制器的模糊规则形式为：

rulei:ifsisfsⁱthenuisai(8)

式中，fsⁱ和ai(i＝1，2，，m)分别为输入和输出的模糊集合；

根据专家经验可在在模糊控制系统中建立如下5条模糊规则：

(6)if(sisnb)then(uispb)

(7)if(sisns)then(uisps)

(8)if(sisz)then(uisz)

(9)if(sisps)then(uisns)

(10)if(sispb)then(uisnb)

其中s和u的隶属函数采用“负大”(nb)、“负小(ns)”、“零(z)”、“正小(pb)”、“正大(pb)”。其模糊定义规则为：若s为nb(负大)，则u为ps(正大)；若s为ns(负小)，则u为ps(正小)；若s为z(零)，则u为z(零)；若s为ps(正小)，则u为ns(正小)；若s为pb(负大)，则u为nb(负大)；

最后，依据得到的控制规则开展模糊决策机制；重心法是取隶属度函数曲线与横坐标围成面积的重心作为模糊推理的最终输出值；采用重心法进行反模糊化，得到控制器输出为：

式中，ωi为第i条规则中前提的隶属度，ai为第i条规则中结论的隶属度。

优选的，所述步骤四中将机械数控机床位置控制器的位置输出信号u(t)输入数控系统，机械数控机床系统输出的位置角度反馈至输入端，实现位置速度双闭环控制。

本发明的有益效果是：本发明运用比例积分滑模面的位置控制方法替代传统机械数控机床的pid控制，对于抑制数控系统运行过程中的抖振有很好的效果，当数控系统自身参数发生漂移或存在外在干扰时能够实现维持系统鲁棒性，提升加工器件的精度，消除人为失误对产品质量的影响，改善生产条件，提高工业生产效率。

附图说明

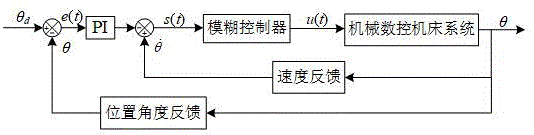
图1为本发明的一种比例积分滑模面的数控机床用模糊滑模位置控制方法的控制策略图；

图2为本发明一种比例积分滑模面的数控机床用模糊滑模位置控制方法的位置与速度跟踪变化曲线。

具体实施方式

为使本发明的目的、技术方案和优点更加清楚明了，下面通过附图及实施例，对本发明进行进一步详细说明。但是应该理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限制本发明的范围。

除非另有定义，本文所使用的所有的技术术语和科学术语与属于本发明的技术领域的技术人员通常理解的含义相同，本文中在本发明的说明书中所使用的术语只是为了描述具体的实施例的目的，不是旨在于限制本发明。

如图1、图2所示，一种比例积分滑模面的数控机床用模糊滑模位置控制方法，包括以下步骤；

步骤一：首先机械数控机床非线性系统进行分析，提取机械数控机床位置的实际反馈值θ，得到与机械数控机床的位置期望值θd的位置误差e(t)；

步骤二：设计比例积分滑模面切换函数，将滑模控制中的切换函数s(t)作为模糊系统的输入；

步骤三：对模糊控制器进行设计，包括根据经验构造模糊规则库，大大减少模糊规则的数量；采用重心算法，将系统进行反模糊化，得到模糊控制器输出u(t)；

步骤四：将机械数控机床位置控制器的位置输出信号u(t)输入数控系统，机械数控机床系统输出的位置角度反馈至输入端。

本实施例，步骤一中的位置误差e(t)计算方法为：

根据系统的输入与输出数据为依据辨识控制系统的结构、参数与模型，以此得到的位置伺服系统模型，模型表达式为：

θ(k)＝f[θ(k-1),θ(k-2),…θ(k-n),θd(k-1),θd(k-2),…θd(k-m)](1)

式中，θ为系统位置角度输出；θd为系统位置角度指令输入；n为系统阶次；m为输出阶次；k为位置环参数；

同时进行时间序列离散化处理，得到式(1)的差分方程表达式：

式中，ai与bj均为辨识的模型参数，其中i为[1，n]中的整数,j为[1，m]为中的整数；

通过上述的模型结构、参数进行辨识，可将网格搜索算法和递推最小二乘法进行结合辨识控制系统的模型结构与参数最终可得到机械数控机床位置伺服系统的数学模型；机械数控机床控制位置角度可表示为：

式中，f和g为机械数控机床中未知的非线性函数；d(t)为机械数控机床运行过程中所受到的干扰，跟踪误差为：

e(t)＝θ(t)-θd(t)(4)

式中，θ为系统位置角度输出；θd为系统位置角度指令输入。

本实施例，步骤二中的比例积分滑模面切换函数为：

式中，k为非零常数，k1和k2为非零正常数；

当滑模控制处于理想状态，则表现为:

通过确定k1和k2，跟踪误差e(t)及其导数趋近于零；相比于机械数控机床传统的pid控制器而言，可以采用切换函数s(t)作为模糊控制器的输入，控制输入u(t)作为模糊系统的输出，构成一个单输入-单输出(siso)模糊系统。

本实施例，步骤三中的模糊控制器设计方法为：

模糊控制器为系统的重要部分，以模糊数学作为理论支柱；首先将机械数控机床切刀的位置控制量的比例积分滑模面切换函数s(t)，作为模糊输入(其中通过对应的模糊语言来具体描述)，此后依照与经验设计的模糊关系对模糊控制器的控制规则进行设计；最后，依据推理得到的控制规则开展模糊决策机制，由此获取模糊控制量u(t)；

该模糊控制器的模糊规则形式为：

rulei:ifsisfsⁱthenuisai(8)

式中，fsⁱ和ai(i＝1,2,,m)分别为输入和输出的模糊集合；

根据专家经验可在在模糊控制系统中建立如下5条模糊规则：

(11)if(sisnb)then(uispb)

(12)if(sisns)then(uisps)

(13)if(sisz)then(uisz)

(14)if(sisps)then(uisns)

(15)if(sispb)then(uisnb)

其中s和u的隶属函数采用“负大”(nb)、“负小(ns)”、“零(z)”、“正小(pb)”、“正大(pb)”。其模糊定义规则为：若s为nb(负大)，则u为ps(正大)；若s为ns(负小)，则u为ps(正小)；若s为z(零)，则u为z(零)；若s为ps(正小)，则u为ns(正小)；若s为pb(负大)，则u为nb(负大)；

最后，依据得到的控制规则开展模糊决策机制；重心法是取隶属度函数曲线与横坐标围成面积的重心作为模糊推理的最终输出值；采用重心法进行反模糊化，得到控制器输出为：

式中，ωi为第i条规则中前提的隶属度，ai为第i条规则中结论的隶属度。

本实施例，步骤四中将机械数控机床位置控制器的位置输出信号u(t)输入数控系统，机械数控机床系统输出的位置角度反馈至输入端，实现位置速度双闭环控制。

本发明仿真结果如图2所示，图2为基于比例积分滑模面的机械数控机床用模糊滑模位置控制中位置与速度值与期望值的变化曲线。从仿真结果可以看出，动态运行过程中，模糊滑模控制的位置角度与速度能够迅速跟踪期望理想值，与实际值的误差很小。同时可以说明，一种比例积分滑模面的数控机床用模糊滑模位置控制方法能够迅速跟踪到达期望位置点，鲁棒性强。

以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换或改进等，均应包含在本发明的保护范围之内。