一种数控机床伺服进给系统控制参数的优选方法

本发明的技术方案属于数控机床伺服进给系统控制技术领域，具体的说是一种数控机床伺服进给系统控制参数的优选方法。

背景技术：

数控技术是指通过对机床进行预先编程来驱动机床对工件进行自动加工的技术。一个国家的机械工业和经济发展水平在很大程度上取决于数控技术及实现该项技术的设备条件。同时，数控技术也是现代制造业的基石。伺服控制技术是数控机床机械控制的关键技术之一，微处理器技术和电力电子技术的发展为伺服控制技术的数字化和智能化奠定了良好基础。数控机床中的伺服进给系统具有高响应、免维护和高可靠性等特点，能够较好地满足目前规模化生产对加工设备高速化、高精度以及高效率的要求。

数字化的伺服控制技术的发展也使得系统参数调整优化更为方便，减小了模拟回路控制的不稳定性。作为数控机床的核心组成部分以及数控机床加工过程的最后一环，数控机床伺服控制技术的主要功能是实现伺服进给系统控制以及主轴伺服系统控制，其性能将直接影响产品的加工精度，所以如何选择合适的数控机床伺服控制模型十分关键。

目前，在数控机床的加工生产过程中，没有具体标准措施对系统中的伺服参数进行调整，这影响了机床的生产效率以及产品的加工质量。在当前已有的数控机床伺服进给系统控制参数的优选方法中，通常对位置环、速度环以及电流环顺序调整，以实现三种伺服参数的准确调整。针对传统pid控制器自整定方法已不能满足伺服系统的要求这一问题，有的学者提出了一种利用单纯形法来自整定伺服系统pid控制器，或将具有较好鲁棒性的模糊控制方法与传统pid控制方法相结合，但是以上几种方式仅对于特定的数控机床伺服控制系统进行参数整定和系统设计，未考虑产品的加工精度。对于复杂情况下系统的参数选择，未能实现参数整定的时效性和准确性，不利于数控机床伺服进给系统的控制参数优选。

因此，根据现有的参数优选方法所得到的伺服进给系统pid控制参数，无法进一步提高数控机床的加工精度以及产品的质量，需要对伺服系统的参数进行重新优选。本发明对现阶段数控机床伺服控制系统进行优化改进来提高数控机床的加工精度。在对数控机床伺服控制系统数学模型分析的基础上，提出了一种改进人群搜索算法来对伺服进给系统中的pid控制参数进行优化，以实现加工精度的改善，提高数控机床的加工水平，同时降低制造成本和延长设备寿命。

技术实现要素：

本发明所要解决的技术问题是：提供一种数控机床伺服进给系统控制参数的优选方法，通过获取需要进行参数优选的数控机床电机，基于电机参数搭建相应的伺服进给系统速度环和位置环数学模型；建立基于改进人群搜索算法的pid控制参数优选模型对伺服进给系统的速度环增益、位置环增益和积分时间常数进行优选；与现有的方法相比，差分进化算法中的变异、杂交和竞争策略使得种群个体多样性增强，并提高算法求解的效率以及跳出局部最优的能力；基于改进人群搜索算法的pid控制参数优选模型能够合理、可靠地对数控机床伺服进给系统的控制参数进行优选，从而进一步提高数控机床的加工精度。

本发明解决该技术问题所采用的技术方案是：一种数控机床伺服进给系统控制参数的优选方法，是基于改进人群搜索算法优化伺服进给系统控制参数的方法，其步骤如下：

步骤一，构建数控机床伺服进给系统中的伺服电机数学模型

本发明采用隐极式同步电机，建立其理想数学模型时，有如下假设条件：忽略饱和现象，将绕组和互感视为线性；忽略涡流和磁滞产生的损耗；忽略环境因素对绕组特性的影响，认为永磁体的磁导率与周围环境相同；三相绕组保持对称，空载电势为正弦波，忽略高次谐波；阻尼绕组可等效为d轴、q轴两个方向上的独立绕组；

(1.1)同步电机三相定子绕组电压方程为：

式(1)中，ua、ub、uc为三相定子绕组电压；ra、rb、rc为三相定子绕组电阻，且三者相等；ia、ib、ic为三相定子绕组电流；为三相定子绕组磁链。进而三相定子绕组磁链方程为：

式(2)中，laa、lbb、lcc为三相定子绕组自感系数；lab、lba、lac和lca、lbc、lcb为绕组互感系数且为相同常数；为转子永磁体的磁链等效到三相定子绕组一侧的磁链；由于三相定子绕组存在对称关系，所以在三相定子绕组一侧，转子永磁体等效磁链方程为：

式(3)中，为转子磁场等效磁链；θ为转子轴线与定子绕组轴线间电气角；由于三相绕组保持对称且在空间上相差120度，因此隐极式同步电机的数学模型的矩阵表达式为：

(1.2)根据矢量变换原理，当永磁同步电机定子的参量转化到d-q旋转坐标系时，伺服进给系统的状态方程为：

式(6)中，id，iq分别是d轴和q轴电流，且计算结果为矢量；v是转子线速度，r是定子绕组电阻值；l是d轴和q轴电感；τ是极距；m为总转动惯量；b为总粘性系数；fl为负载力；为了让参数解耦并获得最大的电磁推力，采用d轴电流为零的控制方式，此时完全解耦后的状态方程为：

永磁同步电机结构模型如图2所示，其中为电机转矩系数；为电机反电势常数；pn为电机磁极对数；l和r为电机绕组线圈电感值和电阻值；j和b为总转动惯量和粘性阻尼系数；

步骤二，构建数控机床伺服进给系统中的控制模型

本发明是对西门子数控系统的伺服进给控制模型进行研究和分析，西门子数控系统的伺服进给控制方式为闭环控制，主要分为电流控制、速度控制和位置控制，其控制流程如图3所示，输入信号通过位置控制到速度控制，再返回到电流控制，最终到伺服电机和编译器；随后，编码器将信号传给位置控制，伺服电机将信号返回至电流控制和速度控制；

(2.1)电流环控制由pwm逆变器、pi控制器、前向滤波器等部分组成，其工作原理如图4所示；在电流环控制模型框图中，pi控制包括电流环比例增益ki和积分时间ti，tif为电流环的反向滤波时间常数，ka为电流环的反向滤波系数，pwm逆变器含有比例增益kpwm以及积分时间tpwm，m代表整个电机和工作台的质量；

由于电流环反向滤波时间常数tif数值极小，故将反向滤波等效为单位反馈系统，且整个电机和工作台的质量m数值远大于积分分子，故可忽略该部分作用，计算得到电流环被控对象的传递函数为：

(2.2)速度环控制原理如图5所示，在速度环控制工作原理框图中，速度环控制主要由pi控制器、前向滤波器和反向滤波构成，其中，kv和tv为速度环比例增益和积分时间，tvf为速度环控制的反向滤波时间常数，kvf为速度环控制的反向滤波系数，进一步通过计算得到速度环的被控对象传递函数模型为：

(2.3)位置环控制可视为一个含反馈系数的反馈系统，电流环控制存在于速度环控制之中，其工作原理框图如图6所示，在位置环控制的工作原理框图中，pid控制器中含有比例增益kp，kpf为位置环反馈系数，进一步通过计算得到伺服进给系统的传递函数模型为：

步骤三，选择需要进行参数优选的数控机床设备

针对数控机床伺服进给系统的伺服电机模型和控制模型，本发明选用某卧式加工中心设备作为伺服控制参数优选的平台，其型号为huellerhillenbh290，在卧式加工中心设备中，其同步电机为西门子公司生产的伺服进给系统专用电机，型号是1ft6108-8ac71-4ag1；

转动惯量包括电机转轴的转动惯量、丝杠的转动惯量以及丝杠与电机中齿轮传动器件的转动惯量；粘性系数包括电机转轴的粘性系数、丝杠的粘性系数以及丝杠与电机中齿轮传动器件的粘性系数；基于电机参数，可以计算得到电机的转矩系数为1.0500，反电势常数为0.7000；伺服进给系统的伺服电机模型和控制模型的参数如表1所示；

表1数控机床伺服进给系统的基本参数

步骤四、对改进人群搜索算法所优化的数学模型进行求解

在huellerhillenbh290卧式加工中心的伺服控制系统中，电流环控制只与伺服电机和驱动相匹配，在不更换伺服电机情况下一般不需要修改电流环控制的参数；速度环控制的稳定对于整个伺服系统的稳定尤为重要，参数匹配的优劣直接影响产品的加工精度，在伺服控制系统中需要对速度增益和积分时间进行调节；位置环控制是伺服控制的最外环，与伺服电机以及负载联系密切，主要进行比例调节；

因此，本发明对数控机床伺服进给系统中的速度环和位置环控制进行参数优选；基于电机参数以及式(9)和式(10)，计算得到相应的速度环和位置环数学模型；

步骤五、参数优选前对数控机床的精度进行检测

在参数优选前，利用雷尼绍cq20球杆仪在xy平面内对x、y轴进行检测，并选取了两轴加工段行程的测试报告；

步骤六，对改进人群搜索算法的参数进行初始化

(6.1)伺服进给系统的优选参数包括速度环增益、位置环增益和积分时间常数，设置改进人群搜索算法的优化维度dim为3；

(6.2)速度环增益、位置环增益和积分时间常数的设置范围如表3所示；

表3x轴的伺服驱动参数取值范围

(6.3)设置改进人群搜索算法的种群规模n为30；

(6.4)设置改进人群搜索算法的最大迭代次数t为100；

(6.5)设置改进人群搜索算法的最大隶属度umax为0.95；设置改进人群搜索算法的最小隶属度umin为0.01；设置改进人群搜索算法的交叉概率cr为0.9；设置改进人群搜索算法的变异概率mu为0.5；

(6.6)设置速度环控制和位置环控制的适应度函数为式(11)和式(12)，以速度环及位置环中的输入量与输出量之间差值的绝对值在整个算法优选过程中的最小累积为目标，并建立适应度函数；此外，为防止速度环及位置环出现输出量u(t)过大的现象，需要添加输出量的平方项来作为限制因素；

式(11)和式(12)中，us(t)和up(t)分别为速度环控制和位置环控制的输出量；es(t)和ep(t)分别表示t时刻在速度环控制和位置环控制中各自输入与输出的差值；ωmax、ωmin分别为权值最大值和权值最小值，且均为[0，1]区间内的常数；

步骤七、使用改进人群搜索算法寻找pid控制的最优参数

(7.1)生成初始化种群，将每一个种群个体对应为伺服进给系统的参数集合，完成搜索位置的确定；

(7.2)将种群个体包含的pid控制参数输入到选定的速度环和位置环控制数学模型中，数控机床根据每次输入的参数信息完成相应的运行动作；根据适应度函数得到相应的适应度值；

(7.3)将种群个体分别进行变异、杂交和竞争操作，完善个体的丰富程度；

采用差分策略来实现种群个体的变异，而常见的差分策略是在种群中随机选取三个不同的个体，并选择其中一个个体作为待变异个体，且另外两个个体在进行向量差缩放操作后与待变异个体进行向量合成，如式(13)所示；

vi(g+1)＝xr1(g)+f·[xr2(g)-xr3(g)](13)

式(13)中，f为缩放因子，其值在[0，2]区间内；i为当前种群个体；r1、r2和r3为最大种群规模内的三个随机数；g为当前迭代的次数；

目标个体和变异个体在进行交叉操作后可得到交叉个体，如式(14)所示；

式(14)中，j为当前迭代次数；cr为交叉概率，取值越大收敛越快，但超过一定阈值后收敛速度下降，所以通常在[0.8，1]区间内取值；

当产生第g+1代个体时，de算法采用贪婪原则，即当前目标个体和交叉个体二者竞争时，下一代的种群个体为适应度值较优的一方，如式(15)所示；

(7.4)计算得到新种群个体在每一维上的搜索步长和搜索方向；

为了确立最优解和步长之间的联系，采用模糊系统的逼近能力并结合高斯隶属函数来确定搜索个体的搜索步长感知变量：

式(16)中，x为输入变量；ua为高斯隶属度；u、δ为隶属度参数，且如果输出变量在区间[u-3δ，u+3δ]外且隶属度小于0.0111时，可使得umin＝0.0111；

采用线性隶属函数使得隶属度与函数值的排列顺序构成正比关系，且最佳位置对应的最大隶属度值为umax＝1.0，最劣位置对应的最小隶属度值为umin＝0.0111，其他位置隶属度值取u＜1.0；为了实现模拟人类的随机搜索，采用rand函数：

uij＝rand(ui，1)(17)

式(17)中，uij为j维搜索空间最优解i的隶属度，j＝1，2，...d，且d是搜索空间维数；ui为最优解i的隶属度；rand(ui，1)表示区间[ui，1]内均匀分布的随机数，进而可以得到步长公式：

式(18)中，αij为j维搜索空间的搜索步长；δij为高斯隶属函数参数，可由式(19)和式(20)得到：

ω＝(gmax-g)/gmax(20)

式(19)和式(20)中，g和gmax分别为当前的迭代次数和最大迭代次数；ω是惯性权值，在寻优过程中动态变化；和分别为种群中最小和最大函数值的位置；

种群个体的搜索方向采用随机加权几何平均的方式在预动行为方向利他行为方向以及利己行为方向上分别确定，然后得到最终的搜索方向，如式(21)到式(24)所示；

式(21)到式(24)中，sign为符号函数；和分别为第i个种群个体所在邻域的集体历史最优位置以及目前搜索到的最优位置；和分别为种群个体在各自t1和t2时刻中内的最佳位置；和为[0，1]区间内的常数，通常取0.5；

种群个体的搜索位置在得到搜索步长和搜索方向后的更新公式如下：

δxij(t+1)＝αijdij(t)(25)

xij(t+1)＝xij(t)+δxij(t+1)(26)

式(25)和式(26)中，xij(t+1)为更新后的搜索位置；δxij(t+1)为搜索位置更新的变化量；

(7.5)将当前pid控制的输入参数以及数控机床的运行动作信息，代入到适应度函数式(11)和(12)进行该次伺服进给系统控制的综合性能评价，得到新的适应度值；

步骤八，对伺服进给系统控制的初始适应度值和当前适应度值进行对比，保留最优适应度，根据评价结果得到pid控制参数中的最优样本值；判断当前的适应度值是否满足迭代结束的原则，若没有达到则继续循环进行，保留当前的适应度值，进入下一次迭代；达到最大循环次数，保存并记录pid控制参数的最终优选结果；

步骤九，输出pid控制参数的优选结果；

步骤九获得的pid控制的优选参数与传统人群搜索算法获得的优选参数进行比较，其对比结果借助matlab软件在计算机的显示屏上显示。在完成参数优选后，在相同区域内再次对该设备xy轴平面进行雷尼绍qc20球杆仪检测。在整个伺服驱动系统中，由于传动摩擦力、负载惯量匹配以及运动系统刚性等多种因素影响进给轴的运动特性。此外，调试过程中的频率特征曲线受惯量、摩擦、弹性和共振等多种影响，使参数优选模型无法对很多控制量精确量化，导致理论算法得出的最优参数与实际值之间有一定偏差，需要根据实际情况进行参数微调。

上述的一种数控机床伺服进给系统控制参数的优选方法，所述的数控机床设备参数，如数控机床伺服进给系统的伺服电机模型和控制模型，加工设备的型号，同步电机的型号以及电机的转动惯量和粘性系数等是为本领域技术人员所熟知的。

上述的一种数控机床伺服进给系统控制参数的优选方法，所述的人群搜索算法、差分进化算法以及pid控制技术是已有技术，是为本技术领域技术人员所熟知的。

上述的一种数控机床伺服进给系统控制参数的优选方法，所述将所获取的数控机床伺服进给系统的速度环和位置环模型以及pid控制的参数优选结果输入计算机中的输入方法是公知的方法；

上述的一种数控机床伺服进给系统控制参数的优选方法，所述雷尼绍qc20球杆仪、计算机、显示器和matlab计算机软件均是通过商购获得的。

本发明的有益结果是：本发明与现有技术相比有以下优点，

(1)本发明在充分考虑了数控机床伺服进给系统的控制环境和周围工作环境对伺服控制优化的影响，以伺服进给系统速度环和位置环的数学模型为基本载体，以改进人群搜索算法为优选方法，以速度环及位置环中的输入量与输出量之间差值的绝对值在整个算法优选过程中的最小累积为目标函数，提出了一种基于改进人群搜索算法的pid控制参数优选模型；

(2)本发明提出的改进人群搜索算法，以差分进化算法中的变异、杂交和竞争策略为改进策略，对其最优解进行全局搜索，提高算法求解的效率以及跳出局部最优的能力；

(3)本发明提出的一种数控机床伺服进给系统控制参数的优选方法，其扩展能力强，影响因素不断扩展，有较强的兼容性，不仅可以用于数控机床伺服进给系统的控制参数优选，也可以扩展到其他领域，如永磁式同步电机驱动系统的pid参数优化，甚至是其他领域应用。

附图说明

下面结合附图和实施例对本发明进一步说明。

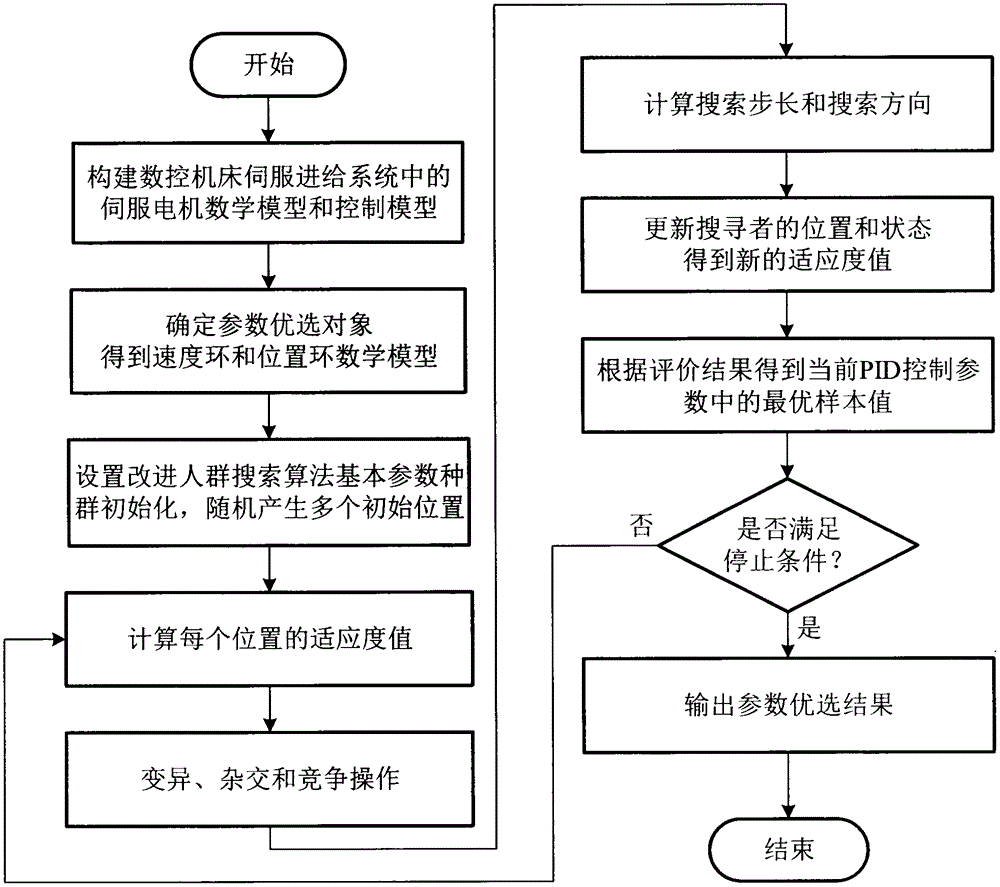
图1是本发明方法的流程示意图。

图2是本发明使用的永磁同步电机结构的数学模型框图。

图3是本发明使用的西门子数控系统控制的示意图。

图4是本发明使用的电流环控制的工作原理框图。

图5是本发明使用的速度环控制的工作原理框图。

图6是本发明使用的位置环控制的工作原理框图。

图7是本发明在参数优选前加工面xy轴平面的检测结果示意图。

图8是本发明优化速度环控制参数得到两种算法的适应度收敛曲线图。

图9是本发明优化位置环控制参数得到两种算法的适应度收敛曲线图。

具体实施方式

本专利旨在对现阶段数控机床伺服控制系统进行优化改进来提高数控机床的加工精度。在对数控机床伺服控制系统数学模型分析的基础上，提出了一种改进人群搜索算法来对伺服进给系统中的pid控制参数进行优化，提高数控机床的加工水平，实现加工精度的改善，同时降低制造成本和延长设备寿命。

人群搜索算法(seekeroptimizationalgorithm，soa)是一种基于模拟人类的智能搜索行为而提出的一种新型启发式随机搜索算法。在人群搜索算法中，需要产生相应的搜索种群，并依次判断种群中每一个体的搜索位置是否为群体的最优解。此外，soa算法在基本群智能算法的原理之上，结合多代理系统中的利己行为、利他行为、不确定性推理行为、预动行为以及自组织聚类行为等，在种群搜索最优解的过程中引入搜索方向和步长，使得种群的位置更新和寻优效果更加迅速。

由于soa算法本身存在局限性，在对模型进行求解时，算法会陷入局部最优值，因此需要对soa算法进行改进来提高算法的求解能力。本文将差分进化算法(differentialevolution，de)与soa算法相结合，提出一种改进人群搜索算法(de-soa)。在soa种群寻优的过程中引入de算法中的变异、杂交和竞争策略，使得种群个体多样性增强，从而提高算法求解的效率以及跳出局部最优的能力。

该数控机床伺服进给系统的参数优流程图如图1所示，其参数优选流程是，开始→构建数控机床伺服进给系统中的伺服电机数学模型和控制模型→选择需要进行参数优选的电机→根据电机参数计算得到相应的速度环和位置环数学模型→对伺服进给系统的参数优选模型进行初始化操作→设置de-soa算法的参数，生成初始化种群，将每一个种群个体对应为伺服进给系统的参数集合，完成搜索位置的确定→将初始化种群中包含的pid控制参数输入到选定的电机数学模型中，并根据适应度函数得到相应的适应度值→种群个体进行变异、杂交和竞争操作→计算新种群个体在每一维上的搜索步长和搜索方向→进行相应的位置更新和状态更新，并计算得到新的适应度值→完成伺服进给系统控制的适应度对比，保留最优适应度→根据评价结果得到当前pid控制参数中的最优样本值→判断当前的适应度值是否满足迭代结束的原则→若没有达到则继续循环进行，保留当前的适应度值，进入下一次迭代→达到最大循环次数，得到pid控制参数的最终优选结果→结束。

实施例

本发明采用pc机作为平台进行模型搭建，其中cpu为i5-5200u2.20ghz，安装内存为4gb，操作系统为windows10-64位，并使用matlabr2016a版本。基于上述设计流程和系统环境，本发明提出一种数控机床伺服进给系统控制参数的优选方法，包括以下步骤：

步骤一，构建数控机床伺服进给系统中的伺服电机数学模型

本发明采用隐极式同步电机，建立其理想数学模型时，有如下假设条件：忽略饱和现象，将绕组和互感视为线性；忽略涡流和磁滞产生的损耗；忽略环境因素对绕组特性的影响，认为永磁体的磁导率与周围环境相同；三相绕组保持对称，空载电势为正弦波，忽略高次谐波；阻尼绕组可等效为d轴、q轴两个方向上的独立绕组；

(1.1)同步电机三相定子绕组电压方程见式(1)，三相定子绕组磁链方程见式(2)；由于三相定子绕组存在对称关系，所以在三相定子绕组一侧，转子永磁体等效磁链方程见式(3)；由于三相绕组保持对称且在空间上相差120度，因此隐极式同步电机的数学模型的矩阵表达式见式(4)和式(5)：

(1.2)根据矢量变换原理，当永磁同步电机定子的参量转化到d-q旋转坐标系时，伺服进给系统的状态方程见式(6)；为了让参数解耦并获得最大的电磁推力，采用d轴电流为零的控制方式，此时完全解耦后的状态方程见式(7)；永磁同步电机结构模型如图2所示，其中为电机转矩系数；为电机反电势常数；pn为电机磁极对数；l和r为电机绕组线圈电感值和电阻值；j和b为总转动惯量和粘性阻尼系数；

步骤二，构建数控机床伺服进给系统中的控制模型

本发明是对西门子数控系统的伺服进给控制模型进行研究和分析，西门子数控系统的伺服进给控制方式为闭环控制，主要分为电流控制、速度控制和位置控制，其控制流程如图3所示，输入信号通过位置控制到速度控制，再返回到电流控制，最终到伺服电机和编译器；随后，编码器将信号传给位置控制，伺服电机将信号返回至电流控制和速度控制；

(2.1)电流环控制由pwm逆变器、pi控制器、前向滤波器等部分组成，其工作原理如图4所示；在电流环控制模型框图中，pi控制包括电流环比例增益ki和积分时间ti，tif为电流环的反向滤波时间常数，ka为电流环的反向滤波系数，pwm逆变器含有比例增益kpwm以及积分时间tpwm，m代表整个电机和工作台的质量；

由于电流环反向滤波时间常数tif数值极小，故将反向滤波等效为单位反馈系统，且整个电机和工作台的质量m数值远大于积分分子，故可忽略该部分作用，计算得到电流环被控对象的传递函数见式(8)；

(2.2)速度环控制原理如图5所示，在速度环控制工作原理框图中，速度环控制主要由pi控制器、前向滤波器和反向滤波构成，其中，kv和tv为速度环比例增益和积分时间，tvf为速度环控制的反向滤波时间常数，kvf为速度环控制的反向滤波系数，进一步通过计算得到速度环的被控对象传递函数模型见式(9)；

(2.3)位置环控制可视为一个含反馈系数的反馈系统，电流环控制存在于速度环控制之中，其工作原理框图如图6所示，在位置环控制的工作原理框图中，pid控制器中含有比例增益kp，kpf为位置环反馈系数，进一步通过计算得到伺服进给系统的传递函数模型见式(10)；

步骤三，选择需要进行参数优选的数控机床设备

针对数控机床伺服进给系统的伺服电机模型和控制模型，本发明选用某卧式加工中心设备作为伺服控制参数优选的平台，其型号为huellerhillenbh290，在卧式加工中心设备中，其同步电机为西门子公司生产的伺服进给系统专用电机，型号是1ft6108-8ac71-4ag1；

转动惯量包括电机转轴的转动惯量、丝杠的转动惯量以及丝杠与电机中齿轮传动器件的转动惯量；粘性系数包括电机转轴的粘性系数、丝杠的粘性系数以及丝杠与电机中齿轮传动器件的粘性系数；基于电机参数，可以计算得到电机的转矩系数为1.0500，反电势常数为0.7000；伺服进给系统的伺服电机模型和控制模型的参数如表1所示；

步骤四、对改进人群搜索算法所优化的数学模型进行求解

在huellerhillenbh290卧式加工中心的伺服控制系统中，电流环控制只与伺服电机和驱动相匹配，在不更换伺服电机情况下一般不需要修改电流环控制的参数；速度环控制的稳定对于整个伺服系统的稳定尤为重要，参数匹配的优劣直接影响产品的加工精度，在伺服控制系统中需要对速度增益和积分时间进行调节；位置环控制是伺服控制的最外环，与伺服电机以及负载联系密切，主要进行比例调节；

因此，本发明对数控机床伺服进给系统中的速度环和位置环控制进行参数优选；基于电机参数以及式(9)和式(10)，计算得到相应的速度环和位置环数学模型；

步骤五、参数优选前对数控机床的精度进行检测

在参数优选前，利用雷尼绍cq20球杆仪在xy平面内对x、y轴进行检测，并选取了两轴加工段行程的测试报告，如图7和表2所示。

表2优选加工前检测结果

从图7和表2中可以得到，圆度误差为177.5μm，且两轴伺服不匹配的数据诊断值为10.14ms，表明两轴插补联动运行中存在伺服不匹配问题，x轴明显滞后于y轴。此外，曲线中有噪点，说明两个轴中有轻微抖动的问题，可能与机械或者伺服控制有关。由于前期机械问题已经排除，进而尝试通过伺服控制参数优选来进一步改善抖动问题。通过系统工具对两轴做频率响应测试和trace测试发现x轴y轴都存在相应问题，且x轴存在问题较为明显，因此以x轴为例来检测参数优选前后的有效性。

步骤六，对改进人群搜索算法的参数进行初始化

(6.1)伺服进给系统的优选参数包括速度环增益、位置环增益和积分时间常数，设置改进人群搜索算法的优化维度dim为3；

(6.2)速度环增益、位置环增益和积分时间常数的设置范围如表3所示；

(6.3)设置改进人群搜索算法的种群规模n为30；

(6.4)设置改进人群搜索算法的最大迭代次数t为100；

(6.5)设置改进人群搜索算法的最大隶属度umax为0.95；设置改进人群搜索算法的最小隶属度umin为0.01；设置改进人群搜索算法的交叉概率cr为0.9；设置改进人群搜索算法的变异概率mu为0.5；

(6.6)设置速度环控制和位置环控制的适应度函数见式(11)和式(12)，以速度环及位置环中的输入量与输出量之间差值的绝对值在整个算法优选过程中的最小累积为目标，并建立适应度函数；此外，为防止速度环及位置环出现输出量u(t)过大的现象，需要添加输出量的平方项来作为限制因素；

步骤七、使用改进人群搜索算法寻找pid控制的最优参数

(7.1)生成初始化种群，将每一个种群个体对应为伺服进给系统的参数集合，完成搜索位置的确定；

(7.2)将种群个体包含的pid控制参数输入到选定的速度环和位置环控制数学模型中，数控机床根据每次输入的参数信息完成相应的运行动作；根据适应度函数得到相应的适应度值；

(7.3)将种群个体分别进行变异、杂交和竞争操作，完善个体的丰富程度；

采用差分策略来实现种群个体的变异，而常见的差分策略是在种群中随机选取三个不同的个体，并选择其中一个个体作为待变异个体，且另外两个个体在进行向量差缩放操作后与待变异个体进行向量合成，如式(13)所示；

目标个体和变异个体在进行交叉操作后可得到交叉个体，如式(14)所示；

当产生第g+1代个体时，de算法采用贪婪原则，即当前目标个体和交叉个体二者竞争时，下一代的种群个体为适应度值较优的一方，如式(15)所示；

(7.4)计算得到新种群个体在每一维上的搜索步长和搜索方向；

为了确立最优解和步长之间的联系，采用模糊系统的逼近能力并结合高斯隶属函数来确定搜索个体的搜索步长感知变量，如式(16)所示；

采用线性隶属函数使得隶属度与函数值的排列顺序构成正比关系，且最佳位置对应的最大隶属度值为umax＝1.0，最劣位置对应的最小隶属度值为umin＝0.0111，其他位置隶属度值取u＜1.0；为了实现模拟人类的随机搜索，采用rand函数，如式(17)所示；步长公式见式(18)；高斯隶属函数参数由式(19)和式(20)得到；

种群个体的搜索方向采用随机加权几何平均的方式在需要在预动行为方向利他行为方向以及利己行为方向上分别确定，然后得到最终的搜索方向，如式(21)到式(24)所示；种群个体的搜索位置在得到搜索步长和搜索方向后的更新见式(25)和式(26)；

(7.5)将当前pid控制的输入参数以及数控机床的运行动作信息，代入到适应度函数式(11)和(12)进行该次伺服进给系统控制的综合性能评价，得到新的适应度值；

步骤八，对伺服进给系统控制的初始适应度值和当前适应度值进行对比，保留最优适应度，根据评价结果得到pid控制参数中的最优样本值；判断当前的适应度值是否满足迭代结束的原则，若没有达到则继续循环进行，保留当前的适应度值，进入下一次迭代；达到最大循环次数，保存并记录pid控制参数的最终优选结果；

步骤九，输出pid控制参数的优选结果；

步骤九获得的pid控制的优选参数与soa算法获得的优选参数进行比较，其对比结果借助matlab软件在计算机的显示屏上显示，其速度环和位置环控制的仿真过程和参数优选结果如图8、图9以及表4所示；

从图8和图9中可以看到，soa算法和de-soa算法在搜索后期都能够更好地靠近目标值；从表4中可知，在速度环控制中，soa算法的最优个体适应度值为20.7431，de-soa算法的最优个体适应度值为20.6989；在位置环控制中，soa算法的最优个体适应度值为20.7274，de-soa算法的最优个体适应度值为20.6941，可证明de-soa算法的优化效果最具竞争力；因此，提出的参数优选模型可以应用到伺服控制系统之中，从而使得到最优的匹配值成为可能；

表4数控机床伺服进给系统的x轴参数优选结果

在完成参数优选后，在相同区域内再次对该设备xy轴平面进行雷尼绍qc20球杆仪检测，圆度测试结果如表5所示；

表5优化后的圆度检测结果

从表5中可以发现，优化后两轴伺服不匹配的问题得到了明显改善，且两轴联动圆度误差从原来的177.5μm减小到20.5μm，其圆度误差降低了88.42％，圆度误差明显改善，在各种倍率下，手动测试和自动测试均显示双轴的运行状态处于运行平稳状态且负载正常，结果表明该台设备在经过伺服参数优选后，伺服系统得到了明显优化，轮廓精度得到了提高；

由步骤九的参数优选结果可以得出，该平台的速度环增益为28.63，速度环积分时间为17.69，位置环增益为2.57；将参数优选结果输入到伺服控制系统并进行速度环控制和位置环控制的频率响应测试，x轴在一定程度上起到了优化效果，该轴速度环和位置环的频率响应得到了改善；数重新优选后的x轴的频率特性曲线中的带宽明显变宽，拐点频率增高，中高频段也变得相对平滑稳定，说明通过参数优选在一定程度上改善了老旧数控机床的动态特性；

在整个伺服驱动系统中，由于传动摩擦力、负载惯量匹配以及运动系统刚性等多种因素影响进给轴的运动特性。此外，调试过程中的频率特征曲线受惯量、摩擦、弹性和共振等多种影响，使参数优选模型无法对很多控制量精确量化，导致理论算法得出的最优参数与实际值之间有一定偏差，需要根据实际情况进行参数微调。

表6x轴参数优选的对比结果

x轴的最终参数优选结果如表6所示，将最终的工程调试值输入到伺服控制系统，并重新设置滤波器；整个参数优选完成后，重新加工并对工件进行3d检验，结果显示几何精度和光洁度均满足精度要求；通过参数优选明显改善了数控机床的加工精度，也验证了参数优选模型在数控机床伺服进给系统驱的参数优选方面具有一定实用性和可靠性。

上述的实施案例中，所述的数控机床设备参数，如数控机床伺服进给系统的伺服电机模型和控制模型，加工设备的型号，同步电机的型号以及电机的转动惯量和粘性系数等是为本领域技术人员所熟知的；所述的人群搜索算法、差分进化算法以及pid控制技术是已有技术，是为本技术领域技术人员所熟知的；所述将所获取的数控机床伺服进给系统的速度环和位置环模型以及pid控制的参数优选结果输入计算机中的输入方法是公知的方法；所述雷尼绍qc20球杆仪、计算机、显示器和matlab计算机软件均是通过商购获得的。

以上仅为本发明较好的实施方式，但本发明的保护范围并不仅限于此，任何熟悉本技术领域的技术人员在本发明披露的技术范围内，根据本发明的技术方案及其发明构思加以等同替换或改变，都应涵盖在本发明的保护范围。