一种复杂网络的同步控制方法及其在图像加密中的应用

本发明属于非线性动力系统领域，具体涉及一种复杂网络的同步控制方法，一种复杂网络的构建方法，一种复杂网络的同步控制装置，一种复杂网络的同步控制终端，以及一种复杂网络在图像加密中的应用。

背景技术：

复杂网络是一种能够有效描述万维网、流行病传播网络、基因网络、通信网络、神经网络、生物网络等的建模工具。复杂网络通常由许多相互连接的节点组成，每个节点具有复杂的动态行为。同时，由于节点之间的相互作用，复杂网络的动态特性更加复杂。由于复杂网络广泛应用于实际场景，其动态行为引起了研究者的关注。目前对复杂网络动态特性的研究较多，如耗散性、稳定性、一致性等。值得一提的是，分数阶理论是整数阶理论的扩展。分数阶网络不仅比整数阶网络具有更大的存储空间和更大的自由度，而且具有许多独特的动态特性。现实中的许多网络都具有丰富的分数阶动态行为。因此，分数阶理论能够更准确地描述实际网络。

复值网络比实值网络具有更多的变量，增加了系统可以传输的信息内容，保证了传输的安全性。同时，复杂网络的复杂动态特性可以更准确地描述许多实际问题。在自然界中，同步现象无处不在，尤其是科学技术迅速发展的今天，同步控制在通讯系统、激光系统等系统中有着广阔的应用。同步作为复杂网络之间非常重要的动态特性，长期以来一直是研究热点。一般来说，它是指随着时间的推移，所有系统的状态趋向于一种共同行为的过程。目前本领域技术人员研究的同步类型包括：完全同步，反同步，相位同步，滞后同步，投影同步等等。其中，投影同步通过引入投影因子来反映同步状态之间的比例关系，通过调整投影因子可以实现完全同步和反同步。特别是复投影同步复投影同步，最早由wu等人提出。复投影同步比实投影同步条件更严格，更适用于真实网络。因此，对复投影同步的研究具有重要意义。

需要指出的是，许多网络在现实环境中容易受到不确定性的影响，这使得网络中的参数很难确定；另外，许多真实网络中的耦合参数也会随环境的变化而变化，这些都可能会导致同步中断甚至失效。在解决复杂网络的同步性问题时，有必要考虑时变参数对同步的影响，但是目前提出的各种同步控制器中均未能针对该问题进行改进，导致复杂网络的同步性变差。

复杂网络的同步控制在通讯系统、激光系统，电力系统等系统中将具有非常广阔的应用，例如可以采用同步的复杂网络在图像处理中实现图像的加密和解密等。

技术实现要素：

针对现有技术中复杂网络同步性差，复杂网络的复投影同步难以实现，以及无法在图像加密中进行应用的问题，本发明提供了一种复杂网络的同步控制方法及其在图像加密中的应用。

本发明采用以下技术方案实现：

一种复杂网络的同步控制方法，其用于实现n维分数阶时变耦合复杂网络中各节点的状态与目标同步节点状态的同步，该同步控制方法包括如下步骤：

步骤s1：根据n维分数阶时变耦合复杂网络需要达到的目标同步状态，建立表征目标同步状态的方程。

步骤s2：设计同步控制器uk(t)，同步控制器uk(t)的设计方法包括步骤：

步骤s21：定义投影同步误差ek(t)，表征投影同步误差ek(t)的方程为：

ek(t)＝xk(t)-vη(t),k＝1,2,...,n

其中，xk(t)表示n维分数阶时变耦合复杂网络中第k个节点的状态变量；η(t)表示目标同步状态的状态变量；v是投影因子，反映的是n维分数阶时变耦合复杂网络与目标同步状态的比例关系，ek(t)表示复杂网络中第k个节点与目标同步状态间的误差。

步骤s22：根据投影同步误差ek(t)的方程，设计自适应控制器，将自适应控制器作为实现同步所需的同步控制器uk(t)，同步控制器uk(t)的方程为：

uk(t)＝vf(η(t))-f(xk(t))-dk(t)γek(t)-bek(t),k＝1,2,...,n

其中，dk(t)表示同步控制器uk(t)的反馈增益；γ＝diag(l1,l2,...,ln)＞0表示内部耦合连接矩阵；，函数f(·)与n维分数阶时变耦合复杂网络的模型中对应的函数符号表示的函数相同；b表示一个可调节的正常数，且满足ai≤b,i＝1,2,..,n，ai为n维分数阶时变耦合复杂网络的模型中一个有界的不确定参数矩阵a＝diag(a1,a2,...,an)中的元素。

步骤s23：设计n维分数阶时变耦合复杂网络中的自适应耦合强度c(t)，自适应耦合器c(t)的自适应律的表达式如下：

其中，表示对t求α次分数阶导数的标记；ε表示一个可调的正常数，γ＝diag(l1,l2,...,ln)＞0表示内部耦合连接矩阵，,表示投影同步误差ek(t)的共轭转置；gkj表示耦合配置矩阵g＝(gkj)∈r^n×n中的元素；其满足

步骤s3：利用设计的自适应耦合强度c(t)对n维分数阶时变耦合复杂网络的模型进行调整，并将同步控制器uk(t)引入到n维分数阶时变耦合复杂网络各节点中。所得受控网络如下：

其中，0<α<1表示分数阶；xk(t)＝(xk1(t),xk2(t),...,xkn(t))^t∈cⁿ是第k个节点的状态变量；f(xk(t))∈cⁿ表示与xk(t)的非线性向量函数；γ＝diag(l1,l2,...,ln)＞0表示内部耦合连接矩阵,c(t)表示时变耦合强度，其值随着系统状态的变化而变化；a＝diag(a1,a2,...,an)表示参数矩阵,gkj表示一个耦合配置矩阵g＝(gkj)∈r^n×n中的元素；

进一步的，耦合配置矩阵g＝(gkj)∈r^n×n中的元素gkj满足如下关系：

进一步地，步骤s1中，表征目标同步状态的方程为：

进一步的，步骤s22中，同步控制器uk(t)中反馈增益dk(t)的表达式如下：

其中，p表示一个可调的参数，且为正常数。

本发明还包括复杂网络的构建方法，利用该方法构建的n维分数阶时变耦合复杂网络可实现各节点与目标同步状态中的节点达到同步，构建方法如下：

步骤s1：构建n维分数阶时变耦合复杂网络的模型，模型为：

其中，0<α<1表示分数阶，xk(t)＝(xk1(t),xk2(t),...,xkn(t))^t∈cⁿ是第k个节点的状态变量；γ＝diag(l1,l2,...,ln)＞0表示内部耦合连接矩阵,f(xk(t))∈cⁿ表示与状态向量xk(t)相关的非线性向量函数；c(t)表示时变耦合强度，其值随着系统状态的变化而变化；

a＝diag(a1,a2,...,an)表示参数矩阵，gkj表示一个耦合配置矩阵g＝(gkj)∈r^n×n中的元素。

耦合配置矩阵g＝(gkj)∈r^n×n中的元素gkj满足如下关系：

步骤s2：根据n维分数阶时变耦合复杂网络需要达到的目标同步状态，建立表征目标同步状态的方程。

步骤s3：设计同步控制器uk(t)，同步控制器uk(t)的设计方法包括步骤：

步骤s31：定义投影同步误差ek(t)，表征投影同步误差ek(t)的方程为：

ek(t)＝xk(t)-vη(t),k＝1,2,...,n

其中，xk(t)表示n维分数阶时变耦合复杂网络中第k个节点的状态变量；η(t)表示需要达到的目标同步状态中的状态变量；v是投影因子，反映的是n维分数阶时变耦合复杂网络与同步状态的比例关系；投影同步误差ek(t)反映了复杂网络中第k个节点与目标同步状态间的误差。

步骤s32：根据投影同步误差ek(t)的方程，设计自适应控制器，将自适应控制器作为实现同步所需的同步控制器uk(t)，同步控制器uk(t)的方程为：

uk(t)＝vf(η(t))-f(xk(t))-dk(t)γek(t)-bek(t),k＝1,2,...,n

其中，dk(t)表示同步控制器uk(t)的反馈增益；γ＝diag(l1,l2,...,ln)＞0表示内部耦合连接矩阵；f(η(t))表示关于同步状态中状态变量的一个非线性向量函数，函数f(·)与n维分数阶时变耦合复杂网络的模型中对应的函数符号表示的函数相同；b表示一个可调节的正常数，且满足ai≤b,i＝1,2,..,n，ai为n维分数阶时变耦合复杂网络的模型中一个有界的不确定参数矩阵a＝diag(a1,a2,...,an)中的元素。

步骤s33：设计n维分数阶时变耦合复杂网络中自适应耦合强度c(t)的自适应律的

表达式如下：

其中，表示对t求α次分数阶导数的标记；ε表示一个可调的正常数，表示投影同步误差ek(t)的共轭转置，gkj表示耦合配置矩阵g＝(gkj)∈r^n×n中的元素，其满足

步骤s4：利用设计的自适应耦合强度c(t)对n维分数阶时变耦合复杂网络的模型进行调整，并将同步控制器uk(t)引入到n维分数阶时变耦合复杂网络各节点中。

进一步的，步骤s2中，表征目标同步状态的方程为：

进一步的，步骤s32中，同步控制器uk(t)中反馈增益dk(t)的表达式如下：

其中，p表示一个可调的参数，且为正常数。

本发明还包括一种复杂网络的同步控制装置，该同步控制装置采用如前述复杂网络的同步控制方法，实现n维分数阶时变耦合复杂网络中各节点与目标同步状态的节点达到同步，同步控制装置包括：同步控制器、自适应耦合强度模块以及修正模块。

其中，同步控制器为一种自适应控制器，该自适应控制器作为实现同步所需的同步控制器uk(t)。

同步控制器uk(t)的方程为：

uk(t)＝vf(η(t))-f(xk(t))-dk(t)γek(t)-bek(t),k＝1,2,...,n

其中，dk(t)表示同步控制器uk(t)的反馈增益；γ表示内部耦合连接矩阵，γ＝diag(l1,l2,...,ln)＞0；函数f(·)与n维分数阶时变耦合复杂网络的模型中对应的函数符号表示的函数相同；b表示一个可调节的正常数，且满足ai≤b,i＝1,2,..,n，ai为n维分数阶时变耦合复杂网络的模型中一个有界的不确定参数矩阵a＝diag(a1,a2,...,an)中的元素；

自适应耦合强度模块用于调节n维分数阶时变耦合复杂网络中时变耦合强度c(t)。

自适应耦合强度c(t)的自适应律的表达式如下：

其中，表示对t求α次分数阶导数的标记；ε表示一个可调的正常数，表示投影同步误差ek(t)的共轭转置，γ＝diag(l1,l2,...,ln)＞0表示内部耦合连接矩阵，,gkj表示耦合配置矩阵g＝(gkj)∈r^n×n中的元素；其满足

修正模块用于将设计的同步控制器和自适应耦合强度模块引入到n维分数阶时变耦合复杂网络的模型中，实现n维分数阶时变耦合复杂网络中的节点与目标同步状态的节点达到同步。

本发明还包括一种复杂网络的同步控制终端，该终端包括存储器、处理器以及存储在存储器上并可在处理器上运行的计算机程序，处理器执行程序时实现如前述的复杂网络的同步控制方法的步骤。

本发明还包括一种复杂网络在图像加密中的应用，采用如前述的复杂网络的同步控制方法可以实现复杂网络中各节点与目标同步状态达到同步，复杂网络为n维分数阶时变耦合复杂网络；应用目标同步状态及与其达到同步的n维分数阶时变耦合复杂网络可以实现对图像进行加密和解密。

其中，图像的加密过程如下：

(1a)利用目标同步状态中节点的状态变量产生混沌信号，提取混沌信号的实部作为加密序列，提取混沌信号的虚部作为置乱序列；

(2a)对原始图像进行序列化处理，得到像素矩阵；

(3a)利用置乱序列对像素矩阵进行置乱操作，得到置乱像素矩阵；

(4a)利用加密序列对置乱像素矩阵进行加密运算，得到加密像素矩阵；

(5a)对加密像素矩阵进行反序列化处理得到加密图像。

加密图像的解密过程如下：

(1b)由同步后的n维分数阶时变耦合复杂网络产生同步混沌信号，提取同步混沌信号的实部作为解密序列，提取同步混沌信号的虚部作为反置乱序列；

(2b)对获取的加密图像进行序列化处理得到加密像素矩阵；

(3b)利用解密序列对加密像素矩阵进行解密运算得到置乱像素矩阵；

(4b)利用反置乱序列对置乱像素矩阵进行反置乱操作，得到像素矩阵；

(5b)对像素矩阵进行反序列化处理得到原始图像。

其中，加密序列和解密序列为完全同步的相同序列；置乱序列和反置乱序列为完全同步的相同序列；解密运算为加密运算的逆运算；反置乱操操作为置乱操作的逆操作。

本发明提供的技术方案，具有如下有益效果：

本发明提出了一种n维分数阶时变耦合复杂网络的同步控制方法、装置，该方法设计的同步控制器考虑了复杂网络中的不确定性，因此采取了一种无需预先确定复杂网络中参数的自适应控制器作为复杂网络的同步控制器。使用该同步控制器的复杂网络的同步性能较好，复杂网络中的耦合参数随环境的变化而变化时，不会再出现同步中断甚至失效的状况。

本发明提供的能实现与目标同步状态同步的n维分数阶时变耦合复杂网络，在医学、通信、电力等系统中有着广泛的应用前景，例如可以在核磁共振仪、电力网络的同步检测器、对调制信号的相干解调、保密通信、图像加密等方向进行实际应用。

附图说明

附图用来提供对本发明的进一步理解，并且构成说明书的一部分，与本发明的实施例一起用于解释本发明，并不构成对本发明的限制。在附图中：

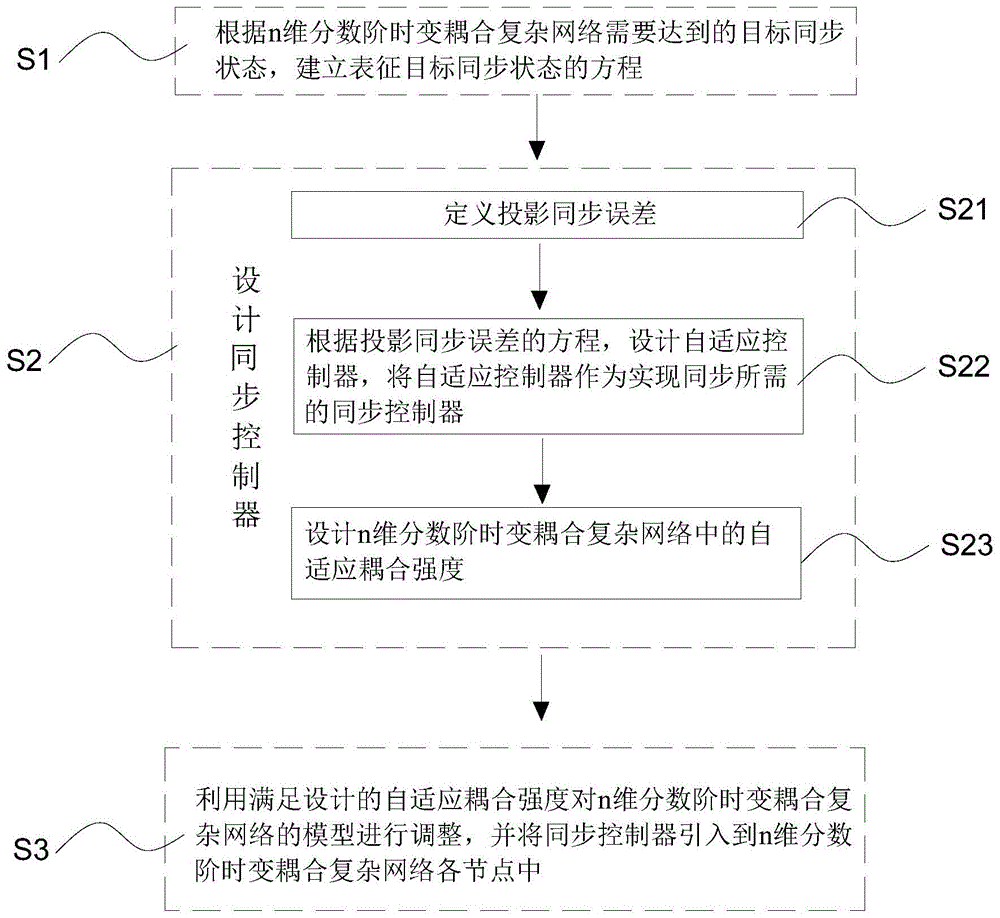
图1为本发明实施例1中一种n维分数阶时变耦合复杂网络的同步控制方法的流程图；

图2为本发明实施例3中，三维分数阶时变耦合复杂网络中节点的第一维度与目标同步状态间的实部误差曲线；

图3为本发明实施例3中，三维分数阶时变耦合复杂网络中节点的第二维度与目标同步状态间的实部误差曲线；

图4为本发明实施例3中，三维分数阶时变耦合复杂网络中节点的第三维度与目标同步状态间的实部误差曲线；

图5为本发明实施例3中，三维分数阶时变耦合复杂网络中节点的第一维度与目标同步状态间的虚部误差曲线；

图6为本发明实施例3中，三维分数阶时变耦合复杂网络中节点的第二维度与目标同步状态间的虚部误差曲线；

图7为本发明实施例3中，三维分数阶时变耦合复杂网络中节点的第三维度与目标同步状态间的虚部误差曲线；

图8为本发明实施例3中同步控制器反馈增益的变化曲线；

图9为本发明实施例3中分数阶时变耦合复杂网络中自适应耦合强度的变化曲线；

图10为本发明实施例4中复杂网络的同步控制装置的模块示意图；

图11为本发明实施例6中应用目标同步状态和达到同步的n维分数阶时变耦合复杂网络实现图像加密和解密的方法流程图(图中左半部分为图像加密过程，右半部分为图像解密过程)。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明。

实施例1

如图1所示，本实施例提供一种n维分数阶时变耦合复杂网络的同步控制方法，该同步控制方法用于实现n维分数阶时变耦合复杂网络中各节点与目标同步状态中的节点达到同步，该同步方法包括如下步骤：

步骤s1：根据n维分数阶时变耦合复杂网络需要达到的目标同步状态，建立表征目标同步状态的方程。

步骤s2：设计同步控制器uk(t)，同步控制器uk(t)的设计方法包括步骤：

步骤s21：定义投影同步误差ek(t)，表征所述投影同步误差ek(t)的方程为：

ek(t)＝xk(t)-vη(t),k＝1,2,...,n

其中，xk(t)表示n维分数阶时变耦合复杂网络中第k个节点的状态变量；η(t)表示目标同步状态的状态变量；v是投影因子，反映的是n维分数阶时变耦合复杂网络与目标同步状态的比例关系，ek(t)表示复杂网络中第k个节点与目标同步状态间的误差。

步骤s22：根据投影同步误差ek(t)的方程，设计自适应控制器，将所述自适应控制器作为实现同步所需的同步控制器uk(t)，同步控制器uk(t)的方程为：

uk(t)＝vf(η(t))-f(xk(t))-dk(t)γek(t)-bek(t),k＝1,2,...,n

其中，dk(t)表示同步控制器uk(t)的反馈增益；γ＝diag(l1,l2,...,ln)＞0表示内部耦合连接矩阵；函数f(·)与n维分数阶时变耦合复杂网络的模型中对应的函数符号表示的函数相同；b表示一个可调节的正常数，且满足ai≤b,i＝1,2,..,n，ai为n维分数阶时变耦合复杂网络的模型中参数矩阵a＝diag(a1,a2,...,an)中的元素。

步骤s23：设计n维分数阶时变耦合复杂网络中的自适应耦合强度c(t)，自适应耦合器c(t)的自适应律的表达式如下：

其中，表示对t求α次分数阶导数的标记；ε表示一个可调的正常数，表示投影同步误差ek(t)的共轭转置；γ＝diag(l1,l2,...,ln)＞0表示内部耦合连接矩阵,gkj表示耦合配置矩阵g＝(gkj)∈r^n×n中的元素，其满足

步骤s3：利用设计的自适应耦合强度c(t)对n维分数阶时变耦合复杂网络的模型中的时变耦合强度进行调整，并将同步控制器uk(t)引入到n维分数阶时变耦合复杂网络各节点中。

该同步方法应用的n维分数阶时变耦合复杂网络的模型为：

其中，0<α<1表示分数阶；xk(t)＝(xk1(t),xk2(t),...,xkn(t))^t∈cⁿ表示第k个节点的状态变量；γ＝diag(l1,l2,...,ln)＞0表示内部耦合连接矩阵,f(xk(t))∈cⁿ表示与状态向量xk(t)有关的非线性向量函数；c(t)表示时变耦合强度，其值随着系统状态的变化而变化；a＝diag(a1,a2,...,an)表示参数矩阵，gkj表示耦合配置矩阵g＝(gkj)∈r^n×n中的元素。

其中，耦合配置矩阵g＝(gkj)∈r^n×n中的元素gkj满足如下关系：

本实施例的步骤s1中，表征目标同步状态的方程为：

本实施例的步骤s22中，同步控制器uk(t)中反馈增益dk(t)的表达式如下：

其中，p表示一个可调的参数，且为正常数。

实施例2

在实施例的1的方法的基础上，本实施例进一步提供一种n维分数阶时变耦合复杂网络的构建方法，构建的该n维分数阶时变耦合复杂网络可实现各节点状态与目标同步节点状态中的同步，构建方法如下：

步骤s1：构建由n个节点n维分数阶时变耦合复杂网络的模型，模型为：

其中，0<α<1表示分数阶；xk(t)＝(xk1(t),xk2(t),...,xkn(t))^t∈cⁿ是第k个节点的状态变量；

γ＝diag(l1,l2,...,ln)＞0表示内部耦合连接矩阵,f(xk(t))∈cⁿ表示与xk(t)相关的非线性向量函数；c(t)表示时变耦合强度，其值随着系统状态的变化而变化；a＝diag(a1,a2,...,an)表示一个参数矩阵，gkj表示一个耦合配置矩阵g＝(gkj)∈r^n×n中的元素。

所述耦合配置矩阵g＝(gkj)∈r^n×n中的元素gkj满足如下关系：

步骤s2：根据n维分数阶时变耦合复杂网络需要达到的目标同步状态，建立表征目标同步状态的方程；表征目标同步状态的方程为：

其中，表示对t求α次分数阶导数的标记；η(t)表示需要达到的同步状态中的状态变量；函数f(·)与n维分数阶时变耦合复杂网络的模型中对应的函数符号表示的函数相同。

步骤s3：设计同步控制器uk(t)，所述同步控制器uk(t)的设计方法包括步骤：

步骤s31：定义投影同步误差ek(t)，表征所述投影同步误差ek(t)的方程为：

ek(t)＝xk(t)-vη(t),k＝1,2,...,n

其中，xk(t)表示n维分数阶时变耦合复杂网络中第k个节点的状态变量；η(t)表示需要达到的目标同步状态中的状态变量；v是投影因子，反映的是n维分数阶时变耦合复杂网络中各节点状态与目标同步状态间的比例关系；投影同步误差ek(t)反映了复杂网络中第k个节点与目标同步状态间的误差。

步骤s32：根据投影同步误差ek(t)的方程，设计自适应控制器，将自适应控制器作为实现同步所需的同步控制器uk(t)，同步控制器uk(t)的方程为：

uk(t)＝vf(η(t))-f(xk(t))-dk(t)γek(t)-bek(t),k＝1,2,...,n

其中，dk(t)表示所述同步控制器uk(t)的反馈增益；γ＝diag(l1,l2,...,ln)＞0表示内部耦合连接矩阵；f(η(t))表示关于同步状态中状态变量的一个非线性向量函数，所述函数f(·)与n维分数阶时变耦合复杂网络的模型中对应的函数符号表示的函数相同；b表示一个可调节的正常数，且满足ai≤b,i＝1,2,..,n，ai为n维分数阶时变耦合复杂网络的模型中一参数矩阵a＝diag(a1,a2,...,an)中的元素。

同步控制器uk(t)中反馈增益dk(t)的表达式如下：

其中，p表示一个可调的参数，且为正常数。

步骤s33：设计n维分数阶时变耦合复杂网络中自适应耦合强度c(t)的自适应律的表达式如下：

其中，表示对t求α次分数阶导数的标记；ε表示一个可调的正常数，γ＝diag(l1,l2,...,ln)＞0表示内部耦合连接矩阵,表示投影同步误差ek(t)的共轭转置；

gkj表示耦合配置矩阵g＝(gkj)∈r^n×n中的元素，其满足

步骤s4：利用设计的自适应耦合强度c(t)对n维分数阶时变耦合复杂网络的模型中时变耦合强度进行调整，并将同步控制器uk(t)引入到n维分数阶时变耦合复杂网络各节点中。

实施例3

本实施例中主要包括两项内容：

其一是对实施例1的提供的n维分数阶时变耦合复杂网络的同步方法的有效性进行理论证明。

其二是通过数值仿真的方法对实施例2中构建的n维分数阶时变耦合复杂网络中各节点状态与目标同步节点状态之间可以达到同步进行验证。

(理论证明和仿真实验均不用于限定本发明，在其它实施例中可以不进行仿真实验，也可以采用其他实验方案进行试验。)

一、理论证明

证明过程如下：

根据本实施例中n维分数阶时变耦合复杂网络的模型，构造如下的李雅普诺夫函数，

其中，构造的函数中的c^*和dk^*均是一个正常数。

对构造的函数求分数阶导数，得到：

整理：

由gkj＝gjk,可以得到：

假设则得到：

其中，表示克罗内克积；

根据以上证明结果易知：由于矩阵g-m的特征值都是复数，因此可得出进而根据李亚普洛夫稳定性理论可知同步达到。

二、数值仿真

数值仿真以具有10个节点的三维分数阶时变耦合复杂网络为例，该复杂网络的模型如下：

选择三维的复值洛伦兹系统为节点的动力学方程，即：

其中，复杂网络中状态向量的初值表示如下：

本实施例中，所有状态向量的初值均在(0，5)间随机选取。

同步控制器中的可调参数分别取值ε＝0.02，p＝40，同步控制器的反馈增益的初值dk(0)＝4，分数阶时变耦合复杂网络的节点内的耦合矩阵为γ＝diag(1,1,1)，不确定参数矩阵δa＝diag(δa1,δa2,...,δa3),其中ai∈(1,2),i＝1,2,3.，b＝2，耦合配置矩阵为：

仿真过程中，分数阶时变耦合复杂网络中节点与同步目标间的误差曲线如图2-7所示，其中图2-4分别反映了该三维分数阶时变耦合复杂网络第一维度、第二维度和第三维度与目标同步状态的实部误差；图5-7分别反映了该三维分数阶时变耦合复杂网络第一维度、第二维度和第三维度与目标同步状态的虚部误差；

同步控制器反馈增益的变化曲线如图8所示，分数阶时变耦合复杂网络中自适应耦合强度的变化曲线如图9所示。

分析图2-7的图像可以发现，本实施提供的方法中设计的同步控制器确实可以实现分数阶时变耦合复杂网络与同步目标间达到同步状态；并且当网络同步时，如图8和图9所示，同步控制器中的反馈增益和设计的自适应耦合强度的值也趋于稳定。

实施例4

如图10所示，本实施例提供一种n维分数阶时变耦合复杂网络的同步控制装置，该同步控制装置采用如实施例1的n维分数阶时变耦合复杂网络的同步控制方法，实现n维分数阶时变耦合复杂网络中各节点与目标同步状态的节点达到同步，同步控制装置包括：同步控制器、自适应耦合强度模块以及修正模块。

其中，同步控制器为一种自适应控制器，该自适应控制器作为实现同步所需的同步控制器uk(t)。

同步控制器uk(t)的方程为：

uk(t)＝vf(η(t))-f(xk(t))-dk(t)γek(t)-bek(t),k＝1,2,...,n。

其中，dk(t)表示所述同步控制器uk(t)的反馈增益；γ＝diag(l1,l2,...,ln)＞0表示内部耦合连接矩阵；所述函数f(·)与n维分数阶时变耦合复杂网络的模型中对应的函数符号表示的函数相同；b表示一个可调节的正常数，且满足ai≤b,i＝1,2,..,n，ai为n维分数阶时变耦合复杂网络的模型中参数矩阵a＝diag(a1,a2,...,an)中的元素。

自适应耦合强度模块用于调节n维分数阶时变耦合复杂网络中时变耦合强度c(t)；

自适应耦合强度c(t)的自适应律的表达式如下：

其中，表示对t求α次分数阶导数的标记；ε表示一个可调的正常数，表示投影同步误差ek(t)的共轭转置，γ＝diag(l1,l2,...,ln)＞0表示内部耦合连接矩阵，,gkj表示耦合配置矩阵g＝(gkj)∈r^n×n中的元素；其满足

修正模块用于将设计的同步控制器和自适应耦合强度模块引入到n维分数阶时变耦合复杂网络的模型中，实现所述n维分数阶时变耦合复杂网络中的节点与目标同步状态的节点达到同步。

实施例5

本实施例提供一种n维分数阶时变耦合复杂网络的同步控制终端，该同步控制终端包括存储器、处理器以及存储在存储器上并可在处理器上运行的计算机程序，处理器执行程序时实现如实施例1的n维分数阶时变耦合复杂网络的同步控制方法的步骤。

实施例6

本实施例提供了一种复杂网络在图像加密中的应用，本实施例中通过如实施例1的n维分数阶时变耦合复杂网络的同步控制方法实现复杂网络中各节点与目标同步状态达到同步，然后应用目标同步状态及与其达到同步的n维分数阶时变耦合复杂网络，完成对图像进行加密和解密的操作。

其中，如图11所示，图像的加密过程如下：

(1a)利用目标同步状态中节点的状态变量产生混沌信号，提取混沌信号的实部作为加密序列，提取混沌信号的虚部作为置乱序列；

(2a)对原始图像进行序列化处理，得到像素矩阵；

(3a)利用置乱序列对像素矩阵进行置乱操作，得到置乱像素矩阵；

(4a)利用加密序列对置乱像素矩阵进行加密运算，得到加密像素矩阵；

(5a)对加密像素矩阵进行反序列化处理得到加密图像。

如图11所示，加密图像的解密过程如下：

(1b)由经同步控制器同步后的n维分数阶时变耦合复杂网络产生同步混沌信号，提取同步混沌信号的实部作为解密序列，提取同步混沌信号的虚部作为反置乱序列；

(2b)对获取的加密图像进行序列化处理得到加密像素矩阵；

(3b)利用解密序列对加密像素矩阵进行解密运算得到置乱像素矩阵；

(4b)利用反置乱序列对置乱像素矩阵进行反置乱操作，得到像素矩阵；

(5b)对像素矩阵进行反序列化处理得到原始图像。

其中，加密序列和解密序列为完全同步的相同序列；置乱序列和反置乱序列为完全同步的相同序列；解密运算为加密运算的逆运算；反置乱操操作为置乱操作的逆操作。

以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。