一种智能零售机的多目标温度优化控制方法

本发明属于无人零售领域，具体涉及一种智能零售机的多目标温度优化控制方法。

技术背景

智能零售机是一种无人监管的自助购买商品的机器，商品经供应商提供暂时存放在智能零售机中，智能零售机需要为商品提供合适的环境，以满足保存需求，尤其是对食品类商品，其保鲜要求较高，商家不仅要尽可能长地延长保鲜时长，而且希望尽可能多的节约零售机能耗、降低运维成本，以达到提高经济效益的目标，然而现有的智能零售机温度控制方法很难满足这种多目标的需求。

自2016年出现“新零售”的概念后，各种形式的无人零售如春笋般冒了出来。各类智能零售机虽展示形式不同，但针对其研究的目的大都离不开增加商品存放时长、降低成本、提高遍及度。智能零售机作为典型的现代智能装备，更是未来新零售发展的重中之重，有望引领第三次新零售革命。目前的智能零售机由于数据管理体系的不完善和控制方法的不足，导致对其内部对于温度的控制只能采用粗放型的控制方法，不能对食品保鲜和装备节能等目标进行相容性控制，即在保鲜条件较好的情况下，不可避免地会大幅提高装备能耗、在降低能耗时，又不可避免地会降低保鲜效果，且这两者又间接性地影响到商品的销售量，无法达到总体目标最优。

技术实现要素：

为了克服现有技术的不足，为解决智能零售机运行过程中出现的食品保鲜、节能、经济效益三者目标无法兼顾的情况，提出一种智能零售装备的多目标温度优化控制方法。

本发明为了解决技术问题提供如下的技术方案：

一种智能零售机的多目标温度优化控制方法，所述方法包括如下步骤：

(1)依据外部环境温度、装备内部设定温度两个决策变量，满足约束条件下构建多目标适宜温度模型，获取适宜温度解集，包括如下步骤：

多目标适宜温度模型:

式中的n是指将一天中从9点到20点划分成n个相同的时间区块，不同的k值分别代表不同时间区块的下标；式中tin(k)为该时间区块的装备内部温度，tmin为食品保鲜温度下限约束，tmax为食品保鲜温度上限约束，en(k)为该时间区块的智能零售机能耗，emax为单位时间能耗上限约束，sal(k)为该时间区块的单一智能零售机销售额，smin为单位时间销售额下限约束；

将外部环境温度用x表示、装备内部设定温度用y表示，在外部环境温度保持不变的情况下，改变装备内部设定温度，同时满足食品保鲜温度约束，形成多组(x,y)元素组，分别采集不同组(x,y)情况下的不同时间区块智能零售机能耗、销售额，将其代入多目标适宜温度模型，如果满足模型约束条件，则将该组(x,y)归入适宜温度解集，如果不满足模型约束条件，则丢弃该组(x,y)；

在内部设定温度不变的情况下，测定不同时间段下的外部环境温度，从而也形成多组(x,y)元素组，同样采集不同组(x,y)情况下的不同时间区块智能零售机能耗、销售额，将其代入多目标适宜温度模型，如果满足模型约束条件，则将该组(x,y)归入适宜温度解集，如果不满足模型约束条件，则丢弃该组(x,y)；

(2)确定针对商品保鲜时长、装备能耗、销售额的多目标最优温度解，过程如下：

2.1，将m组的(x,y)按照非支配关系排序，每一层人为标定适应度值；

2.2，通过聚合、交叉、重组产生下一代集合w，集合大小为l；

2.3，将第n代的集合wn和第一代集合p合并生成集合r，将集合r进行非支配排序，产生一系列优化解fi，(i＝0,1,…)，并计算拥挤度；

2.4，把优化解fi放到第n+1代集合pn+1中；

2.5，判断：若pn+1中元素组的个数等于l，则让n加1，进而判断是否是最优温度解，如果是最优温度解，则输出该组解，否则进入步骤1；若pn+1中元素组的个数小于l，则让i加1，进入2.4；若pn+1中元素组的个数大于l，则对fi中的元素组的拥挤度进行排序，将较好的温度解保留下来，使得pn+1中元素组的个数等于l，再让n加1，进而判断是否是最优温度解，如果是最优温度解，则输出该组解，否则进入步骤2.1；

输出得到的多目标最优温度解，从而获取在不同外部环境温度下的装备内部设定温度值，用压缩机调控内部温度为该设定值即可。

本发明具有如下有益效果：将智能零售机运行过程需要满足的食品保鲜、装备节能、经济效益三个目标进行相容性控制，在满足食品保鲜要求的同时，又降低了能耗、提高了经济效益，实现了综合效益最优的最终目标。

附图说明

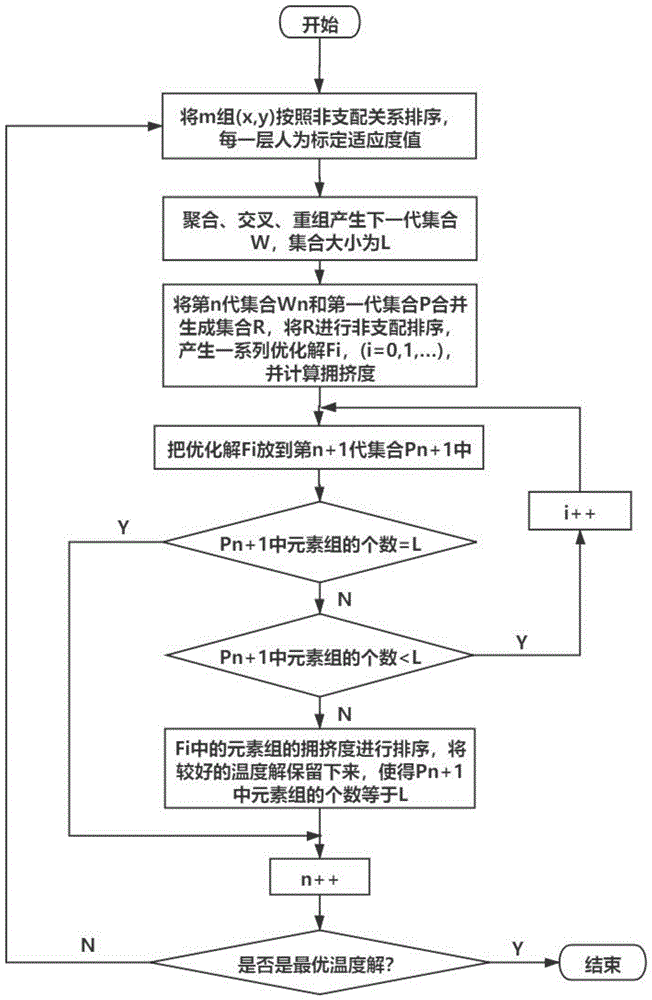
图1是本发明中多目标温度优化算法的流程图。

具体实施方式

以下结合附图和具体实施例对本发明作具体的介绍。

参照图1，一种智能零售机的多目标温度优化控制方法，所述方法包括如下步骤：

(1).依据外部环境温度、装备内部设定温度两个决策变量，满足约束条件下构建多目标适宜温度模型，获取适宜温度解集；

多目标适宜温度模型:

式中的n是指将一天中从9点到20点划分成n个相同的时间区块，不同的k值分别代表不同时间区块的下标；式中tin(k)为该时间区块的装备内部温度，tmin为食品保鲜温度下限约束，tmax为食品保鲜温度上限约束，en(k)为该时间区块的智能零售机能耗，emax为单位时间能耗上限约束，sal(k)为该时间区块的单一智能零售机销售额，smin为单位时间销售额下限约束；

将外部环境温度用x表示、装备内部设定温度用y表示，在外部环境温度保持不变的情况下，改变装备内部设定温度，同时满足食品保鲜温度约束，形成多组(x,y)元素组，分别采集不同组(x,y)情况下的不同时间区块智能零售机能耗、销售额，将其代入多目标适宜温度模型，如果满足模型约束条件，则将该组(x,y)归入适宜温度解集，如果不满足模型约束条件，则丢弃该组(x,y)；

在内部设定温度不变的情况下，测定不同时间段下的外部环境温度，从而也形成多组(x,y)元素组，同样采集不同组(x,y)情况下的不同时间区块智能零售机能耗、销售额，将其代入多目标适宜温度模型，如果满足模型约束条件，则将该组(x,y)归入适宜温度解集，如果不满足模型约束条件，则丢弃该组(x,y)；

当适宜温度解集中(x,y)元素组到达m时，停止采集，从而获得该适宜温度解集；

(2).确定针对商品保鲜时长、装备能耗、销售额的多目标最优温度解，过程如下：

2.1，将m组的(x,y)按照非支配关系排序，每一层人为标定适应度值；

2.2，通过聚合、交叉、重组产生下一代集合w，集合大小为l；

2.3，将第n代的集合wn和第一代集合p合并生成集合r，将集合r进行非支配排序，产生一系列优化解fi，(i＝0,1,…)，并计算拥挤度；

2.4，把优化解fi放到第n+1代集合pn+1中；

2.5，判断：若pn+1中元素组的个数等于l，则让n加1，进而判断是否是最优温度解，如果是最优温度解，则输出该组解，否则进入步骤1；若pn+1中元素组的个数小于l，则让i加1，进入2.4；若pn+1中元素组的个数大于l，则对fi中的元素组的拥挤度进行排序，将较好的温度解保留下来，使得pn+1中元素组的个数等于l，再让n加1，进而判断是否是最优温度解，如果是最优温度解，则输出该组解，否则进入2.1；

输出得到的多目标最优温度解，从而获取在不同外部环境温度下的装备内部设定温度值，用压缩机调控内部温度为该设定值即可。

进而可以获取在不同外部环境下所对应的最优装备内部设定温度值，在现实操作的过程中，只需要通过一个闭环系统，借助压缩机将装备内部温度稳定在最优装备内部设定温度值上下即可，从而实现了延长商品保鲜时长、降低智能零售机能耗、提高销售额的综合目标最优。