一种基于最小费用最大流的无人机任务分配方法与流程

本发明属于无人机在执行任务前的任务分配技术领域，尤其涉及一种基于最小费用最大流的无人机任务分配方法。

背景技术：

尽管无人机技术在不断的发展，飞行时间越来越长，但无人机的能耗仍是一个挑战。

在执行任务过程中，考虑到无人机的能源有限并且在不断的消耗中以及回收问题，无人机需要频繁返回补给点进行能源与物资的补充。现有研究多令无人机执行任务后返回出发点进行补给，这将无人机的活动范围限制在出发点周围，导致无人机无法执行较远距离的任务，限制了无人机的利用率。综上，由于无人机存储的能源有限，如何在考虑无人机能源限制的前提下，为无人机分配远距离的任务，扩大无人机的活动范围成为了主要的技术问题。

技术实现要素：

发明目的：本发明所要解决的技术问题是针对现有技术的不足，提供一种基于最小费用最大流的无人机任务分配方法，能够在有限的能源的前提下，在已知区域中提前规划无人机的飞行路径，减少无人机能源的消耗，完成远距离任务，防止无人机因为能源不足而无法完成任务或无法回收。

为了解决上述技术问题，本发明公开了一种基于最小费用最大流的无人机任务分配方法，包括如下步骤：

步骤1，定义任务区域内共有n个不同的任务目标构成集合l＝{l1,l2,···,ln},每个任务只需执行一次；任务区域内共有m个不同的无人机基站构成集合s＝{s1,s2,···,sm},其中无人机基站sm定义为存储着无人机以及无人机的充电设备的补给点，无人机能在任意一个无人机基站内补充能源；任务区域内有一架准备执行任务的无人机u(为了简化，假设不考虑无人机起飞降落时以及飞行中受到自然因素影响的能耗，无人机的能耗能等价为无人机的飞行距离)，在能源充满的前提下，无人机u的最长飞行距离为初始化无人机的初始停靠无人机基站为su；

步骤2，根据任务区域内的任务与无人机基站构建一个相应的最小费用最大流模型；

步骤3，将完成的任务数量建模为流量，利用步骤2中构建的最小费用最大流模型，将任务区域内的任务和无人机基站划分为若干个“起飞无人机基站-任务集合-降落无人机基站”组合；

步骤4，将步骤3中得到的“起飞无人机基站-任务集合-降落无人机基站”组合中能够顺序执行的“起飞无人机基站-任务集合-降落无人机基站”组合构建为一条初始路径i；

步骤5，若初始路径i包含所有步骤3得到的“起飞无人机基站-任务集合-降落无人机基站”组合，则初始路径i即为无人机执行所有任务的最终路径f；否则将步骤3得到的且未被初始路径i包含的“起飞无人机基站-任务集合-降落无人机基站”组合记为候选“起飞无人机基站-任务集合-降落无人机基站”组合，构成集合cls＝{c1,c2,···}。依次为集合cls中每一个候选“起飞无人机基站-任务集合-降落无人机基站”组合cj在初始路径i中寻找最佳插入点，并将cj插入最佳插入点处。当集合cls为空时，初始路径i即为无人机执行所有任务的无人机的最终路径f。

作为本发明的一种优选方案，步骤2所述最小费用最大流模型的构建如下：

(1)构建最小费用最大流模型的节点

1)添加源节点s与终点节点t作为辅助节点。

2)添加无人机基站集合节点作为一级节点。

每一个无人机基站集合节点代表一个无人机基站集合，每一个无人机基站集合由两个无人机基站构成，这两个无人机基站可以相同也可以不同。m个不同的无人机基站能构成个不同的无人机基站集合，记为其中无人机基站集合sug可表示为sug＝{sk1,sk2}，g＝1，2，···,其中sk1表示无人机在一次飞行任务中的起飞无人机基站，sk2表示无人机一次飞行任务中的降落无人机基站。

3)添加任务集合节点作为二级节点。

对于无人机基站集合sug，若sk1与sk2不同，则sk1与sk2以及所有任务点可以构成一个完全无向连通图若sk1与sk2相同，则先将sk1与sk2视为为不同的点，但它们之间的距离为0，且所有任务点到sk1的距离与到sk2的距离相同，再将sk1与sk2以及所有任务点可以构成一个完全无向连通图中每条边的权值为两点间的距离，利用深度优先算法可以获得中从sk1到sk2所有可能的路径，以及路径对应的总距离。其中总距离大于的路径将被剔除，并且对于执行相同任务但任务执行顺序不同的所有路径，只留下总距离最短的那条。剩下的每一条路径中的所有任务都构成一个任务集合。

每一个任务集合节点代表一个任务集合，假设所有无人机基站对应的任务集合的总个数为p，那么模型中共有p个不同的任务集合构成集合lu＝{lu1,lu2,···,lup}，任务集合lup可表示为lup＝{lp1,lp2,···},p＝1,2,···,p,其中lp1，lp2等表示任务集合lup包含的任务。

4)添加任务节点作为三级节点。每一个任务节点表示l中的一个任务，共有n个任务节点。

(2)构建最小费用最大流模型的边

1)添加从源节点出发的边

源节点s与每个无人机基站集合节点之间都存在边。源节点s与无人机基站集合节点之间的边的容量均为n，费用均为0。

2)添加从无人机基站集合节点出发的边

每个无人机基站集合节点与其对应的任务集合节点之间都存在边，即无人机基站集合sug节点有多少个对应的任务集就有多少条边从无人机基站集合sug节点出发。每一条边连接一个无人机基站集合和一个任务集合，可以构成一个“起飞无人机基站-任务集合-降落无人机基站”(sls)组合，所有“起飞无人机基站-任务集合-降落无人机基站”组合构成集合ls＝{ls1,ls2,···,lsp}，其中组合lsp表示为lsp＝{sug,lup},g＝1,2，···,p＝1，2，···,p。当组合lsp作为一次飞行任务时，无人机需要从无人机基站sk1起飞，执行完lup中的所有任务后降落在无人机基站sk2，无人机完成飞行任务lsk的飞行距离已由深度优先算法获得，记作d(lsp)。因此，无人机基站集合sug与任务集合lup之间的边的容量为|lup|，费用为d(lsp)。

3)添加从任务集合节点出发的边

每个任务集合节点p仅会与任务集合中包含的任务对应的任务节点间存在边，即一共有|lup|条边从任务集合节点lup节点出发。任务集合节点与任务节点之间的边的容量均为1，费用均为0。

4)添加从任务节点出发的边

每个任务节点与终点节点t之间都存在边。任务节点与终点节点t之间边的容量均为1，费用均为0。

作为本发明的一种优选方案，步骤3包括：

(1)构建相应的最小费用最大流模型g＝(v,e,$,w)。

(2)初始化无人机u的初始停靠无人机基站为su。

(3)将完成的任务数量建模为流量，基于最小费用最大流模型，获得最小费用最大流模型中费用最小的“起飞无人机基站-任务集合-降落无人机基站”组合的集合，具体步骤如下：

1)初始化可行流f为零流，此时可行流f的费用0。

2)初始化costmin为包含飞行距离最小的“起飞无人机基站-任务集合-降落无人机基站”组合lsmin在内的流fmin对应的的费用最小的“起飞无人机基站-任务集合-降落无人机基站”组合的集合的总费用

获得包含若干个“起飞无人机基站-任务集合-降落无人机基站”组合的可行流f^*对应的费用最小的“起飞无人机基站-任务集合-降落无人机基站”组合的集合的费用$f*的步骤如下：

a)易知可行流f^*的费用$f*为所有已选“起飞无人机基站-任务集合-降落无人机基站”组合的费用之和；

b)选择剩余的流网络gf*中费用最小的增广路径p^*，p^*对应的“起飞无人机基站-任务集合-降落无人机基站”组合记为lsp′。

c)将增广路径p^*加入到可行流f^*中，$f*＝$f*+d(lsp′)。如果在剩余的流网络gf中仍存在增广路径则返回b)；否则返回$f*；。

3)通过循环对ls中“起飞无人机基站-任务集合-降落无人机基站”组合lsi按飞行距离从小到大的顺序执行步骤d)至f)，以得到流网络g中费用最小的“起飞无人机基站-任务集合-降落无人机基站”组合的集合：

d)获得一个“起飞无人机基站-任务集合-降落无人机基站”lsi。

e)如果lsi中的所有任务都未被选中，那么将lsi对应的从源节点s到终点节点t的路径作为增广路径加入到可行流f中，回到d)；否则执行f)。

f)将可行流f中所有与lsi包含的任务冲突的所选任务回撤，以及与回撤任务对应的已选任务集与无人机基站集回撤，得到可行流ftemp；通过步骤a)到c)获得可行流ftemp对应的费用最小的“起飞无人机基站-任务集合-降落无人机基站”组合的集合的费用令若则令f＝ftemp，返回d)；否则直接返回d)。

4)若有部分任务不在f中，则针对未被选择的任务ln，将ln依次插入3)中选中的每个“起飞无人机基站-任务集合-降落无人机基站”组合，重新计算插入后组合的飞行距离，并与插入前的飞行距离相减得到插入任务前后的飞行距离差δcost。ln将插入δcost最小的“起飞无人机基站-任务集合-降落无人机基站”组合中，该组合的飞行距离也变为插入后的飞行距离。若不论ln插入到任意“起飞无人机基站-任务集合-降落无人机基站”组合后得到的飞行距离都大于则将ln与离ln最近的无人机基站构建一个新的“起飞无人机基站-任务集合-降落无人机基站”组合。

作为本发明的一种优选方案，步骤4所述初始路径i的构成方法如下：

(1)判断步骤3得到的“起飞无人机基站-任务集合-降落无人机基站”组合中是否存在一个组合，它的起飞无人机基站或降落无人机基站中任意一个是无人机u的初始停靠无人机基站su。若不存在这样的组合，则用su来替换离su最近的任务所在“起飞无人机基站-任务集合-降落无人机基站”组合中的起飞无人机基站或降落无人机基站。

(2)将所有能够顺序执行“起飞无人机基站-任务集合-降落无人机基站”组合构建为一条初始路径，记为i＝{i1，i2，···}。具体步骤如下：

1)初始化初始路径i为空。

2)对于每一个被选中的“起飞无人机基站-任务集合-降落无人机基站”组合中的每个组合lsk进行循环判断：

若sk1＝sk2＝su，则将lsk直接插入到i中；

若sk1＝su，sk2≠su(或sk2＝su,sk2≠su)，则将sk1(或sk2)作为lsk的起飞无人机基站，将lsk中插入到i中，令su＝sk2(su＝sk1)；

若sk1≠su且sk2≠su，则不将lsk中插入到i中。

作为本发明的一种优选方案，步骤5所述将“候选起飞无人机基站-任务集合-降落无人机基站”组合cj插入初始路径i的具体方法如下：

候选“起飞无人机基站-任务集合-降落无人机基站”组合cj插入初始路径i时有三种不同情况，插入点可以是初始路径i的开头，结尾以及两个相邻的“起飞无人机基站-任务集合-降落无人机基站”组合中间。cj的起飞无人机基站记作sj1，cj的降落无人机基站记作sj2。具体解释如下：

(1)插入初始路径i的开头。

用sz表示初始路径i的第一个“起飞无人机基站-任务集合-降落无人机基站”组合i1的起飞无人机基站，即sz＝si11。

若sj1＝sj2＝sz，那么cj一定已经在初始路径i中。

若sj1＝sz且sj1≠sj2，那么将sj1作为cj的起始基站，把cj插入到初始路径i的开头，并将i1的起飞无人机基站替换为sj2。插入cj后的初始路径i总飞行距离可以表示为：

其中d(i∨pcj)表示将cj插入到i的指定插入位置p后i的总飞行距离，d(cj)和d(i1)分别代表cj和i1的总飞行距离，表示将i1中的无人机基站sz替换为无人机基站sj2后的i1飞行距离。若sj2＝sz且sj1≠sj2时，将sj2将作为cj的起始无人机基站，sj1将作为cj的降落无人机基站插入初始路径i，cj中所有任务的执行顺序需要颠倒。插入cj后的初始路径i总飞行距离的计算与(1)同理。

若sj1≠sz且sj2≠sz时，sj1与sj2可能相同也可能不同。分别用公式(2)(3)计算用sz替换sj1和用sz替换sj2后再将cj插入初始路径i后的总飞行距离，并且i1的起飞无人机基站被替换为cj中未替换的无人机基站。之后利用公式(4)选出飞行距离最小的作为最终的插入方案。

其中和表示将cj插入到初始路径i指定插入位置p后i的总飞行距离，上标sj1和sj2分别表示cj中被sz替换的无人机基站。

(2)插入初始路径i的结尾。

用sz表示初始路径i的最后一个“起飞无人机基站-任务集合-降落无人机基站”组合iend的降落无人机基站，即sz＝siend。

若sj1＝sz且sj1≠sj2，那么sj1将作为cj的起始无人机基站，sj2将作为cj的降落无人机基站，把cj插入到初始路径i的末尾。插入cj后的初始路径i总飞行距离可以表示为：

d(i∨pcj)＝d(i)+d(cj)(5)

若sj2＝sz且sj1≠sj2时，将sj2将作为cj的起始无人机基站，sj1将作为cj的降落无人机基站插入到初始路径i末尾，cj中所有任务的执行顺序需要颠倒。用公式(5)计算插入cj后的初始路径i总飞行距离。

若sj1≠sz且sj2≠sz时，sj1与sj2可能相同也可能不同。分别用公式(6)(7)计算用sz替换sj1和用sz替换sj2后再将cj插入初始路径i末尾后的总飞行距离。之后利用公式(8)选出飞行距离最小的作为最终的插入方案。

(3)插入初始路径i中两个相邻的“起飞无人机基站-任务集合-降落无人机基站”组合中间。

用sz表示插入点前一个“起飞无人机基站-任务集合-降落无人机基站”组合i(γ-1)的降落无人机基站和后一个“起飞无人机基站-任务集合-降落无人机基站”组合iγ的起飞无人机基站，即sz＝si(γ-1)2＝siγ1。

若sj1＝sj2＝sz，那么cj直接插入到指定位置，用公式(5)表示插入cj后的初始路径i的总飞行距离。

若sj1＝sz且sj1≠sj2，那么sj1将作为cj的起始无人机基站，sj2将作为cj的降落无人机基站，把cj插入到插入点，并且iγ的起飞无人机基站被替换为sj2。插入cj后的初始路径i总飞行距离可以表示为：

若sj2＝sz且sj1≠sj2，将sj2将作为cj的起始无人机基站，sj1将作为cj的降落无人机基站插入到插入点，cj中所有任务的执行顺序需要颠倒，并且iγ的起飞无人机基站被替换为sj1。插入cj后的初始路径i总飞行距离的计算与(9)同理。

若sj1≠sz且sj2≠sz时，sj1与sj2可能相同也可能不同。分别用公式(2)(3)计算用sz替换sj1和用sz替换sj2后再将cj插入到插入点后的总飞行距离，并且iγ的起飞无人机基站应该被替换为cj中未替换的无人机基站。之后利用公式(4)选出飞行距离最小的作为最终的插入方案。

有益效果：

提供了一种基于最小费用最大流的无人机任务分配方法。使无人机能够在有限的能源的前提下，在已知区域中提前规划无人机的飞行路径，从而有效减少无人机能源的消耗，较好的完成远距离任务，防止无人机因为能源不足而无法完成任务或无法回收的问题。拓展了无人机的任务距离，扩大了无人机的活动范围。

附图说明

下面结合附图和具体实施方式对本发明做更进一步的具体说明，本发明的上述和/或其他方面的优点将会变得更加清楚。

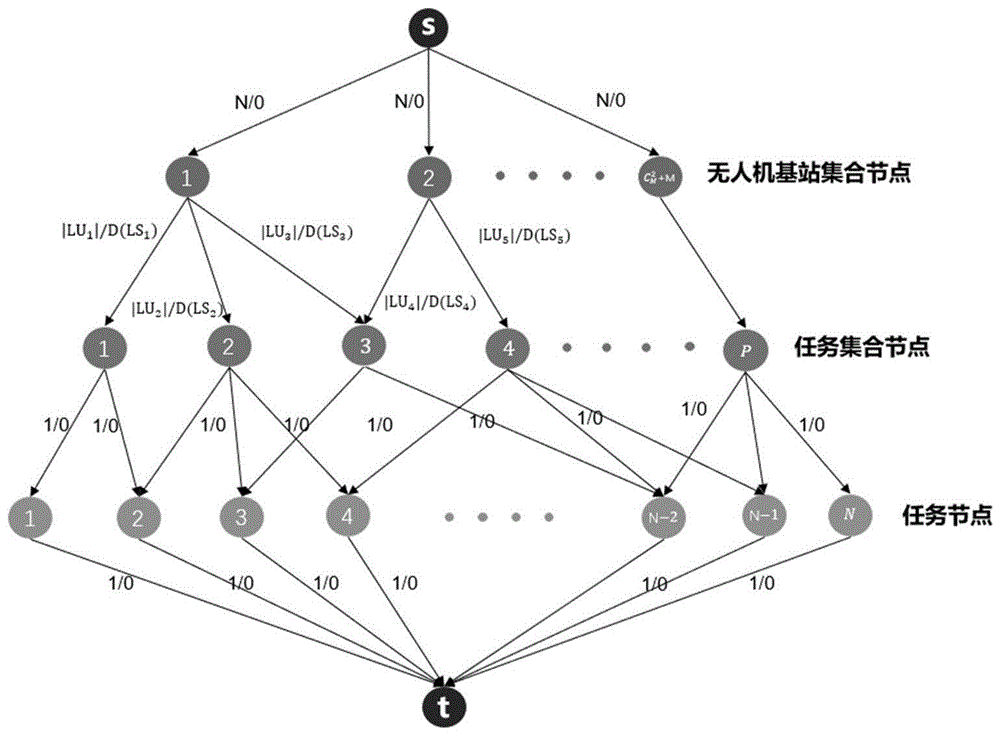
图1是将任务区域内的任务与无人机基站划分为若干个“无人机基站-任务集-无人机基站”集合使用的最小费用最大流模型。

图2是本发明实施例提供的一种基于最小费用最大流的无人机任务分配方法的流程示意图。

图3是将候选“起飞无人机基站-任务集合-降落无人机基站”组合插入初始路径时的第一种情况。

图4是将候选“起飞无人机基站-任务集合-降落无人机基站”组合插入初始路径时的第二种情况。

图5是将候选“起飞无人机基站-任务集合-降落无人机基站”组合插入初始路径时的第三种情况。

具体实施方式

下面详细描述本发明的实施方式，所述实施方式的示例在附图中示出。下面通过参考附图描述的实施方式是示例性的，仅用于解释本发明，而不能解释为对本发明的限制。

图1为将任务区域内的任务与无人机基站划分为若干个“无人机基站-任务集-无人机基站”集合使用的最小费用最大流模型。最小费用最大流模型构成的流网络是一个有向图g＝(v,e,$,w)，其中v表示图中的节点，e表示图中的边，$表示边的费用，w表示边的容量。有向图g中每条边都具有容量，流量和费用三个属性。构建最小费用最大流模型对应的流网络g＝(v,e,$,w)的具体步骤如下：

(1)构建系统模型

1)任务区域内有n个不同的任务目标构成集合l＝{l1,l2,···,ln}，每个目标只需要执行一次。

2)任务区域内有m个不同的无人机基站构成集合s＝{s1,s2,···,sm}，其中无人机基站sm定义为存储着无人机以及无人机的充电设备的补给站，无人机可在任意一个无人机基站内补充能源。

3)任务区域内有一架准备执行任务的无人机u(为了简化，假设不考虑无人机起飞降落时以及飞行中受到自然因素影响的能耗，无人机的能耗能等价为无人机的飞行距离)，在能源充满的前提下，无人机u的最长飞行距离为

(1)构建最小费用最大流模型的节点

1)添加源节点s与终点节点t作为辅助节点。

2)添加无人机基站集合节点作为一级节点。

每一个无人机基站集合节点代表一个无人机基站集合，每一个无人机基站集合由两个无人机基站构成，这两个无人机基站可以相同也可以不同。m个不同的无人机基站能构成个不同的无人机基站集合，记为其中无人机基站集合sug可表示为sug＝{sk1,sk2},g＝1,2,···,其中sk1表示无人机在一次飞行任务中的起飞无人机基站，sk2表示无人机一次飞行任务中的降落无人机基站。

3)添加任务集合节点作为二级节点。。

对于无人机基站集合sug，若sk1与sk2不同，则sk1与sk2以及所有任务点可以构成一个完全无向连通图若sk1与sk2相同，则先将sk1与sk2视为不同的点，但它们之间的距离为0，且所有任务点到sk1的距离与到sk2的距离相同，再将sk1与sk2以及所有任务点可以构成一个完全无向连通图中每条边的权值为两点间的距离，利用深度优先算法可以获得中从sk1到sk2所有可能的路径，以及路径对应的总距离。其中总距离大于的路径将被剔除，并且对于执行相同任务但任务执行顺序不同的所有路径，只留下总距离最短的那条。剩下的每一条路径中的所有任务都构成一个任务集合。

每一个任务集合节点代表一个任务集合，假设所有无人机基站对应的任务集合的总个数为p，那么模型中共有p个不同的任务集合构成集合lu＝{lu1,lu2,···,lup}，任务集合lup可表示为lup＝{lp1,lp2,···},p＝1,2,···,p,其中lp1，lp2等表示任务集合lup包含的任务。

4)添加任务节点作为三级节点。每一个任务节点表示l中的一个任务，共有n个任务节点。

(2)构建最小费用最大流模型的边

1)添加从源节点出发的边

源节点s与每个无人机基站集合节点之间都存在边。源节点s与无人机基站集合节点之间的边的容量均为n，费用均为0。

2)添加从无人机基站集合节点出发的边

每个无人机基站集合节点与其对应的任务集合节点之间都存在边，即无人机基站集合sug节点有多少个对应的任务集就有多少条边从无人机基站集合sug节点出发。每一条边连接一个无人机基站集合和一个任务集合，可以构成一个“起飞无人机基站-任务集合-降落无人机基站”(sls)组合，所有“起飞无人机基站-任务集合-降落无人机基站”组合构成集合ls＝{ls1,ls2,···,lsp}，其中组合lsp表示为lsp＝{sug,lup},g＝1,2,···,p＝1,2,···,p。当组合lup作为一次飞行任务时，无人机需要从无人机基站sk1起飞，执行完lup中的所有任务后降落在无人机基站sk2，无人机完成飞行任务lsk的飞行距离已由深度优先算法获得，记作d(lsp)。因此，无人机基站集合sug与任务集合lup之间的边的容量为|lup|，费用为d(lsp)。

3)添加从任务集合节点出发的边

每个任务集合节点p仅会与任务集合中包含的任务对应的任务节点间存在边，即一共有|lup|条边从任务集合节点lup节点出发。任务集合节点与任务节点之间的边的容量均为1，费用均为0。

4)添加从任务节点出发的边

每个任务节点与终点节点t之间都存在边。任务节点与终点节点t之间边的容量均为1，费用均为0。

如图2所示，本发明提出一种基于最小费用最大流的无人机任务分配方法，其具体步骤如下：

(1)初始化无人机u的初始停靠无人机基站su。

(2)构建相应的最小费用最大流模型。

(3)将完成的任务数量建模为流量，基于最小费用最大流模型，将任务区域内的任务与无人机基站划分为若干个“起飞无人机基站-任务集合-降落无人机基站”组合，具体步骤如下：

(1)构建相应的最小费用最大流模型g＝(v,e,$,w)。

(2)初始化无人机u的初始停靠无人机基站为su。

(3)将完成的任务数量建模为流量，基于最小费用最大流模型，获得最小费用最大流模型中费用最小的“起飞无人机基站-任务集合-降落无人机基站”组合的集合，具体步骤如下：

1)初始化可行流f为零流，此时可行流f的费用0。

2)初始化costmin为包含飞行距离最小的“起飞无人机基站-任务集合-降落无人机基站”组合lsmin在内的流fmin对应的的费用最小的“起飞无人机基站-任务集合-降落无人机基站”组合的集合的总费用

获得包含若干个“起飞无人机基站-任务集合-降落无人机基站”组合的可行流f^*对应的费用最小的“起飞无人机基站-任务集合-降落无人机基站”组合的集合的费用$f*的步骤如下：

a)易知可行流f^*的费用$f*为所有已选“起飞无人机基站-任务集合-降落无人机基站”组合的费用之和。

b)选择剩余的流网络gf*中费用最小的增广路径p^*，p^*对应的“起飞无人机基站-任务集合-降落无人机基站”组合记为lsp′。

c)将增广路径p^*加入到可行流f^*中，$f*＝$f*+d(lsp′)。如果在剩余的流网络gf中仍存在增广路径则返回b)；否则返回$f*。

3)通过循环对ls中“起飞无人机基站-任务集合-降落无人机基站”组合lsi按飞行距离从小到大的顺序执行步骤d)至f)，以得到流网络g中费用最小的“起飞无人机基站-任务集合-降落无人机基站”组合的集合：

d)获得一个“起飞无人机基站-任务集合-降落无人机基站”lsi。

e)如果lsi中的所有任务都未被选中，那么将lsi对应的从源节点s到终点节点t的路径作为增广路径加入到可行流f中，回到d)；否则执行f)。

f)将可行流f中所有与lsi包含的任务冲突的所选任务回撤，以及与回撤任务对应的已选任务集与无人机基站集回撤，得到可行流ftemp；通过步骤a)到c)获得可行流ftemp对应的费用最小的“起飞无人机基站-任务集合-降落无人机基站”组合的集合的费用令若则令f＝ftemp，返回d)；否则直接返回d)。

4)若全部任务都在f中，则执行(4)；否则针对未被选择的任务ln，将ln依次插入3)中选中的每个“起飞无人机基站-任务集合-降落无人机基站”组合，重新计算插入后组合的飞行距离，并与插入前的飞行距离相减得到插入任务前后的飞行距离差δcost。ln将插入δcost最小的“起飞无人机基站-任务集合-降落无人机基站”组合中，该组合的飞行距离也变为插入后的飞行距离。若不论ln插入到任意“起飞无人机基站-任务集合-降落无人机基站”组合后得到的飞行距离都大于则将ln与离ln最近的无人机基站构建一个新的“起飞无人机基站-任务集合-降落无人机基站”组合。

(4)判断所有得到的“起飞无人机基站-任务集合-降落无人机基站”组合中是否存在一个组合，它的起飞无人机基站或降落无人机基站中任意一个是初始停靠无人机基站su。若不存在这样的组合，则用su来替换离su最近的任务所在“起飞无人机基站-任务集合-降落无人机基站”组合中的起飞基站或降落基站。调整完成后，将所有能够顺序执行“起飞无人机基站-任务集合-降落无人机基站”组合构建为一条初始路径，记为i＝{i1,i2,···}。具体步骤如下：

1)初始化初始路径i为空。

2)对于每一个被选中的“起飞无人机基站-任务集合-降落无人机基站”组合中的每个组合lsk进行循环判断：

若sk1＝sk2＝su，则将lsk直接插入到i中；

若sk1＝su，sk2≠su(或sk2＝su，sk2≠su)，则将sk1(或sk2)作为lsk的起飞无人机基站，将lsk中插入到i中，令su＝sk2(su＝sk1)；

若sk1≠su且sk2≠su，则不将lsk中插入到i中。

(5)若初始路径i包含(3)中所有得到“起飞无人机基站-任务集合-降落无人机基站”组合，则初始路径i就是无人机执行所有任务的最终路径f；否则将由(3)得到的未被初始路径i包含的“起飞无人机基站-任务集合-降落无人机基站”组合被记为候选“起飞无人机基站-任务集合-降落无人机基站”组合，构成集合cls＝{c1,c2,···}。依次将集合cls中每一个候选“起飞无人机基站-任务集合-降落无人机基站”组合cj插入到初始路径i中的每一个插入点，插入点可以是初始路径i的开头，结尾以及两个相邻的“起飞无人机基站-任务集合-降落无人机基站”组合中间。通过比较将候选“起飞无人机基站-任务集合-降落无人机基站”组合插入指定插入点后的总飞行距离，选择总飞行距离最小的插入点作为cj的最佳插入点，并将cj插入最佳插入点。当集合cls为空时，初始路径i就是无人机执行所有任务的最终路径f。最终路径f中的每一个“起飞无人机基站-任务集合-降落无人机基站”组合都是无人机的一次飞行任务，无人机通过顺序执行最终路径f中的每一个飞行任务，能够执行完所有任务。

图3，图4以及图5是将候选“起飞无人机基站-任务集合-降落无人机基站”组合cj插入初始路径i时三种不同情况。cj的起飞无人机基站记作sj1，cj的降落无人机基站记作sj2。具体解释如下：

1)插入初始路径i的开头。

插入位置如图3所示。

用sz表示初始路径i的第一个“起飞无人机基站-任务集合-降落无人机基站”组合i1的起飞无人机基站，即sz＝si11。

若sj1＝sj2＝sz，那么cj一定已经在初始路径i中。

若sj1＝sz且sj1≠sj2，那么将sj1作为cj的起始基站，把cj插入到初始路径i的开头，并将i1的起飞无人机基站替换为sj2。插入cj后的初始路径i总飞行距离可以表示为：

其中d(i∨pcj)表示将cj插入到i的指定插入位置p后i的总飞行距离，d(cj)和d(i1)分别代表cj和i1的总飞行距离，表示将i1中的无人机基站sz替换为无人机基站sj2后的i1飞行距离。若sj2＝sz且sj1≠sj2时，将sj2将作为cj的起始无人机基站，sj1将作为cj的降落无人机基站插入初始路径i，cj中所有任务的执行顺序需要颠倒。插入cj后的初始路径i总飞行距离的计算与(1)同理。

若sj1≠sz且sj2≠sz时，sj1与sj2可能相同也可能不同。分别用公式(2)(3)计算用sz替换sj1和用sz替换sj2后再将cj插入初始路径i后的总飞行距离，并且i1的起飞无人机基站被替换为cj中未替换的无人机基站。之后利用公式(4)选出飞行距离最小的作为最终的插入方案。

其中和表示将cj插入到初始路径i指定插入位置p后i的总飞行距离，上标sj1和sj2分别表示cj中被sz替换的无人机基站。

2)插入初始路径i的结尾。

插入位置如图4所示。用sz表示初始路径i的最后一个“起飞无人机基站-任务集合-降落无人机基站”组合iend的降落无人机基站，即sz＝siend2。

若sj1＝sz且sj1≠sj2，那么sj1将作为cj的起始无人机基站，sj2将作为cj的降落无人机基站，把cj插入到初始路径i的末尾。插入cj后的初始路径i总飞行距离可以表示为：

d(i∨pcj)＝d(i)+d(cj)(5)

若sj2＝sz且sj1≠sj2时，将sj2将作为cj的起始无人机基站，sj1将作为cj的降落无人机基站插入到初始路径i末尾，cj中所有任务的执行顺序需要颠倒。用公式(5)计算插入cj后的初始路径i总飞行距离。

若sj1≠sz且sj2≠sz时，sj1与sj2可能相同也可能不同。分别用公式(6)(7)计算用sz替换sj1和用sz替换sj2后再将cj插入初始路径i末尾后的总飞行距离。之后利用公式(8)选出飞行距离最小的作为最终的插入方案。

3)插入初始路径i中两个相邻的“起飞无人机基站-任务集合-降落无人机基站”组合中间。

插入位置如图5所示。用sz表示插入点前一个“起飞无人机基站-任务集合-降落无人机基站”组合i(γ-1)的降落无人机基站和后一个“起飞无人机基站-任务集合-降落无人机基站”组合iγ的起飞无人机基站，即sz＝si(γ-1)2＝siγ1。

若sj1＝sj2＝sz，那么cj直接插入到指定位置，用公式(5)表示插入cj后的初始路径i的总飞行距离。

若sj1＝sz且sj1≠sj2，那么sj1将作为cj的起始无人机基站，sj2将作为cj的降落无人机基站，把cj插入到插入点，并且iγ的起飞无人机基站被替换为sj2。插入cj后的初始路径i总飞行距离可以表示为：

若sj2＝sz且sj1≠sj2，将sj2将作为cj的起始无人机基站，sj1将作为cj的降落无人机基站插入到插入点，cj中所有任务的执行顺序需要颠倒，并且iγ的起飞无人机基站被替换为sj1。插入cj后的初始路径i总飞行距离的计算与(9)同理。

若sj1≠sz且sj2≠sz时，sj1与sj2可能相同也可能不同。分别用公式(2)(3)计算用sz替换sj1和用sz替换sj2后再将cj插入到插入点后的总飞行距离，并且iγ的起飞无人机基站应该被替换为cj中未替换的无人机基站。之后利用公式(4)选出飞行距离最小的作为最终的插入方案。

本发明提供了一种基于最小费用最大流的无人机任务分配方法，具体实现该技术方案的方法和途径很多，以上所述仅是本发明的具体实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。本实施例中未明确的各组成部分均可用现有技术加以实现。