一种基于递推子空间辨识的自适应逆控制AGV转速控制方法

一种基于递推子空间辨识的自适应逆控制agv转速控制方法
技术领域
1.本发明涉及agv调速技术领域，更具体地说，涉及一种基于递推子空间辨识的自适应逆控制agv转速控制方法。


背景技术：

2.全向agv的导向轮多采用麦克纳姆轮或球形轮，在轨迹跟踪过程中，自动导引小车的控制模型通常不会考虑万向轮从动对agv主体的作用，由于忽略了这一影响因素，控制系统可能出现不稳定状态。多数研究者建模时将agv假设为刚体，其运动过程未考虑因车体负载不均或磨损导致的轮子半径变化问题，而agv实际运动过程中，由于负载不均导致左右轮形变和大小不一都会对轨迹跟踪控制的精度造成较大的影响。
3.采用机理建模时难以确定模型结构和模型参数，因此目前更多的研究集中于数据驱动的黑箱模型或半机理半数据的灰箱模型。agv调速系统是对agv进行控制的主要系统，其动态性能直接影响到运输系统的经济性和安全性。为了合理地整定agv控制器参数、准确地分析跟踪系统的稳定特性，均需要研究agv运动学系统的详细模型。实时辨识是获取模型的一种有效手段。agv调速系统是具有非最小相位、非线性的控制系统，应根据其自身特点、不同运行方式和工况条件等对其进行实时动态的建模、辨识。子空间辨识法是一类直接估计线性时不变状态变量模型的黑盒建模方法，其具有无需非线性迭代优化、无需参数初始化、解算速度快、实现对系统矩阵参数的一致估计的优点。自适应控制是一种能够自动修正控制规律及控制器特性、以适应对象和扰动的动态特性变化的控制方法。自适应逆控制是典型的自适应控制方式之一。为此在agv路径跟踪系统建模时考虑车体参数的变化，实现自适应参数的控制是agv动态路径跟踪控制的关键。


技术实现要素：

4.本发明的目的在于克服现有技术中的缺点与不足，提供一种基于递推子空间辨识的自适应逆控制agv转速控制方法，该agv转速控制方法能很好适应agv参数变化的调速系统设计，有效克服控制对象的非线性，并有效抑制外部扰动，有利于改善对agv路径跟踪控制的品质和精度。
5.为了达到上述目的，本发明通过下述技术方案予以实现：一种基于递推子空间辨识的自适应逆控制agv转速控制方法，其特征在于：利用递推子空间辨识算法获得agv运动学系统的等效逆模型的基本参数；在此基础上利用自适应逆控制法进行agv转速自适应逆控制器的设计，并将agv运动学系统的等效逆模型作为agv转速自适应逆控制器的传递函数，实现对agv转速的自适应跟踪控制。
6.包括以下步骤：
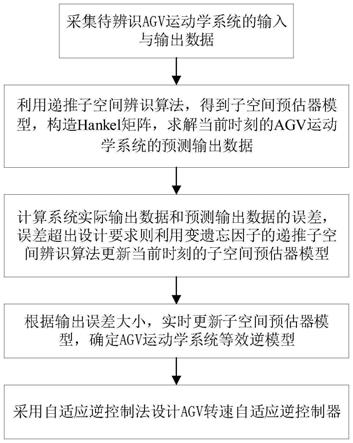
7.步骤1，采集待辨识agv运动学系统的输入数据和输出数据；
8.步骤2，利用递推子空间辨识算法，得到子空间预估器模型，构造当前时刻输入数据和输出数据的hankel矩阵，求解当前时刻的agv运动学系统的预测输出数据；
9.步骤3，根据agv的控制动作，确定下一时刻的实际输出数据，计算系统实际输出数据和预测输出数据的误差，若超过容许误差，则利用增加变遗忘因子的递推子空间辨识算法更新当前时刻的子空间预估器模型，得到下一时刻的子空间预估器模型，否则不更新当前时刻的子空间预估器模型；
10.步骤4，重复步骤2和3，实时更新子空间预估器模型，确定agv运动学系统的等效逆模型；
11.步骤5，采用自适应逆控制法设计agv转速自适应逆控制器，将agv转速作为目标信号，将步骤4得到的agv运动学系统的等效逆模型作为控制器的传递函数；将目标信号输入agv转速自适应逆控制器得到控制信号，再用控制信号激励agv，实现对agv转速的自适应跟踪控制。
12.步骤1中，采用agv的位置作为agv运动学系统的输入数据，采用agv轮子的速度作为agv运动学系统的输出数据。
13.步骤2中，所述利用递推子空间辨识算法，得到子空间预估器模型是指：采用递推子空间辨识算法在线获得agv运动学系统的输入数据u和输出数据y，实现对agv运动学系统矩阵[a,b,c,d]的在线递推估计，agv运动学系统矩阵[a,b,c,d]为子空间预估器模型：
[0014]
线性离散时不变系统形式为：
[0015]
x
k+1
＝ax
k
+bu
k
+ke
k
ꢀꢀ
(1)
[0016]
y
k
＝cx
k
+du
k
+e
k
ꢀꢀ
(2)
[0017]
其中u
k
∈r
l
为系统的输入测量值，y
k
∈r
m
为系统的输出测量值，x
k
∈r
n
为系统的过程状态，e
k
∈r
m
为平稳、零均值的白噪声新息序列，k为稳定的状态kalman增益，a，b，c，d为相对应维数的agv运动学系统矩阵，a为n
×
n维系统矩阵，b为n
×
r维控制矩阵，c为m
×
n维输出矩阵，d为m
×
r维前馈矩阵。
[0018]
步骤2中，所述构构造当前时刻输入数据和输出数据的hankel矩阵，求解当前时刻的agv运动学系统的预测输出数据是指：
[0019]
设定采样时刻k∈{1,2,
…
,2i+j
‑
1}，构造系统输入u
k
的i行j列hankel矩阵：
[0020][0021][0022]
其中，下标p和f分别代表“过去”和“未来”，也表示hankel矩阵的维数；β为指数加权遗忘因子，满足0<β<1；同理，输出y
k
的hankel矩阵y
p
、y
f
由(1)
‑
(2)迭代可以得到递推的预测输出：
[0023][0024]
其中，γ
i
∈r
im*n
为广义可观测矩阵，和为下三角矩阵，分别
表示：
[0025][0026][0027][0028]
y
f
的最优预测输出可由的行空间到的行空间的正交投影得到：
[0029][0030]
其中w
p
为过去的输入输出数据矩阵，即l
w
、l
u
分别表示状态和确定输入子空间预估器矩阵，可通过如下的qr分解和svd分解求得；
[0031]
利用qr分解：
[0032][0033]
其中r为下三角阵，q为正交矩阵。实施正交投影(9)，可得：
[0034][0035]
其中上角标表示moore
‑
penrose广义逆，将得到的l
w
和l
u
用于预测控制器的设计；
[0036]
考虑如下的预测控制目标代价函数：
[0037][0038]
其中n2为预测时域，n
u
为控制时域，λ为控制作用加权系数，r
t+k
为未来时刻t+k的设定值；
[0039]
的第1列用于预测未来输出值，采用增量型形式表示为：
[0040][0041]
作为agv运动学系统的预测输出数据。
[0042]
步骤3中，所述根据agv的控制动作，确定下一时刻的实际输出数据，计算系统实际
输出数据和预测输出数据的误差，若超过容许误差，则利用增加变遗忘因子的递推子空间辨识算法更新当前时刻的子空间预估器模型，得到下一时刻的子空间预估器模型，否则不更新当前时刻的子空间预估器模型是指：
[0043]
根据agv加入的控制动作u
k+1
，确定k+1时刻的实际输出数据y
k+1
，计算实际输出数据y
k+1
和式(13)中预测输出数据的误差，若该误差超过容许误差，则利用变遗忘因子的递推子空间辨识算法更新子空间预估器模型，得到agv运动学系统矩阵[a,b,c,d]作为下一时刻的子空间预估器模型：
[0044]
设定在t+1时刻，新的输入输出对{u(t+1),y(t+1)}已知，构造下述数据向量：
[0045][0046][0047]
则当t+1时刻获取新的数据后，更新的数据hankel矩阵为：
[0048][0049]
对更新的数据矩阵做qr分解，并通过一系列givens旋转变换，对分解得到的下三角阵r进行svd分解即可从求解获得系统矩阵；
[0050]
由(6)可知，系统矩阵c的估计值可由下式直接获得：
[0051][0052]
系统矩阵a则可通过求解下述线性方程获得：
[0053][0054]
实际上，的估计值则可描述为下述优化问题的解：
[0055][0056]
其中因此系统矩阵a可通过递推最小二乘法求解，其递推算法如下：
[0057][0058][0059][0060]
其中γ(t)为随时间变化的遗忘因子，且0<γ(t)<1，常取接近1的常数；p(t)为逆
相关矩阵；
[0061]
系统矩阵b和d包含在矩阵中，为得到其估计值，须从式(5)中消去项；
[0062]
定义矩阵为子空间的正交补投影因子：
[0063][0064]
式(5)两边同时左乘右乘得：
[0065][0066]
其中
[0067][0068][0069][0070]
m
l
∈r；即有：
[0071][0072]
在每一时刻用最近的估计值代替则和的估计值可以类似于式(26)～(28)递推求解。
[0073]
步骤4中，agv运动学系统的等效逆模型则为实时更新的agv运动学系统矩阵[a,b,c,d]。
[0074]
与现有技术相比，本发明具有如下优点与有益效果：
[0075]
1、本发明基于递推子空间辨识的自适应逆控制agv转速控制方法，该agv转速控制方法能很好适应agv参数变化的调速系统设计，有效克服控制对象的非线性，并有效抑制外部扰动，有利于改善对agv路径跟踪控制的品质和精度。
[0076]
2、本发明基于递推子空间辨识的自适应逆控制agv转速控制方法能够为建立高精度的agv运动学系统模型打下坚实基础，为agv运动学系统的控制系统设计提供依据和参考，工程实用性较高。
附图说明
[0077]
图1是本发明基于递推子空间辨识的自适应逆控制agv转速控制方法的流程图；
[0078]
图2是本发明agv转速自适应逆控制器的示意图；
[0079]
图3是本发明agv转速自适应逆控制器的控制原理图；
[0080]
图4(1)和图4(2)是本发明利用递推子空间辨识算法辨识agv运动学系统的参数a1、a2仿真效果图；
[0081]
图5(1)和图5(2)是本发明利用递推子空间辨识算法辨识agv运动学系统的参数
b0、b1仿真效果图；
[0082]
图6是本实施例agv采用的模型图。
具体实施方式
[0083]
下面结合附图与具体实施方式对本发明作进一步详细的描述。
[0084]
实施例
[0085]
如图1至图6所示，本发明基于递推子空间辨识的自适应逆控制agv转速控制方法是这样的：利用递推子空间辨识算法获得agv运动学系统的等效逆模型的基本参数；在此基础上利用自适应逆控制法进行agv转速自适应逆控制器的设计，并将agv运动学系统的等效逆模型作为agv转速自适应逆控制器的传递函数，实现对agv转速的自适应跟踪控制。
[0086]
具体包括以下步骤：
[0087]
步骤1，采集待辨识agv运动学系统的输入数据和输出数据，在agv监控平台采集至少100组实验数据，其中，采用agv的位置作为agv运动学系统的输入数据，采用agv轮子的速度作为agv运动学系统的输出数据。
[0088]
步骤2，利用递推子空间辨识算法，得到子空间预估器模型，构造当前时刻输入数据和输出数据的hankel矩阵，求解当前时刻的agv运动学系统的预测输出数据。
[0089]
采用递推子空间辨识算法在线获得agv运动学系统的输入数据u和输出数据y，实现对agv运动学系统矩阵[a,b,c,d]的在线递推估计，agv运动学系统矩阵[a,b,c,d]为子空间预估器模型：
[0090]
线性离散时不变系统形式为：
[0091]
x
k+1
＝ax
k
+bu
k
+ke
k
ꢀꢀ
(1)
[0092]
y
k
＝cx
k
+du
k
+e
k
ꢀꢀ
(2)
[0093]
其中u
k
∈r
l
为系统的输入测量值，y
k
∈r
m
为系统的输出测量值，x
k
∈r
n
为系统的过程状态，e
k
∈r
m
为平稳、零均值的白噪声新息序列，k为稳定的状态kalman增益，a，b，c，d为相对应维数的agv运动学系统矩阵，a为n
×
n维系统矩阵，b为n
×
r维控制矩阵，c为m
×
n维输出矩阵，d为m
×
r维前馈矩阵。
[0094][0095][0096]
为保证系统的可辨识性以及收敛性分析要求，假定系统满足下述条件：
[0097]
1)(a，b)能控，(a，c)能观测，系统为最小实现。
[0098]
2)外部输入u与噪声e不相关，且u满足充分激励条件。
[0099]
设定采样时刻k∈{1,2,
…
,2i+j
‑
1}，构造系统输入u
k
的i行j列hankel矩阵：
[0100][0101][0102]
其中，下标p和f分别代表“过去”和“未来”，也表示hankel矩阵的维数；β为指数加权遗忘因子，满足0<β<1；同理，输出y
k
、噪声e
k
的hankel矩阵y
p
、y
f
、e
p
、e
f
也有类似定义。输出y
k
的hankel矩阵y
p
、y
f
由(1)
‑
(2)迭代可以得到递推的预测输出：
[0103][0104]
其中，γ
i
∈r
im*n
为广义可观测矩阵，和为下三角矩阵，分别表示：
[0105][0106][0107][0108]
y
f
的最优预测输出可由的行空间到的行空间的正交投影得到：
[0109][0110]
其中w
p
为过去的输入输出数据矩阵，即l
w
、l
u
分别表示状态和确定输入子空间预估器矩阵，可通过如下的qr分解和svd分解求得；
[0111]
利用qr分解：
[0112]
[0113]
其中r为下三角阵，q为正交矩阵。实施正交投影(9)，可得：
[0114][0115]
其中上角标表示moore
‑
penrose广义逆，将得到的l
w
和l
u
用于预测控制器的设计；
[0116]
考虑如下的预测控制目标代价函数：
[0117][0118]
其中n2为预测时域，n
u
为控制时域，λ为控制作用加权系数，r
t+k
为未来时刻t+k的设定值；
[0119]
的第1列用于预测未来输出值，采用增量型形式表示为：
[0120][0121]
作为agv运动学系统的预测输出数据。
[0122]
其中
[0123][0124]
f＝[i
m
ꢀ…ꢀ
i
m
]
t
ꢀꢀ
(15)
[0125][0126]
由l
w
构造：
[0127][0128]
其中1≤k≤n2。将(13)代入(12)，求取控制律，得到
[0129][0130]
只需将δu
f
的第一个值δu
t
作为控制输入，下一时刻再重新计算控制输入，因此t时刻的控制输入为：
[0131]
u
t
＝u
t
‑1+δu
t
ꢀꢀ
(19)。
[0132]
步骤3，根据agv的控制动作，确定下一时刻的实际输出数据，计算系统实际输出数据和预测输出数据的误差，若超过容许误差，则利用增加变遗忘因子的递推子空间辨识算法更新当前时刻的子空间预估器模型，得到下一时刻的子空间预估器模型，否则不更新当前时刻的子空间预估器模型：
[0133]
根据agv加入的控制动作u
k+1
，确定k+1时刻的实际输出数据y
k+1
，计算实际输出数据y
k+1
和式(13)中预测输出数据的误差，若该误差超过容许误差，则利用变遗忘因子的递推子空间辨识算法更新子空间预估器模型，得到agv运动学系统矩阵[a,b,c,d]作为下一时刻的子空间预估器模型：
[0134]
设定在t+1时刻，新的输入输出对{u(t+1),y(t+1)}已知，构造下述数据向量：
[0135][0136][0137]
则当t+1时刻获取新的数据后，更新的数据hankel矩阵为：
[0138][0139]
对更新的数据矩阵做qr分解，并通过一系列givens旋转变换，对分解得到的下三角阵r进行svd分解即可从求解获得系统矩阵；
[0140]
由(6)可知，系统矩阵c的估计值可由下式直接获得：
[0141][0142]
系统矩阵a则可通过求解下述线性方程获得：
[0143][0144]
实际上，的估计值则可描述为下述优化问题的解：
[0145][0146]
其中因此系统矩阵a可通过递推最小二乘法求解，其递推算法如下：
[0147][0148][0149][0150]
其中γ(t)为随时间变化的遗忘因子，且0<γ(t)<1，常取接近1的常数；p(t)为逆相关矩阵；
[0151]
系统矩阵b和d包含在矩阵中，为得到其估计值，须从式(5)中消去项；定义矩阵为子空间的正交补投影因子：
[0152][0153]
式(5)两边同时左乘右乘得：
[0154][0155]
其中
[0156][0157][0158][0159]
m
l
∈r；即有：
[0160][0161]
在每一时刻用最近的估计值代替则和的估计值可以类似于式(26)～(28)递推求解。
[0162]
步骤4，重复步骤2和3，实时更新子空间预估器模型，确定agv运动学系统的等效逆模型；agv运动学系统的等效逆模型则为实时更新的agv运动学系统矩阵[a,b,c,d]。
[0163]
步骤5，采用自适应逆控制法设计agv转速自适应逆控制器，将agv转速作为目标信号，将步骤4得到的agv运动学系统的等效逆模型作为控制器的传递函数；将目标信号输入agv转速自适应逆控制器得到控制信号，再用控制信号激励agv，实现对agv转速的自适应跟踪控制。
[0164]
根据现代控制理论，系统的传递函数阵和状态空间表达式之间的转换公式g)s)＝c(si
‑
a)
‑1b+d，可通过agv运动学系统状态空间表达式得到agv运动学系统的传递函数：
[0165][0166]
本实施例对本发明方法得到的agv运动学系统进行系统辨识仿真实验，原agv运动学系统的参数a1＝
‑
1.971，a2＝0.971，b0＝0.6007，b1＝0.6126。在k＝30时刻，agv运动学系统参数变化为a1＝
‑
0.97，a2＝0.6702，b0＝0.195，b1＝2.0187，验证递推子空间辨识算法效果佳。结果表明递推子空间辨识算法在计算的50步内能够准确辨识出系统参数，证实了辨识算法的有效性。
[0167]
本实施例采用的agv的模型如图6所示。
[0168]
上述实施例为本发明较佳的实施方式，但本发明的实施方式并不受上述实施例的限制，其他的任何未背离本发明的精神实质与原理下所作的改变、修饰、替代、组合、简化，均应为等效的置换方式，都包含在本发明的保护范围之内。