一种基于三角函数加减速控制的直接速度过渡光顺方法

1.本发明涉及一种数控加工路径光顺方法，特别涉及一种基于三角函数加减速控制的直接速度过渡光顺方法。


背景技术：

2.目前，数控机床是现代加工中十分重要的一环，能够实现高速、高精、高效的加工。在数控加工过程中，刀具轨迹的光顺以及柔性的加减速成为了提高精度和效率的重点。由g01代码点组成的微线段已被广泛用于复杂几何部件的加工当中，微线段的优点是能够很好的描述表达几何部件的形状，但是在微线段的连接处，会存在路径方向的不连续以及曲率的不连续性，这会导致在加工过程中会有较大的振动，影响了加工精度和效率。为此，进行刀具轨迹的拐角局部光顺对提高加工质量和效率起着重要作用。在现有的局部过渡的算法中，“连续微线段高速加工数控系统路径与速度前瞻规划算法研究[d]﹒浙江大学，2018”文献中对几种常见的局部过渡的算法进行了系统的介绍，还提出了基于优化最大转角速度的局部过渡方法。像这种先对刀具轨迹进行优化，再对优化好的刀具轨迹进行加减速规划的方法，我们称之为“两步法”过渡。两步法过渡的算法复杂程度跟优化的刀具轨迹相关；所以要想获得较高的路径连续性，必然会增大算法的复杂程度，影响了加工的实时性。同时这种传统两步法的线性与几何过渡方案对拐角处的运动学性能以及平滑度提升有限。


技术实现要素：

[0003]
本发明为解决公知技术中存在的技术问题而提供一种基于三角函数加减速控制的直接速度过渡光顺方法。
[0004]
本发明为解决公知技术中存在的技术问题所采取的技术方案是：一种基于三角函数加减速控制的直接速度过渡光顺方法，读取加工代码点位坐标，设原始加工路径是由连续点位连接的微线段组成，由点位坐标计算微线段长度以及相邻微线段间的夹角；将每个微线段的加工过程依照加速度函数划分为多段，使两个相邻微线段拐角的过渡阶段处于前一段微线段的减速阶段和后一段微线段的加速阶段，采用sin(2x)作为加加速度的基函数建立微线段加工过程加减速模型，设置最大加速度及加减速参数；根据最大允许加工误差求解微线段拐角的交叠混合过渡时间及过渡起始时间，进行运动合成，从而获得光顺优化后的加工路径。
[0005]
进一步地，设每个微线段的起点速度和终点速度为0，将每个微线段的加工过程划分为七段；其中第1、3、5、7段为变加速阶段，第2、6段为匀变速阶段，第4段为匀速阶段，其中第4段的速度最大。
[0006]
进一步地，设j(t)为加加速度，设a(t)为加速度，设t
i
为第i段的时间，设τ
i
为第i段内所处时刻，设t
i
为第i阶段的临界时间，其中i为段号，i＝1,2,
…
,7；建立如下微线段加工过程加减速模型：
[0007][0008][0009][0010]
式中，k为加速度参数，a
act
为最大加速度。
[0011]
进一步地，在第t1阶段，当加工时刻时，加加速度达到最大；设最大加加速度为j
max
；使变加速段的时间相等，均为t
j
；匀变速段的时间也相等，均为t
a
；设经历t1、t2两段加速过程后，达到的临界速度为f
cri
；设设微线段的最大进给速度为v
t
；则各变加速段和匀加速段的时间如下：
[0012][0013][0014]
根据速度对象对称性，加速部分距离s
a
及减速部分距离s
d
为：
[0015][0016]
则匀速段时间为：
[0017][0018]
式中，t
i
,(i＝1,2,
…
,7)为第i阶段的时间，l为微线段长度，v
c
为匀速段的进给速度。
[0019]
进一步地，设第n微线段的过渡线段长度为ε1，设第n+1微线段的过渡线段长度为
ε2，设第n微线段与第n+1微线段的混合过渡时间为t
r
；设第n微线段与第n+1微线段的近似过渡最大误差与混合过渡时间t
r
之间存在如下函数关系：
[0020][0021]
τ
i
＝t
r
‑
t
n,i
‑1,(i＝1,2,3)；
[0022][0023]
式中，t
n,i
,(i＝1,2,3)为第n微线段第i阶段的结束时间；t
n,i
,(i＝1,2,3)为第n微线段第i阶段的时间；a
n,act
为第n微线段的最大加速度；v
n,1
为第n微线段第1阶段结束时的速度值；v
n,2
为第n微线段第2阶段结束时的速度值；s
n
(t)为第n微线段t时间内的位移；
[0024][0025]
τ
i
＝t
r
‑
t
n+1,i
‑1,(i＝1,2,3)；
[0026][0027]
式中，t
n+1,i
,(i＝1,2,3)为第n+1微线段第i阶段的结束时间；t
n+1,i
,(i＝1,2,3)为第n+1微线段第i阶段的时间；a
n+1,act
为第n+1微线段的最大加速度；v
n+1,1
为第n+1微线段第1阶段结束时的速度值；v
n+1,2
为第n+1微线段第2阶段结束时的速度值；s
n+1
(t)为第n+1微线段t时间内的位移；
[0028][0029]
式中，θ为第n微线段和第n+1微线段间的夹角，ε为近似过渡最大误差。
[0030]
进一步地，设f(t
r
)＝ε
‑
ε
max
为二分法求解函数；
[0031]
令f(t
r
)＝ε
‑
ε
max
＝0，其中，ε
max
为加工最大允许误差，ε为近似过渡最大误差；通过二分法求解，求得过渡时间t
r
。
[0032]
进一步地，设第n微线段的速度规划时间为第n微线段与第n
‑
1微线段的过渡时间为t
trn,n
‑1，第n微线段与第n+1微线段的过渡时间为t
trn,n+1
，第n
‑
1微线段的减速段时间为t
n
‑
1,d
，第n+1微线段的加速段时间为t
n+1,a
，设ε
trn,n
‑1为第n微线段与第n
‑
1微线段的过渡误差，ε
trn,n+1
为第n微线段与第n+1微线段的过渡误差，设ε
max
为加工最大允许误差；若第n段微
线段过渡时间满足条件t
n
‑
1,d
>t
trn,n
‑1,且t
n+1,a
>t
trn,n+1
，过渡误差满足条件ε
trn,n
‑1＜ε
max
,ε
trn,n+1
＜ε
max
，则定义该段为受限段，增大该段的过渡时间。
[0033]
进一步地，设第n微线段与第n
‑
1微线段的原始过渡时间为设第n微线段与第n+1微线段的过渡时间为设t
ov
‑1为第n微线段与第n
‑
1微线段的交叠时间，设t
ov+1
为第n微线段与第n+1微线段的交叠时间，使第n段的过渡时间按如下公式增大：
[0034][0035][0036]
式中，为第n微线段与第n
‑
1微线段的修正过渡时间，为第n微线段与第n+1微线段的修正过渡时间；
[0037]
设ε为近似过渡最大误差；ε
max
为加工最大允许误差；设t
ov
为平均交叠时间；设f(t
r
)＝ε
‑
ε
max
为二分法求解函数；
[0038]
令t
ov+1
＝t
ov
‑1＝t
ov
；
[0039]
令f(t
r
)＝ε
‑
ε
max
＝0；
[0040]
将修正的过渡时间代入公式f(t
r
)＝ε
‑
ε
max
＝0，通过二分法求解，求解出平均交叠时间t
ov
。
[0041]
进一步地，设任意连续两段微线段中，第一段微线段减速段起始点为p1；设第一段微线段的终止点为p2；设第二段微线段的加速段终止点为p3；设为的单位向量；设为的单位向量；设p1点位置坐标为w1，设第一、二微线段过渡路径合成后，在t时刻合成过渡路径中对应的点位坐标为w
t
，其中则有：
[0042][0043]
式中：为第一微线段的总规划时间；t
r
为过渡时间；t
r
为中间变量，s1(t)为第一微线段的位移函数；s2(t)为第二微线段的位移函数。
[0044]
进一步地，根据最大允许加工误差求解微线段拐角的混合过渡时间；当某一段微线段的混合过渡时间小于相邻微线段的加速或减速阶段时间时，解除混合过渡时间约束，增大微线段两侧的混合过渡时间；
[0045]
设任意连续三段微线段中，第一段微线段减速段起始点为p1，设第一段微线段的终止点为p2，设第二段微线段的加速段终止点为p3，设第三段微线段的加速段终止点为p4，设为的单位向量；设为的单位向量；设为的单位向量；设p1点位置坐标为w1，设第一、二微线段过渡路径合成后，在t时刻合成过渡路径中对应的点位坐标为w
t
，若连续三段微线段中的第二段微线段为受限段，增加第二段微线段两侧的混合过渡时间，进行第一、二、三段微线段的过渡路径合成；其中则有：
[0046][0047]
式中：和分别对应为第一微线段和第二微线段的总规划时间；t
r,1
为第一微线段和第二微线段的过渡时间；t
ov
为平均交叠时间；t
r,1
和t
r,2
为中间变量，s1(t)为第一微线段的位移函数；s2(t)为第二微线段的位移函数；s3(t)为第三微线段的位移函数。
[0048]
本发明具有的优点和积极效果是：由于各轴运动符合三角函数加减速运动特性，拐角处运动合成后，以及具有很高的运动连续性。本发明避免了连续微线段加工过程中，在拐点出的频繁加减速，从而提高了机床加工过程中的精确性，以及改善了拐点出的运动学性能，提高了加工效率。与传统的插入几何曲线的过渡方式不同，本方法采用的合成拐点处插补路径的方法，避免了插入几何曲线的复杂算法过程，同时保证了加工过程中运动的高阶连续性，同时对于过短的微线段进行了过渡优化，提升了加工过程中的平稳性以及加工效率。本发明可实现一步过渡，能够保证在高运动连续性下，实现三轴运动拐点出的平滑过渡，解决了传统数控加工过程中连续为线段的几何不连续性问题，与两步过渡方法相比，降低了算法的复杂程度同时提高了拐角处的加工效率。
附图说明
[0049]
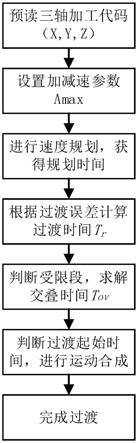
图1是本发明的一种工作流程简图。
[0050]
图2是七段式加减速曲线图。
[0051]
图3是过渡误差示意图。
[0052]
图4是时间轴插补过程图。
[0053]
图5是合成过渡路径原理图。
[0054]
图6是相邻过渡曲线交叠示意图。
[0055]
图7是加工路径示例图。
[0056]
图8是过渡路径仿真放大图。
[0057]
图2中：τ
i
,(i＝1,2,
…
,7)为各阶段的起始时刻，t
i
,(i＝1,2,
…
,7)为各阶段的终止时刻，t
i
,(i＝1,2,
…
，7)为各阶段的时间。v(t)为速度轴，a(t)为加速度轴，j(t)为加加速度轴，t为时间轴。
[0058]
图3中：任意连续两段微线段中，p1为第一微线段过渡起始点，p2为第一、二微线段的交点，p3为第二微线段的过渡终止点，ε1为第一微线段的过渡线段长度，ε2为第二微线段的过渡线段长度，ε
max
为最大过渡误差，a为第一微线段过渡起始点，o为第一、二微线段的交点，b为第二微线段的过渡终止点，θ为第一、二微线段间的转角。
[0059]
图4中：tr为混合过渡时间，t
r
为中间变量，为中间变量，为第一微线段速度规划总时间，vt为速度轴，t为时间轴。
[0060]
图5中：a为第一微线段过渡起始点，o为第一、二微线段的交点，b为第二微线段的
过渡终止点，v1为第一段线段运行速度，v2为第二段线段运行速度，s1(t1)为第一段线段t1时刻位移，s2(t
r
)为第二段线段tr时刻位移。
[0061]
图6中：任意连续三段微线段中，p1为第一微线段过渡起始点，p2为第一、二微线段的交点，p3为第二微线段的过渡终止点，p4为第三段微线段的过渡终止点，ε
tri1
为第一、二段微线段拐角的过渡误差，ε
tri2
为第二、三段微线段拐角的过渡误差，ε
ov
为对受限段的过渡时间修正后的交叠误差。
具体实施方式
[0062]
为能进一步了解本发明的发明内容、特点及功效，兹列举以下实施例，并配合附图详细说明如下：
[0063]
请参见图1至图8，本发明为解决公知技术中存在的技术问题所采取的技术方案是：一种基于三角函数加减速控制的直接速度过渡光顺方法，读取加工代码点位坐标，设原始加工路径是由连续点位连接的微线段组成，由点位坐标计算微线段长度以及相邻微线段间的夹角；将每个微线段的加工过程依照加速度函数划分为多段，使两个相邻微线段拐角的过渡阶段处于前一段微线段的减速阶段和后一段微线段的加速阶段，采用sin(2x)作为加加速度的基函数建立微线段加工过程加减速模型，设置最大加速度及加减速参数；根据最大允许加工误差求解微线段拐角的交叠混合过渡时间及过渡起始时间，进行运动合成，从而获得光顺优化后的加工路径。
[0064]
进一步地，可设每个微线段的起点速度和终点速度为0，将每个微线段的加工过程依照加速度函数划分为七段；其中第1、3、5、7段可为变加速阶段，第2、6段可为匀变速阶段，第4段可为匀速阶段，其中第4段的速度最大。可按加速度函数分为7段，依次为：第1段加加速段、第2段匀加速、第3段减加速、第4段匀速、第5段加减速、第6段匀减速、第7段减减速。确定好基本的构造函数后，就能够建立加减速模型。
[0065]
进一步地，可设j(t)为加加速度，设a(t)为加速度，设t
i
为第i段的时间，设τ
i
为第i段内所处时刻，设t
i
为第i阶段的临界时间，其中i为段号，i＝1,2,
…
,7；可建立如下微线段加工过程加减速模型：
[0066]
[0067][0068][0069]
式中，k为加速度参数，a
act
为最大加速度。
[0070]
确定了微线段加工过程加减速模型之后，可以通过积分来获得微线段加工过程速度模型v(t)以及微线段加工过程位移模型s(t)。其速度模型和位移模型如下式所示。
[0071][0072]
[0073]
其中，为加速度参数，t
i
(i＝1,3,5,7)是各阶段的时间，a
act
为最大加速度，τ
i
(i＝1,3,5,7)为各阶段内所处时刻，t
i
(i＝1,2,
…
，7)为第i阶段的临界时间,v1,v2,v3分别表示为第1、2、3阶段结束时的速度。
[0074]
进一步地，在第t1阶段，可当加工时刻时，使加加速度达到最大；可设最大加加速度为j
max
；可使变加速段的时间相等，均为t
j
；匀变速段的时间也相等，均为t
a
；设经历t1、t2两段加速过程后，达到的临界速度为f
cri
；可设设微线段的最大进给速度为v
t
；则各变加速段和匀加速段的时间可如下：
[0075][0076][0077]
根据速度对象对称性，加速部分距离s
a
及减速部分距离s
d
可为：
[0078][0079]
则匀速段时间可为：
[0080][0081]
式中，t
i
,(i＝1,2,
…
,7)为第i阶段的时间，l为微线段长度，v
c
为匀速段的进给速度。
[0082]
进一步地，可设第n微线段的过渡线段长度为ε1，设第n+1微线段的过渡线段长度为ε2，设第n微线段与第n+1微线段的混合过渡时间为t
r
；可设第n微线段与第n+1微线段的近似过渡最大误差与混合过渡时间t
r
之间存在如下函数关系：
[0083][0084]
τ
i
＝t
r
‑
t
n,i
‑1,(i＝1,2,3)；
[0085][0086]
式中，t
n,i
,(i＝1,2,3)为第n微线段第i阶段的结束时间；t
n,i
,(i＝1,2,3)为第n微线段第i阶段的时间；a
n,act
为第n微线段的最大加速度；v
n,1
为第n微线段第1阶段后速度值；
v
n,2
为第n微线段第2阶段后速度值；s
n
(t)为第n微线段t时间内的位移。
[0087][0088]
τ
i
＝t
r
‑
t
n+1,i
‑1,(i＝1,2,3)；
[0089][0090]
式中，t
n+1,i
,(i＝1,2,3)为第n+1微线段第i阶段的结束时间；t
n+1,i
,(i＝1,2,3)为第n+1微线段第i阶段的时间；a
n+1,act
为第n+1微线段的最大加速度；v
n+1,1
为第n+1微线段第1阶段后速度值；v
n+1,2
为第n+1微线段第2阶段后速度值；s
n+1
(t)为第n+1微线段t时间内的位移。
[0091][0092]
式中，θ为第n微线段和第n+1微线段间的夹角，ε为近似过渡最大误差。
[0093]
进一步地，可设f(t
r
)＝ε
‑
ε
max
为二分法的求解函数。
[0094]
可令f(t
r
)＝ε
‑
ε
max
＝0，其中，ε
max
为加工最大允许误差，ε为近似过渡最大误差；可通过二分法求解，求得过渡时间t
r
。
[0095]
进一步地，设第n微线段的速度规划时间为第n微线段与第n
‑
1微线段的过渡时间为t
trn,n
‑1，第n微线段与第n+1微线段的过渡时间为t
trn,n+1
，第n
‑
1微线段的减速段时间为t
n
‑
1,d
，第n+1微线段的加速段时间为t
n+1,a
，设ε
trn,n
‑1为第n微线段与第n
‑
1微线段的过渡误差，ε
trn,n+1
为第n微线段与第n+1微线段的过渡误差，设ε
max
为加工最大允许误差。若第n段微线段过渡时间满足条件t
n
‑
1,d
>t
trn,n
‑1,且t
n+1,a
>t
trn,n+1
，过渡误差满足条件ε
trn,n
‑1＜ε
max
,ε
trn,n+1
＜ε
max
，则定义该段为受限段，增大该段的过渡时间。
[0096]
进一步地，可设第n微线段与第n
‑
1微线段的原始过渡时间为设第n微线段与第n+1微线段的过渡时间为设t
ov
‑1为第n微线段与第n
‑
1微线段的交叠时间，设t
ov+1
为第n微线段与第n+1微线段的交叠时间，可使第n段的过渡时间按如下公式增大：
[0097][0098][0099]
式中，第n微线段与第n
‑
1微线段的修正过渡时间，为第n微线段与第n+1微线段的修正过渡时间；
[0100]
可设ε为近似过渡最大误差；ε
max
为加工最大允许误差；设t
ov
为平均交叠时间；可设f(t
r
)＝ε
‑
ε
max
为二分法求解函数；
[0101]
可令t
ov+1
＝t
ov
‑1＝t
ov
；
[0102]
可令f(t
r
)＝ε
‑
ε
max
＝0；
[0103]
可将修正的过渡时间代入公式f(t
r
)＝ε
‑
ε
max
＝0，可通过二分法求解，求解出平均交叠时间t
ov
。
[0104]
进一步地，可设任意连续两段微线段中，第一段微线段减速段起始点为p1；设第一段微线段的终止点为p2；设第二段微线段的加速段终止点为p3；设为的单位向量；设为的单位向量；设p1点位置坐标为w1，设第一、二微线段过渡路径合成后，在t时刻合成过渡路径中对应的点位坐标为w
t
，其中则可有：
[0105][0106]
式中：为第一微线段的总规划时间；t
r
为过渡时间；t
r
为中间变量，s1(t)为第一微线段的位移函数；s2(t)为第二微线段的位移函数。
[0107]
进一步地，可根据最大允许加工误差求解微线段拐角的混合过渡时间；当某一段微线段的混合过渡时间小于相邻微线段的加速或减速阶段时间时，可解除混合过渡时间约束，增大微线段两侧的混合过渡时间；
[0108]
可设任意连续三段微线段中，第一段微线段减速段起始点为p1，设第一段微线段的终止点为p2，设第二段微线段的加速段终止点为p3，设第三段微线段的加速段终止点为p4，设为的单位向量；设为的单位向量；设为的单位向量；设p1点位置坐标为w1，设第一、二微线段过渡路径合成后，在t时刻合成过渡路径中对应的点位坐标为w
t
，若连续三段微线段中的第二段微线段为受限段，可增加第二段微线段两侧的混合过渡时间，进行第一、二、三段微线段的过渡路径合成；其中则可有：
[0109][0110]
式中：和分别对应为第一微线段和第二微线段的总规划时间；t
r,1
为第一微线段和第二微线段的过渡时间；t
ov
为平均交叠时间；t
r,1
和t
r,2
为中间变量，s1(t)为第一微线段的位移函数；s2(t)为第二微线段的位移函数；s3(t)为第三微线段的位移函数。
[0111]
下面以本发明的一个优选实施例来进一步说明本发明的工作流程及工作原理：
[0112]
一种基于三角函数加减速控制的直接速度过渡光顺方法，读取xyz三轴的加工代码点位坐标，加工路径是由连续点位连接的微线段组成，由点位坐标计算微线段长度以及相邻微线段间的夹角；根据最大加速度以及加减速参数，利用7段式的三角函数加减速对微线段进行加减速规划；微线段拐角的过渡阶段处于前一段微线段的减速阶段和后一段微线段的加速阶段，根据最大允许加工误差求解微线段拐角的混合过渡时间；当某一段微线段的混合过渡时间小于相邻微线段的加速或减速阶段时，为发挥最大过渡性能，解除混合过
渡时间约束，增大微线段两端的混合过渡时间，根据最大误差求解出交叠混合过渡时间；最后判断混合过渡和交叠混合过渡状态，进行运动合成，从而获得光顺的加工路径。
[0113]
采用7段式三角函数的加减速，加加速度采用sin(2x)作为基函数建立加工路径模型，加速度也通过对加加速度积分，以sin2(x)为基函数，加速度在到达最大加速度时会保持一段时间，做匀加速运动，提高加工的进给速度。
[0114]
具体工作流程如下：
[0115]
一、读取加工代码，计算路径长度及相邻两路径间的夹角。
[0116]
读取三轴加工代码点位坐标(x,y,z)，根据公式(1)求解相邻点位p1(x1,y1,z1)到p2(x2,y2,z2)间的路径长度p1p2,p2(x2,y2,z2)到p3(x3,y3,z3)间的路径长度p2p3；根据公式(2)可计算出两路径间的夹角θ。
[0117][0118][0119]
二、建立7段式三角函数加减速模型，基于7段式三角函数加减速模型进行速度规划。
[0120]
7段式三角函数可按加速度和速度分为7段：加加速、匀加速、减加速、匀速、加减速、匀减速、减减速。确定好基本的构造函数后，就能够建立加减速模型。
[0121]
1.确定7段式三角函数模型。
[0122]
加加速度采用sin(2x)作为基函数进行建立模型，加速度也通过对加加速度积分，以sin2(x)为基函数，加速度在到达最大加速度时会保持一段时间，做匀加速运动，提高加工的进给效率。其加加速度函数和加速度函数入公式(3)、(4)所示。
[0123][0124]
[0125]
其中为加速度参数，t
i
(i＝1,3,5,7)是各阶段的时间，a
act
为最大加速度，τ
i
(i＝1,3,5,7)为各阶段内所处时刻，t
i
(i＝1,2,
…
，7)为第i阶段的临界时间。
[0126]
2.确定了加速度函数之后，可以通过积分来获得速度模型v(t)以及位移模型s(t)。其速度模型和位移模型如公式(5)、(6)所示。
[0127][0128][0129]
其中，为加速度参数，t
i
(i＝1,3,5,7)是各阶段的时间，a
act
为最大加速度，τ
i
(i＝1,3,5,7)为各阶段内所处时刻，t
i
(i＝1,2,
…
，7)为第i阶段的临界时间,v1,v2,v3分别表示为第1、2、3阶段结束时的速度。
[0130]
3.获取速度规划时间
[0131]
确定加减速模型之后，对预读的连续微线段进行速度规划，获得各部分的速度规划时间，确定微线段的运动过程。考虑微线段足够长的情况下，设每个微线段的起始速度为
v
s
，微线段的最大进给速度为v
t
，微线段的终点速度为v
e
，最大加速度为a
act
。在不包含前瞻功能时，默认v
s
＝v
e
＝0，则可以等到各运动段时间：
[0132]
在第1阶段，当加工时刻时，加加速度达到最大，最大加加速度表示为j
max
。令t
j
为变加速段的时间，各变加速阶段的时间可以表示为：
[0133][0134]
经历两段变加速过程后，能够达到的临界速度f
cri
为：
[0135][0136]
令t
a
为匀变速段的时间，匀加速段和匀减速段时间表示为：
[0137][0138]
根据速度对象对称性可知，加速部分距离s
a
，减速部分距离s
d
为：
[0139][0140]
匀速时间为：
[0141][0142]
式中，t
i
,(i＝1,2,
…
,7)为第i阶段的时间，l为微线段长度，v
c
为匀速段的进给速度。。
[0143]
三、设置过渡误差，确定过渡时间
[0144]
1.确定过渡距离
[0145]
确定了各规划段的时间，设定最大过渡误差ε
max
，如图3所示,ε1,ε2为过渡长度，ε
max
为最大过渡误差，θ为微线段的夹角。
[0146]
在运动过程中，a到o为第一段路径的减速段，o到b为第二段路径的加速段，由运动对称性可得：ε1＝ε2，由几何关系可得：
[0147][0148]
令s
1d
为第一段微线段的减速段距离，s
2a
为第二段微线段的加速段距离，当ε1≥s
1d
或者ε2≥s
2a
时，令ε1＝ε2＝min{s
1d
,s
2a
}。
[0149]
2.求解过渡时间
[0150]
记混合过渡时间为t
r
，已知过渡距离ε1＝ε2＝e，过渡从第一段的减速段开始，根据位移公式(6)可得：
[0151][0152]
其中，τ
i
＝t
r
‑
t
i
‑1,(i＝1,2,3)，a
act
为最大加速度，为加速度参数，t
i
(i＝1,3)是各阶段的时间，v1和v2分别为第1阶段和第2阶段后的速度值，s(t)为t时刻的位移函数。
[0153]
令其中，ε
max
为加工最大允许误差，θ为微线段的夹角。通过二分法求解，可求得过渡时间t
r
。
[0154]
四、确定受限段，求解交叠时间。
[0155]
设第n微线段的速度规划时间为第n微线段与第n
‑
1微线段的过渡时间为t
trn,n
‑1，第n微线段与第n+1微线段的过渡时间为t
trn,n+1
，第n
‑
1微线段的减速段时间为t
n
‑
1,d
，第n+1微线段的加速段时间为t
n+1,a
，设ε
trn,n
‑1为第n微线段与第n
‑
1微线段的过渡误差，ε
trn,n+1
为第n微线段与第n+1微线段的过渡误差，设ε
max
为加工最大允许误差；若第n段微线段过渡时间满足条件t
n
‑
1,d
>t
trn,n
‑1,且t
n+1,a
>t
trn,n+1
，过渡误差满足条件ε
trn,n
‑1＜ε
max
,ε
trn,n+1
＜ε
max
，则定义该段为受限段，增大该段的过渡时间。
[0156]
设第n微线段与第n
‑
1微线段的原始过渡时间为设第n微线段与第n+1微线段的过渡时间为设t
ov
‑1为第n微线段与第n
‑
1微线段的交叠时间，设t
ov+1
为第n微线段与第n+1微线段的交叠时间，使第n段的过渡时间按如下公式增大：
[0157][0158]
式中，第n微线段与第n
‑
1微线段的修正过渡时间，为第n微线段与第n+1微线段的修正过渡时间；
[0159]
设ε为近似过渡最大误差；ε
max
为加工最大允许误差；设t
ov
为平均交叠时间；设f(t
r
)＝ε
‑
ε
max
为二分法求解函数；
[0160]
令t
ov+1
＝t
ov
‑1＝t
ov
；
[0161]
令f(t
r
)＝ε
‑
ε
max
＝0；
[0162]
将修正的过渡时间代入公式f(t
r
)＝ε
‑
ε
max
＝0，通过二分法求解，求解出平均交叠时间t
ov
。
[0163]
五、进行运动合成，执行混合过渡
[0164]
1.连续两段微线段之间的混合过渡
[0165]
如图5所示，在过渡区域aob路径中，从图5点a开始，在插补第一段的路径的同时，进行第二段路径插补，将二者运动进行合成，从而获得过渡路径。设第一微线段过渡起始点为p1，设第一、二微线段的交点为p2，设第二微线段的过渡终止点为p3，设为的单位向
量；设为的单位向量；设v1为第一段线段运行速度，v2为第二段线段运行速度，设p1点位置坐标为w1，设第一、二微线段过渡路径合成后，在t时刻合成过渡路径中对应的点位坐标为w
t
，第一微线段的总规划时间为若则根据公式(6)可以知第一段路径t时刻的位移s1(t)以及第二段路径过渡区域内t时刻的位移s2(t
r
)，并得到混合过渡路径时刻的过渡位置：
[0166][0167]
其中：t
r
为过渡时间；t
r
为中间变量，s1(t)为第一微线段的位移函数；s2(t)为第二微线段的位移函数。
[0168]
2.连续三段微线段的交叠混合过渡
[0169]
当某段微线段的长度较小时，会使过渡时间受限，造成过渡效果大打折扣。当出现微线段为受限段时，进行连续三段微线的运动合成，根据公式(6)可以知第一段路径t时刻的位移s1(t)以及第二段、第三段路径过渡区域内t时刻的位移s2(t
r
)和s3(t
r
)，并得到混合过渡路径t((t1‑
t
r
)≤t≤t1)时刻的过渡位置。
[0170]
设第一段微线段减速段起始点为p1，设第一、二段微线段的交点为p2，设第二段微线段的加速段终止点为p3，设第三段微线段的加速段终止点为p4，设为的单位向量；设为的单位向量；设为的单位向量；设p1点位置坐标为w1，在t时刻合成过渡路径中对应的点位坐标为w
t
，进行第一、二、三段微线段的过渡路径合成。其中则有：
[0171][0172]
式中：和分别为第一微线段和第二微线段的总规划时间；t
r,1
为第一二段的过渡时间；t
r,1
和t
r,2
为中间变量，s1(t)为第一微线段的位移函数；s2(t)为第二微线段的位移函数；s3(t)为第三微线段的位移函数。
[0173]
至此通过混合插补的方式完成了拐角处的混合插补一步过渡。
[0174]
本发明的工作原理：针对此不足，提出了一种基于7段式三角函数加减速控制的“一步法”过渡方案。通过混合拐点处插补路径，对过短微线段进行过渡优化，获得新的平滑过渡路径，在保证高阶路径连续性与算法实时性的同时，提升连续微线段拐角处的连续性。该方法可以广泛用于三轴机床当中。
[0175]
给出三轴加工示例坐标(0，0，0)，(1，3，0)，(1.1，3，0)，(1.5，0，0)。相关的参数设置为：最大进给速度f
max
＝50mm/s,最大轴加速度为a
max
＝300mm/s2，最大加加速度为j
max
＝6000mm/s3，在直接速度混合过渡混合算法的求解过程中：设置最大允许过渡误差为：ε
max
＝
0.01mm，混合过渡误差二分求解过程中，求解精度δ＝0.001mm。
[0176]
步骤1：预读坐标位置，根据公式(1)、(2)计算第一、二微线段路径长度以及两相邻路径夹角如下：
[0177]
l1＝3.1622mm,θ1＝1.2490rad，
[0178]
l2＝0.1000mm,θ2＝1.4382rad，
[0179]
l3＝3.0265mm。
[0180]
步骤2：完成数据的预处理后，根据设定的加速度参数，对相邻两路径进行速度规划，获得规划时间。根据公式(7)、(8)、(9)、(10)、(11)获得各规划段时间，计算图2中插补规划时间。
[0181]
第一段微线段插补规划时间：t1＝0.07452s,t2＝0.00000s,t4＝0.00000s；
[0182]
第二段微线段插补规划时间：t1＝0.02357s,t2＝0.00000s,t4＝0.0000s；
[0183]
第三段微线段插补规划时间：t1＝0.07334s,t2＝0.00000s,t4＝0.00000s。
[0184]
步骤3：速度规划后，根据步骤1中计算条件，以及设定的过渡误差ε，依照公式(13)，通过二分法求解混合过渡时间。
[0185]
第一、二段微线段之间拐角的过渡时间：t
r,1
＝0.04713s；
[0186]
第二、三段微线段之间拐角的过渡时间：t
r,2
＝0.04713s。
[0187]
步骤4：判断微线段是否受限，第二段微线段满足受限条件，依公式(13)、(14)计算受限段的交叠过渡时间。
[0188]
t
ov
＝0.04713s。
[0189]
步骤5：执行混合插补过渡，若下一微线段为受限段，进行交叠混合过渡，依据公式(16)进行三段微线段的运动合成，获得过渡路径，完成插补。若下一段不是受限段，则依据公式(15)进行两段微线段的运动合成，从而获得过渡路径，完成插补。本例插补完成效果如图7所示。
[0190]
以上所述的实施例仅用于说明本发明的技术思想及特点，其目的在于使本领域内的技术人员能够理解本发明的内容并据以实施，不能仅以本实施例来限定本发明的专利范围，即凡本发明所揭示的精神所作的同等变化或修饰，仍落在本发明的专利范围内。