一种考虑输入量化和非线性死区的水下机器人无模型控制方法

1.本发明属于无人水下机器人运动控制技术领域，具体地，涉及一种考虑输入量化和非线性死区的水下机器人无模型控制方法。


背景技术：

2.水下无人航行器作为一类可以代替人完成水下任务的小型任务平台，其在海洋探索、环境观测以及侦察与监视等方面均体现了其独特的应用价值，轨迹跟踪控制作为一项auv 的核心技术，将在任务作业中产生优秀的性能。
3.保证快速精准的到达指定轨迹以及对其进行跟踪，水下航行器应该具备较好的航行稳定性以及抗干扰的能力，同时保证在有限的传输带宽中进行精确的控制信号的传输，执行机构的死区体现在对于数值较小的控制信号不够敏感，模型参数获取较为困难，即应该设计有效的运动控制律使得水下航行器在初始位置上进行轨迹跟踪来完成规定任务，并在短时间保证跟踪位置误差的全局一致渐近稳定。现有的方法解决模型参数问题采用的是神经网络以及模糊控制估计，此举会带来较大量的数据计算以及复杂计算，从而导致在估计不确定参数时耗时较多，无法精准控制水下航行器完成制定目标。


技术实现要素：

4.本发明提出了一种考虑输入量化和非线性死区的水下机器人无模型控制方法，为了加强水下无人航行器的鲁棒性能和忽略高度耦合动力学的影响，结合滑模控制的无模型控制能极大程度上减轻了对于很难获得的模型参数的依赖；考虑到减少执行机构和控制模块的数据传输的频率，磁滞量化器将产生分段量化控制信号，来保证其的有限精度以及有效地避免了抖振问题；自适应参数估计方法用来补偿死区非线性估计的误差，能够减少计算的复杂性和计算的次数，使得控制精度和效果大大提升。
5.本发明是通过以下方案实现的：
6.一种考虑输入量化和非线性死区的水下机器人无模型控制方法：
7.所述方法包括以下步骤：
8.步骤1：构建水下机器人的运动学和动力学模型，及无模型处理；
9.步骤2：引入磁滞量化器，简化考虑死区量化控制表达式，得到死区非线性的上界；
10.步骤3：设计控制器，得到死区非线性的上界的估计值；
11.步骤4：稳定性分析证明，证明最终误差收敛并保证一致终端有界稳定性。
12.进一步地，在步骤1中，
13.步骤1.1：所述水下机器人的运动学和动力学模型表达式为：
14.15.其中：η＝[x,y,z,φ,θ,ψ]
t
为在惯性坐标系下的位置和姿态的数值；
[0016]
v＝[u,v,w,p,q,r]
t
为在随体坐标系下的线速度和角速度的数值；
[0017]
正定矩阵m∈r6×6代表惯性矩阵；
[0018]
c(v)∈r6×6代表包含附加质量项的科里奥利向心力矩阵；
[0019]
d(v)∈r6×6代表流体阻尼矩阵；
[0020]
g∈r6×1代表重力和浮力作用在艇体所产生的恢复力和恢复力矩的向量；
[0021]
d为外界干扰所造成的扰动向量；
[0022]
τ为执行机构所产生的控制力和控制力矩；
[0023]
j(η)代表惯性坐标系与随体坐标系之间的坐标转换矩阵，
[0024]
j(η)定义为：
[0025][0026]
其中j1(η)和j2(η)定义分别如公式(3)(4)所示：
[0027][0028][0029]
m∈r6×6，c(v)∈r6×6，d(v)∈r6×6和g∈r6×1均保证一致有界和连续的向量，即 ||m||≤a1，||c(v)||≤a2||v||，||d(v)||≤a3+a4||v||，||g(η)||≤a5，其中a
i
(i＝1,2,...,5)均为未知正数；对于参考的运动轨迹η
d
∈r6，其一阶导数和二阶导数均保证有界和连续；
[0030]
步骤1.2：
[0031]
进行无模型处理，使用euler
‑
lagrange系统，将水下机器人的数学模型将转换成表达式公式(5)：
[0032][0033]
式中各项与步骤1.1中原运动学和动力学模型各项的关系表达式如公式(6)所示：
[0034][0035]
运用上述一致有界的约束，则有下列公式(7)的不等式：
[0036][0037]
进一步地，在步骤2中，
[0038]
步骤2.1：考虑死区的表达式定义为公式(8)所示：
[0039]
h(q(u))＝γ[q(u)+g(q(u))]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(8)
[0040]
其中，q(u)和g(q(u))分别为磁滞量化器和死区的非线性表达式；
[0041]
磁滞量化器q(u)的表达式如下所示；
[0042][0043]
步骤2.2：根据迟滞量化器的性质得知量化指令、量化前的连续指令和量化器参数之间存在以下关系；
[0044][0045]
步骤2.3：死区非线性g(q(u))为：
[0046][0047]
其中b
r
＞0和b
l
＜0均为未知的边界限制，则有g(q(u))＜χ，其中χ＞0为死区非线性的上界。
[0048]
进一步地，在步骤3中，
[0049]
步骤3.1：设计的滑模面定义如下：
[0050]
[0051]
步骤3.2：将公式(12)滑模面左乘转换后的惯性矩阵得：
[0052][0053]
步骤3.3：将公式(7)的不等式带入公式(12)得：
[0054][0055]
其中，α1，α2，α3，α4分别为：
[0056][0057]
步骤3.4：公式(14)、(15)整合得到公式(16)：
[0058][0059]
步骤3.5：使得误差收敛，则控制律公式为：
[0060][0061]
其中，λ1和λ2均为设定的正参数，正参数k2能够保证控制系统的渐近稳定性，k(t) 是为了补偿未知参数α
i
(i＝1,2,3,4,5)，k(t)定义为：
[0062]
[0063]
其中且代表自适应参数，自适应律定义为：
[0064][0065]
其中υ＞0,b
i
＞0和c
i
＞0；
[0066]
步骤3.6：估计值的自适应律定义如下：
[0067][0068]
其中ρ表示为正数，并被应用在lyapunov方程中。
[0069]
进一步地，在步骤4中，
[0070]
步骤4.1：选取lyapunov方程v1：
[0071][0072]
则公式(21)导数为：
[0073][0074]
步骤4.2：根据公式(7)中的不等式，得到下列各式：
[0075][0076]
步骤4.3：根据量化器的性质得到如下表达式：
[0077]
[0078]
将控制律代入表达式(24)，则有
[0079][0080]
步骤4.4：将公式(25)进行化简和合并同类相
[0081][0082]
步骤4.5：选取lyapunov方程v2：
[0083][0084]
对公式(27)进行求导，得到下述方程：
[0085][0086]
步骤4.6：选取lyapunov方程v3：
[0087][0088]
对公式(29)进行求导，得到下述方程：
[0089][0090]
步骤4.7：设定lyapunov最终方程：
[0091]
v＝v1+v2+v3ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(31)
[0092]
对公式(31)进行求导，得到下述方程：
[0093][0094]
其中，
[0095][0096][0097]
λ
max
(m(η))表示m(η)的最大特征值；
[0098]
最终误差将收敛至区域保证其一致终端有界稳定。
[0099]
本发明有益效果
[0100]
(1)本发明将海流扰动，模型不确定性以及死区非线性性质运用自适应控制来补偿误差，并引入磁滞量化器，能有效地避免通讯受限和抖振的问题。
[0101]
(2)相较于大多数无人水下航行器的轨迹跟踪控制方法，本发明方法无需知道水下无人航行器相关参数。采用本发明方法可使得水下无人航行器的控制系统在遭受到外界干扰和考虑输入死区的情况下，依旧保证优秀的跟踪性能。
附图说明
[0102]
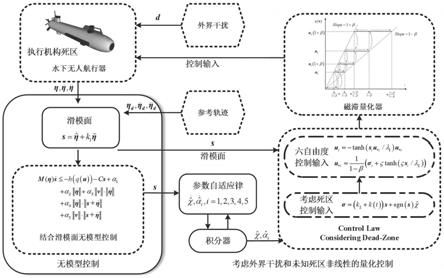
图1为本发明的水下机器人考虑输入量化和非线性死区无模型轨迹跟踪控制的原理图；
[0103]
图2为本发明的轨迹跟踪方法与其参考轨迹的仿真图，其中(a)x
‑
y
‑
z三维图，(b) x
‑
y平面图，(c)x
‑
z平面图，(d)y
‑
z平面图；
[0104]
图3(a)为本发明的无人航行器速度与预期的误差值，(b)为本发明的无人航行器实际位置和预期的误差值；
[0105]
图4(a)为本发明的无人航行器执行机构实际输出力(b)为本发明的无人航行器执行机构实际输出力矩；
[0106]
图5为本发明的无人航行器的参数α1,α2,α3,α4,α5,χ的估计值随时间变化图。
具体实施方式
[0107]
下面将结合本发明实施例中的附图对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例；基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0108]
结合图1至图5，
[0109]
一种考虑输入量化和非线性死区的水下机器人无模型控制方法：
[0110]
所述方法包括以下步骤：
[0111]
步骤1：构建水下机器人的运动学和动力学模型，及无模型处理；
[0112]
步骤2：引入磁滞量化器，简化考虑死区量化控制表达式，得到死区非线性的上界；
[0113]
步骤3：设计控制器，得到死区非线性的上界的估计值；
[0114]
步骤4：稳定性分析证明，证明最终误差收敛并保证一致终端有界稳定性。
[0115]
在步骤1中，
[0116]
步骤1.1：所述水下机器人的运动学和动力学模型表达式为：
[0117][0118]
其中：η＝[x,y,z,φ,θ,ψ]
t
为在惯性坐标系下的位置和姿态的数值；
[0119]
v＝[u,v,w,p,q,r]
t
为在随体坐标系下的线速度和角速度的数值；
[0120]
正定矩阵m∈r6×6代表惯性矩阵；
[0121]
c(v)∈r6×6代表包含附加质量项的科里奥利向心力矩阵；
[0122]
d(v)∈r6×6代表流体阻尼矩阵；
[0123]
g∈r6×1代表重力和浮力作用在艇体所产生的恢复力和恢复力矩的向量；
[0124]
d为外界干扰所造成的扰动向量；
[0125]
τ为执行机构所产生的控制力和控制力矩；
[0126]
j(η)代表惯性坐标系与随体坐标系之间的坐标转换矩阵，
[0127]
j(η)定义为：
[0128][0129]
其中j1(η)和j2(η)定义分别如公式(3)(4)所示：
[0130][0131][0132]
在运动学和动力学模型中，m∈r6×6，c(v)∈r6×6，d(v)∈r6×6和g∈r6×1各项均保证一致有界和连续的向量，即||m||≤a1，||c(v)||≤a2||v||，||d(v)||≤a3+a4||v||，||g(η)||≤a5，其中a
i
(i＝1,2,
…
,5)均为未知正数；对于参考的运动轨迹η
d
∈r6，其一阶导数和二阶导数均保证有界和连续；
[0133]
步骤1.2：
[0134]
在接下来的方法设计中，为了进行无模型运算，将使用euler
‑
lagrange系统，所以 auv的数学模型将转换成如下表达式：
[0135][0136]
式中各项与步骤1.1中原运动学和动力学模型各项的关系表达式如公式(6)所示：
[0137][0138]
运用上述一致有界的约束，则有下列公式(7)的不等式：
[0139][0140]
在步骤2中，
[0141]
步骤2.1：考虑死区的表达式定义为公式(8)所示：
[0142]
h(q(u))＝γ[q(u)+g(q(u))]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(8)
[0143]
其中，q(u)和g(q(u))分别为磁滞量化器和死区的非线性表达式；
[0144]
磁滞量化器q(u)的表达式如下所示；
[0145][0146]
步骤2.2：根据迟滞量化器的性质得知量化指令、量化前的连续指令和量化器参数之间存在以下关系；
[0147][0148]
在实际应用中，只有需要量化的状态信息才能传输给控制器，信号的量化取决于实际信号的传输带宽。否则，系统会增加功耗，使控制性能恶化，甚至造成系统不稳定。在这方面，合理的信号采样和量化设计对于利用有限的资源具有重要意义。而信号传输成功的
关键在于量化稳定。
[0149]
步骤2.3：死区非线性g(q(u))为：
[0150][0151]
其中b
r
＞0和b
l
＜0均为未知的边界限制，则有g(q(u))＜χ，其中χ＞0为死区非线性的上界。
[0152]
在步骤3中，
[0153]
步骤3.1：设计的滑模面定义如下：
[0154][0155]
滑模控制具有响应速度快、对参数变化和干扰不敏感等优点，具有较好的鲁棒性。然而，工程中经常出现离散开关引起的抖振现象，这是一个值得重视的问题。因此，在控制设计部分采用减小抖振的方法将会减弱滑模控制的负面影响。
[0156]
步骤3.2：将公式(12)滑模面左乘转换后的惯性矩阵得：
[0157][0158]
步骤3.3：将公式(7)的不等式带入公式(12)得：
[0159][0160]
为简化下面的推导和分析，将采用部分参数定义如下所示：其中，α1，α2，α3，α4分别为：
[0161][0162]
步骤3.4：公式(14)、(15)整合得到公式(16)：
[0163][0164]
步骤3.5：确保误差收敛至一个特定的区域，考虑到执行机构死区和水下航行器是六自由度，控制律设计为：
[0165][0166]
其中，λ1和λ2均为设定的正参数，正参数k2能够保证控制系统的渐近稳定性，k(t) 是为了补偿未知参数α
i
(i＝1,2,3,4,5)，k(t)定义为：
[0167][0168]
其中且代表自适应参数，自适应律定义为：
[0169][0170]
其中υ＞0,b
i
＞0和c
i
＞0；
[0171]
控制方案中的参数是缓解抖振的针对性措施，抖振可能会使参考轨迹产生不可消除的偏置。因此选择合适的参数值来平衡抖振和偏置是至关重要的。
[0172]
步骤3.6：估计值的自适应律定义如下：
[0173][0174]
其中ρ表示为正数，将会被应用在lyapunov方程中。
[0175]
5.根据权利要求1所述方法，其特征在于：在步骤4中，
[0176]
步骤4.1：选取lyapunov方程v1：
[0177][0178]
则公式(21)导数为：
[0179][0180]
步骤4.2：根据公式(7)中的不等式，得到下列各式：
[0181][0182]
步骤4.3：考虑到量化器的重要性质得到如下表达式：
[0183][0184]
将控制律代入表达式(24)，则有
[0185][0186]
步骤4.4：将公式(25)进行化简和合并同类相
[0187][0188]
步骤4.5：选取lyapunov方程v2：
[0189][0190]
对公式(27)进行求导，得到下述方程：
[0191][0192]
步骤4.6：选取lyapunov方程v3：
[0193][0194]
对公式(29)进行求导，得到下述方程：
[0195][0196]
步骤4.7：设定lyapunov最终方程：
[0197]
v＝v1+v2+v3ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(31)
[0198]
对公式(31)进行求导，得到下述方程：
[0199][0200]
其中，
[0201][0202][0203]
λ
max
(m(η))表示m(η)的最大特征值；
[0204]
最终误差将收敛至区域保证其一致终端有界稳定。
[0205]
经过上述推导过程证明，可以得到设计的水下航行器轨迹跟踪控制能够满足控制系统的稳定条件。给定系统的状态量初始值选为：x(0)＝0m，y(0)＝3m，z(0)＝0.5m，θ(0)＝0，φ(0)＝0，ψ(0)＝0，初始线速度均为0.1m/s，初始角速度均为0，参考轨迹的方程为：x
d
(t)＝5sin0.5t，y
d
(t)＝5cos0.5t，z
d
(t)＝0.05t+1，φ
d
(t)＝0rad，θ
d
(t)＝arctan(1/π)rad，ψ
d
(t)＝0.5rad。
[0206]
在给定干扰的情况下，其各方向的干扰力表达式分别为：
[0207]
τ
d1
＝
‑
1.5sin(0.6t)n
[0208]
τ
d2
＝
‑
sin(0.5t)n
[0209]
τ
d3
＝
‑
2sin(0.4t)
‑
5cos(0.2t)n
[0210]
τ
d4
＝
‑
1.5cos(0.2t)n
[0211]
τ
d5
＝
‑
sin(0.3t)
‑
3cos(0.3t)n
[0212]
τ
d6
＝
‑
2sin(0.1t)n
[0213]
经过仿真实验的验证，根据图2所示的效果而言，其跟踪效果较好，同时能够保证在短时间内达到所跟踪的轨迹曲线；根据图3所示，在运用了本发明提出的方法可以保证水下航行器在20秒内能够保证误差收敛至极小的值，此值作为可接纳区间能够保证其控制系统的稳定性能；根据图4所示，由于执行机构具有输出限额使得最大输出在最开始时为 1000n
·
m，随着跟踪时间增加，其控制力矩将会呈现周期性变化；根据图5所示，可以得知各项参数值的随时间的变化趋势，能够保证整个系统的稳定性能。
[0214]
以上对本发明所提出的一种考虑输入量化和非线性死区的水下机器人无模型控制方法，进行了详细介绍，对本发明的原理及实施方式进行了阐述，以上实施例的说明只是用于帮助理解本发明的方法及其核心思想；同时，对于本领域的一般技术人员，依据本发明的思想，在具体实施方式及应用范围上均会有改变之处，综上所述，本说明书内容不应理解为对本发明的限制。