一种基于健康状态数据的混合变量过程监测方法

1.本发明属于故障诊断领域，具体涉及一种基于健康状态数据的混合变量过程监测方法。


背景技术：

2.过程监测是工业系统安全、平稳运行的前提和保障。随着现代工业过程不断的大型化、集成化和复杂化，监测变量除了有连续变量以外还出现了二值变量。在仅能获得健康状态数据的情况下，传统监测方法仅仅基于连续变量进行，故障检测能力低。


技术实现要素：

3.针对同时包含连续变量和二值变量的混合变量系统，而且仅健康状态数据可获得的情况，本发明提出了一种基于健康状态数据的混合变量过程监测方法。该方法同时利用连续变量和二值变量信息，故障检测能力更强。
4.本发明的技术方案如下：
5.一种基于健康状态数据的混合变量过程监测方法，包括如下步骤：
6.步骤1：离线建模，具体包括如下步骤：
7.步骤1.1：采集健康状态训练数据集其中包含n个样本，为第i个采样并包含d个样本，i表示采样时间；x
i
共包含d
c
个连续特征和d
b
个二值特征；记x
j
为第j个变量；
8.步骤1.2：当x
j
为连续变量时，设其在健康状态下服从高斯分布
[0009][0010]
其中μ
j
和σ
j
分别为第j个变量在健康状态下的均值和标准差；
[0011]
步骤1.3：当x
j
为二值变量时，设其在健康状态下服从伯努利分布
[0012][0013]
其中η
j
为第j个变量在健康状态下的响应函数；
[0014]
步骤1.4：确定先验正常概率p(n)，取p(n)为置信水平即其中δ为显著水平；
[0015]
步骤1.5：对连续变量按照下式构造健康状态下的二值变量
[0016][0017]
然后所有关于权值的计算都用构造的二值变量代替原始的连续变量进行计算；
[0018]
步骤1.6：计算健康状态下的概率
[0019][0020]
其中为示性函数，当计算x
j
＝1的概率时否则
[0021]
步骤1.7：计算健康状态下的联合概率
[0022][0023]
其中
[0024]
步骤1.8：计算健康状态下的条件互信息
[0025][0026]
步骤1.9：如果x
j
和x
j
′
为连续变量，则按照下式进行修正
[0027][0028]
其中x
′
j
和x
′
j
′
分别为x
j
和x
j
′
根据步骤1.5构造的二值变量；
[0029]
步骤1.10：计算变量权值
[0030][0031]
步骤1.11：当x
j
为二值变量时，计算其在健康状态下的响应函数
[0032][0033]
步骤1.12：当x
j
为连续变量时，计算其在健康状态下的均值
[0034][0035]
步骤1.13：当x
j
为连续变量时，计算其在健康状态下的标准差
[0036][0037]
步骤1.14：计算样本x
i
的条件概率
[0038]
p(n|x
i
)＝p(n)p(x
i
|n)(12)
[0039]
其中j
c
为连续变量集的第j
c
个变量，j
b
为二值变量集的第j
b
个变量；
[0040]
步骤1.15：计算样本x
i
的函数f(x
i
)
[0041]
f(x
i
)＝lnp(n|x
i
)(13)
[0042]
步骤1.16：计算样本x
i
的统计量s
i
[0043]
s
i
＝f2(x
i
)(14)
[0044]
步骤1.17：通过核密度估计计算s＝[s1,
…
,s
i
,...s
n
]的控制限s
lim
；
[0045]
步骤2：在线检测，具体包括如下步骤：
[0046]
步骤2.1：当有新采样x
a
到来时，计算其条件概率
[0047]
p(n|x
a
)＝p(n)p(x
a
|n)(15)
[0048]
步骤2.2：计算样本x
a
的函数f(x
a
)
[0049]
f(x
a
)＝lnp(n|x
a
)(16)
[0050]
步骤2.3：计算样本x
a
的统计量s
a
[0051]
s
a
＝f2(x
a
)(17)
[0052]
步骤2.4：将统计量s
a
与控制限s
lim
进行比较，判断故障发生情况。
[0053]
优选地，故障发生情况的具体判断准则为：若新采样数据的统计量s
a
未超过控制限s
lim
，则认为正常，否则认为发生故障。
[0054]
本发明所带来的有益技术效果：
[0055]
针对同时包含连续变量和二值变量的混合变量系统，同时利用连续变量和二值变量信息进行过程监测，与传统的基于连续变量的方法相比，仅健康状态数据可获得的情况，故障检测能力更强。
附图说明
[0056]
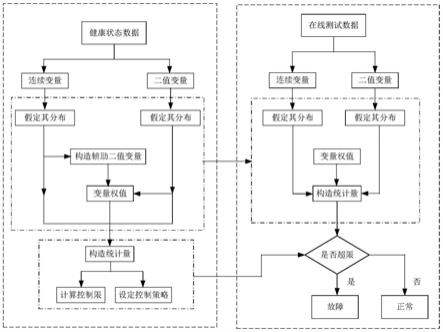
图1为本发明基于健康状态数据的混合变量过程监测方法的流程图；
[0057]
图2为本发明对比实验中pca的t2统计图；
[0058]
图3为本发明对比实验中pca的q统计图；
[0059]
图4为本发明对比实验中dpca的t2统计图；
[0060]
图5为本发明对比实验中dpca的q统计图；
[0061]
图6为本发明对比实验中ica的i2统计图；
[0062]
图7为本发明对比实验中ica的统计图；
[0063]
图8为本发明对比实验中ica的q统计图；
[0064]
图9为本发明对比实验中md的统计图；
[0065]
图10为本发明对比实验中hvm的统计图。
具体实施方式
[0066]
下面结合附图以及具体实施方式对本发明作进一步详细说明：
[0067]
如图1所示，一种基于健康状态数据的混合变量过程监测方法，包括如下步骤：
[0068]
步骤1：离线建模，具体包括如下步骤：
[0069]
步骤1.1：采集健康状态训练数据集其中包含n个样本，为第i个采样并包含d个样本，i表示采样时间；x
i
共包含d
c
个连续特征和d
b
个二值特征；记x
j
为第j个变量；
[0070]
步骤1.2：当x
j
为连续变量时，假设其在健康状态下服从高斯分布
[0071][0072]
其中μ
j
和σ
j
分别为第j个变量在健康状态下的均值和标准差；
[0073]
步骤1.3：当x
j
为二值变量时，假设其在健康状态下服从伯努利分布
[0074][0075]
其中η
j
为第j个变量在健康状态下的响应函数；
[0076]
步骤1.4：确定先验正常概率p(n)，通常取p(n)为置信水平即其中δ为显著水平；
[0077]
步骤1.5：对连续变量按照下式构造健康状态下的二值变量
[0078][0079]
然后所有关于权值的计算都用构造的二值变量代替原始的连续变量进行计算。
[0080]
步骤1.6：计算健康状态下的概率
[0081][0082]
其中为示性函数(当计算x
j
＝1的概率时否则)；
[0083]
步骤1.7：计算健康状态下的联合概率
[0084]
[0085]
其中
[0086]
步骤1.8：计算健康状态下的条件互信息
[0087][0088]
步骤1.9：如果x
j
和x
j
′
为连续变量，则按照下式进行修正
[0089][0090]
其中x
′
j
和x
′
j
′
分别为x
j
和x
j
′
根据步骤1.5构造的二值变量；
[0091]
步骤1.10：计算变量权值
[0092][0093]
步骤1.11：当x
j
为二值变量时，计算其在健康状态下的响应函数
[0094][0095]
步骤1.12：当x
j
为连续变量时，计算其在健康状态下的均值
[0096][0097]
步骤1.13：当x
j
为连续变量时，计算其在健康状态下的标准差
[0098][0099]
步骤1.14：计算样本x
i
的条件概率
[0100]
p(n|x
i
)＝p(n)p(x
i
|n)(12)
[0101]
其中j
c
为连续变量集的第j
c
个变量，j
b
为二值变量集的第j
b
个变量；
[0102]
步骤1.15：计算样本x
i
的函数f(x
i
)
[0103]
f(x
i
)＝lnp(n|x
i
)(13)
[0104]
步骤1.16：计算样本x
i
的统计量s
i
[0105]
s
i
＝f2(x
i
)(14)
[0106]
步骤1.17：通过核密度估计计算s＝[s1,...,s
i
,...s
n
]的控制限s
lim
。
[0107]
步骤2：在线检测，具体包括如下步骤：
[0108]
步骤2.1：当有新采样x
a
到来时，计算其条件概率
[0109]
p(n|x
a
)＝p(n)p(x
a
|n)(15)
[0110]
步骤2.2：计算样本x
a
的函数f(x
a
)
[0111]
f(x
a
)＝lnp(n|x
a
)
(16)
[0112]
步骤2.3：计算样本x
a
的统计量s
a
[0113]
s
a
＝f2(x
a
)(17)
[0114]
步骤2.4：将统计量s
a
与控制限s
lim
进行比较，判断故障发生情况；若新采样数据的统计量s
a
未超过控制限s
lim
，则认为正常，否则认为发生故障。
[0115]
为了充分证明本发明的可行性和优越性，进行了仿真研究。仿真实例包含10个变量，其中5个连续变量x1,x2,x3,x4,x5，5个二值变量x6,x7,x8,x9,x
10
。连续变量在正常和故障条件下服从高斯分布，其参数如表1所示。二值变量在正常和故障条件下的数值和调整比例如表2所示。正常条件下产生健康状态数据4000个数据用于训练模型，然后产生4000数据用于测试，其中前2000个为正常数据，后2000个为故障数据。
[0116]
表1连续变量分布
[0117]
变量正常故障x1n(1.50,0.762)n(0.55,0.552)x2n(3.00,0.682)n(2.55,1.012)x3n(1.70,0.852)n(2.20,1.002)x4n(0.80,1.012)n(1.45,0.912)x5n(0.89,0.642)n(1.30,0.552)
[0118]
表2二值变量参数
[0119][0120]
本发明选取了主成分分析(pca)、动态主成分分析(dpca)、独立主元分析(ica)、马氏距离(md)四个方法与本发明所提混合变量监测(hvm)方法进行了对比实验，各方法的统计量结果如图2
‑
10所示。其中，图2为pca的t2统计图，图3为pca的q统计图，图4为dpca的t2统计图，图5为dpca的q统计图，图6为ica的i2统计图，图7为ica的i
e2
统计图，图8为ica的q统计图，图9为md的统计图，图10为本发明方法hvm的统计图。pca和dpca的累计贡献率为0.8，dpca的时间叠加为2，ica的独立主元数为3。
[0121]
五个方法均独立重复进行100次实验，各方法的故障误报率(far)和故障检测率(fdr)均值如表3所示。可以看出，本发明所提混合变量监测(hvm)方法在保证故障检测率最高的前提下，误报率仍保持在较低水平线上。
[0122]
表3实验方式及检测结果对比
[0123][0124]
当然，上述说明并非是对本发明的限制，本发明也并不仅限于上述举例，本技术领域的技术人员在本发明的实质范围内所做出的变化、改型、添加或替换，也应属于本发明的保护范围。