一种输入受限的机械系统保性能自调节控制方法

1.本发明属于自动控制技术领域。


背景技术：

2.对于存在外部干扰的一般机械系统，其高性能控制问题有着广泛研究兴趣与应用价值。在诸多研究方法中，预设性能控制方法通过在lyapunov函数中引入非线性映射，使得当状态趋近给定约束时，lyapunov函数将趋向于无穷。因此，当能保证lyapunov函数有界时，即可实现对状态的约束。预设性能控制方法的优势在于将复杂的约束问题转化为常规的lyapunov函数稳定问题，为用户在lyapunov函数中嵌入性能需求，提供了便利。
3.然而，实际的机械系统能够提供的控制能量必然是有限的，具有输入饱和特性，也意味着能够实现的性能需求是有限。这就导致用户设立的性能需求存在无法实现的情况，强行引入预设性能控制方法，存在控制失效甚至系统失控的可能，这一情况极大的制约了预设性能方法在实际对象中的应用。


技术实现要素：

4.发明目的：为了解决上述现有技术存在的问题，本发明提供了一种输入受限的机械系统保性能自调节控制方法。
5.技术方案：本发明提供了一种输入受限的机械系统保性能自调节控制方法，包括如下步骤：
6.步骤1：针对具有一般性的机械系统建立机械系统方程；
7.步骤2：计算机械系统的跟踪误差，在客户预设的跟踪误差性能约束中引入自调节信号，得到自调节性能约束，采用保性能控制方法对跟踪误差进行转换，使得跟踪误差满足自调节性能约束，并得到误差转换后的变量；
8.步骤3；建立有限时间的自调节辅助系统，该自调节辅助系统用于生成自调节信号；
9.步骤4：根据步骤3自调节辅助系统生成的自调节信号和步骤2误差转换后的变量，建立保性能有限时间的自调节控制器，当机械系统的输入存在不饱和的情况下，该自调节控制器在有限时间内将机械系统的跟踪误差恢复至满足自调节性能约束的要求。
10.进一步的，所述步骤1中的系统方程为：
[0011][0012]
其中，xc和xq均为n维的向量，均表示系统中能够被传感器测量到的状态；为xc的一阶导数，为xq的一阶导数；f(xc，xq)＝-m
inv
(xc)(c(xc，xq)xq+g(xc))，m(xc)为惯性矩阵，inv为逆变换，c(xc，xq)为科氏效应与离心效应矩阵，g(xc)是关于系统势能的函数，g(xc)＝m
inv
(xc)，τc为系统的输入力矩，τc＝[τ
c，1
，...，τ
c，i
，...，τ
c，n
]
t
，t为矩阵转置，τ
c，i
为τc中的第i个元素，i＝1，2，...，n；τd为有界的外部干扰力矩。
[0013]
进一步的，所述步骤2中的自调节性能约束为：
[0014]-λ
l，0，i-λ
l，c，i
＜e
c，i
＜λ
u，0，i
+λ
u，c，i
[0015]
其中，e
c，i
为跟踪误差向量ec中第i个元素，ec＝[e
c，1
，...，e
c，i
，...，e
c，n
]
t
，λ
u，0，i
为预设的第一恒正的时变向量λ
u，0
中第i个元素，λ
u，0
＝[λ
u，0，1
，...，λ
u，0，i
，...，λ
u，0，n
]
t
；λ
u，c，i
为第一自调节信号λ
u，c
中第i个元素，λ
u，c
＝[λ
u，c，1
，...，λ
u，c，i
，...，λ
u，c，n
]
t
；λ
l，0，i
为预设的第二恒正的时变向量λ
l，0
中第i个元素，λ
l，0
＝[λ
l，0，1
，...，λ
l，0，i
，...，λ
l，0，n
]
t
；λ
l，c，i
为第二自调节信号λ
l，c
中第i个元素，λ
l，c
＝[λ
l，c，1
，...，λ
l，c，i
，...，λ
l，c，n
]
t
；
[0016]
步骤2中误差转换后的变量为：
[0017][0018]
其中tc(
·
)为误差转换函数，且tc(
·
)和z
c，i
满足如下条件：
[0019]
条件1：条件1：为无穷阶可微函数；
[0020]
条件2：-1＜tc(z
c，i
)＜1，-∞＜z
c，i
＜∞；
[0021]
条件3：
[0022]
进一步的，所述步骤3中的自调节辅助系统为：
[0023][0024]
其中，k∈{u，l}，为λ
k，c
的一阶导数，zc＝[z
c，1
，...，z
c，i
，...，z
c，n
]
t
，υc与υq均为待设计的负定对角矩阵，α和p均为调节参数，且0＜α＜1，p＞0；λ
k，q
为自调节辅助系统的状态，为λ
k，q
的一阶导数；与均为幂形式的阻尼项；均为幂形式的阻尼项；(
·
)-＝(
·
)-(
·
)
+
，(
·
)
+
表示取矩阵或向量中的正元素并对负元素赋零，τr为保性能有限时间的自调节控制器生成的期望力矩，为标称的输入力矩。
[0025]
进一步的，所述步骤4中的保性能有限时间的自调节控制器为：
[0026][0027]
其中，kq为常数矩阵，ρq为调节参数，且ρq＞0；为虚拟控制律，χf为设计的滤波器的输出，滤波器的表达式为：ρf为参数，且ρf＞0；为χf的一阶导数；为滤波器的输入，的表达式为：
[0028][0029]
xr为预设的连续可微的参考信号，为xr的一阶导数；ρc为调节参数，且ρc＞0；kc为正定的增益矩阵。
[0030]
有益效果：本发明能够在输入饱和后，由辅助系统生成自调节信号，适当放宽性能约束，并在输入不饱和后的有限时间内恢复预设性能，从而实现对输入约束与输出约束的协调，最终避免性能函数过激导致的奇异性问题，提高了保性能控制方法的可靠性。
附图说明
[0031]
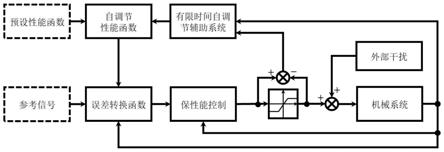
图1为本发明的闭环系统框图。
具体实施方式
[0032]
构成本发明的一部分的附图用来提供对本发明的进一步理解，本发明的示意性实施例及其说明用于解释本发明，并不构成对本发明的不当限定。
[0033]
如图1所示，本实施例提供一种输入受限的机械系统保性能自调节控制方法，该方法具体为：
[0034]
步骤一：明确系统描述与性能需求
[0035]
为便于发明描述，定义如下运算符号：运算符(
·
)
t
表示对矩阵或向量转置；运算符(
·
)
+
表示取矩阵或向量中的正元素并对负元素赋零，并有(
·
)-＝(
·
)-(
·
)
+
；表征实数集，数集，为n维欧几里得空间，为n维欧几里得空间，对于两个矩阵或向量a＝[a
ij
]与b＝[b
ij
]，表示其中符号max{a，b}＝[max{a
ij
，b
ij
}]；a
+
＝max{a，0}；a-＝a
+-a；|a|＝a
+
+a-；对于实对称矩阵a，a＜0与a＞0分别表示矩阵a是负定与正定的；λ
max
(a)与λ
min
(a)分别表示矩阵a的最大与最小特征值；对于可逆矩阵a，a
inv
表示a的逆矩阵；||
·
||
∞
表示范数；λ
min
(
·
)表示取矩阵的最小特征根。
[0036]
本发明考虑具有一般性的机械系统，并描述为如下欧拉-拉格朗日方程：
[0037][0038]
其中，f(xc，xq)＝-m
inv
(xc)(c(xc，xq)xq+g(xc))，和和均表示系统中能够被传感器测量到的状态，为系统的实际力(矩)输入，为有界的外部干扰力(矩)，为惯性矩阵，且有其中，为常数矩阵，为科氏效应与离心效应矩阵，g(xc)是关于系统势能的函数。此外，受制于作动器的效能，输入力(矩)τc＝[τ
c，1
，...，τ
c，n
]
t
存在饱和非线性，并与控制器生成的期望力(矩)τr＝[τ
r，1
，...，τ
r，n
]
t
之间存在如下映射关系：
[0039][0040]
其中，τ
max
＝[τ
max，1
，...，τ
max，n
]
t
和τ
min
＝[τ
min，1
，...，τ
min，n
]
t
为未知的常值向量表征执行器的饱和非线性。
[0041]
系统的控制设计目标如下：设计状态反馈控制律，使得状态xc有界跟踪二阶连续可微的参考信号并且在输入不饱和的情况下保证跟踪误差矩阵ec＝[e
c，1
，...，ec，i
，...，e
c，n
]
t
＝x
c-xr满足如下预设性能约束：
[0042]-λ
l，0，i
(t)＜e
c，i
(t)＜λ
u，0，i
(t)，i＝1，...，n
ꢀꢀ
(3)
[0043]
其中，e
c，i
为跟踪误差矩阵ec中第i个元素，和为预设的恒正的时变向量表征用户给定的预设性能。λ
l，0，i
为λ
l，0
中第i个元素，λ
u，0，i
为λ
u，0
中第i个元素。
[0044]
步骤二：构造自调节性能函数及误差转换
[0045]
鉴于考虑的机械系统存在输入饱和非线性，当饱和后发生后，即τc(τr)≠τr，必然存在约束失效的可能。因此，本发明在原先的预设性能约束中引入自调节信号，衍生出的自调节性能约束可写成如下形式：
[0046]-λ
l，0，i-λ
l，c，i
＜e
c，i
＜λ
u，0，i
+λ
u，c，i
，i＝1，...，n
ꢀꢀꢀ
(4)
[0047]
其中，和为自调节信号，λ
l，c，i
为λ
l，c
中第i个元素，λ
u，c，i
为λ
u，c
中第i个元素，将由后续的辅助系统生成。为了保证上述自调节性能约束，采用如常规保性能控制方法进行误差变换，
[0048]ec，i
＝0.5(λ
u，0，i
+λ
u，c，i
+λ
l，0，i
+λ
l，c，i
)tc(z
c，i
)+0.5(λ
u，0，i
+λ
u，c，i-λ
l，0，i-λ
l，c，i
)
ꢀꢀ
(5)
[0049]
也既：
[0050][0051]
其中tc(
·
)为误差转换函数，且tc(
·
)和z
c，i
满足如下条件：
[0052]
条件一：条件一：为无穷阶可微函数；
[0053]
条件二：-1＜tc(z
c，i
)＜1，-∞＜z
c，i
＜∞；
[0054]
条件三：
[0055]
为方便后续表述，令zc＝[z
c，1
，...，z
c，n
]
t
，定义如下矩阵：
[0056][0057]
步骤三：设计有限时间自调节辅助系统
[0058]
鉴于控制目标中已明确指出，自调节信号λ
u，c
和λ
l，c
对预设的性能约束仅有放宽作用，所以辅助系统的设计需要保证信号始终非负。同时，考虑到当输入不再饱和后要在有限时间内恢复预设性能约束，本发明采用有限时间收敛方法进行设计。此外，由于执行器的饱和非线性是未知的，因此另外引入如下的饱和非线性函数：
[0059][0060]
其中，为系统标称的输入力(矩)，和为已知的常值向量，显然，有界。
[0061]
令k∈{u，l}、j∈{q，c}，则自调节辅助系统设计如下：
[0062][0063]
其中，k∈{u，l}，为λ
k，c
的一阶导数，zc＝[z
c，1
，...，z
c，i
，...，z
c，n
]
t
，υc与υq为待设计的负定对角矩阵，j∈{q，c}，α和p均为调节参数，且0＜α＜1，p＞0；λ
k，q
为辅助系统状态向量，λ
k，q
＝[λ
k，q，1
，...，λ
k，q，i
，...，λ
k，q，n
]
t
，λ
k，q，i
为λ
l，q
中第i个元素，为λ
k，q
的一阶导数；的一阶导数；与为幂形式的阻尼项，sign(
·
)为符号函数；)为符号函数；保性能有限时间的自调节控制器生成的期望力矩，为标称的输入力矩。
[0064]
结论1：针对存在输入受限的机械系统1，设计自调节辅助系统如式8。对于任意给定的正常数向量当系统的标称力(矩)输入与控制器生成的期望力(矩)τr满足条件如下：
[0065][0066]
则存在常数向量和使得辅助系统的状态始终在如下紧集中：
[0067][0068]
同时，当输入不再饱和后，即时，辅助系统状态将在有限时间内收敛；
[0069]
证明：1)非负性：考虑辅助系统8，其状态λ
u，q
和λ
l，q
的动态可以整理成如下形式：
[0070][0071]
其中，为关于λ
k，q
的非线性对角矩阵，且有鉴于设计条件λ
k，q
≥0，λ
k，q
(0)＝0与为metzler矩阵，由正系统理论可得为metzler矩阵，由正系统理论可得进一步考虑状态λ
u，c
和λ
l，c
的动态，由于ωu和ω
l
是对角矩阵，则ωuυc和ω
l
υc是也metzler(对角)矩阵，与上述过程相似，可得
[0072]
2)有界性：考虑式11，状态向量λ
u，q
和λ
l，q
中各个元素的动态可以写成如下形式：
[0073][0074]
其中，由于υq＝diag{υ
q，1
，...，υ
q，i
，...，υ
q，n
}为负定对角矩阵，υ
q，i
为其第i个对角元素，则当λ
k，q，i
≥-f
k，q，i
/υ
q，i
时有进而可得λ
k，q，i
≤-f
k，q，i
/υ
q，i
。再由条件9、λ
k，q，i
≥0以及可知则有进一步考虑λ
u，c
和λ
l，c
，其各个元素的动态满足：
[0075][0076]
与上述分析过程相似，由和λ
k，c，i
≥0，且υc＝diag{υ
c，1
，...，υ
c，i
，...，
υ
c，n
}为负定对角矩阵，υ
c，i
为其第i个对角元素，可知：当λ
k，c，i
≥-λ
k，q，i
/υ
c，i
时，有进而可得λ
k，c，i
≤-||λ
k，q，i
||∞/υ
q，i
。再由可得综上可得，辅助系统的状态始终在紧集中。
[0077]
3)有限时间收敛特性：当存在时刻t
f，0
＜∞使得有λ
u，τ
＝0和λ
l，τ
＝0。选取lyapunov函数为其导数满足：
[0078][0079]
则根据有限时间收敛理论，存在有限时刻t
f，0
≤t
f，1
＜∞，辅助系统状态λ
u，q
和λ
l，q
收敛。进而对于任意t≥t
f，1
，有λ
u，q
(t)＝λ
l，q
(t)＝0。进一步选取lyapunov函数为(t)＝0。进一步选取lyapunov函数为其导数满足：
[0080][0081]
则存在有限时刻t
f，1
≤t
f，2
＜∞，辅助系统状态λ
u，c
和λ
l，c
收敛至零。
[0082]
步骤四：设计保性能有限时间自调节控制
[0083]
基于上述自调节性能函数与自调节辅助系统，可设计控制律。首先针对转换后的变量zc＝[z
c，1
，...，z
c，n
]
t
，考虑机械系统模型与误差转换过程，其动态可以归纳成如下形式：
[0084][0085]
依照动态面控制方法，进一步定义误差其中，为需要设计的虚拟控制律。考虑辅助系统8，则有：
[0086][0087]
进而可有设计虚拟控制律如下：
[0088][0089]
其中，是滤波器的输出，滤波器的表达式为：
[0090][0091]
式中，ρf＞0为设计参数，为滤波器输入。通过引入参考信号xr的微分信号设计正定增益矩阵kc与调节参数ρc＞0，可给定滤波器输入如下：
[0092][0093]
通过定义滤波器估计误差将虚拟控制律13代入12可得
[0094][0095]
考虑机械系统1与辅助系统6，误差zq的动态可归纳如下：
[0096][0097]
进而可设计控制律如下：
[0098][0099]
其中，kq是预设的正定常数矩阵，ρq＞0也是可以进行调节的参数。
[0100]
定义向量m＝col{λ
u，c
，λ
l，c
，λ
u，q
，λ
l，q
}和y＝col{y0，τd}分别表示闭环系统所有的误差变量、辅助系统状态和外部输入。对于任意给定的常数和常数向量集合集合和都是紧集。相应地，也是紧集。而在紧集内，滤波器误差变量的导数可以写成：
[0101][0102]
其中，
[0103][0104]
表征滤波器输入的导数。鉴于函数δ
χ
(
·
)的连续特性，存在常数δ
δ
＞0在紧集中有如下特性：
[0105][0106]
至此，可给出闭环系统稳定性结论。为方便描述，令
[0107][0108]
结论2：针对输入受限的机械系统1，设立性能约束如式4，构建自调节辅助系统如式8，基于虚拟控制律13与滤波器14设计实际控制律17。任意给定的对于所有满足不等式当增益矩阵υc、υq、kc、kq，调节向量设计参数α、p、ρc、ρq、ρf满足如下条件：
[0109][0110][0111]
则闭环系统有界且跟踪误差始终满足约束4。此外，当存在时刻t
f，0
＜∞使得＜∞使得则在有限时间后，跟踪误差始终满足约束3。
[0112]
证明：选取lyapunov函数考虑15、16和18，则的导数满足如下形式：
[0113][0114]
代入式12与15，并考虑不等式18，可得：
[0115][0116][0117]
根据参数设计条件20与结论1，可知进而由参数设计条件21可得：当时，有则为不变集，即也为不变集。再由初始条件可得根据误差转换函数tc(
·
)的特性可知，跟踪误差始终满足约束4。对于任意的t≥t
f，0
，由结论1可知：在有限时间后，辅助系统状态将收敛至零，进而约束4与3等价。
[0118]
即跟踪误差满足预设性能约束另外需要说明的是，在上述具体实施方式中所描述的各个具体技术特征，在不矛盾的情况下，可以通过任何合适的方式进行组合。为了避免不必要的重复，本发明对各种可能的组合方式不再另行说明。