一种四旋翼无人机栖停机动轨迹优化方法

1.本发明属于无人机技术领域，具体涉及一种四旋翼无人机栖停机动轨迹优化方法。


背景技术：

2.微小型四旋翼无人机(micro quadrotor unmanned aerial vehicle，简称mquav)是当下的研究热点，在军事、民用等领域获得广泛应用。军事领域中，mquav装备于班组或单兵，用于战场侦查监视或者打击。民用领域中，mquav可以承担区域监控、数据采集、航空拍摄等任务。mquav以其低成本、轻小便携、强机动性等优势获得广泛关注，但无人机尺度减小伴随着储能空间急剧减缩，引发了续航时间缩短、使用效能恶化的严重问题。因此，提升mquav续航时间成为当下的一个亟待解决的热点问题。
3.垂面栖停策略是当前解决续航问题的一个有效手段，无人机垂面栖停过程如图1所示。栖停策略的灵感来源于鸟类栖落行为，是通过在无人机上加装模仿动物肢体的栖附装置，赋予无人机在线缆或者建筑物壁面栖附的能力。无人机栖附时仅借助外部作用力克服重力，无需驱动螺旋桨产生推力，因此，可以达到降低能耗、延长有效任务时间的目的。
4.随着栖停机动应用范围的日益广泛，与之相关的轨迹规划问题也就受到越来越广泛的关注。由于栖停机动过程的约束特征以及四旋翼无人机的欠驱动、强耦合特性，如何规划四旋翼无人机栖停机动轨迹成为本领域技术人员需要解决的重要技术问题。
5.cn113342056a提供了无人机智能控制技术领域的一种基于改进a星算法的无人机轨迹规划方法，在地图上设定一起始点以及一目标点，基于所述起始点以及目标点进行随机采样得到采样点利用a星算法以及所述节点距离矩阵进行最短路径搜索，完成无人机轨迹规划。cn106774421b公开了一种无人机轨迹规划系统，包括：无人机模块和云平台模块，其中，无人机模块用于采集当前无人机的飞行轨迹信息，并将该飞行轨迹信息上传至云平台模块；云平台模块用于对接收的飞行轨迹信息进行分析，并将对应的最优轨迹规划信息反馈给无人机模块所对应的无人机。cn110308699a公开了一种轨迹规划方法，该方法首先在笛卡儿空间中利用ph曲线平滑竖直运动与水平运动间的直角过渡部分，确定运动轨迹；接着利用多项式运动规律对轨迹的1维曲线位移进行规划，确定运动轨迹插补点的位置；最后以最小化拾放操作周期为目标优化ph曲线参数，并经过推导证明该优化方法能得到ph曲线下最小的曲率差。
6.现有技术能够根据运动路径开展前端的路径生成(cn113342056a)以及后端的轨迹优化(cn110308699a)，技术核心在于生成满足避障与轨迹光滑连续的运动轨迹。但是，对于栖停问题而言，所生成的轨迹不仅要满足动力学约束，还需要满足过程约束以及末端的速度、角度等约束，因而，该问题不在是单纯的路径规划问题，而应是混合约束条件下的轨迹规划问题。因此，在本发明中提出，采用罚函数方法结合数值优化构建垂面栖停的轨迹规划方法。


技术实现要素：

7.要解决的技术问题：
8.为了避免现有技术的不足之处，本发明提出一种四旋翼无人机栖停机动轨迹优化方法，用以解决四旋翼无人机垂面栖停运动轨迹规划问题。
9.本发明的技术方案是：一种四旋翼无人机栖停机动轨迹优化方法，其特征在于具体步骤如下：
10.步骤一：四旋翼无人机动力学建模；
11.坐标系选定：四旋翼无人机建模所需的坐标系，分别是地面坐标系ogxgygzg和机体坐标系obxbybzb；两坐标系的相对关系由滚转角φ、俯仰角θ和偏航角ψ三个角度来描述；
12.建立动力学方程，根据刚体运动学方程和动力学方程建立四旋翼无人机的纵向运动的动力学方程：
[0013][0014][0015][0016]
其中，f
x
为合外力在地面坐标系xg轴的分量，fz为合外力在地面坐标系zg轴的分量，m为无人机合力矩矢量在地面坐标系yg轴的分量；i为螺旋桨计数序号为，i＝1，2，3，4；fi为螺旋桨i的推力，mi为螺旋桨i的扭矩；u为无人机质心速度矢量在地面坐标系xg轴的分量，w为无人机质心速度矢量在地面坐标系zg轴的分量，q为无人机角速度矢量在地面坐标系yg分量；i为四旋翼无人机关于机体坐标系yb轴的转动惯量，m为无人机的质量；
[0017]
步骤二：生成开环运动轨迹；
[0018]
2.1.基于时间的运动轨迹求解；
[0019]
通过沿时间积分，获得无人机的位移与俯仰角随时间变化曲线，具体表达式为：
[0020][0021][0022][0023][0024][0025][0026]
式中，u0为t＝0时刻的u值，w0为为t＝0时刻的w值，q0为为t＝0时刻的q值。x0、z0分别为t＝0时刻的坐标值，θ0分别为t＝0时刻的俯仰角；
[0027]
2.2.基于距离的运动轨迹求解；
[0028]
根据当前时刻的坐标位置，采用插值方法求解当前时刻的推力，具体步骤如下：
[0029]
2.2.1问题设定：给定轨迹优化的起始位置、目标位置，确定运动约束；
[0030]
2.2.2推力设定：在给定飞行距离内进行划分，设定采样点数n+1，将轨迹均匀的划
分为n段，采用随机取样方法设定推力序列{f1(xj),f2(xj),f3(xj),f4(xj)}，j为采样点序号且j＝1～n+1，采用样条方法生成相对于距离坐标的推力曲线；
[0031]
2.2.3轨迹生成：采用时间推进方法求解飞行轨迹，当前时刻的推力由当前时刻对应的位置坐标在推力序列{f1(xj),f2(xj),f3(xj),f4(xj)}插值而来；
[0032]
2.2.4截止条件：当求解轨迹的水平坐标与目标点水平坐标一致时，轨迹求解终止；
[0033]
步骤三：混合约束条件下的轨迹优化；
[0034]
3.1.建立约束；
[0035]
四旋翼无人机在垂面栖停运动过程需要满足运动过程中最大需要推力小于电机最大推力，且着陆时满足步骤二确定的运动约束，具体表述如下：
[0036]
3.1.1动力约束：轨迹优化过程中，任意时刻的推力输出均小于单轴最大推力f
max
；
[0037]
3.1.2俯仰角约束：无人机在与栖停表面接触时刻，四旋翼无人机的俯仰角为θ
des
，确保无人机将其栖停装置朝向栖停表面；
[0038]
3.1.3速度约束：无人机在与栖停表面接触时刻，四旋翼无人机栖停表面速度u
des
范围为u
min
≤u
des
≤u
max
，法向速范围为w
min
≤w
des
≤w
max
；
[0039]
3.1.4位置约束：无人机在与栖停表面接触时刻，四旋翼无人机降落位置zf与目标位置z
des
的高度误差不超过某一数值，即|z
f-z
des
|≤ε，ε为容许误差；
[0040]
3.2.构造罚函数，包括性能函数、目标约束函数以及动力约束函数，表达式如下：
[0041]
cost＝j1+j2+j3[0042]
式中，j1为性能函数，j2为目标约束，j3为动力约束，各约束表达式如下：
[0043]
j1＝∑(t
·
v)
·
δt
[0044]
j2＝(u
f-u
des
)2+(w
f-w
des
)2+(θ
f-θ
des
)2[0045]
j3＝∑max{fi(t)-f
max
,0}
[0046]
3.3.构建优化求解器；
[0047]
基于步骤二中建立的基于距离的推力序列{f1(xj),f2(xj),f3(xj),f4(xj)}j＝1～n+1，通过罚函数结合数值优化算法来获得运动约束与动力学约束的可行轨迹；轨迹优化流程步骤如下：
[0048]
3.3.1初值设定：采用随机采样法生产初始推力时间序列的初始样本，该推力序列以距离为参考，记为{f1(xj),f2(xj),f3(xj),f4(xj)},j＝1～n+1，内部插值采用样条方法；
[0049]
3.3.2基于步骤二的运动轨迹生成方法解算运动轨迹，并计算罚函数；
[0050]
3.3.3采用数值优化算法对设计变量{f1(xj),f2(xj),f3(xj),f4(xj)},j＝1～n+1进行搜索并更新设计变量；
[0051]
3.3.4当罚函数数值小于阈值时，结束优化，否则，重复进行步骤3.3.2和步骤3.3.3。
[0052]
本发明的进一步技术方案是：所述步骤一中，地面坐标系是固定于地球的惯性坐标系，机体坐标系则是固定于无人机的坐标系，坐标系中心ob位于无人机质心，xb位于无人机对称面内指向前，zb位于无人机对称面内指向上，yb的确定满足右手坐标系。
[0053]
本发明的进一步技术方案是：所述步骤二2.2.1中，运动约束包括等式约束与不等式约束。
[0054]
本发明的进一步技术方案是：所述步骤二2.2.1中，运动约束包括位置、速度、姿态角、角速度。
[0055]
本发明的进一步技术方案是：所述步骤三3.1.3中，u
des
和w
des
的取值范围取决于步骤3.1.2中栖停装置的速度包线。
[0056]
本发明的进一步技术方案是：所述步骤三3.3.3中，数值优化算法采用遗传优化算法。
[0057]
本发明的进一步技术方案是：所述步骤三3.3.4中，阈值设定的原则是：
[0058]
设当前共计进行i次优化迭代，则产生i个优化设计结果；读取当前优化结果opti与上一次优化结果opt
i-1
，若|opt
i-opt
i-1
|/|opt
i-1
|＜δ,则认为优化过程收敛并结束优化过程；δ是人为设定的收敛误差，通常为一个量级为1％或1
‰
的数值。
[0059]
有益效果
[0060]
本发明的有益效果在于：本发明提供一种四旋翼无人机栖停机动轨迹优化方法。首先，该方法以动力学模型为基础，兼顾无人机机动能力约束，是动力学可行的飞行轨迹。其次，该方法将等式约束与不等式约束均纳入罚函数，通过对罚函数求最小值的方式将含约束优化问题转化为无约束最小值问题。相比于现有的“cn113342056a”等专利提出的前端路径规划+后端轨迹光顺的方法，本发明提出的轨迹优化方法在开环运动轨迹基础上进行寻优，能够直接获得最优飞行轨迹，避免了后端轨迹广顺所需的计算时间与计算资源，算法更加直接与简单。从数值计算角度来看，罚函数方法简化了对约束处理所需的计算量，并且，罚函数结合数字优化方法有助于实现在设计变量全局进行寻优，因而，本方法的数值计算工作量更小，计算效率更高且能达到较好的优化设计效果。
[0061]
本发明提供一种四旋翼无人机栖停机动轨迹优化方法，该方法具有动力学的可行性、数值计算工作量减小、规划效率高的优点。
附图说明
[0062]
图1为四旋翼无人机垂面栖停示意图；
[0063]
图2为四旋翼无人机开环运动轨迹求解流程图；
[0064]
图3为本发明实施例中四旋翼无人机轨迹优化流程图；
[0065]
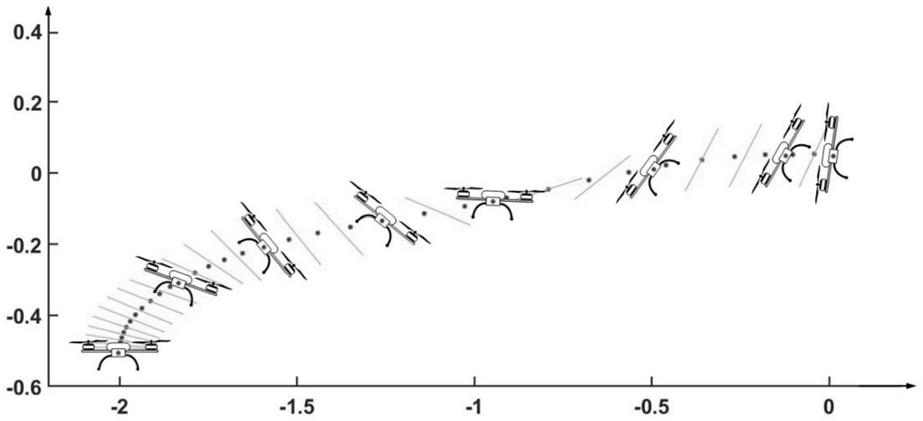
图4为本发明实施例中四旋翼无人机运动轨迹示意图；
[0066]
图5为本发明实施例中四旋翼无人机的轨迹变化曲线图；(a)为四旋翼无人机的高度随位置变化曲线；(b)为四旋翼无人机的俯仰角随位置变化曲线；(c)为四旋翼无人机的水平速度随位置变化曲线；(d)为四旋翼无人机的垂直速度随位置变化曲线。
具体实施方式
[0067]
下面通过参考附图描述的实施例是示例性的，旨在用于解释本发明，而不能理解为对本发明的限制。
[0068]
参照图1-5所示，本发明一种四旋翼无人机栖停机动轨迹优化方法，包括如下步骤：
[0069]
步骤一、四旋翼无人机动力学建模；
[0070]
本实施例中，选用四旋翼无人机的质量m为0.235kg，转动惯量i为0.002kg
·
m2，相
邻两螺旋桨转轴间距l为0.15m，即螺旋桨力臂为0.075m。
[0071]
坐标系选定：四旋翼无人机建模所需的坐标系，分别是地面坐标系ogxgygzg和机体坐标系obxbybzb；两坐标系的相对关系由滚转角φ、俯仰角θ和偏航角ψ三个角度来描述；地面坐标系是固定于地球的惯性坐标系，机体坐标系则是固定于无人机的坐标系，坐标系中心ob位于无人机质心，xb位于无人机对称面内指向前，zb位于无人机对称面内指向上，yb的确定满足右手坐标系。
[0072]
四旋翼无人机纵向运动的动力学方程如下所示
[0073][0074][0075][0076]
i为四旋翼无人机关于yb轴的转动惯量，m为无人机合力矩矢量在地面坐标系yg轴的分量。
[0077]
步骤二、开环运动轨迹生成
[0078]
1.基于时间的运动轨迹求解
[0079]
四旋翼无人机栖停问题可以简化为二维平面内的纵向运动，因此，忽略无人机在yg轴的位移，仅考虑无人机在xg轴和zg轴的位移运动以及旋转运动。因此，无人机纵向动力学方程可表述如下：
[0080][0081][0082][0083]
其中，f
x
为合外力在地面坐标系xg轴的分量，fz为合外力在地面坐标系zg轴的分量，m为无人机合力矩矢量在地面坐标系yg轴的分量；i为螺旋桨计数序号为，i＝1，2，3，4；fi为螺旋桨i的推力，mi为螺旋桨i的扭矩；u为无人机质心速度矢量在地面坐标系xg轴的分量，w为无人机质心速度矢量在地面坐标系zg轴的分量，q为无人机角速度矢量在地面坐标系yg分量；i为四旋翼无人机关于机体坐标系yb轴的转动惯量，m为无人机的质量；
[0084]
将前述格式改写为：
[0085][0086][0087][0088]
改写各式表明，四旋翼无人机某一时刻的速度变化率由当前时刻的推力和俯仰角所决定，而俯仰角加速度仍由推力所决定。因此，当给定无人机的各轴推力随时间变化曲线时，则可以获得无人机的速度、角速度随时间变化曲线。进一步地，通过沿时间积分，就可以获得无人机的位移与俯仰角随时间变化曲线。具体表达式为
[0089]
[0090][0091][0092][0093][0094][0095]
式中，u0为t＝0时刻的u值，w0为为t＝0时刻的w值，q0为为t＝0时刻的q值。x0、z0分别为t＝0时刻的坐标值，θ0分别为t＝0时刻的俯仰角。
[0096]
2.基于距离的运动轨迹求解
[0097]
由轨迹求解方法可知，给定初始值以及推力时间序列的前提下，即可获得开环运动轨迹。但是，实际飞行中，往往无法获取飞行时间而是给定飞行距离即给定起始位置与目标位置，因此，本发明未采用相对时间的推力序列而是采用基于距离的推力序列作为求解输入。轨迹求解过程中，根据当前时刻的坐标位置，采用插值方法求解当前时刻的推力。具体步骤如下：
[0098]
1)问题设定：给定轨迹优化的起始位置、目标位置，确定运动约束(等式约束与不等式约束)；运动约束包括位置、速度、姿态角、角速度；
[0099]
2)推力设定：在给定飞行距离内进行划分，设定采样点数n+1，将轨迹均匀的划分为n段，采用随机取样方法设定推力序列{f1(xj),f2(xj),f3(xj),f4(xj)}，j为采样点序号且j＝1～n+1，采用样条方法生成相对于距离坐标的推力曲线；
[0100]
3)轨迹生成：采用时间推进方法求解飞行轨迹，当前时刻的推力由当前时刻对应的位置坐标在推力序列{f1(xj),f2(xj),f3(xj),f4(xj)}插值而来；
[0101]
4)截止条件：当求解轨迹的水平坐标与目标点水平坐标一致时，轨迹求解终止；
[0102]
步骤三、轨迹优化
[0103]
1.约束设置
[0104]
四旋翼无人机在垂面栖停运动过程包含的约束为位置、速度、姿态角、角速度，需要满足运动过程中最大需要推力小于电机最大推力且着陆时满足速度、俯仰角、位置误差等约束，具体表述如下：
[0105]
1)动力约束：轨迹优化过程中，任意时刻的推力输出必须小于单轴最大推力f
max
；
[0106]
2)俯仰角约束：无人机在与垂面接触时刻，四旋翼无人机的俯仰角θ
des
为-π/2，确保无人机将其栖停装置朝向垂面；
[0107]
3)速度约束：无人机在与垂面接触时刻，四旋翼无人机垂直壁面速度u
des
范围为0.8m/s～1.2m/s，法向速度w
des
范围为-0.2m/s～0.2m/s；u
des
和w
des
的取值范围取决于步骤2)中栖停装置的速度包线。
[0108]
4)位置约束：无人机在与垂面接触时刻，四旋翼无人机降落位置zf与目标位置z
des
的高度误差不超过0.05m。
[0109]
2.罚函数定义
[0110]
栖停机动轨迹包含速度、俯仰角、位置误差等约束，罚函数方法可以将含约束优化
问题转换为无约束优化问题。本节通过构建罚函数获得满足运动约束的飞行轨迹，构建罚函数的原则应保证当罚函数趋近于0时，运动轨迹满足目标约束，因此，本节构建罚函数包括了性能函数、目标约束函数以及动力约束函数，表达式如下：
[0111]
cost＝j1+j2+j3[0112]
式中，j1为性能函数，j2为目标约束，j3为动力约束，各约束表达式如下：
[0113]
j1＝∑(t
·
v)
·
δt
[0114]
j2＝(u
f-1)2+(w
f-0)2+(θ
f-π/2)2[0115]
j3＝∑max{fi(t)-f
max
,0}
[0116]
3.构建混合优化求解器。
[0117]
基于步骤二中建立的基于距离的推力序列{f1(xj),f2(xj),f3(xj),f4(xj)}j＝1～n+1，通过罚函数结合数值优化算法来获得运动约束与动力学约束的可行轨迹；轨迹优化流程步骤如下：
[0118]
1.设定运动状态初始值。设定u0＝0，w0＝0，q0＝0，θ0＝0。x0、z0分别为t＝0时刻的坐标值，设置为-2m和-1m。
[0119]
2.设定设计变量初始值即优化设计样本。将{f1(xj),f2(xj),f3(xj),f4(xj)},j＝1～10，定义f1(xj),f2(xj)的离散序列为prop1_guess，同样，定义f3(xj),f4(xj)的离散序列为prop2_guess。prop_guess的生成公式如下，该公式中，第一个参数为0.25*mg，该参数的设置目的在于保证初始推力恒等于重力，符合悬起始条件。后续[1.0+0.2*rand(1,9)]的设置，共计9个变量，是在0.25*mg基础上添加了
±
20％的随机变化量，用以生成随机的初始值。prop_guess共计生成10维的向量
[0120]
prop_guess＝0.25*m*g,0.25*m*g*[1.0+0.2*rand(1,9)]
[0121]
在本发明实施例中，所生成的序列如下所示，f1(xj),f2(xj)的离散序列为prop1_guess，同样，f3(xj),f4(xj)的离散序列为prop2_guess。该序列最终将作为优化设计的设计变量的初始样本。
[0122]
prop1_guess＝[1.183 1.396 1.956 1.698 2.037 1.518 2.080 0.870 1.243 1.181]；
[0123]
prop2_guess＝[0.861 2.000 1.784 1.520 1.262 1.777 1.104 1.573 1.214 1.341]；
[0124]
3.搭建优化设计框架。本发明实施例采用遗传优化算法开展优化设计工作，其中，优化目标为步骤三所构造的罚函数，初始值设定x0、z0分别为-2m和-1m，且u0＝0，w0＝0，q0＝0，θ0＝0。设计变量为prop1_guess和prop2_guess，由此，可以按照流程图所示进行优化设计迭代。
[0125]
4.当罚函数数值小于阈值时，结束优化，否则，重复进行步骤2和步骤3。阈值设定的原则是：设当前共计进行i次优化迭代，则产生i个优化设计结果；读取当前优化结果opti与上一次优化结果opt
i-1
，若|opt
i-opt
i-1
|/|opt
i-1
|＜δ,则认为优化过程收敛并结束优化过程；δ是人为设定的收敛误差，通常为一个量级为1％或1
‰
的数值。
[0126]
迭代20次，优化设计结束，计算结果如图4与图5所示。
[0127]
结合计算过程，本发明实施例采用的罚函数结合数值优化的方式能够较好的得出优化设计结果，优化结果满足动力学约束、运动状态约束与最大推力约束。此外，从算法角
度来看，采用遗传算法具有较好的全局收敛性，降低了对设计样本的依赖，能够在全局进行寻优。从计算效率来看，本发明实施例中，优化过程中迭代20次得到最优结果，相较于cn113342056a和cn110308699a专利中所应有的山哥搜索算法，计算量更小，寻优效率更高。
[0128]
尽管上面已经示出和描述了本发明的实施例，可以理解的是，上述实施例是示例性的，不能理解为对本发明的限制，本领域的普通技术人员在不脱离本发明的原理和宗旨的情况下在本发明的范围内可以对上述实施例进行变化、修改、替换和变型。