一种机械臂系统的事件触发容错控制方法

1.本发明属于自动化技术及控制领域，具体涉及一种机械臂系统的事件触发容错控制方法。


背景技术：

2.机械臂系统的自适应容错控制是一种能够自行消除故障对机械臂系统造成的影响，使其恢复到合理性能指标的控制技术。在实际控制系统中，控制信号通常通过执行器部件传递给设备。如果执行器发生突然故障或部分失效而忽略，将会损害系统性能，甚至导致系统不稳定或灾难性事故。近年来人们研究了各种容错控制(ftc)方法，以解决文献[1-4]中提出的控制问题。但需要注意的是，上述致动器故障补偿结果均要求控制信号连续传输至致动器，因此可能会占用通信信道的大量容量。最近，有人提出了事件触发控制(etc)来减少信号传输，同时保持满意的系统性能。在[5]中，提出了一种基于神经网络的非线性系统自适应etc。在[6]，[7]中，通过引入基于逻辑的切换机制，提出了一种新的切换etc策略。然而，据作者所知，在考虑有限时间下具有未知执行器故障的etc方面还没有结果。因此，本文研究了一类在事件触发机制下的不确定非线性系统的有限时间自适应容错控制问题。
[0003]
参考文献
[0004]
[1]l.zhang and g.yang.observer-based fuzzy adaptive sensor fault compensation for uncertain nonlinear strict-feedback systems.ieee transactions on fuzzy systems,26(4):2301
–
2310,2017.
[0005]
[2]f.wang andx.zhang.adaptive finite time control of nonlinear systems under time-varying actuator failures.ieee transactions on systems,man,and cybernetics:systems,49(9):1845
–
1852,2018.
[0006]
[3]j.zhang and g.yang.robust adaptive fault-tolerant control for a class of unknown nonlinearsystems.ieee transactions on industrial electronics,64(1):585
–
594,2016.
[0007]
[4]w.liu,x.qi,j.lu,x.jia,and p.li.finite-time fault-tolerant control for nonlinear systems with input quantization and its application.ieee transactions on circuits and systems ii:
[0008]
expressbriefs,67(7):1249
–
1253,2019.
[0009]
[5]y.wang,c.lim,and p.shi.adaptively adjusted event-triggering mechanism on fault detection for networked control systems.ieee transactions on cybernetics,47(8):2299
–
2311,2016.
[0010]
[6]y.li and s.tong.adaptive neural networks decentralized ftc design for nonstrict-feedback nonlinear interconnected large-scale systems against actuator faults.ieee transactions on neuralnetworks and learning systems,28(11):2541
–
2554,2016.
[0011]
[7]g.yang and h.wang.fault detection and isolation for a class of uncertain state-feedback fuzzy control systems.ieee transactions on fuzzy systems,23(1):139
–
151,2014.
[0012]
[8]l.xing,c.wen,z.liu,h.su,andj.cai.adaptive compensation for actuator failures with event-triggered input.automatica,85:129
–
136,2017.
[0013]
[9]c.zhang and g.yang.event-triggered adaptive output feedback control for a class of uncertain nonlinear systems with actuator failures.ieee transactions on cybernetics,50(1):201
–
210,2018.
[0014]
[10]y.li,d.ba,and s.tong.event-triggered control design for nonlinear systems with actuator failures and uncertain disturbances.international journal of robust and nonlinear control,29(17):6199
–
6211,2019.
[0015]
[11]f.wang,b.chen,x.liu,and c.lin.finite-time adaptive fuzzy tracking control design for nonlinear systems.ieee transactions on fuzzy systems,26(3):1207
–
1216,2017.
[0016]
[12]y.xie and q.ma.adaptive event-triggered neural network control for switching nonlinear systems with time delays.ieee transactions on neural networks and learning systems,doi:10.1109/tnnls.2021.3100533,2021.
[0017]
[13]w.sun,j.zhao,w.sun,j.xia,and z.sun.adaptive event-triggered global fast finite-time control for a class of uncertain nonlinear systems.international journal of robust and nonlinear control,30(9):3773
–
3785,2020.


技术实现要素：

[0018]
为解决上述问题，本发明公开了一种机械臂系统的事件触发容错控制方法。
[0019]
实现本发明目的的技术解决方案，包含以下步骤：
[0020]
步骤1，介绍了机械臂系统的数学模型；
[0021]
步骤2，建立一种更一般的具有不确定参数、未知控制方向的严格反馈非线性系统；
[0022]
步骤3，提出事件触发机制来减轻控制器与执行器之间的通信负担；
[0023]
步骤4，事件触发控制器和参数自适应律的设计与稳定性分析；
[0024]
步骤5，对步骤1所提出的机械臂系统进行仿真研究，验证本研究所提出控制方法的有效性。
[0025]
本发明进一步优选在于：所述步骤1中，介绍了机械臂系统的数学模型；
[0026]
使用了一个包含电机动力学的单连杆机械手，它由下列动力学方程控制:
[0027][0028][0029]
定义x1＝q,x3＝v，于是系统机械臂系统可被重新描述为：
[0030][0031]
定义机械臂中变量和参数，q为连杆的角度位置；为连杆的角速度；为连杆的加速度；d为机械惯性；b为关节处粘滞摩擦系数；n为连杆的重力；v为由电气子系统引起的转矩；m为电枢电感；h为电枢电阻；l为反电动势系数；uf为连杆的控制力；
[0032]
控制目标是为机械臂系统构造一种在事件触发机制下的有限时间自适应控制方法，控制器中即使存在未知的执行器故障，仍然可以保证机械臂系统的稳定性。
[0033]
本发明进一步优选在于：所述步骤2中，建立了如下具有不确定参数和未知控制方向的非线性系统的数学模型：
[0034][0035]
式中uf∈r分别为状态向量和控制输入。和b分别为已知光滑非线性函数和未知非零控制增益；θ为未知的系统参数；di(t)为有界的外部扰动，满足|di(t)|≤di,，其中为di＞0为常数；本发明的执行器故障既有偏置故障又有失效故障；
[0036]
执行机构故障模型如下:
[0037]
uf(t)＝(1-s)v(t)+u0(t),t≥tf[0038]
其中v(t)为事件触发输入；s为未知控制失效率，满足0≤s＜1；u0(t)为未知时变函数表示偏移故障；tf为执行器故障开始的时间。
[0039]
可将原系统重新描述为：
[0040][0041]
本发明进一步优选在于：所述步骤3中，采用时变阈值策略设计事件触发机制，事件触发机制如下：
[0042][0043]
t
k+1
＝inf{t＞tk||e(t)|≥β|v(t)|+η}
[0044]
ω(t)＝(1+λ1(t)β)v(t)+λ2(t)η
[0045][0046]
其中ω(t)为待设计的自适应事件触发控制器；tk为控制器更新时间，当tk≤t＜t
k+1
，执行器保持为一个常数一旦发生触发，控制信号v(t)将变成ω(t
k+1
)；e(t)＝ω(t)-v(t)为测量误差；0＜β＜1,0＜η＜1为待设计的参数；|λ1(t)|≤1,|λ2(t)|≤1。
[0047]
本发明进一步优选在于：所述步骤4中，设计了事件触发控制器和各参数的自适应律：
[0048]
其中事件触发控制器的设计为：
[0049][0050]
各参数的自适应律设计为：
[0051][0052]
并且在稳定性分析部分证明了本发明所设计的控制器可以保证闭环系统中所有信号都是半全局有限时间稳定的。
[0053]
本发明进一步优选在于：所述步骤5中，对步骤1所提出的机械臂系统进行仿真，验证了本发明所提自适应容错方法的有效性。
[0054]
本发明与现有技术相比，其显著优点为：
[0055]
(1)本文所提出的控制器能使系统达到有限时间稳定，与非有限时间控制方法相比，本文的控制方法能提高在实际系统中的控制效率。
[0056]
(2)研究了具有未知时变函数的不确定执行器故障。本文的ftc控制方法方法更有用。并且本设计提出的新的容错控制方法能保证控制过程的安全性。
[0057]
(3)事件触发输入信号能将连续信号转化为离散信号以保证系统的有限时间稳定；在etc方案的设计中，该控制器允许执行器以分段常数的形式以不规则的间隔接收控制信号，进一步有效地消除冗余项，避免繁琐，更容易实现。
[0058]
(4)本文考虑的非线性参数化系统在实际工程中比没有不确定参数的系统更为普遍；本文提出的自适应控制方案可应用于一类参数不确定的非线性系统。
附图说明
[0059]
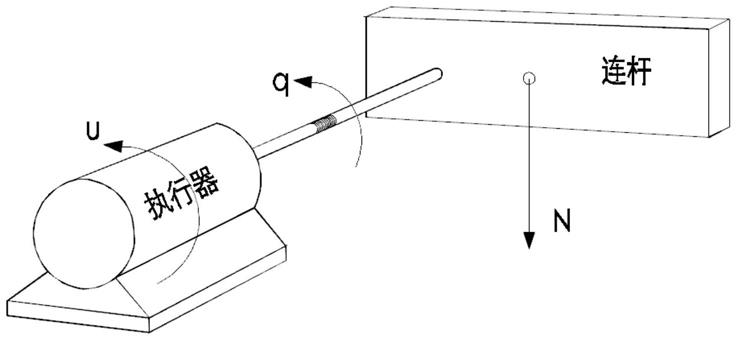
图1是包含电机动力学的单连杆三阶机械臂系统；
[0060]
图2是系统输出信号y和其跟踪信号yr的轨迹；
[0061]
图3是状态变量x2的轨迹；
[0062]
图4是状态变量x3的轨迹；
[0063]
图5是事件触发控制器输入v和执行器输出us的轨迹；
[0064]
图6表示每个事件的时间间隔。
具体实施方式
[0065]
下面结合附图和具体实施方式，进一步阐明本发明，应理解下述具体实施方式仅用于说明本发明而不用于限制本发明的范围。需要说明的是，下面描述中使用的词语“前”、“后”、“左”、“右”、“上”和“下”指的是附图中的方向，词语“内”和“外”分别指的是朝向或远离特定部件几何中心的方向。
[0066]
本实施例提出了一种机械臂系统的事件触发容错控制方法，以保证闭环动态系统
的所有信号都是半全局实际有限时间稳定的。其次，利用所设计的控制器和参数自适应律，有效地解决了参数系统的不确定性和执行器的未知故障问题。最后，以机械臂系统为例进行了仿真，验证了所提出控制技术的有效性。
[0067]
包括以下步骤：步骤1，介绍了机械臂系统的数学模型；
[0068]
机械臂的控制问题是一个有价值的研究课题。机械臂动力学由如下非线性方程定义：使用了一个包含电机动力学的单连杆机械臂系统，如图1所示。它由以下动力学方程控制:
[0069][0070]
系统(1)的变量和参数定义如表1所示。
[0071]
表1：定义机械臂中变量和参数
[0072][0073][0074]
控制目标是为系统(1)构造一种有限时间自适应控制方法，考虑到控制器中执行器的故障，通过引入事件触发控制机制，仍然可以保证机械臂系统的稳定性。
[0075]
在下列步骤中将三阶机械臂系统(1)推广到以下n维非线性系统。
[0076]
步骤2，建立一种更一般的具有不确定参数和未知控制方向的严格反馈非线性系统；
[0077][0078]
式中uf∈r分别为状态向量和控制输入。和b分别为已知光滑非线性函数和未知非零控制增益。θ为未知的系统参数，di(t)为有界的外部扰动，满足|di(t)|≤di,，其中为di＞0为常数。本发明的执行器故障既有偏置故障又有失效故障。
[0079]
执行机构故障模型如下:
[0080]
uf(t)＝(1-s)v(t)+u0(t),t≥t
f (3)
[0081]
可将原系统重新描述为：
[0082][0083]
为了便于控制器的设计，我们定义了如下假设：
[0084]
假设1：扰动di(t)和是有界的，并且i＝1,2,...,n。且存在常数di，使得外部扰动di(t)满足|di(t)|≤di。
[0085]
假设2：参考信号yr(t)及其i阶导数是连续有界的，i＝1,2,...,n，即存在常数y0,y1,y2,...,yn，使得yr(t)以及分别满足|yr(t)|≤y0，
[0086]
步骤3，提出事件触发机制来减轻控制器与执行器之间的通信负担；
[0087]
采用时变阈值策略设计事件触发机制，事件触发机制如下：
[0088][0089]
t
k+1
＝inf{t＞tk||e(t)|≥β|v(t)|+η}
ꢀꢀꢀꢀ
(5)
[0090]
ω(t)＝(1+λ1(t)β)v(t)+λ2(t)η
[0091][0092]
其中ω(t)为待设计的自适应事件触发控制器；tk为控制器更新时间，当tk≤t＜t
k+1
，执行器保持为一个常数一旦发生触发，控制信号v(t)将变成|λ1(t)|≤1,|λ2(t)|≤1ω(t
k+1
)；e(t)＝ω(t)-v(t)为测量误差；0＜β＜1,0＜η＜1为待设计的参数。
[0093]
步骤4，事件触发控制器和参数自适应律的设计与稳定性分析；
[0094]
我们将采用backstepping技术设计事件触发的控制器和参数自适应律。
[0095]
首先，引入下面的坐标变换：
[0096]
z1＝x
1-yr,zi＝x
i-α
i-1
,i＝2,3,...,n (6)
[0097]
第1步：
[0098][0099]
选择如下lyapunov函数
[0100][0101]
其中
[0102]
对式(8)进行求导可得
[0103][0104]
利用young's不等式，可得
[0105][0106]
设置中间控制律和调节函数为
[0107][0108]
将式(10)与式(11)代入式(9)可推导出
[0109]
第2步：
[0110][0111]
选择如下lyapunov函数
[0112][0113]
对式(14)进行求导可得
[0114]
以及
[0115][0116]
利用young's不等式，可得
[0117][0118][0119]
结合(16)，(17)和(18)，v2的导数可以变为
[0120]
[0121]
设置中间控制律和调节函数为
[0122][0123]v2
的导数为
[0124][0125]
第i步：
[0126][0127]
利用young's不等式，可得
[0128][0129]
考虑如下lyapunov函数
[0130][0131]
由(24)可得vi的导数为
[0132][0133]
其中
[0134][0135]
设置中间控制律和调节函数为
[0136][0137]
将(26)代入(25)可得vi的导数为
[0138][0139]
第n步：
[0140][0141]
令b(1-s)＝g，则采用时变阈值策略设计事件触发机制，事件触发机制如下：
[0142]
t
k+1
＝inf{t＞tk||e(t)|≥β|v(t)|+η} (29)
[0143]
ω(t)＝(1+λ1(t)β)v(t)+λ2(t)η
[0144][0145]
其中0＜β＜10＜η＜1|λ1(t)|≤1|λ2(t)|≤1
[0146]
考虑如下lyapunov函数
[0147][0148]
对式(11)进行求导可得
[0149][0150]
利用young's不等式，可得
[0151][0152][0153]
定义
[0154][0155]
结合(31)，(32)和(33)，vn的导数可以变为
[0156][0157]
设置控制律为
[0158][0159]
将(35)代入(34)可得vn的导数为
[0160][0161]
根据[10]中的引理1，可以得到如下不等式
[0162][0163]
参数自适应律设计为
[0164][0165]
结合(36)，(37)和(38)，的导数可以变为
[0166][0167]
接下来，给出了事件触发控制器(29)在存在不匹配扰动和未知执行器故障的情况下保证系统(2)的半全局有限时间稳定的定理。
[0168]
定理1：考虑假设1-2下具有非严格反馈结构的系统(2)和执行器故障模型(3)，将自适应有限时间事件触发控制器(29)，以及实际控制信号(35)和参数自适应律(38)应用于系统，可以保证以下结论成立：
[0169]
(1)闭环系统中的所有信号均是有界的。
[0170]
(2)跟踪误差和观测器误差在有限时间被调整到零的小邻域内。
[0171]
(3)存在一个常数t
′
＞0，使得也就是说，zeno行为不会发生。
[0172]
证明：
[0173]
由young不等式，根据[11]中的引理1、[12]中的引理1可得
[0174][0175][0176]
将(38)代入(37)可得vn的导数为
[0177][0178][0179]
令
[0180][0181]
可得
[0182]
[0183]
①
[0184]
②
[0185]
③
[0186]
根据[11]中的引理4，可得此闭环系统中所有信号都是半全局实际有限时间稳定(sgpfs)的，即跟踪误差可以在有限时间内收敛于原点的一个小邻域，并在t
reach
后保持在该邻域内。
[0187]
接下来，将证明zeno现象不会出现。也就是说，对于任意的q∈z
+
，存在时间t
′
＞0，使得t
q+1-tq≥t
′
。为此，由o(t)＝ξ(t)-u(t)，可得
[0188][0189]
根据式(5.27)，可得ξ是可微的，且不等式成立，其中ι＞0为一个常数。由于o(tq)＝0以及因此t
′
≥(π|u(t)|+a)/ι，于是成功地避免了zeno行为。
[0190]
步骤5，对步骤1所提出的机械臂系统进行仿真研究，验证本研究所提出控制方法的有效性。
[0191]
考虑如下包含电机动力学的单连杆机械臂系统
[0192][0193][0194]
定义x1＝q,x3＝v，于是系统机械臂系统可被重新描述为：
[0195][0196]
其中
[0197][0198]
以及参考信号给出为yr＝sin(0.5t)+sin(1.5t)。执行器在20秒之后开始失效，失效率s＝0.5，偏移故障u0(t)＝cos2(x1)x2。
[0199]
仿真结果如图2-6所示，图2是系统输出信号y和其跟踪信号yr的轨迹；图3是状态变量x2的轨迹；图4是状态变量x3的轨迹；图5是事件触发控制器输入v和执行器输出us的轨迹；图6表示每个事件的时间间隔。由图2-6所得本发明所设计的控制器可保证机械臂系统是半全局实际有限时间稳定(sgpfs)的的。
[0200]
本发明方案所公开的技术手段不仅限于上述实施方式所公开的技术手段，还包括由以上技术特征任意组合所组成的技术方案。