基于障碍物动态虚拟膨胀的智能车辆避碰路径规划方法

control：a nonconvex approach for obstacle avoidance[j].ieee transactions on control systems technology，2017，25(2)：469-484.(rosolia u，bruyne s d和alleyne a g.自动车辆控制：一种非凸的避障方法，ieee控制系统技术杂志，2017年第25卷第2期，第469页到484页)”提出障碍物采用椭圆表示，椭圆长、短半轴分别代表障碍物的长和宽，分别将车辆的半长半宽加倍来增加安全裕度，不能适用于所有交通环境中。
[0008]
综上所述，现有技术存在以下问题：
[0009]
1、参考文献1报道的避碰路径规划算法采用增加矩形安全边际对障碍物进行膨胀的方法来确保规划路径的安全性，但矩形膨胀区域会不仅会使膨胀区域过大，而且矩形轮廓可能会导致规划的路径不平滑。
[0010]
2、文献2将障碍物分解为沿车辆纵轴等距分布的特定半径的圆，会导致路径规划的计算量增大，不利于路径规划的实时性；
[0011]
3、文献3提出将障碍物用椭圆形表示，并将因此障碍物的长宽加倍来实现障碍物的膨胀处理，但是该方法不能根据智能车辆周边的环境信息实时调整椭圆的膨胀尺寸，应用场景受限。
[0012]
障碍物膨胀的形状及尺寸对避碰路径的规划有着至关重要的作用。为了使路径的规划实时性好，障碍物的膨胀形状应当简单，路径规划计算量小；障碍物的膨胀尺寸应该随着交通环境动态变化，在不同的交通环境中，障碍物的膨胀尺寸越小，其占据道路的范围越小，可通行路径范围的增大使智能车辆规划的路径平滑性更好。本发明提出的基于障碍物动态虚拟膨胀的智能车辆避碰路径规划方法不仅对智能车辆路径规划的研究具有明确的理论意义，而且对提高交通出行效率、降低事故发生率具有很强的现实意义。


技术实现要素：

[0013]
本发明要解决的技术问题就是克服上述各种方案的局限性，提出一种基于障碍物动态虚拟膨胀的智能车辆避碰路径规划方法。该方法不仅实现障碍物膨胀尺寸根据相对速度、相对加速度和和偏航角度的动态膨胀，还利用人工势场法对膨胀后的障碍物和道路进行建模，并设立虚拟目标点，推动车辆向前运动，结合梯度下降算法和五次多项式拟合进行路径规划及优化，完成了车辆避让静态障碍物和动态障碍物路径的规划。
[0014]
本发明的目的是这样实现的，本发明提供了一种基于障碍物动态虚拟膨胀的智能车辆避碰路径规划方法，所述规划方法包括以下步骤：
[0015]
步骤1，智能车辆状态信息及周边环境信息的获取
[0016]
通过智能车辆的车载传感器、定位系统和v2x系统获取智能车辆状态信息及周边环境信息；
[0017]
步骤2，参考坐标系的设定
[0018]
以智能车辆几何中心点为原点，以交通流方向为x轴、垂直于x轴的方向为y轴，设定车辆坐标系；
[0019]
设智能车辆开始换道时刻为t0，以t0时刻智能车辆所在道路的最右侧边界为u轴，垂直于u轴的方向为v轴，设定地球坐标系；
[0020]
将智能车辆在t0时刻所在的车道记为原始车道，原始车道的中心线在地球坐标系中的v轴坐标记为v
cr
；并将原始车道左侧相邻车道记为左侧车道，左侧车道的中心线在地球
坐标系中的v轴坐标为v
cl
；
[0021]
将智能车辆沿着地球坐标系u轴方向行驶的速度为纵向速度，智能车辆沿着地球坐标系v轴方向行驶的速度为横向速度；
[0022]
步骤3，障碍物动态虚拟膨胀
[0023]
将智能车辆前方静止物体称为静态障碍物，纵向速度小于智能车辆纵向速度的运动物体称为动态障碍物，静态障碍物和动态障碍物统称为障碍物，进行障碍物动态虚拟膨胀；
[0024]
步骤3.1，将智能车辆的车身形状简化为矩形，并将该矩形的四个角分别记为智能车辆左前角p
lf
、智能车辆右前角p
rf
、智能车辆左后角p
lr
和智能车辆右后角p
rr
，在t0时刻智能车辆左前角p
lf
、智能车辆右前角p
rf
、智能车辆左后角p
lr
和智能车辆右后角p
rr
在车辆坐标系中的坐标分别如下：
[0025][0026][0027][0028][0029]
其中，θ表示智能车辆的初始航向角，l
ego
为智能车辆车身长度，w
ego
为智能车辆车身宽度；
[0030]
步骤3.2，设智能车辆沿着地球坐标系u轴方向行驶的距离为纵向距离，智能车辆沿着地球坐标系v轴方向行驶的距离为横向距离；
[0031]
设智能车辆前方有障碍物，智能车辆在t0时刻开始向左侧车道换道，且经过t时间后智能车辆右前角p
rf
与障碍物发生碰撞，将t0时刻智能车辆几何中心点与障碍物几何中心点的纵向距离记为换道初始纵向安全距离其计算式如下：
[0032][0033]
其中，l
obs
为障碍物的长度，v
obs
为障碍物的纵向速度，a
obs
为障碍物的纵向加速度，v
ego
为智能车辆的纵向速度，a
ego
为智能车辆的纵向加速度；
[0034]
将智能车辆右前角p
rf
与障碍物发生碰撞时，智能车辆几何中心点与障碍物几何中心点的纵向距离记为临界纵向距离临界纵向距离的计算公式如下：
[0035][0036]
步骤3.3，设t0时刻障碍物几何中心点在车辆坐标系中的坐标记为(x0，y0)，将障碍物的形状简化为矩形，使用该矩形的外接椭圆对障碍物进行虚拟膨胀，该外接椭圆划定的
区域即为虚拟膨胀后的障碍物所占用的道路范围，并记为危险区域a
danger
，其中，外接椭圆的长轴σ1和外接椭圆的短轴σ2的计算式分别为：
[0037][0038][0039]
其中，w
obs
表示障碍物的宽度；
[0040]
步骤4，环境建模
[0041]
步骤4.1，设在t0时刻，障碍物几何中心点在地球坐标系中的坐标为(u
obs
(t0)，v
obs
(t0))；
[0042]
将车辆换道避碰过程分为两个阶段，分别记为阶段s1和阶段s2，定义阶段s1为智能车辆从t0时刻开始，换道至左侧车道中心线后继续行驶，直到智能车辆几何中心点超过障碍物几何中心点的纵向距离等于临界纵向距离的位置结束，定义阶段s2为从左侧车道上智能车辆几何中心点超过障碍物几何中心点的纵向距离等于临界纵向距离的位置开始，到障碍物前方的原始车道中心线位置结束；
[0043]
设立局部目标点，并计算局部目标点势能场的场强，计算过程如下：
[0044]
步骤4.1.1，设任意时刻智能车辆的几何中心点的位置为路径点pk，路径点pk在地球坐标系中的坐标为(uk，vk)，判断路径点pk是否处于阶段s1；
[0045]
如果处于阶段s1，则进入步骤4.1.2；
[0046]
如果不处于阶段s1，则进入步骤4.1.3；
[0047]
步骤4.1.2，设在阶段s1中任意一个障碍物的几何中心点位置为第一动态位置p
l1
，第一动态位置p
l1
在地球坐标系中的坐标为(u
l1
，v
l1
)，在左侧车道中心线上选取第一局部目标点p
g1
，第一局部目标点p
g1
在地球坐标系上的坐标为(u
g1
，v
g1
)，若障碍物为静止障碍物时，v
g1
＝v
cl
，若障碍物为动态障碍物时，v
g1
＝v
cl
，进入步骤4.1.4；
[0048]
步骤4.1.3，设在阶段s2中任意一个障碍物的几何中心点位置为第二动态位置p
l2
，第二动态位置p
l2
在地球坐标系中的坐标为(u
l2
，v
l2
)，取消第一局部目标点p
g1
，在原始车道中心线上设立第二局部目标点p
g2
，第二局部目标点p
g2
在地球坐标系中的坐标记为(u
g2
，v
g2
)，若障碍物为静止障碍物时，v
g2
＝v
cr
，若障碍物为动态障碍物时，v
g2
＝v
cr
；
[0049]
步骤4.1.4，引入局部目标点p
gi
，i或为1，或为2，计算局部目标点p
gi
的势能场在路径点pk处的场强u
goali
，i或为1，或为2，计算公式如下：
[0050]ugoali
＝a
goal
[(u
k-u
gi
)2+(v
k-v
gi
)2]
[0051]
其中，a
goal
为局部目标点势能场的场强系数；
[0052]
步骤4.2，对步骤3得到的危险区域a
danger
计算势能场场强，危险区域a
danger
产生的势能场在路径点pk处的场强u
obstacle
的计算公式如下：
[0053]
0＜sd＜sd0[0054]
其中，a
obstacle
为危险区域势能场系数，sd0为危险区域的影响距离，sd为智能车辆几何中心点到危险区域a
danger
边界的最短距离；
[0055]
步骤4.3，将智能车辆周边的道路车道线分成不可跨越车道线和可跨越车道线，且假设车道线是直线，道路车道线产生的势能场在路径点pk处的场强u
road
的计算公式如下：
[0056][0057]
其中，a
road
为道路势能场系数，lw为车道宽度，m1为不可跨越障碍物车道线的系数，m2为可跨越障碍物车道线的系数；
[0058]
步骤4.4，将与局部目标点p
gi
对应的在路径点pk处的智能车辆周边环境综合势能场记为综合势能场，并将综合势能场的场强记为综合场强ui，i或为1，或为2，其计算公式如下：
[0059]
ui＝u
obstacle
+u
road
+u
goali
[0060]
步骤5，避碰路径的生成
[0061]
定义避碰路径如下：以智能车辆从原始车道开始向左侧车道换道时的几何中心点为起点、智能车辆几何中心点到达第二局部目标点p
g2
的位置为终点，由n个避碰路径点组成的避碰路径；
[0062]
步骤5.1，计算综合场强ui的负梯度i或为1，或为2，计算公式如下：
[0063][0064]
其中，表示路径点pk处综合场强ui沿地球坐标系中u轴的变化率，表示路径点pk处综合场强ui沿地球坐标系中v轴的变化率，i或为1，或为2；
[0065]
将路径点pk处的最快下降速度记为v
ki
，i或为1，或为2，并令最快下降速度v
ki
等于综合场强ui的负梯度其计算公式如下：
[0066][0067]
将最快下降速度v
ki
单位化，得到单位最快下降速度i或为1，或为2，计算公式如下：
[0068]
[0069]
将路径点pk的下一个相邻路径点记为路径点p
k+1
，用步长λ乘以单位最快下降速度得出每次迭代前进的距离，并与路径点pk在地球坐标系中的坐标(uk，vk)相加，迭代得到路径点p
k+1
在地球坐标系中的坐标(u
k+1
，v
k+1
)，计算公式如下：
[0070][0071]
步骤5.2，以智能车辆在避碰过程中到达第一局部目标点p
g1
将避碰路径分成两段，分别记为避碰路径1和避碰路径2；将避碰路径1中任意一个路径点记为路径点p
1α
，与路径点p
1α
对应的障碍物位置记为障碍物位置p
1m
，路径点p
1α
处在与第一局部目标点p
g1
对应的综合场强u1的综合势能场中，将避碰路径2中任意一个路径点记为路径点p
2β
，与路径点p
2β
对应的障碍物位置记为障碍物位置p
2n
，路径点p
2β
处在与第二局部目标点p
g2
对应的综合场强u2的综合势能场中，其中α为避碰路径1中的路径点的序号，α＝1，2，
…
，n1，m为避碰路径1中障碍物位置的序列号，m＝1，2，
…
，n1，β为避碰路径2中的路径点的序号，β＝1，2，
…
，n2，n为避碰路径2中障碍物位置的序列号，n＝1，2，
…
，n2，n1+n2＝n；
[0072]
步骤5.3，避碰路径中n个路径点的计算
[0073]
步骤5.3.1，避碰路径1中n1个路径点的计算
[0074]
设路径点p
1α
在地球坐标系中的坐标为(u
1α
，v
1α
)，障碍物位置p
1m
在地球坐标系中的坐标为(u
1m
，v
1m
)，将路径点p
1α
的下一个相邻路径点记为路径点p
1α+1
，将路径点p
1α+1
对应的障碍物位置记为障碍物位置p
1m+1
，路径点p
1a+1
在地球坐标系中的坐标为(u
1α+1
，v
1α+1
)，按照步骤5.1的方法计算得到坐标(u
1α+1
，v
1α+1
)，u
1α+1
和v
1α+1
计算公式如下：
[0075][0076][0077]
设智能车辆避碰路径规划周期为t，障碍物位置p
1m+1
在地球坐标系中的坐标为(u
1m+1
，v
1m+1
)，u
1m+1
和v
1m+1
的计算公式如下：
[0078][0079]v1m+1
＝v
cl
[0080]
记录路径点p
1α+1
，并计算路径点p
1α+1
与第一局部目标点p
g1
之间的第一距离误差δs1，计算公式如下：
[0081]
δs1＝||p
1α+1-p
g1
||
[0082]
若第一距离误差δs1小于或等于阈值δs
min
，进入步骤5.3.2；
[0083]
若第一距离误差δs1大于阈值δs
min
，令p
1α+1
＝pk，p
1m+1
＝p
l1
并返回步骤4.1.1；
[0084]
步骤5.3.2，避碰路径2中n2个路径点的计算
[0085]
设路径点p
2β
在地球坐标系中的坐标为(u
2β
，v
2β
)，障碍物位置p
2n
在地球坐标系中的坐标为(u
2n
，v
2n
)，将路径点p
2β
的下一个相邻路径点记为路径点p
2β+1
，将与路径点p
2β+1
相对应的障碍物位置记为障碍物位置p
2n+1
，路径点p
2β+1
在地球坐标系中的坐标为(u
2β+1
，v
2β+1
)，按照步骤5.1的方法计算得到坐标(u
2β+1
，v
2β+1
)，u
2β+1
和v
2β+1
的计算公式如下：
[0086][0087][0088]
设智能车辆避碰路径规划周期为t，障碍物位置p
2n+1
在地球坐标系中的坐标为(u
2n+1
，v
2n+1
)，u
2n+1
和v
2n+1
的计算公式如下：
[0089][0090]v2n+1
＝v
cr
[0091]
记录路径点p
2β+1
，并计算路径点p
2β+1
与第二局部目标点p
g2
之间的第二距离误差δs2，计算公式如下：
[0092]
δs2＝||p
2β+1-p
g2
||
[0093]
若第二距离误差δs2小于或等于阈值δs
min
，进入步骤5.4；
[0094]
若第二距离误差δs2大于阈值δs
min
，令p
2β+1
＝pk，p
2n+1
＝p
l2
，并返回步骤4.1.1；
[0095]
步骤5.4，避碰队列设定
[0096]
按照步骤5.3.1的方式，从避碰路径1的起点p
11
开始，计算得到避碰路径1中n1个路径点的位置，并将n1个路径点组成避碰路径1的避碰队列[p
11
，p
12
，
…
，p
1α，
，p
1α+1
…
，p
1n1
]，其中避碰路径1的起点p
11
为智能车辆在t0时刻的位置；
[0097]
按照步骤5.3.2的方式，从避碰路径2的起点p
21
开始，计算得到避碰路径2中n2个路径点的位置，并将n2个路径点组成避碰路径2的避碰队列[p
21
，p
22
，
…
，p
2β，
，p
2β+1
，
…
，p
2n2
]，其中避碰路径2的起点p
21
为步骤4.1.2中第一局部目标点p
g1
的位置；
[0098]
将避碰路径1的避碰队列[p
11
，p
12
，
…
，p
1α，
，p
1α+1
，
…
，p
1n1
]和避碰路径2的避碰队列[p
21
，p
22
，
…
，p
2β，
，p
2β+1
，
…
，p
2n2
]合并，得到一个完整的避碰队列p，p＝[p
11
，p
12
，
…
，p
1α
，，p
1α+1
，
…
，p
1n1
，p
21
，p
22
，
…
，p
2β，
，p
2β+1
，
…
，p
2n2
]；
[0099]
步骤5.5，采用五次多项式对完整的避碰队列p中n个路径点进行拟合，得到五次多项式的系数和常数：包括五次多项式的五次项系数c0、五次多项式的四次项系数c1、五次多项式的三次项系数c2、五次多项式的二次项系数c3、五次多项式的一次项系数c4和五次多项式的常数c5；将智能车辆避碰路径中的任意一个点记为p
poly
，p
poly
在地球坐标系中坐标记为
(u
poly
，v
poly
)，(u
poly
，v
poly
)满足下式：
[0100][0101]
优选地，步骤所述智能车辆状态信息包括智能车辆的位置、智能车辆的纵向速度、智能车辆的纵向加速度、智能车辆的横向速度、智能车辆的航向角、智能车辆的长宽信息；智能车辆周边环境信息包括车道宽度、车道线类型、静态障碍物的位置、静态障碍物的长宽、动态障碍物的位置、动态障碍物的纵向速度、动态障碍物的纵向加速度、动态障碍物的长宽信息；
[0102]
优选地，所述时间t按照以下公式确定：
[0103][0104]
其中，w
ego
为障碍物的宽度，u
obs
为智能车辆的横向速度；
[0105]
优选地，所述最短距离sd按照以下方法确定：
[0106]
在危险区域边界上取任意一点记为危险边界点ps，画危险边界点ps与障碍物几何中心点的连线，且将该连线与车辆坐标系x轴正方向之间的夹角记为危险夹角则危险边界点ps的坐标为最短距离sd的计算式如下：
[0107][0108]
与现有技术相比，本发明的有益效果是：
[0109]
1、与障碍物矩形膨胀模型相比，本发明提出的障碍物椭圆膨胀区域所占车道空间更少，为车辆避碰路径的规划提供更多空间，更有利于实现路径的规划。
[0110]
2、与参考文献3中的障碍物椭圆形虚拟膨胀方法相比，本发明提出了障碍物动态虚拟膨胀椭圆模型，并依据换道避碰纵向安全距离，计算膨胀椭圆模型的参数，量化了障碍物膨胀的形状与尺寸。该模型的参数根据车辆相对速度、航向角动态变化，能够更好的适应不同交通环境。
[0111]
3、将障碍物虚拟膨胀模型与人工势场法结合，并利用五次多项式对路径点进行拟合优化，路径规划不仅实时性良好，且规划出的路径平滑且安全。
附图说明
[0112]
图1是本实施例中基于障碍物动态虚拟膨胀的智能车辆避碰路径规划方法整体流程图；
[0113]
图2是本实施例中两个坐标系的示意图；
[0114]
图3是本实施例中智能车辆向左侧换道避碰过程示意图；
[0115]
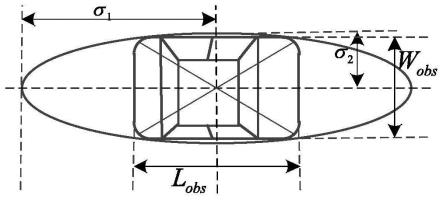
图4是本实施例中障碍物动态虚拟膨胀模型的示意图；
[0116]
图5是本实施例中智能车辆几何中心与危险区域a
danger
边界的最短距离示意图；
[0117]
图6是本实施例中不同类型的车道线示意图；
[0118]
图7是本实施例中智能车辆局部目标点的选取示意图；
[0119]
图8是本实施例中智能车辆前方静态障碍物避碰场景示意图；
[0120]
图9是本实施例中智能车辆在静态障碍物场景中规划的避碰路径；
[0121]
图10是本实施例中智能车辆前方动态障碍物避碰场景示意图；
[0122]
图11是本实施例中智能车辆在动态障碍物场景中规划的避碰路径；
[0123]
图12是本实施例中智能车辆配套的智能车辆避碰路径规划系统框图。
具体实施方式
[0124]
下面结合附图和实施例，对本发明一种基于障碍物动态虚拟膨胀的智能车辆避碰路径规划方法进行详细说明。
[0125]
图1是本实施例的基于障碍物动态虚拟膨胀的智能车辆避碰路径规划方法的流程图，由该图可见，本发明避碰路径规划方法的步骤如下：
[0126]
步骤1，智能车辆状态信息及周边环境信息的获取
[0127]
通过智能车辆的车载传感器、定位系统和v2x系统获取智能车辆状态信息及周边环境信息；
[0128]
所述智能车辆状态信息包括智能车辆的位置、智能车辆的纵向速度、智能车辆的纵向加速度、智能车辆的横向速度、智能车辆的航向角、智能车辆的长宽信息；智能车辆周边环境信息包括车道宽度、车道线类型、静态障碍物的位置、静态障碍物的长宽、动态障碍物的位置、动态障碍物的纵向速度、动态障碍物的纵向加速度、动态障碍物的长宽信息。
[0129]
步骤2，参考坐标系的设定
[0130]
以智能车辆几何中心点为原点，以交通流方向为x轴、垂直于x轴的方向为y轴，设定车辆坐标系；
[0131]
设智能车辆开始换道时刻为t0，以t0时刻智能车辆所在道路的最右侧边界为u轴，垂直于u轴的方向为v轴，设定地球坐标系；
[0132]
将智能车辆在t0时刻所在的车道记为原始车道，原始车道的中心线在地球坐标系中的v轴坐标记为v
cr
；并将原始车道左侧相邻车道记为左侧车道，左侧车道的中心线在地球坐标系中的v轴坐标为v
cl
；
[0133]
将智能车辆沿着地球坐标系u轴方向行驶的速度为纵向速度，智能车辆沿着地球坐标系v轴方向行驶的速度为横向速度。
[0134]
图2是本实施例中两个坐标系的示意图，由图2可见，车辆坐标系和地球坐标系的关系如下：
[0135]
u＝xsinθ+ycosθ
[0136]
v＝xsinθ+ycosθ
[0137]
其中，θ表示智能车辆的初始航向角。
[0138]
步骤3，障碍物动态虚拟膨胀
[0139]
将智能车辆前方静止物体称为静态障碍物，纵向速度小于智能车辆纵向速度的运动物体称为动态障碍物，静态障碍物和动态障碍物统称为障碍物，进行障碍物动态虚拟膨胀。
[0140]
步骤3.1，将智能车辆的车身形状简化为矩形，并将该矩形的四个角分别记为智能车辆左前角p
lf
、智能车辆右前角p
rf
、智能车辆左后角p
lr
和智能车辆右后角p
rr
，在t0时刻智能车辆左前角p
lf
、智能车辆右前角p
rf
、智能车辆左后角p
lr
和智能车辆右后角p
rr
在车辆坐标系中的坐标分别如下：
[0141][0142][0143][0144][0145]
其中，θ表示智能车辆的初始航向角，l
ego
为智能车辆车身长度，w
ego
为智能车辆车身宽度。
[0146]
步骤3.2，设智能车辆沿着地球坐标系u轴方向行驶的距离为纵向距离，智能车辆沿着地球坐标系v轴方向行驶的距离为横向距离。
[0147]
设智能车辆前方有障碍物，智能车辆在t0时刻开始向左侧车道换道，且经过t时间后智能车辆右前角p
rf
与障碍物发生碰撞，将t0时刻智能车辆几何中心点与障碍物几何中心点的纵向距离记为换道初始纵向安全距离其计算式如下：
[0148][0149]
其中，l
obs
为障碍物的长度，v
obs
为障碍物的纵向速度，a
obs
为障碍物的纵向加速度，v
ego
为智能车辆的纵向速度，a
ego
为智能车辆的纵向加速度。
[0150]
所述时间t按照以下公式确定：
[0151][0152]
其中，w
ego
为障碍物的宽度，u
obs
为智能车辆的横向速度。
[0153]
将智能车辆右前角p
rf
与障碍物发生碰撞时，智能车辆几何中心点与障碍物几何中心点的纵向距离记为临界纵向距离临界纵向距离的计算公式如下：
[0154][0155]
步骤3.3，设t0时刻障碍物几何中心点在车辆坐标系中的坐标记为(x0，y0)，将障碍物的形状简化为矩形，使用该矩形的外接椭圆对障碍物进行虚拟膨胀，该外接椭圆划定的区域即为虚拟膨胀后的障碍物所占用的道路范围，并记为危险区域a
danger
，其中，外接椭圆的长轴σ1和外接椭圆的短轴σ2的计算式分别为：
[0156][0157][0158]
其中，w
obs
表示障碍物的宽度。
[0159]
图3是本实施例中智能车辆向左侧换道避碰过程示意图，图4是本实施例中障碍物动态虚拟膨胀模型的示意图。在本实施例中，θ＝15度，x0＝15，y0＝2，σ1＝15，σ2＝2，l
obs
＝3米，w
obs
＝2米，l
ego
＝3米，w
ego
＝2米。
[0160]
步骤4，环境建模
[0161]
步骤4.1，设在t0时刻，障碍物几何中心点在地球坐标系中的坐标为(u
obs
(t0)，v
obs
(t0))。
[0162]
将车辆换道避碰过程分为两个阶段，分别记为阶段s1和阶段s2，定义阶段s1为智能车辆从t0时刻开始，换道至左侧车道中心线后继续行驶，直到智能车辆几何中心点超过障碍物几何中心点的纵向距离等于临界纵向距离的位置结束，定义阶段s2为从左侧车道上智能车辆几何中心点超过障碍物几何中心点的纵向距离等于临界纵向距离的位置开始，到障碍物前方的原始车道中心线位置结束。
[0163]
设立局部目标点，并计算局部目标点势能场的场强，计算过程如下：
[0164]
步骤4.1.1，设任意时刻智能车辆的几何中心点的位置为路径点pk，路径点pk在地球坐标系中的坐标为(uk，vk)，判断路径点pk是否处于阶段s1；
[0165]
如果处于阶段s1，则进入步骤4.1.2；
[0166]
如果不处于阶段s1，则进入步骤4.1.3。
[0167]
步骤4.1.2，设在阶段s1中任意一个障碍物的几何中心点位置为第一动态位置p
l1
，第一动态位置p
l1
在地球坐标系中的坐标为(u
l1
，v
l1
)，在左侧车道中心线上选取第一局部目标点p
g1
，第一局部目标点p
g1
在地球坐标系上的坐标为(u
g1
，v
g1
)，若障碍物为静止障碍物时，v
g1
＝v
cl
，若障碍物为动态障碍物时，v
g1
＝v
cl
，进入步骤4.1.4。
[0168]
步骤4.1.3，设在阶段s2中任意一个障碍物的几何中心点位置为第二动态位置p
l2
，第二动态位置p
l2
在地球坐标系中的坐标为(u
l2
，v
l2
)，取消第一局部目标点p
g1
，在原始车道中心线上设立第二局部目标点p
g2
，第二局部目标点p
g2
在地球坐标系中的坐标记为(u
g2
，v
g2
)，若障碍物为静止障碍物时，v
g2
＝v
cr
，若障碍物为动态障碍物时，v
g2
＝v
cr
。
[0169]
步骤4.1.4，引入局部目标点p
gi
，i或为1，或为2，计算局部目标点p
gi
的势能场在路径点pk处的场强u
goali
，i或为1，或为2，计算公式如下：
[0170]ugoali
＝a
goal
[(u
k-u
gi
)2+(v
k-v
gi
)2]
[0171]
其中，a
goal
为局部目标点势能场的场强系数。
[0172]
步骤4.2，对步骤3得到的危险区域a
danger
计算势能场场强，危险区域a
danger
产生的势能场在路径点pk处的场强u
obstacle
的计算公式如下：
[0173]
0＜sd＜sd0[0174]
其中，a
obstacle
为危险区域势能场系数，sd0为危险区域的影响距离；sd为智能车辆几何中心点到危险区域a
danger
边界的最短距离。
[0175]
所述最短距离sd按照以下方法确定：
[0176]
在危险区域a
danger
边界上取任意一点记为危险边界点ps，画危险边界点ps与障碍物几何中心点的连线，且将该连线与车辆坐标系x轴正方向之间的夹角记为危险夹角危险夹角的取值范围是则危险边界点ps的坐标为最短距离sd的计算式如下：
[0177][0178]
步骤4.3，将智能车辆周边的道路车道线分成不可跨越车道线和可跨越车道线，且假设车道线是直线，道路车道线产生的势能场在路径点pk处的场强u
road
的计算公式如下：
[0179][0180]
其中，a
road
为道路势能场系数，lw为车道宽度，m1为不可跨越障碍物车道线的系数，m2为可跨越障碍物车道线的系数。
[0181]
步骤4.4，将与局部目标点p
gi
对应的在路径点pk处的智能车辆周边环境综合势能场记为综合势能场，并将综合势能场的场强记为综合场强ui，i或为1，或为2，其计算公式如下：
[0182]
ui＝u
obstacle
+u
road
+u
goali
[0183]
图5是本实施例中智能车辆几何与危险区域a
danger
边界的最短距离示意图，展示了通过上述步骤将障碍物进行虚拟膨胀后的效果图，椭圆形的膨胀区域尺寸随着智能车辆的航向角、智能车辆与障碍物的相对速度、智能车辆的尺寸以及障碍物的尺寸确定，其膨胀区域范围是动态变化的。
[0184]
图6是本实施例不同类型的车道线示意图，展示了道路中实线和虚线两种不同的车道线类型，实线代表不可跨越车道线，虚线表示可跨越车道线。
[0185]
图7是本实施例中智能车辆局部目标点的选取示意图。
[0186]
本实施例中，m1＝0.8，m2＝0.2，a
obstacle
＝12，sd0＝0.02，lw＝4米，a
road
＝2，
[0187]
步骤5，避碰路径的生成
[0188]
定义避碰路径如下：以智能车辆从原始车道开始向左侧车道换道时的几何中心点为起点、智能车辆几何中心点到达第二局部目标点p
g2
的位置为终点，由n个避碰路径点组成的避碰路径。
[0189]
步骤5.1，计算综合场强ui的负梯度i或为1，或为2，计算公式如下：
[0190]
[0191]
其中，表示路径点pk处综合场强ui沿地球坐标系中u轴的变化率，表示路径点pk处综合场强ui沿地球坐标系中v轴的变化率，i或为1，或为2。
[0192]
将路径点pk处的最快下降速度记为v
ki
，i或为1，或为2，并令最快下降速度v
ki
等于综合场强ui的负梯度其计算公式如下：
[0193][0194]
将最快下降速度v
ki
单位化，得到单位最快下降速度i或为1，或为2，计算公式如下：
[0195][0196]
将路径点pk的下一个相邻路径点记为路径点p
k+1
，用步长λ乘以单位最快下降速度得出每次迭代前进的距离，并与路径点pk在地球坐标系中的坐标(uk，vk)相加，迭代得到路径点p
k+1
在地球坐标系中的坐标(u
k+1
，v
k+1
)，计算公式如下：
[0197][0198]
在本实施例中，步长λ＝0.1。
[0199]
步骤5.2，以智能车辆在避碰过程中到达第一局部目标点p
g1
将避碰路径分成两段，分别记为避碰路径1和避碰路径2；将避碰路径1中任意一个路径点记为路径点p
1α
，与路径点p
1α
对应的障碍物位置记为障碍物位置p
1m
，路径点p
1α
处在与第一局部目标点p
g1
对应的综合场强u1的综合势能场中，将避碰路径2中任意一个路径点记为路径点p
2β
，与路径点p
2β
对应的障碍物位置记为障碍物位置p
2n
，路径点p
2β
处在与第二局部目标点p
g2
对应的综合场强u2的综合势能场中，其中α为避碰路径1中的路径点的序号，α＝1，2，
…
，n1，m为避碰路径1中障碍物位置的序列号，m＝1，2，
…
，n1，β为避碰路径2中的路径点的序号，β＝1，2，
…
，n2，n为避碰路径2中障碍物位置的序列号，n＝1，2，
…
，n2，n1+n2＝n。
[0200]
步骤5.3，避碰路径中n个路径点的计算
[0201]
步骤5.3.1，避碰路径1中n1个路径点的计算
[0202]
设路径点p
1α
在地球坐标系中的坐标为(u
1α
，v
1α
)，障碍物位置p
1m
在地球坐标系中的坐标为(u
1m
，v
1m
)，将路径点p
1α
的下一个相邻路径点记为路径点p
1α+1
，将路径点p
1α+1
对应的障碍物位置记为障碍物位置p
1m+1
，路径点p
1α+1
在地球坐标系中的坐标为(u
1α+1
，v
1a+1
)，按照步骤5.1的方法计算得到坐标(u
1α+1
，v
1α+1
)，u
1α+1
和v
1α+1
计算公式如下：
[0203]
[0204][0205]
设智能车辆避碰路径规划周期为t，障碍物位置p
1m+1
在地球坐标系中的坐标为(u
1m+1
，v
1m+1
)，u
1m+1
和v
1m+1
的计算公式如下：
[0206][0207]v1m+1
＝v
cl
[0208]
记录路径点p
1α+1
，并计算路径点p
la+1
与第一局部目标点p
g1
之间的第一距离误差δs1，计算公式如下：
[0209]
δs1＝||p
1α+1-p
g1
||
[0210]
若第一距离误差δs1小于或等于阈值δs
min
，进入步骤5.3.2；
[0211]
若第一距离误差δs1大于阈值δs
min
，令p
1α+1
＝pk，p
1m+1
＝p
l1
并返回步骤4.1.1。
[0212]
在本实施例中，阈值δs
min
＝0.05。
[0213]
步骤5.3.2，避碰路径2中n2个路径点的计算
[0214]
设路径点p
2β
在地球坐标系中的坐标为(u
2β
，v
2β
)，障碍物位置p
2n
在地球坐标系中的坐标为(u
2n
，v
2n
)，将路径点p
2β
的下一个相邻路径点记为路径点p
2β+1
，将与路径点p
2β+1
相对应的障碍物位置记为障碍物位置p
2n+1
，路径点p
2β+1
在地球坐标系中的坐标为(u
2β+1
，v
2β+1
)，按照步骤5.1的方法计算得到坐标(u
2β+1
，v
2β+1
)，u
2β+1
和v
2β+1
的计算公式如下：
[0215][0216][0217]
设智能车辆避碰路径规划周期为t，障碍物位置p
2n+1
在地球坐标系中的坐标为(u
2n+1
，v
2n+1
)，u
2n+1
和v
2n+1
的计算公式如下：
[0218][0219]v2n+
1＝v
cr
[0220]
记录路径点p
2β+1
，并计算路径点p
2β+1
与第二局部目标点p
g2
之间的第二距离误差δs2，计算公式如下：
[0221]
δs2＝||p
2β+1-p
g2
||
[0222]
若第二距离误差δs2小于或等于阈值δs
min
，进入步骤5.4；
[0223]
若第二距离误差δs2大于阈值δs
min
，令p
2β+1
＝pk，p
2n+1
＝p
l2
，并返回步骤4.1.1。
[0224]
步骤5.4，避碰队列设定
[0225]
按照步骤5.3.1的方式，从避碰路径1的起点p
11
开始，计算得到避碰路径1中n1个路径点的位置，并将n1个路径点组成避碰路径1的避碰队列[p
11
，p
12
，
…
，p
1α，
，p
1α+1
，
…
，p
1n1
]，其中避碰路径1的起点p
11
为智能车辆在t0时刻的位置。
[0226]
按照步骤5.3.2的方式，从避碰路径2的起点p
21
开始，计算得到避碰路径2中n2个路径点的位置，并将n2个路径点组成避碰路径2的避碰队列[p
21
，p
22
，
…
，p
2β，
，p
2β+1
，
…
，p
2n2
]，其中避碰路径2的起点p
21
为步骤4.1.2中第一局部目标点p
g1
的位置。
[0227]
将避碰路径1的避碰队列[p
11
，p
12
，
…
，p
1α，
，p
1α+1
，
…
，p
1n1
]和避碰路径2的避碰队列[p
21
，p
22
，
…
，p
2β，
，p
2β+1
，
…
，p
2n2
]合并，得到一个完整的避碰队列p，p＝[p
11
，p
12
，
…
，p
1α，
，p
1α+1
，
…
，p
1n1
，p
21
，p
22
，
…
，p
2β
，，p
2β+1
，
…
，p
2n2
]。
[0228]
步骤5.5，采用五次多项式对完整的避碰队列p中n个路径点进行拟合，得到五次多项式的系数和常数：包括五次多项式的五次项系数c0、五次多项式的四次项系数c1、五次多项式的三次项系数c2、五次多项式的二次项系数c3、五次多项式的一次项系数c4和五次多项式的常数c5；将智能车辆避碰路径中的任意一个点记为p
poly
，p
poly
在地球坐标系中坐标记为(u
poly
，v
poly
)，(u
poly
，v
poly
)满足下式：
[0229][0230]
至此，基于障碍物动态虚拟膨胀的智能车辆避碰路径规划结束。
[0231]
为了实现该方法，还配套在智能车辆上安装了一个智能车辆避碰路径规划系统，具体见图12。由图12可见，该系统包括环境感知模块和路径规划模块。所述环境感知模块对车载传感器、定位系统和v2x系统接收的信息进行处理，获取智能车辆周边环境信息和智能车辆自身的状态信息，周边环境信息包括车道宽度、车道线类型、静态障碍物的位置、静态障碍物的长宽、动态障碍物的位置、动态障碍物的纵向速度、动态障碍物的纵向加速度、动态障碍物的长宽信息，智能车辆自身的状态信息包括智能车辆的位置、智能车辆的纵向速度、智能车辆的纵向加速度、智能车辆的横向速度、智能车辆的航向角、智能车辆的长宽，并将处理结果发送给路径规划模块；所述路径规划模块包括坐标系设定、障碍物动态虚拟膨胀、环境建模和路径生成策略，其中，步骤1在环境感知模块完成的，步骤2、步骤3、步骤4和步骤5在路径规划模块完成。
[0232]
为了验证本发明的基于障碍物动态虚拟膨胀的智能车辆避碰路径规划方法的有效性，在matlab环境下搭建了静态障碍物和动态障碍物两种场景进行验证。
[0233]
一、静态障碍物场景
[0234]
图8给出了本实施例中智能车辆前方静态障碍物避碰场景，在该静态障碍物避碰场景中，道路是直的，并由可跨越车道线和不可跨越车道线组成。智能车辆以10m/s的速度沿着车流方向行驶，智能车辆前方15m处出现了一个静止障碍物，椭圆形区域为虚拟膨胀后的障碍物所占道路范围，属于危险区域。图9给出了本实施例中智能车辆在静态障碍物场景中规划的避碰路径，从图9中可以看出，智能车辆在静态场景中采用本发明的方法进行路径规划，能够成功避开障碍物。
[0235]
二、动态障碍物场景
[0236]
图10给出了本实施例智能车辆前方动态障碍物避碰场景，在该动态障碍物避碰场
景中，智能车辆以10m/s的速度沿着车流方向行驶，障碍物以5m/s的速度沿着原车道向前行驶，智能车辆换道初始时刻与动态障碍物相距15m，椭圆形区域为虚拟膨胀后的障碍物危险区域，该危险区域随着障碍物一起向前移动。图11给出了本实施例中智能车辆在动态障碍物场景中的避碰路径，从该图可见，智能车辆在动态场景中采用本发明的方法进行路径规划，能够成功避开障碍物。