一种抗干扰自适应力位协调控制方法

1.本发明涉及假手控制技术领域，更具体的说是涉及一种抗干扰自适应力位协调控制方法。


背景技术：

2.近些年，肌电假手的研发进入了突飞猛进的发展阶段，出现了一些商业化假肢产品，如英国苏格兰科技公司touch bionics，德国的ottobock公司，美国motion control、liberating technologies公司，以及国内丹阳假肢厂等出产的假手产品。国内一些大学和研究机构在智能肌电假手方面展开了相关研究，并取得了一定的成果，中国科学技术大学、上海交通大学和深圳先进院着重在肌电信号的识别算法的研究，东南大学、华中科技大学和哈尔滨工业大学重点研究机械结构优化和运动控制算法。目前，因肌电假手缺少力度控制、抓取易受外界干扰等不足，还不能完全满足患者对人工义肢的需求。
3.因此，如何提供一种抗干扰自适应力位协调控制方法是本领域技术人员亟需解决的问题。


技术实现要素：

4.有鉴于此，本发明提供了一种抗干扰自适应力位协调控制方法以解决上述技术问题。
5.为了实现上述目的，本发明提供如下技术方案：
6.一种抗干扰自适应力位协调控制方法，具体步骤如下：
7.以机械假手作为被控对象，基于获取的机械假手的抓取力和期望力对肌电信号进行阻抗控制；
8.通过力觉传感器获得机械假手指尖的力度信息fe，并计算期望的力度信息fd和检测力度信息fe的跟随误差fs；
9.结合假手的跟随误差fs和姿态信息xd，通过阻抗控制计算出期望轨迹姿态xc；
10.基于机械假手的当前各个关节角度信息，利用正运动学计算得到指尖姿态信息xe；
11.将期望轨迹姿态xc和指尖姿态信息xe的跟随误差通过逆运动学计算各个关节期望轨迹角度变化；
12.进一步利用指尖各关节期望轨迹角度和当前位姿信息设计扰动观测器和自适应律，并利用反步法设计控制器；
13.将控制信号发送给所述机械假手。
14.可选的，在上述的一种抗干扰自适应力位协调控制方法中，获取的机械假手的期望轨迹xc步骤如下：
15.通过期望的力度信息fd和检测力度信息fe计算得到跟随误差fs；
16.阻抗控制器的任务其中n,b,k表示阻
抗参数，根据系统力度控制性能设置，由此得：xc＝f(fd,fe,xd)；
17.结合假手期待的力度跟随误差信息fs和姿态信息xd，通过阻抗控制计算出期望轨迹姿态xc，xc＝f(fs,xd)。
18.可选的，在上述的一种抗干扰自适应力位协调控制方法中，利用正运动学通过指尖各关节角度计算得到机械假手的期望位姿信息具体步骤如下：
19.仿生单手指具有4个自由度和3个指段组成；采用dh方法建立了灵巧手的坐标系，得到相邻关节之间的齐次变换矩阵；
20.将各关节参数代入齐次变换矩阵，则指尖相对于坐标系的变换矩阵；
21.根据变换矩阵中的位置变换向量得到单手指指尖位置和手指关节角度之间的关系；
22.通过单手指指尖的运动推导各个关节的指尖的速度关系，构建速度雅克比矩阵；
23.在机器人处于位置控制状态时通过单手指的逆运动学解算获得指尖期望位姿所对应的关节角度，其中t为坐标系转换矩阵，是t的伪逆，进而驱动各个关节使单手指达到期望位姿。
24.可选的，在上述的一种抗干扰自适应力位协调控制方法中，假手在预期的力度fd(t)和姿态xd(t)实现对被抓取物体的指令轨迹跟踪，具体步骤如下：
25.联合5个手指的动力学方程和被抓取物体的动力学方程，建立统一的动力学模型，力位动力学模型其中d
x
(x)质量矩阵，是离心力和哥氏力矢量，g
x
(x)是重力矢量；系统的随机形式写成：
26.dx1(t)＝x2(t)
27.dx2(t)＝m-1
(x1(t))(-c(x1(t))x2(t)-g(x1(t))+u(t)+d(x1(t))d(t)+fd(t)-fe(t))dt+m-1
(x1(t))λ(x1(t))dμ(t)
28.其中：x1(t)＝xo(t)，μ(t)是一维标准维纳过程的时变函数；随机扰动λ(x1(t))dμ(t)是由白噪声ξ(t)引入的；m是干扰系统的参数；其中d
x
(x)质量矩阵，是离心力和哥氏力矢量，g
x
(x)是重力矢量；
29.进一步利用指尖各关节角度和期望位姿信息设计扰动观测器和自适应律，并利用反步法设计控制器；
30.由以下要构建的干扰观测器生成。
31.de2(t)＝(-k2e2(t)+ua(t)+m-1
(x1(t))d(x1(t))mew(t))dt+m-1
(x1(t))λ(x1(t))dμ(t)
32.其中：是估计误差，是w(t)的估计，干扰观测器设计如下：
[0033][0034][0035][0036]
估计误差的动态显示为：
[0037][0038]
设计自适应调律如下：
[0039][0040][0041][0042]
其中，是手指关节1角度的估计，是手指关节2的角度估计，系数ε1＞0,ε2＞0,ε3＞0,ε4＞0,ε5＞0和λ1＞0，λ2＞0；φ2′
(x1(t),xd(t))是手指规划轨迹的已知函数。
[0043]
利用反步法，设计抗干扰自适应控制器如下：
[0044][0045][0046]
其中，k1是线性误差的系数，是系统扰动误差的估计。
[0047]
由李雅普诺夫稳定性判定得到复合闭环系统如下所示：
[0048][0049]
在上述讨论的基础上，得出以下主要结果的定理，即给出了保证复合闭环系统在均方指数稳定的充分条件。
[0050]
经由上述的技术方案可知，与现有技术相比，本发明公开提供了一种抗干扰自适应力位协调控制方法，在多重扰动问题下，尤其是随机扰动下的多灵巧手指控制系统的协调控制问题。在反步控制方案下，针对多手指控制系统，提出了一种抗干扰自适应协调控制
策略。常见的时变干扰通过干扰观测器控制方法消除；另一部分由随机白噪声引起的干扰通过自适应控制方案被消除。然后，根据李雅普诺夫稳定性理论和随机控制系统的基础，保证了跟踪误差系统的均方指数稳定。利用所提出的控制策略对多个手指协同控制具有抗干扰性和鲁棒性。
附图说明
[0051]
为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据提供的附图获得其他的附图。
[0052]
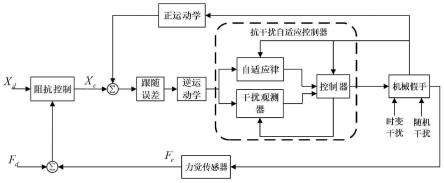
图1为本发明的方法示意图；
[0053]
图2为本发明的实施例被抓取物体的抓取力度fd(t)跟随效果示意图；
[0054]
图3为本发明的实施例被抓取物体的轨迹跟随效果示意图。
具体实施方式
[0055]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0056]
本发明实施例考虑两个仿人型手指进行仿真，以验证本发明设计的控制器的控制性能。参考多臂协作的动力学模型，本实施例建立了两个手指抓取物体的动力学模型，第i个手指的动力学方程的质量矩阵di(qi)
[0057][0058]
其中：
[0059]di11
(qi)＝p
i1
+2p
i2 cos(q
i2
)+2p
i3 cos(q
i3
)+2p
i4 cos(q
i2
+q
i3
)
[0060]di12
(qi)＝p
i5
+p
i2 cos(q
i2
)+2p
i3 cos(q
i3
)+p
i4 cos(q
i2
+q
i3
)
[0061]di13
(qi)＝p
i6
+p
i3 cos(q
i3
)+p
i4 cos(q
i2
+q
i3
)
[0062]di21
(qi)＝d
i12
(qi)
[0063]di22
(qi)＝p
i5
+2p
i3 cos(q
i3
)
[0064]di23
(qi)＝p
i6
+p
i3 cos(q
i3
)
[0065]di31
(qi)＝d
i13
(qi)
[0066]di32
(qi)＝d
i23
(qi)
[0067]di33
(qi)＝p
i6
[0068]
离心力和哥氏力矢量矩阵：
[0069][0070]
其中：
[0071][0072][0073][0074][0075][0076][0077][0078][0079][0080]
重力矢量：
[0081][0082]
其中：
[0083]gi1
(qi)＝p
i7 cos(q
i1
)+p
i8 cos(q
i1
+q
i2
)+p
i9 cos(q
i1
+q
i2
+q
i3
)g
i2
(qi)＝p
i8 cos(q
i1
+q
i2
)+p
i9 cos(q
i1
+q
i2
+q
i3
)
[0084]gi3
(qi)＝p
i9 cos(q
i1
+q
i2
+q
i3
)
[0085][0086]
p
i2
＝m
i3
l
i2
[0087]
p
i3
＝m
i3
l
i1
[0088][0089][0090][0091][0092]
p
i8
＝p
i6
+p
i7
[0093][0094]
相应的jacobian矩阵：
[0095][0096]
其中：
[0097]ji11
(qi)＝-l
i1 sin(q
i1
)-l
i2 sin(q
i1
+q
i2
)-l
i3 sin(q
i1
+q
i2
+q
i3
)
[0098]ji12
(qi)＝-l
i2 sin(q
i1
+q
i2
)-l
i3 sin(q
i1
+q
i2
+q
i3
)
[0099]ji13
(qi)＝-l
i3 sin(q
i1
+q
i2
+q
i3
)
[0100]ji21
(qi)＝l
i1 cos(q
i1
)+l
i2 cos(q
i1
+q
i2
)+l
i3 cos(q
i1
+q
i2
+q
i3
)
[0101]ji22
(qi)＝l
i2 cos(q
i1
+q
i2
)+l
i3 cos(q
i1
+q
i2
+q
i3
)
[0102]ji23
(qi)＝l
i3 cos(q
i1
+q
i2
+q
i3
)
[0103]ji31
(qi)＝j
i32
(qi)＝j
i33
(qi)＝1
[0104]
l
i1
,l
i2
,l
i3
分别表示第i个手指的三个指段的长度，仿真取值l
i1
＝0.05m，l
i2
＝0.03m，l
i3
＝0.02m。
[0105]
被抓取物体的动力学方程如下：
[0106][0107][0108]
其中：mo和io分别为物体的质量和转动惯量，以及
[0109][0110]
其中：l
il
是从第i个指尖到物体质量中心的距离。
[0111]
预定义抓取力度信号：
[0112]
fd(t)＝100n
[0113]
预定义的轨迹信号选择为
[0114][0115]
扰动d(t)的系统参数设置为：
[0116][0117]
选择随机扰动的时变参数作为：
[0118][0119]
φ1(t)和φ2(t)定义为φ1(t)＝10(cos(q
11
(t)))2和φ2(t)＝10(cos(q
11
(t)))2，被抓取对象初始化参数设置为xo(t)＝(-0.006 0.026
ꢀ‑
0.004)。
[0120]
仿真结果如图2-图3所示，被抓取物体的抓取力度跟随效果如图2所示，被抓取物体的轨迹跟随效果如图3所示，结果表明对象系统可以在合理范围内跟踪设计控制器下的预定义抓取力度和状态轨迹，抓取力度跟随误差控制在1％之内，轨迹跟踪相对误差控制0.5％之内。总之，这些仿真结果表明，利用所提出的控制策略实现对多个手指力度和姿态协同控制，并提高抗干扰性和鲁棒性。
[0121]
本说明书中各个实施例采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似部分互相参见即可。对于实施例公开的装置而言，由于其与实施例公开的方法相对应，所以描述的比较简单，相关之处参见方法部分说明即可。
[0122]
对所公开的实施例的上述说明，使本领域专业技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域的专业技术人员来说将是显而易见的，本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下，在其它实施例中实现。因此，本发明将不会被限制于本文所示的这些实施例，而是要符合与本文所公开的原理和新颖特点相一致的最宽的范围。