基于预测控制的水泥分解炉脱硝调控优化系统和方法与流程

1.本发明涉及水泥分解炉烟气脱硝技术，特别是基于预测控制的水泥分解炉脱硝调控优化方法及系统。


背景技术：

2.我国是世界第一大水泥生产国，2019年全年水泥总产量为23.3亿吨，约占世界水泥总产量的55％。随着水泥生产规模的不断扩大，其生产过程带来的污染问题也不断加重。2019年我国水泥生产共消耗约2.6亿吨标准煤，在水泥煅烧过程产生大量二氧化碳和氮氧化物(nox)，其排放的nox占全国工业排放总量的10％～12％，成为我国第三大氮氧化物污染排放源。
3.水泥分解炉内产生的nox主要以燃料型nox为主，分解炉内通常设置sncr脱硝系统以减少nox的排放。目前分解炉内喷氨量的控制主要采用的是pid控制策略，这种控制策略能在一定程度上进行有效控制，但分解炉非线性、大迟滞等特点对pid调节的效果产生很大影响，因此对分解炉内喷氨控制策略进行优化研究非常有必要。
4.预测控制是一种新型控制理论，该算法思路简单、易于实现，在实际工业过程中应用十分广泛。预测控制以采样控制为基础，核心是通过各种类型的预测模型来预测输出。相比于传统pid算法仅考虑下一时刻控制量，预测控制方法计算未来一段时间内系统动态表现的预测值实现控制量的优化，并且同时具有滚动优化、反馈校正等环节，控制效果较为出色。


技术实现要素：

5.发明目的：本发明的目的是提供一种基于预测控制的水泥分解炉脱硝调控优化方法及系统，从而解决水泥厂分解炉内sncr系统喷氨量难以及时准确控制的问题。
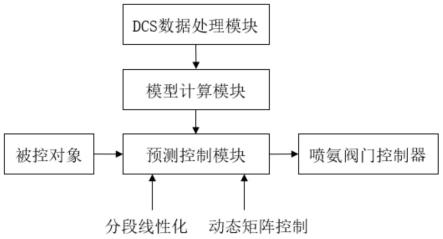
6.技术方案：本发明所述的一种基于预测控制的水泥分解炉脱硝调控优化系统，包括dcs数据处理模块、模型计算模块、预测控制模块、sncr喷氨阀门控制器。
7.所述dcs数据处理模块能够接受水泥厂dcs系统的数据，获取分解炉运行工况数据，将其加工转化为综合工况信息并存储；传输的数据包括：分解炉侧各流量计、浓度分析仪等仪表的测量值，以及喷煤点、下料点、阀门开度等处的控制值。
8.所述模型计算模块接收dcs传递的数据，使用结合卷积神经网络和长短期记忆网络的方法对系统进行辨识，能够建立良好的水泥分解炉运行过程模型，并将计算结果传递给预测控制模块。
9.所述预测控制模块使用分段线性化动态矩阵控制算法，将分解炉sncr还原区域运行过程分段线性化，通过模型计算模块获得各线性子对象的阶跃响应信息，并对其设计自适应动态矩阵控制优化算法，实现水泥分解炉sncr脱硝过程的预测控制。
10.所述sncr喷氨阀门接收预测控制模块指令，调整阀门开度，改变氨水使用量，避免由于氨水量不足而造成脱硝效果不理想或氨水量过多造成氨逃逸及成本升高。
11.所述模型计算模块用于计算分解炉出口nox浓度，该模块设有两路输入数据端口，其中一个数据输入端口接收dcs数据处理模块的综合工况信息，另一个数据输入端口用于直接接收预测计算指令。
12.所述模型计算模块输入的数据包括分解炉内喷煤量、生料下料管下料量、三次风量、三次风温、煤粒径、生料粒径、煤种工业分析数据、石灰石工业分析数据、回转窑烟室气体成分以及分解炉sncr系统氨水浓度及喷氨量，输出为分解炉出口nox浓度。
13.所述模型计算模块中应用的结合卷积神经网络和长短期记忆网络的模型辨识方法是以卷积神经网络(cnn)为基础，提取分解炉运行对象的非线性特征，结合长短期记忆网络(lstm)的时间序列处理能力，消除生产过程时滞性的影响，对分解炉生产过程进行较为精确的建模。
14.对于cnn-lstm模型，其主要结构为：
15.第一隐藏层为卷积层，用于提取不同变量之间的特征关系，卷积核的大小设为3，卷积步长为1，填充层数设为0，使用relu函数作为激活函数；
16.卷积层之后设置池化层，对卷积层得到的结果进行进一步特征选择和信息过滤，采用最大池化(max pooling)方法，输出卷积核内的最大值；
17.在卷积与池化操作之后进行dropout正则化操作，在每次循环中随机选择神经层中的一些单元进行临时隐藏然后再进行该次循环中的训练和优化过程，减少模型过拟合的风险；
18.dropout操作后设置lstm层，用以提取数据的时序特征，消除水泥分解炉运行过程大时滞的不利影响；
19.在lstm层后设置全连接层，使用relu作为激活函数；
20.最后为输出层，输出模型计算得到的nox浓度预测值。
21.所述分段线性化是指通过研究水泥分解炉sncr脱硝系统的动态特性，将脱硝过程分为若干各近似线性的子对象，对每个子对象分别进行计算。
22.所述动态矩阵控制(dmc)以线性子对象的阶跃响应作为预测模型，能够适用于开环稳定、具有纯滞后、非线性特征的复杂过程；该模块同时使用模型预测、反馈校正、滚动优化策略进一步优化控制性能；所述反馈校正是对预测误差的一种修正手段，防止系统运行一段时间后由于模型泛化性降低或其他干扰因素导致预测误差增大，把预测误差在输出端进行补偿；所述滚动优化是指按照确定的性能指标，反复地进行连续、实时地优化。
23.一种基于预测控制的水泥分解炉脱硝调控优化方法，其基本原理为：通过确定未来一段时间内的控制增量δu(i),δu(i+1),
…
,δu(i+k)，使得在该控制作用下，被控对象的预测值y
p
(i)逐步接近期望值r
p
(i)，并以性能评价指标j(i)衡量逼近的效果；所述方法包括以下步骤：
24.(1)通过研究水泥分解炉sncr脱硝系统的动态特性，将脱硝过程分为若干各近似线性的子对象，对每个子对象分别进行计算控制；
25.(2)将分段线性化后各个线性子对象对应的不同幅度的阶跃信号输入到cnn-lstm模型中，得到各组阶跃响应值随样本时间变化的序列，从而获得子对象的模型向量，并由此建立喷氨过程的动态矩阵；
26.(3)计算被控对象在控制增量δu(i),δu(i+1),
…
,δu(i+k)的连续作用下，i时
刻之后未来一段时间内的输出值；
27.(4)将步骤(1)～(3)计算得到的结果代入性能评价指标j(i)，求解目标是使j(i)最小化。通过对j(i)求其关于δuk(i)的偏导数，可得控制增量δuk(i)；
28.(6)对δuk(i)进行反馈校正，消除长时间运行后误差增大的不利效果；
29.(6)将首个控制增量δuk(i)作为当前时刻的控制指令，即当前时刻的控制量为：u(i)＝u(i-1)+δuk(i)。
30.一种计算机存储介质，其上存储有计算机程序，该计算机程序被处理器执行时实现上述的基于预测控制的水泥分解炉脱硝调控优化系统。
31.一种计算机设备，包括储存器、处理器及存储在存储器上并可再处理器上运行的计算机程序，所述处理器执行所述计算机程序时实现上述的基于预测控制的水泥分解炉脱硝调控优化系统。
32.有益效果：与现有技术相比，本发明具有如下优点：
33.1、本发明基于水泥厂历史运行数据，采用数据驱动的建模方法，以水泥分解炉侧可调参数作为模型输入，以分解炉出口nox浓度作为输出，结合卷积神经网络与长短期记忆网络算法构建nox浓度预测模型，通过分段线性化动态矩阵控制方法对sncr脱硝系统喷氨量进行控制，能够较好地应对水泥分解炉运行过程中非线性及时滞等问题；
34.2、本发明的优化方法具有响应速度快、计算量小、控制超调量低以及控制质量高等优点。
附图说明
35.图1为本发明的总体结构图；
36.图2为本发明的模型计算模块框图；
37.图3为本发明的模型训练过程流程图；
38.图4为本发明的预测控制模块结构框图。
具体实施方式
39.下面结合附图对本发明的技术方案作进一步说明。
40.参见图1，一种基于预测控制的水泥分解炉脱硝调控优化控制系统，包括dcs数据处理模块、模型计算模块、预测控制模块、喷氨阀门控制器。dcs数据处理模块与模型计算模块相连接，并向其传递数据；模型计算模块与预测控制模块相连接，在进行预测控制时调用模型，对被控对象的阶跃信号进行计算；预测控制模块输出的指令值传递到喷氨阀门控制器，调节喷氨量，实现水泥分解炉sncr脱硝系统的优化控制。
41.dcs数据传输模块能够接受水泥厂dcs系统的数据，获取分解炉运行工况数据，将其加工转化为综合工况信息并存储。传输的数据包括：分解炉侧各流量计、浓度分析仪等仪表的测量值，以及喷煤点、下料点、阀门开度等处的控制值。
42.模型计算模块用于计算分解炉出口nox浓度，该模块设有两路输入数据端口，其中一个数据输入端口接收dcs数据处理模块的综合工况信息、另一数据输入端口用于直接接收预测计算指令。
43.模型计算模块输入的数据包括分解炉内喷煤量、生料下料管下料量、三次风量、三
次风温、煤粒径、生料粒径、煤种工业分析数据、石灰石工业分析数据、回转窑烟室气体成分以及分解炉sncr系统氨水浓度及喷氨量，输出为分解炉出口nox浓度。
44.模型计算模块中应用的结合卷积神经网络和长短期记忆网络的模型辨识方法，以卷积神经网络(cnn)为基础，结合长短期记忆网络(lstm)的时间序列处理能力，建立cnn-lstm模型，对复杂工业过程进行较为精确的预测。
45.参见图2，为基于预测控制的水泥分解炉脱硝调控优化控制方法的cnn-lstm模型结构框图：
46.对于cnn-lstm模型，其第一隐藏层为卷积层，用于提取不同变量之间的特征关系，卷积核的大小设为3，卷积步长为1，填充层数设为0，使用relu函数作为激活函数；
47.卷积层之后设置池化层，对卷积层得到的结果进行进一步特征选择和信息过滤，采用最大池化(max pooling)方法，输出卷积核内的最大值；
48.在卷积与池化操作之后进行dropout正则化操作，在每次循环中随机选择神经层中的一些单元进行临时隐藏然后再进行该次循环中的训练和优化过程，减少模型过拟合的风险；
49.dropout操作后设置lstm层，用以提取数据的时序特征，消除水泥分解炉运行过程大时滞的不利影响；
50.在lstm层后设置全连接层，使用relu作为激活函数；
51.最后为输出层，输出模型计算得到的nox浓度预测值。
52.以均方根误差(rmse)作为模型训练和测试过程的损失函数，用以评价模型计算效果其计算公式为：
[0053][0054]
参见图3为本发明基于预测控制的水泥分解炉脱硝调控优化控制方法的cnn-lstm模型的训练过程：
[0055]
s1、对dcs系统储存的数据进行预处理，包括数据清洗、特征选择、降维、数据标准化等，并将数据分成相应的训练集和测试集；
[0056]
s2、确定cnn-lstm的模型结构，包括层的设置与连接方式、每层神经元的个数、学习率、正则化参数等；
[0057]
s3、初始化cnn-lstm模型；
[0058]
s4、在训练集上对模型进行训练，计算训练集上模型的均方根误差rmse；
[0059]
s5、在测试集上通过rmse评价模型准确性，若模型误差小于设定的误差阈值则停止训练，否则调整模型初始结构参数，重新进行训练。
[0060]
参见图4，为预测控制模块中分段线性化动态矩阵控制计算方法：
[0061]
分段线性化动态矩阵控制方法的基本原理为：通过确定未来一段时间内的控制增量δu(i),δu(i+1),
…
,δu(i+k)，使得在该控制作用下，被控对象的预测值y
p
(i)逐步接近期望值r
p
(i)。
[0062]
以性能评价指标j(i)衡量逼近的效果：
[0063][0064]
其中yn(i)＝[yn(i+1|i),yn(i+2|i),
…
,yn(i+p|i)]为i时刻的预测值，δu(i)表示控制变化量，r
p
(i)＝[r(i+1),r(i+2),
…
,r(i+p)]为参考轨迹，α,β为权重系数，表示预测误差和控制量的偏重程度。m＝diag[m1,m1,
…
,m
p
]是误差权重矩阵，为一p
×
p维对角矩阵，p是预测时域的长度。n＝diag[n1,n1,
…
,nq]是q
×
q维的控制权重对角矩阵，q是控制时域的长度。
[0065]
分段线化过程通过研究水泥分解炉sncr脱硝系统的动态特性，将脱硝过程分为若干各近似线性的子对象，对每个子对象分别进行计算。
[0066]
将分段线性化后各个线性子对象对应的不同幅度的阶跃信号输入到cnn-lstm模型中，得到各组阶跃响应值随样本时间变化的序列，从而获得子对象的模型向量：a＝[a1,a1,
…
,a
t
],b＝[b1,b1,
…
,b
t
],
…
,其中t称为建模时域。
[0067]
建立起分解炉喷氨脱硝过程的动态矩阵：
[0068][0069]
其中a,b
…
分别是由模型向量a,b
…
组成的p
×
q维动态矩阵。
[0070]
在δu(i),δu(i+1),
…
,δu(i+k)的连续作用下，对于i时刻未来一段时间内的输出值表示为：
[0071][0072]
即y
pn
(i)＝y
p0
(i)+xδuk(i)，x为之前建立的线性对象对应的动态矩阵。
[0073]
评价指标改写为：
[0074][0075]
为使j(i)最小化，通过对其求偏导数，可得控制增量δuk(i)＝(x
t
mx+n)-1xtm[ri-yp0i]。
[0076]
将首个控制增量δuk(i)作为当前时刻的控制作用，则当前时刻的控制量为：u(i)＝u(i-1)+δuk(i)。
[0077]
在每一时刻通过上述方法求得该时刻的控制量，由于通过计算得到的预测输出值会与实际值产生偏差，因此使用下式对预测值进行校正：
[0078]ytrue
(i+1)＝y
pn
(i)+ωe(i+1)
[0079]
其中y
true
(i+1)是经过校正后的输出值，ω为校正向量，e(i+1)为输出误差，计算方法为：e(i+1)＝y(i+1)-y
pn
(i+1|i)。
[0080]
将校正后的计算结果输出，作为当前时刻的控制指令，实现对分解炉喷氨量的分段线性化动态矩阵控制。