一种基于电压控制的轨迹跟踪方法、装置及移动机器人与流程

1.本技术涉及移动机器人技术领域，特别针对一种基于电压控制的轨迹跟踪方法、装置及移动机器人。


背景技术：

2.移动机器人中如扫地机器人、拖地机器人和服务机器人等具备自行走功能的机器人是典型的非完整系统，其运动控制问题是目前研究的重点和难点之一。目前对移动机器人运动控制方案的研究大多建立在“纯滚动无滑动”理想约束的基础上。然而在实际运行时，由于轮胎变形、路面潮湿或结冰、快速转弯等因素影响，容易出现轮子纵向打滑(纵滑)或侧向打滑(侧滑)情况，此时会破坏系统的非完整约束，使移动机器人的运动控制设计变得更为复杂，导致移动机器人失控。
3.在实现过程中，发明人发现传统技术中至少存在如下问题：控制方案均假设扭矩指令作为机器人系统输入，然而在实践中，机器人由具有电压输入的电机驱动，未综合考虑纵滑和侧滑扰动对移动机器人运动控制的影响，降低了移动机器人高速跟踪控制中的运动控制性能。


技术实现要素：

4.基于此，有必要针对由纵滑和侧滑扰动导致的移动机器人轨迹跟踪控制性能降低问题，提供一种基于电压控制的轨迹跟踪方法、装置及移动机器人。
5.为实现上述目的，本发明实施例提供了一种基于电压控制的轨迹跟踪方法，包括如下步骤：
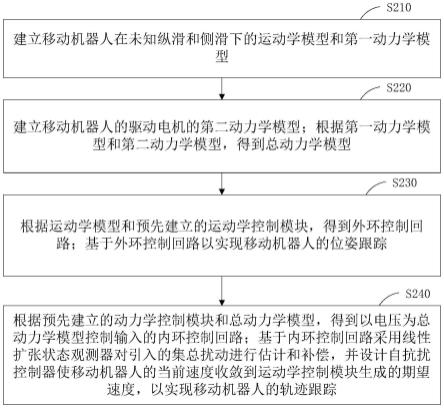
6.建立移动机器人在未知纵滑和侧滑下的运动学模型和第一动力学模型；
7.建立移动机器人驱动电机的第二动力学模型；根据第一动力学模型和第二动力学模型，得到总动力学模型；
8.根据运动学模型和预先建立的运动学控制模块得到外环控制回路；基于外环控制回路以实现移动机器人的位姿跟踪；
9.根据预先建立的动力学控制模块和总动力学模型，得到以电压为总动力学模型输入的内环控制回路；基于内环控制回路采用线性扩张状态观测器对引入的集总扰动进行估计和补偿，并设计自抗扰控制器使移动机器人的当前速度收敛到运动学控制模块生成的期望速度，以实现移动机器人的轨迹跟踪。
10.在其中一个实施例中，基于内环控制回路并采用电压控制方式对引入的集总扰动进行估计和补偿的步骤包括：
11.设计线性扩张状态观测器，通过线性扩张状态观测器对引入总动力学模型的集总扰动进行估计和补偿；其中，集总扰动包括以下信息的任意一种或任意组合：移动机器人未知纵滑和侧滑扰动信息、建模不确定及未知输入扰动信息。
12.在其中一个实施例中，线性扩张状态观测器为通过以下函数得到：
[0013][0014]
其中，分别为状态向量x1、x2、x3的估计值，x1＝z,x3＝ds，z为移动机器人的实际速度，为系统集总扰动，且为系统集总扰动，且为系统集总扰动，且δms为ms的变化量，τd为未知有界可导力矩扰动，为移动机器人发生侧滑时引起的非匹配扰动向量，μ为移动机器人侧滑速度，θ为移动机器人的方向角，η＝[ηvη
ω
]
t
，ηv＝r(ξr+ξ
l
)2为纵滑速度，η
ω
＝r(ξ
r-ξ
l
)(2b)为纵滑引起的横摆率扰动，r为移动机器人驱动轮半径，2b为两驱动轮之间的距离，ξ
l
、ξr分别为移动机器人左右驱动轮纵滑引起的干扰角速度，m、j分别为移动机器人的质量和转动惯量，la、ra、k
t
、kb分别为驱动电机的电枢电感、电枢电阻、转矩常数和反电动势常数，n为机械齿轮减速比；β1、β2、β3分别为线性扩张状态观测器的第一增益、第二增益、第三增益，分别取值为：ωo＞0为观测器带宽；＞0为观测器带宽；ua＝[u
ar u
al
]
t
表示移动机器人右、左驱动轮控制电压。
[0015]
在其中一个实施例中，使移动机器人的当前速度收敛到运动学控制模块生成的期望速度的步骤包括：
[0016]
设计自抗扰控制器，通过自抗扰控制器对移动机器人的当前速度进行控制，以使移动机器人的当前速度收敛到运动学控制模块生成的期望速度。
[0017]
在其中一个实施例中，自抗扰控制器为通过以下函数得到：
[0018][0019]
其中，分别为状态向量x1、x2、x3的估计值，x1＝z,x3＝ds，z为移动机器人的实际速度，为系统集总扰动，且为系统集总扰动，且为系统集总扰动，且δms为ms的变化量，τd为未知有界可导力矩扰动，
为移动机器人发生侧滑时引起的非匹配扰动向量，μ为移动机器人侧滑速度，θ为移动机器人的方向角，η＝[ηvη
ω
]
t
，ηv＝r(ξr+ξ
l
)2为纵滑速度，η
ω
＝r(ξ
r-ξ
l
)(2b)为纵滑引起的横摆率扰动，r为移动机器人驱动轮半径，2b为两驱动轮之间的距离，ξ
l
、ξr分别为移动机器人左右驱动轮纵滑引起的干扰角速度，m、j分别为移动机器人的质量和转动惯量，la、ra、k
t
、kb分别为驱动电机的电枢电感、电枢电阻、转矩常数和反电动势常数，n为机械齿轮减速比，zc为移动机器人的辅助速度，为控制器增益，ωc＞0为控制器带宽，＞0为控制器带宽，
[0020]
在其中一个实施例中，总动力学模型为通过以下函数得到：
[0021][0022]
其中，ua＝[u
ar u
al
]
t
表示移动机器人右、左驱动轮控制电压，表示移动机器人右、左驱动轮控制电压，表示移动机器人右、左驱动轮控制电压，表示移动机器人右、左驱动轮控制电压，表示移动机器人右、左驱动轮控制电压，δms为ms的变化量，τd为未知有界可导力矩扰动，为移动机器人发生侧滑时引起的非匹配扰动向量，μ为移动机器人侧滑速度，θ为移动机器人的方向角，η＝[η
v η
ω
]
t
，ηv＝r(ξr+ξ
l
)/2为纵滑速度，η
ω
＝r(ξ
r-ξ
l
)(2b)为纵滑引起的横摆率扰动，r为移动机器人驱动轮半径，2b为两驱动轮之间的距离，ξ
l
、ξr分别为移动机器人左右驱动轮纵滑引起的干扰角速度，m、j分别为移动机器人的质量和转动惯量，la、ra、k
t
、kb分别为驱动电机的电枢电感、电枢电阻、转矩常数和反电动势常数，n为机械齿轮减速比。
[0023]
在其中一个实施例中，预先建立的运动学控制模块包括通过反步法设计得到的辅助运动学控制器。
[0024]
在其中一个实施例中，辅助运动学控制器为通过以下函数得到：
[0025][0026]
其中vc、ωc分别为设计的移动机器人辅助线速度和辅助角速度，vr、ωr分别为移动机器人参考线速度和参考角速度，k1、k2、k3为辅助运动学控制器控制参数，且均为正常数，e
x
为移动机器人纵向误差，ey为移动机器人侧向误差，e
θ
为移动机器人方向误差。
[0027]
另一方面，本发明实施例还提供了一种基于电压控制的轨迹跟踪装置，包括：
[0028]
第一模型建立单元，用于建立移动机器人在未知纵滑和侧滑下的运动学模型和第一动力学模型；
[0029]
第二模型建立单元，用于建立移动机器人的驱动电机的第二动力学模型；根据第一动力学模型和第二动力学模型，得到总动力学模型；
[0030]
位姿跟踪单元，用于根据运动学模型和预先建立的运动学控制模块，得到外环控制回路；基于外环控制回路以实现移动机器人的位姿跟踪；
[0031]
轨迹跟踪单元，用于根据预先建立的动力学控制模块和总动力学模型，得到以电压为总动力学模型输入的内环控制回路；基于内环控制回路采用线性扩张状态观测器对引入的集总扰动进行估计和补偿，并设计自抗扰控制器使移动机器人的当前速度收敛到运动学控制模块生成的期望速度，以实现移动机器人的轨迹跟踪。
[0032]
另一方面，本发明实施例还提供一种移动机器人，包括移动机器人主体及设置在移动机器人主体上的控制器；控制器用于执行上述任意一项基于电压控制的轨迹跟踪方法。
[0033]
上述技术方案具有如下优点和有益效果：
[0034]
上述基于电压控制的轨迹跟踪方法各实施例中，通过建立移动机器人在未知纵滑和侧滑下的运动学模型和第一动力学模型；建立移动机器人的驱动电机的第二动力学模型；根据第一动力学模型和第二动力学模型，得到总动力学模型；根据所述运动学模型和预先建立的运动学控制模块，得到外环控制回路；基于所述外环控制回路以实现所述移动机器人的位姿跟踪；根据预先建立的动力学控制模块和总动力学模型，得到以电压为总动力学模型输入的内环控制回路；基于所述内环控制回路采用线性扩张状态观测器对引入的集总扰动进行估计和补偿，并设计自抗扰控制器使移动机器人的当前速度收敛到所述运动学控制模块生成的期望速度，以实现所述移动机器人的轨迹跟踪，克服了由纵滑和侧滑扰动导致的移动机器人轨迹跟踪控制性能降低问题，提高了移动机器人高速跟踪控制中的运动控制性能。
附图说明
[0035]
图1为一个实施例中基于电压控制的轨迹跟踪方法的应用环境示意图；
[0036]
图2为一个实施例中基于电压控制的轨迹跟踪方法的第一流程示意图；
[0037]
图3为一个实施例中基于电压控制的轨迹跟踪方法的第二流程示意图；
[0038]
图4为一个实施例中基于电压控制的轨迹跟踪方法的第三流程示意图；
[0039]
图5为一个实施例中基于电压控制的轨迹跟踪方法的控制结构示意图；
[0040]
图6为一个实施例中直行运动轨迹的轨迹跟踪效果曲线示意图；
[0041]
图7为一个实施例中直行运动轨迹的各方向轨迹跟踪效果曲线示意图；
[0042]
图8为一个实施例中直行运动轨迹的位姿跟踪误差曲线示意图；
[0043]
图9为一个实施例中直行运动轨迹的机器人实际速度曲线示意图；
[0044]
图10为一个实施例中直行运动轨迹的各扰动及其估计值曲线示意图；
[0045]
图11为一个实施例中直行运动轨迹的包含驱动电机模型的控制电压输入曲线示意图；
[0046]
图12为一个实施例中直行运动轨迹的无驱动电机模型的控制力矩输入曲线示意图；
[0047]
图13为一个实施例中圆弧运动轨迹的轨迹跟踪效果曲线示意图；
[0048]
图14为一个实施例中圆弧运动轨迹的各方向轨迹跟踪效果曲线示意图；
[0049]
图15为一个实施例中圆弧运动轨迹的位姿跟踪误差曲线示意图；
[0050]
图16为一个实施例中圆弧运动轨迹的机器人实际速度曲线示意图；
[0051]
图17为一个实施例中圆弧运动轨迹的各扰动及其估计值曲线示意图；
[0052]
图18为一个实施例中圆弧运动轨迹的包含驱动电机模型的控制电压输入曲线示意图；
[0053]
图19为一个实施例中圆弧运动轨迹的无驱动电机模型的控制力矩输入曲线示意图；
[0054]
图20为一个实施例中原地旋转运动轨迹的各方向轨迹跟踪特性曲线示意图；
[0055]
图21为一个实施例中原地旋转运动轨迹的位姿跟踪误差曲线示意图；
[0056]
图22为一个实施例中原地旋转运动轨迹的内环速度跟踪曲线示意图；
[0057]
图23为一个实施例中原地旋转运动轨迹的各扰动及其估计值曲线示意图；
[0058]
图24为一个实施例中原地旋转运动轨迹的包含驱动电机模型的控制电压输入曲线示意图；
[0059]
图25为一个实施例中原地旋转运动轨迹的无驱动电机模型的控制力矩输入曲线示意图；
[0060]
图26为一个实施例中基于电压控制的轨迹跟踪装置的方框示意图。
具体实施方式
[0061]
为使本技术领域的人员更好地理解本技术方案，以下将结合本技术实施例中的附图，对本技术实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本技术一部分的实施例，而非全部的实施例。基于本技术中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其它实施例，都应当属于本技术保护的范围。
[0062]
需要说明的是，本技术的说明书和权利要求书及上述附图中的术语“第一”、“第二”等是用于区别类似的对象，而不必用于描述特定的顺序或先后次序。应该理解这样使用的数据在适当情况下可以互换，以便这里描述的本技术的实施例。此外，术语“包括”和“具有”及其任何变形，旨在覆盖不排它的包含，例如，包含了一系列步骤或单元的过程、方法、系统、产品或设备不必限于清楚地列出的那些步骤或单元，而是可包括没有清楚地列出的或对于这些过程、方法、产品或设备固有的其它步骤或单元。
[0063]
另外，术语“多个”的含义应为两个及两个以上。
[0064]
本技术提供的基于电压控制的轨迹跟踪方法，可应用于如图1所示移动机器人。其中，移动机器人包括控制器104和移动机器人主体102，控制器104连接移动机器人主体102，控制器104可用于建立移动机器人在未知纵滑和侧滑下的运动学模型和第一动力学模型；建立移动机器人的驱动电机的第二动力学模型；根据第一动力学模型和第二动力学模型，得到总动力学模型；根据运动学模型和预先建立的运动学控制模块，得到外环控制回路；基于外环控制回路以实现移动机器人的位姿跟踪；根据预先建立的动力学控制模块和总动力
学模型，得到以电压为总动力学模型输入的内环控制回路；基于内环控制回路采用线性扩张状态观测器对引入的集总扰动进行估计和补偿，并设计自抗扰控制器使移动机器人的当前速度收敛到运动学控制模块生成的期望速度，以实现移动机器人的轨迹跟踪。
[0065]
为解决由纵滑和侧滑扰动导致的移动机器人轨迹跟踪控制性能降低问题，在一个实施例中，如图2所示，提供了一种基于电压控制的轨迹跟踪方法，以该方法应用于图1中的控制器104为例进行说明，包括：
[0066]
步骤s210，建立移动机器人在未知纵滑和侧滑下的运动学模型和第一动力学模型。
[0067]
移动机器人可以但不限于是扫地机器人、拖地机器人和服务机器人等具备自行走功能的机器人。第一动力学模型指未包含驱动电机模块的第一动力学模型。
[0068]
示例性的，可定义移动机器人位姿为q＝[x y θ]
t
∈r3×1，(x,y)表示移动机器人几何中心在全局坐标系中的位置，θ表示移动机器人的方向角。在存在纵滑和侧滑扰动情况下，移动机器人的运动学模型可表示为(第一公式)：
[0069]
其中，z＝[vω]
t
，v和ω分别为移动机器人的线速度和角速度；η＝[η
v η
ω
]
t
，ηv＝r(ξr+ξ
l
)2为纵滑速度，η
ω
＝r(ξ
r-ξ
l
)(2b)为纵滑引起的横摆率扰动，r为移动机器人驱动轮半径，2b为两驱动轮之间的距离，ξ
l
、ξr分别为移动机器人左右驱动轮纵滑引起的干扰角速度；为移动机器人发生侧滑时引起的非匹配扰动向量，μ为移动机器人侧滑速度；s(q)具有如下形式：
[0070]
步骤s220，建立移动机器人驱动电机的第二动力学模型；根据第一动力学模型和第二动力学模型，得到总动力学模型。
[0071]
其中，第二动力学模型指考虑驱动电机模型的动力学模型。由于在电机动力学中也存在未建模高频扰动，为了提高系统控制精度，需在控制设计中考虑电机动力学的影响，进而建立移动机器人驱动电机的第二动力学模型，从而根据第一动力学模型和第二动力学模型，得到总动力学模型。
[0072]
步骤s230，根据运动学模型和预先建立的运动学控制模块，得到外环控制回路；基于外环控制回路以实现移动机器人的位姿跟踪。
[0073]
其中，运动学控制模块可根据系统预设得到，控制器可基于双闭环控制方式，其中运动学控制模块为外环控制。运动学控制模块可基于反步法(backstepping)设计得到，通过形成的外环控制回路对移动机器人的位姿数据进行跟踪，驱动移动机器人使其位姿误差数据收敛至第一阈值。示例性地，第一阈值可设置为0，使得移动机器人位姿跟踪误差趋于零。
[0074]
步骤s240，根据预先建立的动力学控制模块和总动力学模型，得到内环控制回路；基于内环控制回路采用线性扩张状态观测器对引入的集总扰动进行估计和补偿，设计自抗扰控制器使移动机器人的当前速度收敛到运动学控制模块生成的期望速度，以实现移动机器人的轨迹跟踪。
[0075]
其中，动力学控制模块可根据系统预设得到，控制器可基于双闭环控制方式，其中
动力学控制模块为内环控制。
[0076]
具体地，控制器可基于内环控制回路，采用电压控制方式代替扭矩控制方式，利用线性扩张状态观测器对引入总动力学模型的集总扰动进行估计和补偿处理，并根据补偿结果驱动移动机器人的当前速度收敛到运动学控制模块生成的期望速度，实现移动机器人内环速度跟踪，进而实现移动机器人轨迹跟踪。
[0077]
需要说明的是，集总扰动可包括以下信息的任意一种或任意组合：移动机器人未知纵滑和侧滑扰动信息、建模不确定及未知输入扰动信息。
[0078]
上述实施例中，控制器通过建立移动机器人在未知纵滑和侧滑下的运动学模型和第一动力学模型；建立移动机器人驱动电机的第二动力学模型；根据第一动力学模型和第二动力学模型，得到总动力学模型；根据运动学模型和预先建立的运动学控制模块，得到外环控制回路；基于外环控制回路以实现移动机器人的位姿跟踪；根据预先建立的动力学控制模块和总动力学模型，得到以电压为总动力学模型控制输入的内环控制回路；基于内环控制回路采用线性扩张状态观测器对引入的集总扰动进行估计和补偿，并设计自抗扰控制器使移动机器人的当前速度收敛到运动学控制模块生成的期望速度，以实现移动机器人的轨迹跟踪，克服了由纵滑和侧滑扰动导致的移动机器人轨迹跟踪控制性能降低问题，提高了移动机器人高速跟踪控制中的运动控制性能。
[0079]
在一个实施例中，总动力学模型为通过以下函数得到：
[0080][0081]
其中，ua＝[u
ar u
al
]
t
表示移动机器人右、左驱动轮控制电压，表示移动机器人右、左驱动轮控制电压，表示移动机器人右、左驱动轮控制电压，表示移动机器人右、左驱动轮控制电压，表示移动机器人右、左驱动轮控制电压，δms为ms的变化量，τd为未知有界可导力矩扰动，为移动机器人发生侧滑时引起的非匹配扰动向量，μ为移动机器人侧滑速度，θ为移动机器人的方向角，η＝[η
v η
ω
]
t
，ηv＝r(ξr+ξ
l
)/2为纵滑速度，η
ω
＝r(ξ
r-ξ
l
)/(2b)为纵滑引起的横摆率扰动，r为移动机器人驱动轮半径，2b为两驱动轮之间的距离，ξ
l
、ξr分别为移动机器人左右驱动轮纵滑引起的干扰角速度，m、j分别为移动机器人的质量和转动惯量，la、ra、k
t
、kb分别为驱动电机的电枢电感、电枢电阻、转矩常数和反电动势常数，n为机械齿轮减速比。
[0082]
示例性地，在纯滚动无滑动理想情况下，移动机器人的动力学模型可描述为(第二公式)：
[0083]
其中为系统正定对称惯性矩阵，m、j分别为移动机器人的质量和转动惯量；为系统离心力和哥氏力矩阵，由于移动机器人的质心与几何中心重合，该项为全零矩阵；g(q)∈r3×1为系统的重力向量，对于在平面运动的移动机器人该项为零向量；为系统输入变换矩阵，θ为移动机器人的方向角，b为两驱动轮之间距离的一半；τ＝[τ
r τ
l
]
t
∈r2×1，τr、τ
l
为系统右、左驱动轮的输入力矩；a(q)＝[-sinθcosθ0]∈r1×3为系统非完整约束矩阵，且s
t
(q)a
t
(q)＝0∈r2×1；为系统约束力项，(x,y)为移动机器人几何中心在全局坐标系中的位置。
[0084]
第一公式与第二公式联立，可得(第三公式)：
[0085]
式中中f2＝s
t
v＝0∈r2×3；；为移动机器人发生侧滑时引起的非匹配扰动向量，μ为移动机器人侧滑速度。
[0086]
考虑动力学模型参数不确定和未知动力学输入干扰，第三公式可重写为(第四公式)：
[0087]
其中δms为ms的变化量，τd∈r2×1为未知有界可导力矩扰动。
[0088]
定义则第四公式可进一步表示为(第五公式)：
[0089]
由于在电机动力学中也存在未建模高频扰动，为了提高系统控制精度，需在控制设计中考虑电机动力学的影响。假定移动机器人由两个相同的有刷直流电机驱动，左、右轮驱动电机的动态方程为(第六公式)：
[0090]
其中，la、ra、k
t
、kb分别为驱动电机的电枢电感、电枢电阻、转矩常数和反电动势常数，n为机械齿轮减速比，τ＝[τ
r τ
l
]
t
表示移动机器人的右、左驱动轮输入力矩，ua＝[u
ar u
al
]
t
,ia＝[i
ar i
al
]
t
分别为驱动电机的控制电压和电枢电流，下标l、r分别表示移动机器人左、右驱动轮，ωw为驱动电机角速度，且有(第七公式)：
[0091]
联立第五公式、第六公式和第七公式可得(第八公式)：
[0092]
式中式中
[0093]
由第八公式可得(第九公式)：
[0094]
式中
[0095]
至此，控制任务为针对具有纵滑和侧滑扰动、模型不确定、未知外部扰动的移动机器人系统，设计驱动电机输入电压ua，使得移动机器人在打滑情况下能精确地实现轨迹跟踪控制。
[0096]
在一个实施例中，预先建立的运动学控制模块包括通过反步法设计得到的辅助运动学控制器。
[0097]
在一个实施例中，辅助运动学控制器为通过以下函数得到：
[0098][0099]
其中vc、ωc分别为设计的移动机器人辅助线速度和辅助角速度，vr、ωr分别为移动机器人参考线速度和参考角速度，k1、k2、k3为辅助运动学控制器控制参数，且均为正常数，e
x
为移动机器人纵向误差，ey为移动机器人侧向误差，e
θ
为移动机器人方向误差。
[0100]
示例性地，针对考虑电机动力学的移动机器人在未知纵滑和侧滑扰动、建模不确定及未知输入扰动下的轨迹跟踪控制，采用反步自抗扰双闭环控制策略，控制结构如图5所示。
[0101]
外环为运动学控制器，以移动机器人的参考位姿与实际位姿的误差为输入，利用反步(backstepping)方法设计辅助运动学控制器，生成辅助线速度和角速度，保证位姿误差渐进收敛到零。内环为动力学控制器，以辅助速度与实际速度的误差为自抗扰动力学控制器的输入并利用线性扩张状态观测器(leso)对动力学集总扰动进行实时估计和补偿，使移动机器人实际运动速度渐进收敛到辅助运动速度，实现其轨迹跟踪控制。
[0102]
其中，预先建立的运动学控制模块的设计过程如下：定义移动机器人期望位姿为qr＝[x
r y
r θr]
t
∈r3×1，满足如下运动学方程(第十公式)：
[0103]
式中zr＝[v
r ωr]
t
，vr为移动机器人前进的参考线速度，ωr为移动机器人本体绕几何中心的参考角速度。
[0104]
定义移动机器人位姿跟踪误差为(第十一公式)：
[0105]
求导可得位姿跟踪误差微分方程为(第十二公式)：
[0106]
采用反步法设计移动机器人辅助运动学控制律，选取以下lyapunov函数(第十三公式)：
[0107]
式中k2为正常数，对v1求导，并将第十二公式代入，整理可得(第十四公式)：
[0108]
设计移动机器人辅助运动学控制输入zc为(第十五公式)：
[0109]
式中vc、ωc分别为设计的移动机器人辅助线速度和角速度，k1、k2、k3为辅助运动学控制律控制参数且均为正常数。
[0110]
将第十五公式代入第十四公式，整理可得(第十六公式)：
[0111]
由此可知在辅助运动学控制输入zc作用下，移动机器人位姿跟踪误差eq趋于零。
[0112]
对于辅助运动学控制器中控制参数k1、k2、k3采用极点配置法进行在线整定。设ξ∈(0,1)为系统阻尼比，ωn＞0为系统自然角频率，选择移动机器人受控系统的期望极点为s1＝-2ξωn,其期望闭环特征多项式可表示为(第十七公式)：
[0113]
将辅助运动学控制输入第十五公式代入系统误差微分方程第十二公式并在平衡点的邻域内用一阶taylor公式展开，可得(第十八公式)：
[0114]
系统矩阵aq的特征多项式为(第十九公式)：
[0115]
比较第十七公式和第十九公式，可得(第二十公式)：
[0116]
由此解得(第二十一公式)：k1＝2ξωn,k3＝2ξωn。
[0117]
当vr→
0时，k2→
∞，为避免该情况发生，选择γ＞0为正常数，则辅
助运动学控制律中控制参数为(第二十二公式)：
[0118]
在一个实施例中，如图3所示，内环速度跟踪处理步骤包括：
[0119]
步骤310，根据预先建立的动力学控制模块和总动力学模型，得到内环控制回路。
[0120]
步骤320，设计线性扩张状态观测器，通过线性扩张状态观测器对引入总动力学模型的集总扰动进行估计和补偿，设计自抗扰控制器使移动机器人的当前速度收敛到运动学控制模块生成的期望速度以实现移动机器人轨迹跟踪。
[0121]
具体而言，控制器可基于线性扩张状态观测器(leso)精确估计纵滑和侧滑、动力学不确定性、未知外部扰动及驱动电机动力学对移动机器人的干扰，通过线性扩张状态观测器对引入总动力学模型的集总扰动进行观测和补偿，进而可通过自抗扰控制器对移动机器人进行内环速度跟踪，使移动机器人的当前速度收敛到运动学控制模块生成的期望速度，实现移动机器人的轨迹跟踪。
[0122]
示例性地，线性扩张状态观测器的设计过程如下：定义状态向量x1＝z,x3＝ds，则第九公式可描述为状态空间形式(第二十三公式)：
[0123]
针对第二十三公式设计线性扩张状态观测器为(第二十四公式)：
[0124][0125]
其中，分别为状态向量x1、x2、x3的估计值，β1、β2、β3为扩张状态观测器的增益，取值为：ωo＞0为观测器带宽。定义扩张状态观测器观测误差通过设计合适的观测器带宽，可使扩张状态观测器观测误差收敛到有界范围。
[0126]
在一个实施例中，如图4所示，内环速度跟踪处理步骤还包括：
[0127]
步骤410，根据预先建立的动力学控制模块和总动力学模型，得到内环控制回路。
[0128]
步骤420，设计线性扩张状态观测器，通过线性扩张状态观测器对引入总动力学模型的集总扰动进行估计和补偿。
[0129]
步骤430，设计自抗扰控制器，通过自抗扰控制器对移动机器人的当前速度进行跟踪，以使移动机器人的当前速度收敛到运动学控制模块生成的期望速度，以实现移动机器人的轨迹跟踪。
[0130]
其中，自抗扰控制器可用于对移动机器人进行内环速度跟踪，进而实现轨迹跟踪。
[0131]
示例性地，自抗扰控制器的设计过程如下：基于移动机器人动力学模型设计自抗扰控制器，以辅助速度zc为输入，实际速度z为输出。基于自抗扰控制方法，如果移动机器人的实际速度收敛到辅助速度，则速度跟踪误差趋于零。定义速度跟踪误差为(第二十五公式)：ez＝z
c-z。
[0132]
由第二十三公式可得(第二十六公式)：
[0133]
基于第二十六公式，自抗扰控制器设计如下(第二十七公式)：
[0134]
其中，为控制器增益，ωc＞0为控制器带宽。
[0135]
应理解的是，虽然图2～图4的流程图中各个步骤按箭头指示依次显示，但这些步骤并非必然按箭头指示顺序依次执行。除非本文中有明确说明，这些步骤的执行并无严格的顺序限制，可以其它顺序执行。而且，图2～图4中至少一部分步骤可包括多个子步骤或多个阶段，这些子步骤或阶段并非必然是在同一时刻执行完成，而是可在不同时刻执行，这些子步骤或阶段的执行顺序也非必然是依次进行，而是可与其它步骤或其它步骤的子步骤或阶段的至少一部分轮流或交替地执行。
[0136]
移动机器人例如为扫地机器人、拖地机器人和服务机器人等具备自行走功能的机器人。本实施例以扫地机器人为例进行说明，验证所设计控制算法的有效性，进行了扫地机器人在未知纵滑和侧滑扰动、未知动力学输入干扰及模型参数不确定下的轨迹跟踪控制仿真试验。由于拖地机器人和服务机器人与扫地机器人的移动方式具有一定相通性，所以在拖地机器人或服务机器人等移动机器人中也同样适用本方法。
[0137]
设定物理参数和驱动电机的相关参数如下：
[0138]
m＝2.7kg,j＝0.033kg
·
m2,r＝0.034m,b＝0.11m,
[0139]
la＝0.02h,ra＝13.5ω,kb＝0.0239v/rad
·
s-1
,
[0140]kt
＝0.0239(n
·
m)/a,n＝54.5
[0141]
扫地机器人参考轨迹初始值设为qr(0)＝[0 0 0]
t
，初始位姿设为q(0)＝[0 0 0]
t
，运动学控制模块参数设为γ＝50、ξ＝0.707，线性扩张状态观测器参数设为ωo＝100，自抗扰控制模块参数设为ωc＝20。
[0142]
为了对所提出控制模块的鲁棒性做进一步研究，假设扫地机器人的未知动力学输入扰动服从正态分布函数：
[0143]
系统不确定部分设为δms＝0.15ms。为了测试所设计控制模块对包含不同频率和幅值的扰动的控制效果，本试验以衰减正弦形式给出纵滑和侧滑扰动，其中左、右驱动轮纵滑角速度扰动：
[0144][0145]
侧滑线速度扰动：其中ts为扰动起始时刻。
[0146]
为验证驱动电机模型对扫地机器人控制性能的影响，将所设计算法与不考虑驱动电机模型的反步自抗扰控制算法(noactuator bcadrc)进行仿真对比。同时，为验证所设计控制算法的控制性能，将其与传统双闭环pid算法(double-closed-loop pid,dclpid)进行比较。其中dclpid外环控制器参数设为：
[0147]kpx
＝1000,k
ix
＝0,k
dx
＝4,k
py
＝1000,k
iy
＝0,k
dy
＝5,k
pθ
＝1000,k
iθ
＝0,k
dθ
＝4,
[0148]
内环控制器参数为：
[0149]kp
＝diag([64,64]),ki＝diag([1,1]),kd＝diag([16,16])。
[0150]
不考虑驱动电机模型的bcadrc算法动力学控制器参数选为：ωc＝8,ωo＝40,运动学控制器参数与所提出的bcadrc运动学控制器参数相同。
[0151]
在实际工况中，扫地机器人的运行轨迹可分为三类：直行、圆弧和原地旋转。下面分别就三种工况下不同控制器的控制效果进行对比分析。
[0152]
直行运动轨迹：根据实际工况，扫地机器人直行可分为两种情况：无障碍物和有障碍物。无障碍物时，扫地机器人以vr＝0.28m/s恒速运行，此时ωr＝0rad/s。检测到障碍物后，线速度每秒对半递减，且线速度递减到0.02m/s以内，即可认为扫地机器人停止运动。经计算，检测到障碍物后，扫地机器人在4s内停止运动，减速过程总位移为0.525m。
[0153]
仿真设置如下：仿真时间30s，采样频率100hz，扫地机器人在0～20s以vr＝0.28m/s恒速运行，其中5～8s发生纵滑，10～13s发生侧滑，15～18s加入集总扰动，即同时发生纵滑和侧滑并考虑建模不确定和未知输入扰动。20s时扫地机器人检测到障碍物，速度递减，在速度递减过程中(21～23s)加入集总扰动。仿真结果如图6～12所示。
[0154]
具体而言，图6中展示了集总扰动下扫地机器人在辅助运动学控制器、线性扩张状态观测器和自抗扰控制器作用下完成的轨迹跟踪任务效果图，可见纵滑、侧滑及集总扰动下，扫地机器人仍能稳定地跟踪直线参考轨迹，且自抗扰控制器相较其它两种控制模块跟踪效果更好、跟踪误差更小。图7和图8为扫地机器人各方向跟踪效果和位姿误差图，在机器人启动时，dclpid和不考虑驱动电机模型的bcadrc算法均有较大初始误差。在恒速运行阶段，dclpid在x方向具有稳态误差。在纵滑、侧滑及集总扰动下，考虑驱动电机模型可提高系统控制精度。相较dclpid控制，所设计的bcadrc算法位姿误差更小、性能更好。扰动消失后，所设计的bcadrc算法可迅速调整使机器人收敛到期望轨迹。图9中为扫地机器人实际速度，考虑驱动电机模型的bcadrc算法在扰动下的速度波动较小、更稳定。图10为线性扩张状态观测器对集总扰动的观测效果，分析可知线性扩张状态观测器对不同频率和幅值的集总扰动均有较好的观测效果，收敛误差小、观测精度较高。图11为控制电压随时间的变化曲线，当存在扰动时，控制模块进行实时调整以抑制扰动对系统影响。图12为不考虑驱动电机模型的bcadrc算法所设计的控制力矩变化情况，控制力矩实时调整，对干扰进行补偿以实现精确的轨迹跟踪控制。
[0155]
圆弧运动轨迹：假定扫地机器人参考轨迹为圆形轨迹，参考速度设为vr＝0.28m/s,ωr＝1rad/s，机器人初始速度设为v＝0m/s,ω＝0rad/s，其余参数同直行运动轨迹。扫地机器人在t＝5～8s时，负载发生缓慢变化，变化量δms＝0.15ms，在10～13s机器人发生纵滑，15～18s发生侧滑，20～23s加入集总扰动，仿真结果如图13～19所示。
[0156]
由图13～15可知，在集总扰动下，扫地机器人在三种控制器的作用下均能精确跟踪参考轨迹，但dclpid会有一定稳态误差，且启动阶段需经较长时间调整才能跟踪期望轨迹。对于自抗扰控制，考虑驱动电机模型的bcadrc算法可提高系统控制性能，减小位姿误差。图16为三种控制算法下扫地机器人实际速度和角速度变化情况，考虑驱动电机模型的
自抗扰控制快速克服了扰动干扰，且超调量小、振荡小，使得线速度和角速度快速收敛到辅助线速度和角速度，控制性能远优于dclpid和不考虑驱动电机模型的bcadrc算法。图17为线性扩张状态观测器对集总扰动的估计，误差较小，可实现对集总扰动实时、精确估计。图18给出了控制电压随时间变化曲线。图19为不考虑驱动电机模型的bcadrc算法所设计的控制力矩变化，通过对控制力矩的实时调整，实现打滑情况下轨迹跟踪控制。
[0157]
原地旋转运动轨迹：在实际工况中会存在扫地机器人原地旋转的情况，针对该情况进行仿真验证。仿真中扫地机器人参考速度设为vr＝0m/s,ωr＝1ra.d2/s2，其余参数参照上述实施例。在t＝5s时，扫地机器人的负载发生缓慢变化，即δms＝0.15ms，在10～13s机器人发生纵滑，15～18s发生侧滑，20～23s加入集总扰动，仿真结果如图20～25所示。
[0158]
由图20和图21可知，在集总扰动下，dclpid会有较大位姿误差。对于自抗扰控制，考虑驱动电机模型可提高系统的控制精度。图22为三种控制算法下，扫地机器人实际速度变化情况，可见自抗扰控制超调小、振荡小。图23表明线性扩张状态观测器可实时准确地对集总扰动进行估计。图24为驱动电机输入电压变化曲线，由于机器人原地旋转，故左右轮输入电压大小相等方向相反，存在扰动时，所设计控制器对控制电压进行调整以抑制扰动对运动控制的影响。图25为不考虑驱动器模型的bcadrc算法所设计的控制力矩变化情况，随着扰动发生，控制力矩相应变化以抑制扰动影响。
[0159]
上述实施例中，考虑扫地机器人在运动过程中受未知纵滑和侧滑干扰、模型不确定、未知输入扰动及驱动电机动态特性影响的问题，依据双闭环控制策略设计辅助运动学控制器和自抗扰控制器，通过线性扩张状态观测器实时估计和补偿扰动，使得机器人实现精确的轨迹跟踪控制。由仿真可知，控制器设计时考虑驱动电机模型可提高扫地机器人的运动控制性能，自抗扰控制可实时估计和补偿扰动，且超调小、振荡小，具有更好的鲁棒性。
[0160]
在一个实施例中，如图26所示，还提供一种基于电压控制的轨迹跟踪装置，包括：
[0161]
第一模型建立单元210，用于建立移动机器人在未知纵滑和侧滑下的运动学模型和第一动力学模型。
[0162]
第二模型建立单元220，用于建立移动机器人驱动电机的第二动力学模型；根据第一动力学模型和第二动力学模型，得到总动力学模型。
[0163]
位姿跟踪单元230，用于根据运动学模型和预先建立的运动学控制模块，得到外环控制回路；基于外环控制回路以实现移动机器人的位姿跟踪。
[0164]
轨迹跟踪单元240，根据预先建立的动力学控制模块和总动力学模型，得到以电压为总动力学模型输入的内环控制回路；基于内环控制回路采用线性扩张状态观测器对引入的集总扰动进行估计和补偿，并设计自抗扰控制器使移动机器人的当前速度收敛到运动学控制模块生成的期望速度，以实现移动机器人的轨迹跟踪。
[0165]
关于基于电压控制的轨迹跟踪装置的具体限定可参见上文中对基于电压控制的轨迹跟踪方法的限定，在此不再赘述。上述基于电压控制的轨迹跟踪装置中各个模块可全部或部分通过软件、硬件及其组合来实现。上述各模块可以硬件形式内嵌于或独立于移动机器人的控制器中，也可以软件形式存储于移动机器人的存储器中，以便控制器调用执行以上各个模块对应的操作。
[0166]
在一个实施例中，还提供了一种移动机器人，包括移动机器人主体及设置在移动机器人上的控制器；控制器用于执行上述任意一项基于电压控制的轨迹跟踪方法。
[0167]
其中，控制器用于执行以下基于电压控制的轨迹跟踪方法的步骤：
[0168]
建立移动机器人在未知纵滑和侧滑下的运动学模型和第一动力学模型；建立移动机器人驱动电机的第二动力学模型；根据第一动力学模型和第二动力学模型，得到总动力学模型；根据运动学模型和预先建立的运动学控制模块，得到外环控制回路；基于外环控制回路以实现移动机器人的位姿跟踪；根据预先建立的动力学控制模块和总动力学模型，得到以电压为总动力学模型控制输入的内环控制回路；基于内环控制回路采用线性扩张状态观测器对引入的集总扰动进行估计和补偿，并设计自抗扰控制器使移动机器人的当前速度收敛到运动学控制模块生成的期望速度，以实现移动机器人的轨迹跟踪。
[0169]
上述实施例中，通过建立移动机器人在未知纵滑和侧滑下的运动学模型和第一动力学模型；建立移动机器人驱动电机的第二动力学模型；根据第一动力学模型和第二动力学模型，得到总动力学模型；根据运动学模型和预先建立的运动学控制模块，得到外环控制回路；基于外环控制回路以实现移动机器人的位姿跟踪；根据预先建立的动力学控制模块和总动力学模型，得到以电压为总动力学模型输入的内环控制回路；基于内环控制回路采用线性扩张状态观测器对引入的集总扰动进行估计和补偿，并设计自抗扰控制器使移动机器人的当前速度收敛到运动学控制模块生成的期望速度，以实现移动机器人的轨迹跟踪，克服了由纵滑和侧滑扰动导致的移动机器人轨迹跟踪控制性能降低问题，提高了移动机器人高速跟踪控制中的运动控制性能。
[0170]
在一个实施例中，还提供一种计算机可读存储介质，其上存储计算机程序，计算机程序被处理器执行时实现上述任一项基于电压控制的轨迹跟踪方法的步骤。
[0171]
在一个示例中，计算机程序被处理器执行时实现以下步骤：
[0172]
建立移动机器人在未知纵滑和侧滑下的运动学模型和第一动力学模型；建立移动机器人驱动电机的第二动力学模型；根据第一动力学模型和第二动力学模型，得到总动力学模型；根据运动学模型、总动力学模型、预先建立的运动学控制模块和预先建立的动力学控制模块，得到外环控制回路；基于外环控制回路以实现移动机器人位姿跟踪；根据预先建立的动力学控制模块和总动力学模型，得到以电压为总动力学模型输入的内环控制回路；基于内环控制回路采用线性扩张状态观测器对引入的集总扰动进行估计和补偿，并设计自抗扰控制器使移动机器人的当前速度收敛到运动学控制模块生成的期望速度，以实现移动机器人轨迹跟踪。
[0173]
本领域普通技术人员可以理解实现上述实施例方法中的全部或部分流程，是可通过计算机程序指令相关的硬件完成，所述计算机程序可存储于一非易失性计算机可读取存储介质中，该计算机程序在执行时，可包括如上述各方法的实施例的流程。其中，本技术所提供的各实施例中所使用的对存储器、存储、数据库或其它介质的任何引用，均可包括非易失性和/或易失性存储器。非易失性存储器可包括只读存储器(rom)、可编程rom(prom)、电可编程rom(eprom)、电可擦除可编程rom(eeprom)或闪存。易失性存储器可包括随机存取存储器(ram)或外部高速缓冲存储器。作为说明而非局限，ram以多种形式可得，诸如静态ram(sram)、动态ram(dram)、同步dram(sdram)、双数据率sdram(ddrsdram)、增强型sdram(esdram)、同步链路(synchlink)dram(sldram)、存储器总线(rambus)直接ram(rdram)、直接存储器总线动态ram(drdram)、以及存储器总线动态ram(rdram)等。
[0174]
以上所述实施例的各技术特征可以进行任意组合，为使描述简洁，未对上述实施
例中的各个技术特征所有可能的组合都进行描述，然而，只要这些技术特征的组合不存在矛盾，都应认为是本说明书记载的范围。
[0175]
以上所述实施例仅表达了本技术的几种实施方式，其描述较为具体和详细，但并不能因此而理解为对发明专利范围的限制。应当指出，对于本领域的普通技术人员而言，在不脱离本技术构思的前提下，还可做出若干变形和改进，这些都属于本技术的保护范围。因此，本技术专利的保护范围应以所附权利要求为准。