一种新型趋近律的板球系统滑模控制方法

1.本发明涉及系统控制领域，尤其涉及一种新型趋近律的板球系统滑模控制方法。


背景技术：

2.板球系统是一个典型的多输入多输出的欠驱动系统，其控制策略可以应用于航天、无人驾驶、平衡车以及导弹轨迹跟踪等控制领域。尽管国内外一些文献采用了反步法以及滑模控制等先进控制来提高系统的跟踪精度，但反步法的抗干扰能力弱，使得系统的鲁棒性不强；滑模控制虽能有效地提高系统的鲁棒性，但其高频抖振一直是滑模控制最突出的一个问题。如何在采用滑模控制来增强鲁棒性的前提下，抑制系统高频抖振、改善系统响应速度以及提高轨迹跟踪精度有待进一步研究；为此，我们提出一种新型趋近律的板球系统滑模控制方法。


技术实现要素：

3.本发明的目的是为了解决现有技术中存在的缺陷，而提出的一种新型趋近律的板球系统滑模控制方法。
4.为了实现上述目的，本发明采用了如下技术方案：
5.一种新型趋近律的板球系统滑模控制方法，该控制方法具体步骤如下：
6.(1)建立板球系统的线性模型：对小球位置信息进行采集，并构建板球系统的线性模型；
7.(2)趋近律设计：设计新型趋近律，同时对该趋近率进行分析；
8.(3)设计新型滑模控制器，并进行稳定性验证：依据新型趋近律以及等效控制律构建新型滑模控制器，并对该新型滑模控制器进行滑模控制方法的稳定性验证。
9.作为本发明的进一步方案，步骤(1)中所述板球系统的线性模型具体构建步骤如下：
10.步骤一：忽略小球滚动中机械结构的内部摩擦力，同时假设小球与板面未分离，且由于小球在工作点附近倾角很小，所以有sinα≈α，sinβ≈β，且其中α是平板x轴方向的倾角，β为y轴方向的倾角；
11.步骤二：对倾角α以及β进行进行线性化处理以生成板球系统模型，其具体模型公式如下：
[0012][0013]
其中，mq为小球质量，rq为小球半径，iq为小球转动惯量，g为重力加速度；
[0014]
步骤三：由公式(1)生成小球状态空间方程，同时由于x轴与y轴对称，其原理一致，
故只分析x轴，同时生成x轴的线性模型，其小球状态空间方程具体如下：
[0015][0016]
其中，
[0017]
作为本发明的进一步方案，步骤三中所述x轴的线性模型具体表示形式如下：
[0018][0019]
其中，g(x)＝-γg，d(t)为干扰项。
[0020]
作为本发明的进一步方案，步骤(2)中所述新型趋近率分析具体步骤如下：
[0021]
第一步：依据板球系统模型生成的各项数据设计相关切换函数，其切换函数具体计算公式如下：
[0022][0023]
其中，c＞0，e＝x
1-x
1d
，x
1d
为期望轨迹；
[0024]
第二步：当系统到达滑模面时，s＝0，易知即有：
[0025][0026]
将式(3)代入式(4)中，得等效控制律：
[0027][0028]
同时，为保证系统快速收敛，且减小系统抖振，设计以下新型趋近律：
[0029][0030]
其中，sgn()为符号函数，k1＞0，0＜λ＜1，k＞1，μ＞1；
[0031]
第三步：对新型趋近律进行分析，由于的存在，当系统状态距离滑模面越远时，收敛速度越快，可保证快速收敛；当距离滑模面较近时，其收敛速度变慢，且由于幂次趋近项的存在，可保证系统平滑地进入滑模面，以达到抑制系统抖振的效果。
[0032]
作为本发明的进一步方案，步骤(3)中所述稳定性验证具体步骤如下：
[0033]
s1：依据公式(6)以及公式(7)设计新型滑模控制器，其新型滑模控制器具体表示形式如下：
[0034][0035]
其中，未知数解释见公式(7)；
[0036]
s2：选取lyapunov函数以对新型滑模控制器的滑模控制方法的稳定性进行验证。
[0037]
作为本发明的进一步方案，s2中所述lyapunov函数具体计算公式如下：
[0038][0039]
由公式(9)可知v≥0；
[0040]
对公式(9)求导得：
[0041][0042]
故整个系统渐进稳定。
[0043]
相比于现有技术，本发明的有益效果在于：
[0044]
1、该新型趋近律的板球系统滑模控制方法通过分析板球系统模型，由轨迹误差，设计滑模面，根据系统数学模型得出等效控制器；设计出新型趋近律，再由等效控制器与新型趋近律设计出滑模控制器，并由lyapunov证明所设计控制器能使系统渐进稳定，符合设计要求，能够提高响应速度以及控制精度，提高了板球系统的跟踪精度，同时有效抑制了系统抖振。
附图说明
[0045]
附图用来提供对本发明的进一步理解，并且构成说明书的一部分，与本发明的实施例一起用于解释本发明，并不构成对本发明的限制。
[0046]
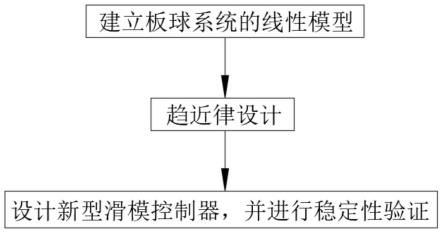
图1为本发明提出的一种新型趋近律的板球系统滑模控制方法的流程框图。
具体实施方式
[0047]
一种新型趋近律的板球系统滑模控制方法，该控制方法具体步骤如下：
[0048]
建立板球系统的线性模型：对小球位置信息进行采集，并构建板球系统的线性模型。
[0049]
具体的，首先计算机忽略小球滚动中机械结构的内部摩擦力，同时假设小球与板面未分离，且由于小球在工作点附近倾角很小，所以有sinα≈α，sinβ≈β，且其中α是平板x轴方向的倾角，β为y轴方向的倾角，同时对倾角α以及β进行进行线性化处理以生成板球系统模型，板球系统模型生成完成后，依据该模型生成小球状态空间方程，同时
由于x轴与y轴对称，其原理一致，故只分析x轴，同时生成x轴的线性模型。
[0050]
需要进一步说明的是，具体板球系统模型公式如下：
[0051][0052]
其中，mq为小球质量，rq为小球半径，iq为小球转动惯量，g为重力加速度；
[0053]
小球状态空间方程具体如下：
[0054][0055]
其中，
[0056]
此外，需要进一步说明的是，x轴的线性模型具体表示形式如下：
[0057][0058]
其中，g(x)＝-γg，d(t)为干扰项。
[0059]
趋近律设计：设计新型趋近律，同时对该趋近率进行分析。
[0060]
具体的，依据板球系统模型生成的各项数据设计相关切换函数，当系统到达滑模面时，s＝0，易知同时将公式(3)带入切换函数以获取等效控制率，同时，为保证系统快速收敛，且减小系统抖振，设计新型趋近律，对新型趋近律进行分析，当系统状态距离滑模面越远时，收敛速度越快，可保证快速收敛；当距离滑模面较近时，其收敛速度变慢，且由于幂次趋近项的存在，可保证系统平滑地进入滑模面，以达到抑制系统抖振的效果。
[0061]
需要进一步说明的是，切换函数具体计算公式如下：
[0062][0063][0064]
其具体等效控制具体计算公式如下：
[0065][0066]
其中，新型趋近律具体计算公式如下：
[0067][0068]
其中，sgn()为符号函数，k1＞0，0＜λ＜1，k＞1，μ＞1。
[0069]
设计新型滑模控制器，并进行稳定性验证：依据新型趋近律以及等效控制律构建新型滑模控制器，并对该新型滑模控制器进行滑模控制方法的稳定性验证。
[0070]
具体的，依据上述公式(6)以及公式(7)设计新型滑模控制器，同时选取lyapunov函数以对新型滑模控制器的滑模控制方法的稳定性进行验证。
[0071]
需要进一步说明的是，其新型滑模控制器具体表示形式如下：
[0072][0073]
其lyapunov函数具体计算公式如下：
[0074][0075]
由公式(9)可知v≥0；
[0076]
对公式(9)求导得：
[0077][0078]
故整个系统渐进稳定。