多个非完整移动智能体连接保持的协同控制器设计方法

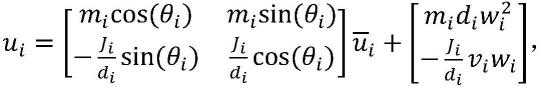
1.本发明属于控制科学技术领域，涉及一种协同控制器，尤其是涉及一种多个非完整移动智能体连接保持的协同控制器设计方法。


背景技术：

2.在通信网络满足一定连通性假设的情况下，利用分布式控制器解决多个非完整移动智能体的各种协同控制问题已经有了广泛的研究。例如，同步问题、无领导编队问题、领导者跟随者编队形成问题等。
3.在文献“cooperative output regulation with application to multi-agent consensus under switching network”(su youfeng et al.ieee transactions on systems,man,and cybernetics,part b(cybernetics),2012,42(3):864-875)中针对多个非完整移动智能体，在运动演化过程中，假设通讯图可以保持足够频繁的连接。然而，对于给定的初始状态和参数集，在实践中很难甚至不可能满足和验证这一假设。事实上，初始网络的连通性一般不能保证整个网络在长时间运动过程中的连通性，受智能体感知和通信能力的限制，智能体之间的交互拓扑结构可能会随着时间的推移而改变。因此，研究智能体的连通性保持问题具有重要的实质意义。


技术实现要素：

4.本发明的目的就是为了克服上述现有技术存在的缺陷而提供一种多个非完整移动智能体连接保持的协同控制器设计方法，实现初始保持通信的智能体能够一直保持通信，同时还能实现智能体之间的协同达到编队效果。
5.本发明的目的可以通过以下技术方案来实现：
6.一种多个非完整移动智能体连接保持的协同控制器设计方法，用于解决编队形成协同控制问题，其特征在于，包括以下步骤：
7.s1、构建多智能体系统的动力学方程，所述多智能体系统为具有n+1个智能体的多智能体系统，包括n个跟随者和1个领导者；
8.s2、获取领导者与跟随者系统的时变通讯图其中，点集是边集，并定义i的邻居节点集为：是边集，并定义i的邻居节点集为：t表示时刻；
9.s3、通过坐标变换构建与所述多智能体系统对应的闭环系统：
[0010][0011]
其中，ri是坐标转换后的位置，是新的输入，ψ(
·
)是势能函数，a
ij
(t)为边集参数；
[0012]
s4、设计分布式动态状态反馈控制器ui使得对于任意初始条件x0(0)、xi(0)、yi(0)、θi(0)、vi(0)、wi(0)，i＝1,
…
n，使连接，使得闭环系统具有以下性质：(1)对于任意t，连接；(2)并且获得的分布式动态状态反馈控制器ui表示为：
[0013][0014]
其中，θi是智能体i的角度，vi是线速度，ωi是角速度，mi是质量，ji是质量转动惯量。
[0015]
进一步地，所述跟随者的动力学方程为：
[0016][0017]
其中，对于i＝1,
…
,n，(xi,yi,)是智能体i中心的笛卡尔坐标，fi是力，τi是作用于智能体的力矩。
[0018]
进一步地，所述领导者的动力学方程基于领导者信号x0构建，所述领导者信号x0是由以下形式的线性系统生成：i2是二阶单位矩阵。
[0019]
进一步地，所述领导者的时间轨迹为：hi(t)＝[at+x
di
,ct+y
di
]，其中，a、c、x
di
和y
di
均是常数。
[0020]
进一步地，给出任意传感器有效通讯距离常数r＞0和常数∈∈[0,r)，对于任意t≥0，时变通讯图的边集足以下条件：(1)足以下条件：(1)(2)如果||ri(t)-rj(t)||≥r，那么(3)(4)对于i＝0,1,
…
,n,j＝1,
…
,n，如果并且||ri(t)-rj(t)||＜(r-∈)，那么(5)对于i＝0,1,
…
,n,j＝1,
…
,n，如果并且||ri(t)-rj(t)||＜r，那么其中，在t时刻，如果那么称||ri(t)-rj(t)||是边(i,j)的长度。
[0021]
进一步地，所述坐标转换具体为：
[0022]ri
＝q
i-d
i0
，i＝1,
…
,n
[0023][0024]
其中，qi第i个智能体轮轴的位置，d
i0
为第i个跟随者与领导者的距离，fi是力，τi是作用于智能体的力矩。
[0025]
进一步地，所述qi表示为：
[0026]
[0027]
进一步地，所述边集参数的值通过以下方式确定：
[0028]
对于i＝1,
…
,n，j＝0,1,
…
,n，如果那么a
ij
＝1，否则a
ij
＝0。
[0029]
进一步地，所述势能函数ψ(s)设计如下：0≤s＜r，其中，r是传感器有效通讯距离常数。
[0030]
本发明还提供一种电子设备，包括：
[0031]
一个或多个处理器；
[0032]
存储器；和
[0033]
被存储在存储器中的一个或多个程序，所述一个或多个程序包括用于执行如上任一所述协同控制器设计方法的指令。
[0034]
与现有技术相比，本发明具有以下有益效果：
[0035]
1、本发明将合作输出调节问题与势函数技术相结合，进一步研究了多个非完整移动智能体的领导者跟随者编队和连通性保持问题。
[0036]
2、本发明没有设置通信图满足任何连通性假设，使控制器具有保持初始连接网络的连通性的能力，同时在领导者沿直线移动时，实现移动智能体群的领导者跟随者编队形成。本发明要求初始通信图为连接图而不是假设通讯图可以保持足够频繁的连接，实现初始保持通信的智能体能够一直保持通信，同时还能实现智能体之间的协同达到编队效果。
[0037]
3、本发明的控制算法能够使通信距离有限的智能体最终达到协同的控制目标。
[0038]
4、本发明适用于一些智能体传感器有效通讯距离有限的编队任务，具有良好的实际应用价值。
附图说明
[0039]
图1为本发明控制器设计流程示意图；
[0040]
图2为本发明多个非完整移动机器人的预期编队情况示意图；
[0041]
图3为多个非完整移动机器人初始连接拓扑图边的长度变化图；
[0042]
图4为跟随者与领导者之间的距离变化图；
[0043]
图5为不同时刻的编队情况图。
具体实施方式
[0044]
下面结合附图和具体实施例对本发明进行详细说明。本实施例以本发明技术方案为前提进行实施，给出了详细的实施方式和具体的操作过程，但本发明的保护范围不限于下述的实施例。
[0045]
本发明提供一种多个非完整移动智能体连接保持的协同控制器设计方法，在没有设置通信图满足任何连通性假设情况下，解决能够使得通讯图连接保持的编队形成协同控制问题，为移动智能体群的领导者跟随者编队形成控制提供重要技术支撑。
[0046]
如图1所示，该协同控制器设计方法包括以下步骤：
[0047]
步骤s1，构建多智能体系统，该多智能体系统为具有n+1个智能体的多智能体系统，包括n个跟随者和1个领导者，获取该多智能体系统的动力学方程。
[0048]
(1)跟随者的动力学方程
[0049]
本实施例中，构建以下形式的跟随者的系统运动学方程：本实施例中，构建以下形式的跟随者的系统运动学方程：其中，对于i＝1,
…
,n，(xi,yi)是智能体中心的笛卡尔坐标，θi是角度，vi是线速度，ωi是角速度，mi是质量，ji是质量转动惯量，fi是力，τi是作用于智能体的力矩。
[0050]
(2)领导者的动力学方程
[0051]
本实施例中，定义领导者的时间轨迹为hd(t)＝[at+x
d0
,ct+y
d0
]，其中a为某常数，c为某常数，x
d0
为某常数，y
d0
为某常数。因此，给出领导者信号x0是由以下形式的线性系统生成：其中i2是二阶单位矩阵，通过选择初始条件x0(0)＝[x
d0
,y
d0
,a,c]，可以得出
[0052]
步骤s2，获取领导者与跟随者系统的时变通讯图。
[0053]
在多智能体系统中，一般地，由于领导者与跟随者之间的通讯障碍，第i个智能体的控制输入ui不能访问其余全部节点的信息。为了更直观地描述通讯障碍，定义时变通讯图如下：其中点集节点0与领导者系统相关，节点i，i＝1,
…
,n与跟随者系统中第i个智能体(即第i个跟随者)相关，是边集。边集定义如下：对于i＝1,
…
,n，j＝0,1,
…
,n，i≠j，当且仅当在t时刻第i个智能体的控制输入ui能访问第j个智能体的信息，才会有定义智能体i的邻居节点集为：
[0054]
本实施例中，采用分布式状态反馈方法使得跟随者能够沿着某条直线hi(t)＝[at+x
di
,ct+y
di
]移动并形成一个几何分布图，如图2所示，即提出编队形成问题，其中x
di
和y
di
是常数。
[0055]
步骤s3，对跟随者的动力学方程进行坐标转换，形成双积分器多智能体系统。
[0056]
为了定义通讯图的边，让qi以距离di表示第i个移动智能体轮轴的位置：应用到步骤s1中形成以下坐标转换：
[0057]ri
＝q
i-d
i0
,i＝1,
…
,n
[0058][0059]
从而得出以下双积分器跟随者系统：pi为中间参数。其中，ri是转换后的位置，是新的输入。同时，令r0(t)＝h
d0
(t)，那么
[0060]
该双积分器跟随者系统与领域者动力学方程共同形成双积分器多智能体系统。
[0061]
步骤s4，定义时变通讯图的边集满足条件。
[0062]
给出任意传感器有效通讯距离常数r＞0和常数∈∈[0,r)，对于任意t≥0，被定义为满足以下条件：(1)被定义为满足以下条件：(1)(2)如果||ri(t)-rj(t)||≥r，那么(3)对于i＝0,1,
…
,n；(4)对于i＝0,1,
…
,n,j＝1,
…
,n，如果并且||ri(t)-rj(t)||＜(r-∈),那么(5)对于i＝0,1,
…
,n,j＝1,
…
,n，如果并且||ri(t)-rj(t)||＜r,那么在t时刻，如果那么称||ri(t)-rj(t)||是边(i,j)的长度。
[0063]
步骤s5，针对步骤s3的双积分器多智能体系统设计分布式状态反馈控制器。
[0064]
分布式动态状态反馈控制器的一般形式设计为：分布式动态状态反馈控制器的一般形式设计为：其中，设计设计hi是充分光滑的函数。
[0065]
所设计的分布式状态反馈控制器具体形式为：所设计的分布式状态反馈控制器具体形式为：其中，对于i＝1,
…
,n，j＝0,1,
…
,n，如果那么a
ij
＝1，否则a
ij
＝0。生成如下的闭环系统：＝0。生成如下的闭环系统：
[0066]
本实施例中，为了处理连接性保持问题，势能函数ψ(s)设计如下：从而可以得出ψ(s)的微分形式为
[0067]
步骤s6，针对原有的多智能体系统编队形成问题设计控制器。
[0068]
提出能够使得通讯图连接保持的编队形成协同控制问题。对于步骤s1中的多智能体系统，r＞0，∈∈[0,r)，设计分布式控制器使得对于任意初始条件x0(0)、xi(0)、yi(0)、θi(0)、vi(0)、wi(0)，i＝1,
…
n，使连接，使得闭环系统具有以下性质：(1)对于任意，连接；(2)并且
[0069]
对于步骤s1中的多智能体系统编队形成问题，分布式动态状态反馈控制器被具体设计为：其中在步骤s5中给出。
[0070]
步骤s7，仿真验证。
[0071]
本实施例中，步骤s1中的原有的多智能体的系统参数为：mi＝1，ji＝1，di＝1，i＝1,
…
,4。假设传感距离r＝8，∈＝0.5。控制目标是找到分布式控制输入ui使得当d
10
＝[-2,
2]、d
20
＝[-2,-2]、d
30
＝[-4,-4]和d
40
＝[-4,4]时，4,4]时，各个变量的初值设为：(x1(0),y1(0))＝[4 4]
t
、(x2(0),y2(0))＝[10 0]
t
、(x3(0),y3(0))＝[2 0]
t
、(x4(0),y4(0))＝[0 8]
t
、θ1(0)＝1、θ2(0)＝0、θ3(0)＝1、θ4(0)＝0、(v1(0),w1(0))＝[7 2]
t
、(v2(0),w2(0))＝[0 0]
t
、(v3(0),w3(0))＝[0
ꢀ‑
1]
t
、(v4(0),w4(0))＝[0 0]
t
和x0(0)＝[8 0 1 1]
t
。可以得出这些初值能够使得形成一个连接的通讯图。经过步骤s6设计的控制器，仿真效果如图3-图5所示。图3展示了边{(0,1),(1,4),(0,2),(1,3)}在t≥0的长度，可以看出，都小于传感器距离8，因此，通讯图连接保持。图4展示了4个跟随者到领导者d
i0
的距离。图5展示了5个多智能体分别在t＝0s,20s,50s,100s的编队位置。由图3-图5的仿真结果可以看出，步骤s6中的分布式动态状态反馈控制器能够解决所提出的能够使得通讯图连接保持的编队形成协同控制问题。
[0072]
上述方法如果以软件功能单元的形式实现并作为独立的产品销售或使用时，可以存储在一个计算机可读取存储介质中。基于这样的理解，本发明的技术方案本质上或者说对现有技术做出贡献的部分或者该技术方案的部分可以以软件产品的形式体现出来，该计算机软件产品存储在一个存储介质中，包括若干指令用以使得一台计算机设备(可以是个人计算机，服务器，或者网络设备等)执行本发明各个实施例所述方法的全部或部分步骤。而前述的存储介质包括：u盘、移动硬盘、只读存储器(rom，read-only memory)、随机存取存储器(ram，random access memory)、磁碟或者光盘等各种可以存储程序代码的介质。
[0073]
以上详细描述了本发明的较佳具体实施例。应当理解，本领域的普通技术人员无需创造性劳动就可以根据本发明的构思作出诸多修改和变化。因此，凡本技术领域中技术人员依本发明的构思在现有技术的基础上通过逻辑分析、推理或者有限的实验可以得到的技术方案，皆应在由权利要求书所确定的保护范围内。