融合神经网络的改进HHO算法AGV路径规划

融合神经网络的改进hho算法agv路径规划
技术领域
1.本发明涉及一种agv路径规划领域，具体为融合神经网络的改进hho算法agv路径规划。


背景技术：

2.a*算法是由国外专家p.e.hart提出的概念，是静态路径规划中较为有效的求解路径搜索问题的方法，并被应用于智能引导车、gps导航系统等领域。该方法主要思想为：以agv搬运任务起始点为中心，以周围所有可行走栅格为目标点，向外围区域逐步扩展，直到扩展对象为目标点时，完成算法运行。a*算法以其搜索范围广、多指标评价路径等优点被广泛应用。但对于研究车间系统路径规划问题效果并不明显，a*算法在过程中需要将环境分解为大量的栅格节点作为公式计算的数据集，对于车间agv运行环境而言这种分解方法过于繁杂，这个过程在算法运算中会消耗大量时间，并且不能完全保证搜索到最优的路径，一旦车间环境发生改变，所有的数据集将需要被重新定义，这为优化问题带来了巨大的麻烦。而对于agv运行而言，不能对agv运行角度进行控制，这在实际生产中也会为具体路径的铺设造成困难。
3.目前备受研究者关注的智能算法是哈里斯鹰优化算法(hho)，具有参数少、精度高的特点。国内外众多学者使用该算法很好地解决了一些实际问题。essam等使用哈里斯鹰算法进行药物优化设计。aneesh等人基于hho引入自适应机制研究了图像阈值分割问题。传统的哈里斯鹰算法并非完美，结构本身存在一定缺陷，也即大多数生物启发式算法都有的收敛至局部极值点问题。


技术实现要素：

4.本发明的目的在于提供融合神经网络的改进hho算法agv路径规划，以解决上述背景技术中提出的问题。
5.本发明的目的是通过下述技术方案予以实现：融合神经网络的改进hho算法agv路径规划，由如下步骤组成：
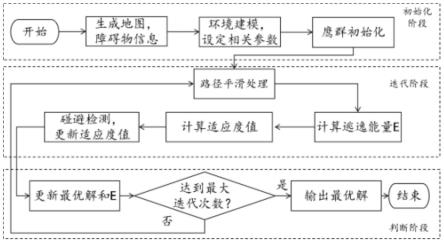
6.(1)第一步：初始化阶段，初始化阶段先生成障碍物地图，设定好算法相关参数后对哈里斯鹰个体进行位置初始化，并得到初步路径；
7.(2)第二步：迭代阶段，迭代阶段先对路径作平滑处理，计算逃逸能量和路径的适应度值，将路径对所有障碍物进行碰撞检测，判断是否与障碍物现在相撞；
8.(3)第三步：判断阶段，判断阶段主要就根据迭代结果更新个体位置和逃逸能量，直至达到最大次数输出最优路径；
9.在本发明一个较佳的实施例中，所述路径平滑处理采用贝塞尔曲线，贝塞尔曲线可将尖锐拐点消除，使之更适宜agv现实使用。
10.在本发明一个较佳的实施例中，所述环境建模以可视图法建模，可视图法使用凸多边形拟合映射的障碍物信息，进而将路径规划问题简化为约束条件下求最短路线问题。
11.在本发明一个较佳的实施例中，所述在hho算法中，猎物能量e的大小起着调节和过渡随机探测和局部围攻的重要作用，|e|《1且越小时，算法则执行局部围攻；|e|≥1且越大时，算法则进行随机探测；传统hho的能量方程e从初始值e0线性递减至0，这一变化过程不利于脱离局部极值的收敛；因此以动态能量平衡全局和局部搜索，首先借鉴双曲正切函数的思想，在算法迭代前中期位置更新处引入动态双曲正切速率s，迭代后期引入正弦波动速率；其中采用的动态双曲正切速率，在算法迭代前期，改进算法获得较大猎物能量以保证其在更广阔的区域搜索最优解；在算法迭代中期，改进算法获得较小猎物能量，使当前个体可以在最优个体附进行精确搜索，有效地平衡了全局探测与局部寻优；算法迭代后期，利用正弦波不规则变换的特点来增强最优个体在局部空间开发的多元性，协助哈里斯鹰个体跳出局部最优。
12.本发明的有益效果是：该融合神经网络的改进hho算法agv路径规划，改进的hho算法比hho算法收敛速度更快，得到更短更平滑的路径。
附图说明
13.图1是本发明系统图；
14.图2是本发明动态能量变化曲线图；
15.图3是本发明环境模型图；
16.图4是本发明静态环境规划路径对比图；
17.图5是本发明动态环境规划路径图；
具体实施方式
18.下面结合具体实施方式进一步的说明，但是下文中的具体实施方式不应当做被理解为对本体发明的限制。本领域普通技术人员能够在本发明基础上显而易见地作出的各种改变和变化，应该均在发明的范围之内。
19.如图1，本发明的实施例包括：
20.融合神经网络的改进hho算法agv路径规划，由如下步骤组成：
21.(1)第一步：初始化阶段，初始化阶段先生成障碍物地图，设定好算法相关参数后对哈里斯鹰个体进行位置初始化，并得到初步路径；
22.(2)第二步：迭代阶段，迭代阶段先对路径作平滑处理，计算逃逸能量和路径的适应度值，将路径对所有障碍物进行碰撞检测，判断是否与障碍物现在相撞；
23.(3)第三步：判断阶段，判断阶段主要就根据迭代结果更新个体位置和逃逸能量，直至达到最大次数输出最优路径；
24.值得一提的是，所述路径平滑处理采用贝塞尔曲线，贝塞尔曲线可将尖锐拐点消除，使之更适宜agv现实使用，所述环境建模以可视图法建模，可视图法使用凸多边形拟合映射的障碍物信息，进而将路径规划问题简化为约束条件下求最短路线问题，所述在hho算法中，猎物能量e的大小起着调节和过渡随机探测和局部围攻的重要作用，|e|《1且越小时，算法则执行局部围攻；|e|≥1且越大时，算法则进行随机探测；传统hho的能量方程e从初始值e0线性递减至0，这一变化过程不利于脱离局部极值的收敛；因此以动态能量平衡全局和局部搜索，首先借鉴双曲正切函数的思想，在算法迭代前中期位置更新处引入动态双曲正
切速率s，迭代后期引入正弦波动速率；其中采用的动态双曲正切速率，在算法迭代前期，改进算法获得较大猎物能量以保证其在更广阔的区域搜索最优解；在算法迭代中期，改进算法获得较小猎物能量，使当前个体可以在最优个体附进行精确搜索，有效地平衡了全局探测与局部寻优；算法迭代后期，利用正弦波不规则变换的特点来增强最优个体在局部空间开发的多元性，协助哈里斯鹰个体跳出局部最优。
25.具体实施方式，改进的哈里斯鹰优化算法，(1)动态能量策略，在hho算法中，猎物能量e的大小起着调节和过渡随机探测和局部围攻的重要作用，|e|《1且越小时，算法则执行局部围攻；|e|≥1且越大时，算法则进行随机探测；传统hho的能量方程e从初始值e0线性递减至0，这一变化过程不利于脱离局部极值的收敛；因此以动态能量平衡全局和局部搜索，首先借鉴双曲正切函数的思想，在算法迭代前中期位置更新处引入动态双曲正切速率s，迭代后期引入正弦波动速率；其中采用的动态双曲正切速率，在算法迭代前期，改进算法获得较大猎物能量以保证其在更广阔的区域搜索最优解；在算法迭代中期，改进算法获得较小猎物能量，使当前个体可以在最优个体附进行精确搜索，有效地平衡了全局探测与局部寻优；算法迭代后期，利用正弦波不规则变换的特点来增强最优个体在局部空间开发的多元性，协助哈里斯鹰个体跳出局部最优；
[0026][0027]
式中，s0表示初始速度，当迭代次数t＝0时s0＝3，send＝0.4表示迭代结束时的速度，即迭代次数达到最大值tmax；经过多次实验，利用调节因子控制曲线的平滑度，最终使用，μ1＝0.23，μ2＝0.06，μ3＝1.6，θ＝0.3，进行仿真时结果最优；
[0028]
(2)曲线平滑与计算，贝塞尔曲线是一种常用的矢量绘制曲线，可将二维平面中若干任意点绘制成光滑的曲线，引入贝塞尔曲线可将尖锐拐点消除，使之更适宜agv现实使用；
[0029]
n次贝塞尔曲线表达式如下：
[0030][0031]
式中，p(s)为控制点，s为变量，p(i)代表位置点，其中b
i,n
(s)为n次伯恩斯坦多项式，可表示为：
[0032][0033]
式中，位置点个数为n+1，控制点个数为n-1；
[0034]
贝塞尔曲线的一阶导数公式如下：
[0035][0036]
平滑后的曲线长度还需计算适应度值，对平滑路径进行h等分，以路径长度fi为适应度值，则适应度函数如下所示：
[0037]
[0038]
式中||h
i,k+1-h
i,k
||为终点h
i,k+1
和起点h
i,k
之间的距离；
[0039]
(3)仿真及分析，环境建模，本发明以可视图法建模，可视图法使用凸多边形拟合映射的障碍物信息，进而将路径规划问题简化为约束条件下求最短路线问题；图3为agv路径规划的环境模型；模型中，障碍物映射成形状各异的多边形，将起点s至终点t连线所在射线为横轴，过起点的垂线为纵轴，建立一个局部坐标系s-x'y'，用d条虚拟坐标横轴的垂线l1～ld将路径平分d+1段，在垂直线li(i＝1,2,
…
,d)上随机选一无碰撞节点pi，最后将各点连线得到完整路径p
patp
＝{p
1-s,
…
,p
d-p
d-1
,t-pd}；再通过公式将无碰撞节点转化成全局坐标系坐标，转换方程如下所示：
[0040][0041]
式中(xs,y
x
)为全局坐标系中s起点的坐标，各路径点的x坐标可由公式在局部坐标系中求得；θ是全局坐标系x轴逆时针旋转至平行于局部坐标系x'的角度；
[0042]
(4)参数设置，为验证改进后算法在agv路径规划问题中的是否具备优越性，以matlab r2016a软件为基础，将算法思路进行仿真；算法的参数设置为：种群数量n＝100；最大迭代次数tmax＝200；猎物初始逃离能量e0＝3，仿真环境范为100m
×
100m；
[0043]
(5)静态地图仿真，设置障碍较少和障碍较多两种不同的静态环境进行仿真对比；图4给出较少障碍和较多障碍环境下传统hho算法与改进hho算法路径规划对比；
[0044]
(6)动态地图仿真，在地图坐标为(95，20)和(60，95)分别设置动态障碍物，圆形障碍物以agv同等速度沿x轴负方向运动至接触y轴，矩形障碍物以agv同等速度沿y轴负方向运动至接触x轴；重复30次取最优结果路径，如图5所示；
[0045]
(7)结果分析，将仿真结果归纳至表1所示；
[0046]
表1指标对比
[0047][0048]
仿真结果表明，在静态较少障碍环境下，改进hho比传统hho算法最优路径减少18.41m，缩短了11.87％，最优迭代次数减少26次约14.61％；在静态较多障碍环境下，改进hho比传统hho算法最优路径减少58.97m，缩短了33.86％，最优迭代次数减少30次约16.22％；在动态障碍环境下，改进hho规划出最优路径为115.26，稳定迭代次数为165次，由于传统hho算法未融合神经网络与障碍避碰检测，在动态环境失败率极高，在此不作比较；综合来看，改进hho算法比hho算法收敛速度更快，得到更短更平滑的路径。
[0049]
以上描述仅为本技术的较佳实施例以及对所运用技术原理的说明。本领域技术人
员应当理解，本技术中所涉及的发明范围，并不限于上述技术特征的特定组合而成的技术方案，同时也应涵盖在不脱离所述发明构思的情况下，由上述技术特征或其等同特征进行任意组合而形成的其它技术方案。例如上述特征与本技术中公开的(但不限于)具有类似功能的技术特征进行互相替换而形成的技术方案。