一种基于增广LQR的矿车横向控制方法与流程

一种基于增广lqr的矿车横向控制方法
技术领域
1.本发明涉及矿车自动驾驶技术领域，特别涉及一种基于增广lqr的矿车横向控制方法。


背景技术：

2.面对日益增长的采矿需求，各大矿企一方面在增加运输设备的数量和单车运能，另一方面增加作业时长，但是长时间工作在矿山折衷恶劣环境下对工人的身体是一大挑战，并且很多运输设备非常高大，存在较大视野盲区，很容易出安全事故。基于上述各种原因，矿山自动驾驶是解决上述问题的一个可行手段。
3.目前，针对乘用车的自动驾驶算法相对成熟，矿车的自动驾驶算法正在不断完善中。矿车的自动驾驶的一大难关是对矿车的精确控制，因为矿车存在比较大的执行器响应延迟，这缘于矿车本身巨大的自重和载重。矿车工作在曲率不断变化的矿山道路中，控制精度的高低直接影响矿车自动驾驶最终是否能够批量运行。
4.现有技术的不足之处，目前的矿车本身宽度较大，道路宽度有限，稍大的横向误差就有可能导致辆车碰撞或掉入碰触道路两侧基础设施。现有的基于lqr的控制方法，未将执行器响应延迟特性直接以状态变量的形式考虑在状态空间表达中，往往需要通过增加超前环节等手段解决控制响应延迟的问题，但该手段只能从系统外部解决问题，控制效果有限。


技术实现要素：

5.本发明的目的克服现有技术存在的不足，为实现以上目的，采用一种基于增广lqr的矿车横向控制方法，以解决上述背景技术中提出的问题。
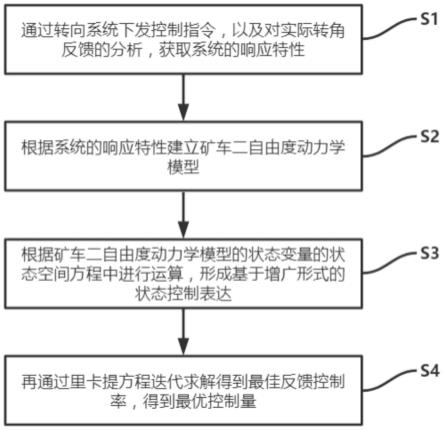
6.一种基于增广lqr的矿车横向控制方法，具体步骤包括：
7.通过转向系统下发控制指令，以及对实际转角反馈的分析，获取系统的响应特性；
8.根据系统的响应特性建立矿车二自由度动力学模型；
9.根据矿车二自由度动力学模型的状态变量的状态空间方程中进行运算，形成基于增广形式的状态控制表达；
10.再通过里卡提方程迭代求解得到最佳反馈控制率，得到最优控制量。
11.作为本发明的进一步的方案：所述建立矿车二自由度动力学模型的具体步骤包括：
12.基于数学模型将矿车车辆的动力学特性和系统的响应特性进行表达；
13.定义状态变量为其中e1,e2分别表示横向偏移和航向角偏差，得到状态空间方程为：
[0014][0015]
其中，σ1＝2(c
αf
+c
αr
),σ2＝-2(l
fcαf-l
rcαr
),c
αf
,c
αr
,v
x
,m,iz,lf,lr分别表示矿车前轮侧偏刚度、后轮侧偏刚度、车辆纵向车速、矿车质量、矿车横摆转动惯量、矿车质心到前轴距离，以及矿车质心到后轴距离，cr为道路前视点的曲率。
[0016]
作为本发明的进一步的方案：所述根据矿车二自由度动力学模型的状态变量的状态空间方程中进行运算，形成基于增广形式的状态控制表达的具体步骤包括：
[0017]
根据矿车二自由度动力学模型的状态空间方程，在状态变量中引入实时转角反馈即将状态空间增广为并根据对转向系统的分析，得到表达式：
[0018][0019]
联立状态空间方程，得到：
[0020][0021]
再将上述状态空间方程按照固定时间步长δt转化为离散系统，得到：
[0022]
x(k+1)＝ax(k)+bδ(k)+dcr(k)；
[0023]
其中，a,b,d分别为系统的系数矩阵，k表示步数。
[0024]
同时根据上述公式，得到代价函数：
[0025][0026]
s.t.x(k+1)＝ax(k)+bδ(k)
[0027]
其中，q，r分别为正定的权重矩阵，τ表示转向系统的响应延迟时间。
[0028]
作为本发明的进一步的方案：所述通过里卡提方程迭代求解得到最佳反馈控制率，得到最优控制量的具体步骤包括：
[0029]
首先基于增广lqr求解矿车二自由度动力学模型，得到最优状态反馈控制增益矩阵k；
[0030]
再采用里卡提方程迭代求解；
[0031]
令p＝q，当err》tolerance，且iteration_num《max_ineration_num时；
[0032]
迭代执行：
[0033]
如果iteration_num《max_ineration_num，令k＝-(r+b
t
pb)-1bt
pa；
[0034]
由于控制量δ＝-kx，需要考虑道路曲率影响，引入前馈量；
[0035]
所述引入的前馈量的表达为：
[0036][0037]
其中，l为轴距，
[0038]
得到总的转角控制量为：δ＝-kx+δf。
[0039]
与现有技术相比，本发明存在以下技术效果：
[0040]
采用上述的技术方案，通过对转向系统下发控制指令，以及对实际转角反馈的分析，采用系统辨识的方法，获得该系统的响应特性；建立矿车二自由度动力学模型，并将其中四个状态变量的状态空间方程中予以考虑，形成了增广形式的状态控制表达，通过里卡提方程迭代求解得到最佳反馈控制率，得到最优控制量，省略了通过外部补偿手段解决执行器响应延迟的过程，节省了相关参数标定的工作，并且能够保证控制量最优。
附图说明
[0041]
下面结合附图，对本发明的具体实施方式进行详细描述：
[0042]
图1为本技术公开的一些实施例的矿车横向控制方法的步骤示意图；
[0043]
图2为本技术公开的一些实施例的矿车二自由度模型的示意图；
[0044]
图3为本技术公开的一些实施例的矿车横向控制方法的流程框图。
具体实施方式
[0045]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0046]
请参考图1，本发明实施例中，一种基于增广lqr的矿车横向控制方法，具体步骤包括：
[0047]
s1、通过转向系统下发控制指令，以及对实际转角反馈的分析，获取系统的响应特性；
[0048]
s2、根据系统的响应特性建立矿车二自由度动力学模型；
[0049]
建立矿车二自由度模型的目的是为了以数学方式对车辆的动力学特性进行表达，将车辆的表现与施加的控制量以数学形式进行表达；
[0050]
如图2所示，图示为矿车二自由度模型的示意图；
[0051]
具体实施例中，建立矿车二自由度模型具体步骤包括：
[0052]
基于数学模型将矿车车辆的动力学特性和系统的响应特性进行表达；
[0053]
定义状态变量为其中e1,e2分别表示横向偏移和航向角偏差，得到状态空间方程为：
[0054][0055]
其中，σ1＝2(c
αf
+c
αr
),σ2＝-2(l
fcαf-l
rcαr
),c
αf
,c
αr
,v
x
,m,iz,lf,lr分别表示矿车前轮侧偏刚度、后轮侧偏刚度、车辆纵向车速、矿车质量、矿车横摆转动惯量、矿车质心到前轴距离，以及矿车质心到后轴距离，cr为道路前视点的曲率。
[0056]
具体实施方式中，由于矿车车辆的执行器是存在延迟的，通过对液压转向系统的响应特性进行分析，发现下发的转向角度与实际的转角响应存在一个类似于一阶延时的环节，故而在实际的转角响应与下发的转角响应之间以一阶延迟环节来表示。
[0057]
s3、根据矿车二自由度动力学模型的状态变量的状态空间方程中进行运算，形成基于增广形式的状态控制表达，具体步骤包括：
[0058]
根据矿车二自由度动力学模型的状态空间方程，在状态变量中引入实时转角反馈δ表示转角指令，即将状态空间增广为并根据对转向系统的分析，得到表达式：
[0059][0060]
联立状态空间方程，得到：
[0061][0062]
再将上述状态空间方程按照固定时间步长δt转化为离散系统，得到：
[0063]
x(k+1)＝ax(k)+bδ(k)+dcr(k)；
[0064]
其中，a,b,d分别为系统的系数矩阵，k表示步数。
[0065]
同时根据上述公式，得到代价函数：
[0066][0067]
s.t.x(k+1)＝ax(k)+bδ(k)
[0068]
其中，q，r分别为正定的权重矩阵，τ表示转向系统的响应延迟时间。
[0069]
s4、再通过里卡提方程迭代求解得到最佳反馈控制率，得到最优控制量，具体步骤包括：
[0070]
如图3所示，图示为方案求解的流程图；
[0071]
首先基于增广lqr求解矿车二自由度动力学模型，得到最优状态反馈控制增益矩阵k；
[0072]
再采用里卡提方程迭代求解，具体步骤如下：
[0073]
令p＝q，当err》tolerance，且iteration_num《max_ineration_num时；
[0074]
迭代执行：
[0075]
如果iteration_num《max_ineration_num，令k＝-(r+b
t
pb)-1bt
pa，求解结束；
[0076]
由于控制量δ＝-kx，且上述求解未考虑道路曲率影响，为此还需要引入前馈，以消除道路曲率对控制带来的无法收敛的问题，引入前馈量；
[0077]
所述引入的前馈量的表达为：
[0078][0079]
其中，l为轴距，
[0080]
得到总的转角控制量为：δ＝-kx+δf。
[0081]
尽管已经示出和描述了本发明的实施例，对于本领域的普通技术人员而言，可以理解在不脱离本发明的原理和精神的情况下可以对这些实施例进行多种变化、修改、替换和变型，本发明的范围由所附权利要求及其等同物限定，均应包含在本发明的保护范围之内。