一种磁悬浮转子奇次谐波振动力抑制方法

1.本发明涉及磁悬浮转子奇次谐波振动力抑制的技术领域，具体涉及一种磁悬浮转子奇次谐波振动力抑制方法，基于粒子群参数优化二阶双模奇次重复控制器实现，用于对磁悬浮控制力矩陀螺转子系统中奇次谐波振动力进行抑制，为磁悬浮控制力矩陀螺在“超静”、“超稳”卫星平台上的超敏捷动中成像应用提供技术支持。


背景技术：

2.控制力矩陀螺以其输出力矩大、控制精度高、动态响应快的优点，成为了敏捷机动卫星理想的姿态控制执行机构。相比于传统的机械轴承控制力矩陀螺，磁悬浮控制力矩陀螺(mscmg)采用主动磁轴承实现转子的无接触悬浮，从根源上解决了机械轴承的摩损问题，具有无摩擦、无需润滑、低噪声、大转速、长寿命的突出特点，且可通过设计算法实现主动振动控制。因此mscmg是空间应用技术中具有卓越发展潜能的惯性执行机构。
3.磁悬浮转子系统的主要振动源为转子几何轴和惯性轴不重合产生的质量不平衡和闭环控制系统中位移传感器引入的传感器谐波。这些振动源是材料不均匀以及加工装配误差引起的，在实际工程中是不可避免的。质量不平衡包括静不平衡和动不平衡，静不平衡产生与转子转速同频的振动力；传感器谐波产生与转子转速同频和倍频的谐波振动力。磁悬浮转子产生的谐波振动力通过基座传递到航天器平台，会严重影响载荷性能，造成超敏捷机动卫星成像质量的下降，甚至会破坏系统的稳定性，导致航天器部件的损坏。因此抑制磁悬浮转子系统的谐波振动力是磁轴承控制领域中一项亟待解决的关键性技术。
4.当前磁悬浮转子系统动力学模型都是基于磁轴承力线性化的条件建立的。线性化磁轴承力包含电流刚度力和位移刚度力两部分，其中电流刚度力占磁轴承振动力的主要部分，因此抑制磁轴承线圈电流中的谐波分量可以消除大部分振动力。而磁悬浮转子系统线圈电流的主导谐波分量为奇次谐波分量，因此针对奇次谐波电流进行抑制十分必要。
5.常用于磁悬浮转子系统的谐波振动抑制方法有陷波滤波器、重复控制、多谐振控制、lms算法等。重复控制基于内模原理，可同时实现多频扰动的抑制。然而传统重复控制器存在频率波动灵敏度高、占用内存较大、动态响应速度较慢的缺点，限制了算法的抑制效果。而针对传统重复控制器的结构进行改进设计的高阶重复控制器会在系统中引入较多的控制参数，如何选取最优参数以实现系统性能要求的进一步提升具有重要研究意义。


技术实现要素：

6.本发明的技术解决问题：克服现有技术的不足，提供一种磁悬浮转子谐波振动力抑制方法，采用二阶双模奇次重复控制器实现奇次谐波振动力的抑制，并根据提出的闭环系统稳定性判据，利用粒子群算法对重复控制器的控制增益和权重因子进行离线参数优化，这不仅能提高系统频率波动鲁棒性，减少延迟时间和占用的内存，加快瞬态响应速度，提高谐波抑制精度，还能根据性能指标的要求，智能化选取更为合适的控制参数。
7.本发明采用的技术方案为：一种磁悬浮转子奇次谐波振动力抑制方法，其特征在
于：基于粒子群参数优化二阶双模奇次重复控制器实现，包括以下步骤：
8.步骤1：建立包含质量不平衡和传感器谐波的磁悬浮转子动力学模型，如下：
[0009][0010]
所建立的磁悬浮转子动力学模型等号左侧表示磁悬浮转子产生的磁轴承力，等号右侧表示磁悬浮转子在质量不平衡和传感器谐波两个扰动源的作用下产生包含谐波分量的磁轴承振动力，式中，m为转子的质量；xi和yi分别为转子在x轴、y轴方向的平动位移；δq
x
和δqy分别为转子在x轴、y轴方向的静不平衡分量；q
srx
和q
sry
分别为转子在x轴、y轴方向的传感器谐波分量；gc(s)为磁轴承控制器的传递函数；gw(s)为功率放大器的传递函数；ks为位移传感器的增益系数；ki和kh分别为电流刚度和位移刚度；s为拉普拉斯算子；
·
(s)为对应物理量的拉普拉斯变换表达式；
[0011]
步骤2：基于步骤1中的磁悬浮转子动力学模型，设计基于二阶双模奇次重复控制器，实现磁悬浮转子奇次谐波振动力抑制；
[0012]
设计二阶双模奇次重复控制器，在二阶双模奇次重复控制器中引入提高频率波动鲁棒性的权重因子w，以及调节响应速度和稳态精度的控制增益k1、k2；以谐波电流作为基于二阶双模奇次重复控制器的输入，使二阶双模奇次重复控制器在奇次谐波频率点处产生无穷增益，并将基于二阶双模奇次重复控制器的输出反馈至磁悬浮转子系统的功率放大器输入端，实现奇次谐波振动力的有效抑制；同时针对加入二阶双模奇次重复控制器的磁悬浮转子系统，提出一个新的稳定性判据，根据稳定性判据设计相位补偿环节并选取恰当的权重因子和控制增益，在保证加入基于二阶双模奇次重复控制器后闭环系统稳定性的同时，兼顾闭环系统的频率波动鲁棒性和动态特性；
[0013]
步骤3：采用粒子群算法对二阶双模奇次重复控制器的参数进行离线优化
[0014]
基于步骤2中的稳定性判据，确立了二阶双模奇次重复控制器中权重因子w和控制增益k1、k2三个参数的取值范围，建立基于二阶双模奇次重复控制器的磁悬浮转子系统仿真模型，将参数w、k1、k2作为粒子群内一个粒子的三个维度，选择时间乘绝对误差积分(itae)准则作为适应度函数，通过粒子群算法智能化选取权重因子和控制增益的最优参数值；在二阶双模奇次重复控制器中使用粒子群算法优化后的参数值，完成磁悬浮转子奇次谐波振动力抑制。
[0015]
所述步骤2中，设计的二阶双模奇次重复控制器的传递函数为：
[0016][0017]
式中，为二阶双模奇次重复控制器的内模传递函数；k1、k2分别为二阶双模奇次重复控制器两个通道的控制增益；w为权重因子；n为延迟单元数，等于采样频率和转子转频的比值；q(z)为提高系统稳定性的低通滤波器，截止频率为ωc；c(z)为使闭环系统满足稳定性判据的相位补偿函数；l(z)＝z
l
为具有一
固定超前角θ
l
(ω)＝lωts的线性相位超前补偿函数；
·
(z)为对应物理量的z变换表达式；
[0018]
所述步骤2中，加入二阶双模奇次重复控制器后磁悬浮转子系统的稳定性判据表述为：
[0019]
令控制增益k1＝k2＝k
rc
，若满足下列条件，则加入二阶双模奇次重复控制器后的磁悬浮转子系统是渐近稳定的：
[0020]
条件1：原始的磁悬浮转子系统是渐进稳定的；
[0021]
条件2：加入二阶双模奇次重复控制器后磁悬浮转子系统的控制增益k
rc
、权重因子w和相位λ(ω)满足下式：
[0022][0023]
式中，ω为角频率；λ(ω)＝θc(ω)+θf(ω)+θ
l
(ω)，θc(ω)为相位补偿函数c(z)的相频响应，θf(ω)为系统函数f(z)的相频响应，θ
l
(ω)为线性相位超前补偿函数l(z)的相频响应；m(ω)＝ac(ω)af(ω)，ac(ω)为相位补偿函数c(z)的辐频响应，af(ω)为系统函数f(z)的辐频响应；磁悬浮转子系统的系统函数f(z)为：
[0024][0025]
其中，gc(z)为磁轴承控制器的传递函数；gw(z)为功率放大器的传递函数；ks为位移传感器的增益系数；g
p
(z)为磁悬浮转子的传递函数；
[0026]
根据稳定性判据合理设计相位补偿函数c(z)以及线性相位超前补偿函数l(z)的超前拍数l，并选择合适的控制增益k
rc
、权重因子w，保证加入二阶双模奇次重复控制器后磁悬浮转子系统的稳定性。
[0027]
所述步骤3中，采用粒子群算法对二阶双模奇次重复控制器的参数进行离线优化的步骤为：
[0028]
(1)建立基于二阶双模奇次重复控制器的磁悬浮转子系统仿真模型，选择时间乘绝对误差积分(itae)准则作为适应度函数，itae准则表示为：
[0029][0030]
式中，j为适应度函数值；e(t)为线圈电流实际值和参考值之间的偏差量；t为时间；
[0031]
(2)将二阶双模奇次重复控制器的参数w、k1、k2作为粒子群算法的位置参数，初始化粒子群的规模n、维度数d、最大迭代次数、最小适应度值、速度和位置参数，并确定速度、位置的取值范围；
[0032]
(3)运行磁悬浮转子系统的仿真模型，计算适应度函数获得粒子的适应度值，将每个粒子的位置作为其初始个体最优解p
best
；找出其中最小的适应度值，将该粒子的位置作为粒子群的初始全局最优解g
best
；
[0033]
(4)根据下式更新粒子的速度：
[0034][0035]
式中，v为粒子的速度；i为第i个粒子，i＝1,2,
…
,n；d为粒子的某一维度，d＝1,2,
…
,d；t为当前迭代次数；ω为惯性权重；c1、c2为学习因子，也称为加速度常数；r1、r2为在0～1之间均匀分布的随机数；
[0036]
根据下式更新粒子的位置；
[0037][0038]
式中，x为粒子的位置；i为第i个粒子，i＝1,2,
…
,n；d为粒子的某一维度，d＝1,2,
…
,d；t为当前迭代次数；
[0039]
(5)运行磁悬浮转子系统的仿真模型，计算粒子的适应度值；
[0040]
(6)若适应度值优于历史个体最优解p
best
对应的适应度值，则更新个体最优解p
best
；
[0041]
(7)若适应度值优于历史全局最优解g
best
对应的适应度值，则更新全局最优解g
best
；
[0042]
(8)重复步骤(4)～(7)，遍历种群中所有粒子后，若已满足优化精度即适应度值小于最小适应度值或已达到最大迭代次数，则退出，最终获得的全局最优解g
best
即为权重因子w和控制增益k1、k2参数优化结果；否则返回步骤(4)中。
[0043]
完成步骤(1)～(8)后，将通过粒子群算法进行离线优化后获得的二阶双模奇次重复控制器w、k1、k2参数值应用于磁悬浮转子系统中，进一步提高二阶双模奇次重复控制器的奇次谐波抑制精度，实现磁悬浮转子奇次谐波振动力的高精度抑制。
[0044]
本发明基本原理在于：磁悬浮转子系统的主要振动源为质量不平衡和传感器谐波，二者使磁悬浮控制力矩陀螺在运行的过程中产生谐波振动力，谐波振动力通过基座传递到航天器平台，会严重影响航天器平台的载荷性能。根据频谱分析可知，磁悬浮控制力矩陀螺中主导谐波分量为奇次谐波。本发明针对磁悬浮控制力矩陀螺的磁悬浮转子奇次谐波振动力，建立包含质量不平衡和传感器谐波的磁悬浮转子动力学模型，基于二阶双模奇次重复控制器对磁悬浮转子的奇次谐波振动力进行抑制，并采用粒子群算法实现二阶双模奇次重复控制器参数的离线优化。二阶双模奇次重复控制器在奇次谐波频率点处产生无穷增益，以反馈的形式接入原始的磁悬浮转子系统中实现奇次谐波振动力的抑制；提出一种新的稳定性判据，通过合理设计相位补偿环节并合理选取权重因子和控制增益，保证磁悬浮转子系统在工作转频范围内的稳定性，并具有一定的频率波动鲁棒性和较快的动态收敛速度；根据性能要求设计适应度函数，采用粒子群算法智能选取二阶双模奇次重复控制器中权重因子和控制增益的最优值。
[0045]
本发明与现有技术相比的优点在于：
[0046]
(1)本发明在提出的二阶双模奇次重复控制器中引入权重因子w和控制增益k1、k2；相比于传统重复控制器，二阶双模奇次重复控制器可通过调节权重因子w的取值在谐波频率点附近产生更大的增益，提高了磁悬浮转子转频摄动时的频率波动鲁棒性；重复控制器的两条控制通道有独立的控制增益k1、k2，可分别调节k1、k2的取值来调整磁悬浮转子系统的动态响应速度和稳态收敛精度；同时，相比于二阶重复控制器，二阶双模奇次重复控制器仅针对奇次谐波分量进行抑制，将延迟单元数减少一半，节约了计算资源和内存空间，加快
了控制系统的收敛速度。
[0047]
(2)本发明提出了加入二阶双模奇次重复控制器后磁悬浮转子系统的稳定性判据，根据该判据设计相位补偿环节并确定权重因子和控制增益的参数值，保证在工作转频范围内控制系统的稳定性，实现任意给定转速下磁悬浮转子奇次谐波振动力的高精度抑制。
[0048]
(3)本发明针对二阶双模奇次重复控制器参数较多、不易确定最优参数值的问题，根据性能要求，选择itae准则作为适应度函数，建立加入二阶双模奇次重复控制器后磁悬浮转子系统的仿真模型，采用粒子群算法智能选取权重因子w和控制增益k1、k2的最优值，实现二阶双模奇次重复控制器的离线参数优化。
附图说明
[0049]
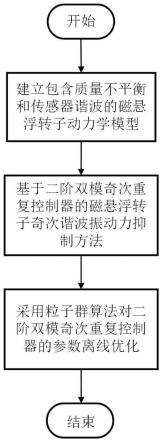
图1为本发明的流程图；
[0050]
图2为磁悬浮转子系统结构示意图，其中，1为磁悬浮转子，2为径向磁轴承，3为径向位移传感器，4为转子惯性轴，5为转子几何轴；
[0051]
图3为原始的磁悬浮转子系统控制框图；
[0052]
图4为二阶双模奇次重复控制器结构图；
[0053]
图5为基于二阶双模奇次重复控制器的磁悬浮转子系统控制框图；
[0054]
图6为采用粒子群算法实现二阶双模奇次重复控制器参数离线优化的流程图。
具体实施方式
[0055]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整的描述，显然，所描述的实施例仅为本发明的一部分实施例，而不是全部的实施例，基于本发明中的实施例，本领域的普通技术人员在不付出创造性劳动的前提下所获得的所有其他实施例，都属于本发明的保护范围。
[0056]
如图1所示，本发明一种基于粒子群参数优化二阶双模奇次重复控制器的磁悬浮转子奇次谐波振动力抑制方法的实施过程是：首先建立包含质量不平衡和传感器谐波的磁悬浮转子动力学模型；然后基于二阶双模奇次重复控制器对磁悬浮转子奇次谐波振动力进行抑制，最后采用粒子群算法对二阶双模奇次重复控制器的权重因子和控制增益进行参数离线优化。二阶双模奇次重复控制器能实现奇次谐波分量的精确抑制，提高系统在转子转频摄动时的频率波动鲁棒性，同时减少延迟单元数以提高计算效率，加快系统的收敛速度。提出一种新的稳定性判据，保证加入二阶双模奇次重复控制器后磁悬浮转子系统在工作转频范围内的稳定性。采用粒子群算法实现二阶双模奇次重复控制器最优参数值的智能选取，进一步提高控制系统奇次谐波振动力的抑制性能。本发明中的二阶双模奇次重复控制器结构简单，在实际应用中很方便，适用于存在转子质量不平衡和传感器谐波的磁悬浮转子系统奇次谐波振动力的抑制。
[0057]
下面具体实现如下：
[0058]
步骤(1)建立包含质量不平衡和传感器谐波的磁悬浮转子动力学模型
[0059]
本发明的应用对象为磁悬浮控制力矩陀螺的磁悬浮转子系统。其结构如图2所示，定义o点为径向磁轴承定子中心，x轴和y轴相互正交且分别与两对径向磁轴承连线平行，z
轴沿径向磁轴承定子中心线，oxy为广义坐标系，cg和ci分别是磁悬浮转子的几何中心和质量中心，1为磁悬浮转子，2为径向磁轴承，3为径向位移传感器，4为转子惯性轴，5为转子几何轴，磁轴承和位移传感器对称分布于转子的a、b两端，lm为磁轴承所在平面到定子中心o点所在平面的距离，ls为位移传感器所在平面到定子中心o点的距离。在广义坐标系oxy下，磁悬浮转子的几何轴和惯性轴位移表示为：
[0060]
qg＝[x
g β
g ygꢀ‑
αg]
t
[0061]
qi＝[x
i β
i yiꢀ‑
αi]
t
[0062]
式中，qg为转子的几何轴位移，qi为转子的惯性轴位移；xg和xi为x轴方向的平动位移；βg和βi为y轴方向的转动位移；yg和yi为y轴方向的平动位移；αg和αi为x轴方向的转动位移；t为向量的转置。
[0063]
根据牛顿第二运动定律和陀螺技术方程，矩阵形式的磁悬浮转子动力学模型表示为：
[0064][0065]
式中，m为广义质量矩阵，g为陀螺矩阵，f为广义力矢量，和分别为惯性轴位移的二次微分和一次微分。
[0066]
质量不平衡使转子的惯性轴和几何轴不重合，二轴的偏差导致了转子产生与转速同频的振动。质量不平衡表示为：
[0067][0068]
式中，δq
x
和δqy分别为转子在x轴、y轴方向的静不平衡分量；δq
α
和δq
β
分别为转子在x轴、y轴方向的动不平衡分量；ε和χ分别为静不平衡的幅值和初始相位；σ和δ分别为动不平衡的幅值和初始相位；ω为转子的转速；t为时间。
[0069]
位移传感器检测到的位移信号与磁悬浮转子几何轴的真实位移之间存在偏差，该偏差引起传感器谐波，导致了转子产生与转速同频和倍频的振动。传感器谐波表示为：
[0070][0071]
式中，q
srax
、q
srbx
、q
sray
和q
srby
分别为四对位移传感器的谐波分量；s
ax0
、s
bx0
、s
ay0
和s
by0
分别表示各方向传感器谐波中的直流分量，是传感器检测面中心线和传感器电性能中心线不重合引起的，不造成转子的谐波振动，可通过位移调理电路消除；s
ai
和s
bi
分别为a、b两端传感器谐波的第i次谐波分量的幅值；ξ
asi
和ξ
bsi
分别为a、b两端传感器谐波的第i次谐
波分量的初始相位；i为第i次谐波；n为总的谐波次数。
[0072]
由上述分析可知，转子质量不平衡和传感器谐波会在磁悬浮转子系统中引入同频和倍频的扰动，使转子产生谐波振动力。
[0073]
由于转子仅在平衡位置附近产生小位移运动，可将非线性磁轴承力通过taylor展开得到线性化磁轴承力。线性化磁轴承力表示为：
[0074]fm
＝kiim+khqm[0075]
式中，fm为径向磁轴承力；ki和kh分别为电流刚度和位移刚度；im为四对径向磁轴承的线圈电流，qm为转子的径向位移。磁轴承谐波振动力包含电流刚度力和位移刚度力两部分，其中电流刚度力占磁轴承振动力的主要部分，因此抑制磁轴承线圈电流中的谐波分量可以抑制大部分振动力。
[0076]
最终建立包含质量不平衡和传感器谐波的磁悬浮转子动力学模型，表示为：
[0077][0078]
式中，m为转子的质量；q
srx
和q
sry
分别为x轴、y轴方向的传感器谐波分量；gc(s)为磁轴承控制器的传递函数；gw(s)为功率放大器的传递函数；ks为位移传感器的增益系数；s为拉普拉斯算子；
·
(s)为对应物理量的拉普拉斯变换表达式。
[0079]
包含质量不平衡和传感器谐波的磁悬浮转子系统控制框图如图3所示，图中gc(s)为磁轴承控制器的传递函数；gw(s)为功率放大器的传递函数；ki和kh分别为电流刚度和位移刚度；ks为位移传感器的增益系数；xi和xg分别为x轴方向的惯性轴位移和几何轴位移；δq
x
为x轴方向的质量不平衡分量；q
srx
为x轴方向的传感器谐波分量；xs为位移传感器的输出信号；e
x
为x轴方向给定参考信号和位移传感器输出信号之间的偏差信号；m为转子的质量；s为拉普拉斯算子。
[0080]
步骤(2)：设计基于二阶双模奇次重复控制器的磁悬浮转子奇次谐波振动力抑制方法
[0081]
设计二阶双模奇次重复控制器，以包含同频和倍频扰动分量的线圈电流作为输入，基于重复控制器的内模原理跟踪提取线圈电流中谐波分量，并将输出反馈至原控制系统的功率放大器输入端，实现奇次谐波振动力的有效抑制，该模块的设计包括以下两个步骤：
[0082]
①
二阶双模奇次重复控制器结构方法，由于磁悬浮转子系统线圈电流的主导谐波成分为奇次谐波分量，设计在奇次谐波频率点处产生无穷增益的重复控制器内模结构；在重复控制器中引入权重因子w和控制增益k1、k2，权重因子可提高转子转频摄动时控制系统的频率鲁棒性，控制增益可调节控制系统的响应速度和稳态精度。
[0083]
②
针对加入二阶双模奇次重复控制器的磁悬浮转子系统，提出一个新的稳定性判据，该判据给出了权重因子和控制增益的关系和参考范围，以及系统相位的取值范围：适当调节w和k
rc
的取值可兼顾系统的频率波动鲁棒性和响应速度；根据稳定性判据和系统函数的相频特性合理设计相位补偿环节，可提高系统的稳定性，拓宽控制增益的取值上限，改善系统的动态收敛速度和稳态抑制精度。
[0084]
进一步的，所述的步骤(2)奇次谐波振动力抑制方法为：
[0085]
①
二阶双模奇次重复控制器的结构设计
[0086]
二阶双模奇次重复控制器的传递函数表示为：
[0087][0088]
式中，为二阶双模奇次重复控制器的内模传递函数；k1、k2分别为重复控制器两个通道的控制增益；w为权重因子；n为延迟单元数，等于采样频率和转子转频的比值；q(z)为提高系统稳定性的低通滤波器，截止频率为ωc；c(z)为使闭环系统满足稳定性判据的相位补偿函数；l(z)＝z
l
为具有一固定超前角θ
l
(ω)＝lωts的线性相位超前补偿函数。二阶双模奇次重复控制器的结构如图4所示，图中i(z)为输入重复控制器的线圈电流信号，i
rc
(z)为重复控制器输出的线圈电流信号；
·
(z)为对应物理量的z变换表达式。
[0089]
由于磁悬浮转子的工作转频远小于低通滤波器q(z)的截止频率ωc，在(0,ωc)的频率范围内q(z)可近似为1。二阶双模奇次重复控制器的极点表示为：
[0090][0091]
二阶双模奇次重复控制器的极点均在奇次谐波频率点处，即二阶双模奇次重复控制器在奇次谐波频率点处产生无穷增益，因此基于二阶双模奇次重复控制器的磁悬浮转子系统可抑制频率响应中的奇次谐波成分。磁悬浮转子不可避免的存在转频在设定频率附近小范围波动的问题，相比于传统重复控制器，二阶双模奇次重复控制器通过调节权重因子w，可在奇次谐波频率点附近产生更大的增益，从而提高系统的频率波动鲁棒性。同时，通过适当调节控制增益k
rc
，可改善系统的动态特性和稳态精度。相比于二阶重复控制器，二阶双模奇次重复控制器仅针对奇次谐波分量进行抑制，将延迟单元总数由2n降低为n，减少计算资源，节约内存空间，加快控制系统的收敛速度。
[0092]
②
加入二阶双模奇次重复控制器后磁悬浮转子系统的稳定性判据
[0093]
为简化分析，令低通滤波器q(z)＝1，控制增益k1＝k2＝k
rc
。二阶双模奇次重复控制器的内模传递函数可重写为：
[0094][0095]
基于二阶双模奇次重复控制器的磁悬浮转子系统控制框图如图5所示，图中gc(z)为磁轴承控制器的传递函数；gw(z)为功率放大器的传递函数；g
p
(z)为磁悬浮转子的传递函数；g
sdorc
(z)为二阶双模奇次重复控制器的传递函数；ks为位移传感器的增益系数；r(z)为位移参考信号，通常为0；d(z)为质量不平衡和传感器谐波的等效扰动信号；i(z)为输入重复控制器的线圈电流信号；i
rc
(z)为重复控制器输出的线圈电流信号。
[0096]
定义磁悬浮转子系统的系统函数为：
[0097][0098]
式中，gc(z)为磁轴承控制器的传递函数；gw(z)为功率放大器的传递函数；ks为位移传感器的增益系数；g
p
(z)为磁悬浮转子的传递函数。
[0099]
假设系统函数f(z)的频率响应为相位补偿函数c(z)的频率响应为线性相位超前补偿函数l(z)＝z
l
的频率响应为其中，af(ω)、ac(ω)、a
l
(ω)＝1是幅值，θf(ω)、θc(ω)、θ
l
(ω)是相位。定义m(ω)＝ac(ω)af(ω)，λ(ω)＝θc(ω)+θf(ω)+θ
l
(ω)。ω为角频率。
[0100]
若满足下列条件，则加入二阶双模奇次重复控制器后的磁悬浮转子系统是渐近稳定的：
[0101]
条件1：原始的磁悬浮转子系统是渐进稳定的；
[0102]
条件2：加入二阶双模奇次重复控制器后磁悬浮转子系统的控制增益k
rc
、权重因子w和相位λ(ω)满足下式：
[0103][0104]
根据稳定性判据合理设计相位补偿函数c(z)以及线性相位超前补偿函数l(z)的超前拍数l，并选择合适的控制增益k
rc
、权重因子w，可保证加入二阶双模奇次重复控制器后磁悬浮转子系统的稳定性。
[0105]
步骤(3)：采用粒子群算法对二阶双模奇次重复控制器的参数进行离线优化
[0106]
pso算法基于对鸟类、鱼群觅食行为的模拟，该算法通过在整个种群的区域内进行随机迭代搜索，寻找最优解以实现问题的优化。在对种群初始化后，种群中每个粒子都是优化问题的潜在解。每个粒子的状态可通过三个量来描述：速度、位置和适应度值。速度和位置反映了粒子当前的运动状况；适应度值通过计算适应度函数获得，适应度值越小的粒子越逼近全局最优解。个体最优解p
best
是每个粒子在历次迭代中获得最小适应度值所对应的位置，全局最优解g
best
是整个粒子群搜索到最小适应度值时的位置。采用粒子群算法实现二阶双模奇次重复控制器参数w、k1、k2离线优化的流程如图6所示，具体步骤为：
[0107]
①
建立基于二阶双模奇次重复控制器的磁悬浮转子系统仿真模型，选择时间乘绝对误差积分(itae)准则作为适应度函数，itae准则表示为：
[0108][0109]
式中，j为适应度函数值；e(t)为线圈电流实际值和参考值之间的偏差量；t为时间；
[0110]
②
将二阶双模奇次重复控制器的参数w、k1、k2作为粒子群算法的位置参数，初始化粒子群的规模n、维度数d、最大迭代次数、最小适应度值、速度、位置参数，并确定速度、位置
参数的取值范围；
[0111]
③
运行磁悬浮转子系统的仿真模型，计算适应度函数获得粒子的适应度值，将每个粒子的位置作为其初始个体最优解p
best
；找出其中最小的适应度值，将该粒子的位置作为粒子群的初始全局最优解g
best
；
[0112]
④
根据下式更新粒子的速度：
[0113][0114]
式中，v为粒子的速度；i为第i个粒子，i＝1,2,
…
,n；d为粒子的某一维度，d＝1,2,
…
,d；t为当前迭代次数；ω为惯性权重；c1、c2为学习因子，也称为加速度常数；r1、r2为在0～1之间均匀分布的随机数；
[0115]
根据下式更新粒子的位置；
[0116][0117]
式中，x为粒子的位置；i为第i个粒子，i＝1,2,
…
,n；d为粒子的某一维度，d＝1,2,
…
,d；t为当前迭代次数；
[0118]
⑤
运行磁悬浮转子系统的仿真模型，计算粒子的适应度值；
[0119]
⑥
若适应度值优于历史个体最优解p
best
对应的适应度值，则更新个体最优解p
best
；
[0120]
⑦
若适应度值优于历史全局最优解g
best
对应的适应度值，则更新全局最优解g
best
；
[0121]
⑧
重复步骤
④
～
⑦
，遍历种群中所有粒子后，若已满足优化精度(适应度值小于最小适应度值)或已达到最大迭代次数，则退出算法，最终获得的全局最优解g
best
即为权重因子w和控制增益k1、k2参数优化结果；否则返回步骤
④
。
[0122]
完成步骤
①
～
⑧
后，将通过粒子群算法进行离线优化后获得的二阶双模奇次重复控制器w、k1、k2参数值应用于磁悬浮转子系统中，进一步提高二阶双模奇次重复控制器的奇次谐波抑制精度，实现磁悬浮转子奇次谐波振动力的高精度抑制。
[0123]
尽管上面对本发明说明性的具体实施方式进行了描述，以便于本技术领域的技术人员理解本发明，且应该清楚，本发明不限于具体实施方式的范围，对本技术领域的普通技术人员来讲，只要各种变化在所附的权利要求限定和确定的本发明的精神和范围内，这些变化是显而易见的，一切利用本发明构思的发明创造均在保护之列。