一种基于凸优化的非平坦地形下无人车轨迹规划方法

1.本发明属于无人车轨迹规划技术领域，具体涉及一种基于凸优化的非平坦地形下无人车轨迹规划方法。


背景技术：

2.近年来，随着科技的发展，无人自主机器人在许多领域均发挥着重要的作用，例如地下矿井，精准农业，灾后救援等，无人车则是其中的主要对象。在针对无人车不同方向的诸多研究中，路径规划是必不可少且至关重要的一环。虽然无人车路径规划的研究层出不穷，但非平坦地图下的规划工作则十分稀少。现阶段针对非平坦地图的路径规划研究主要有两种方法，分别是基于图搜索的算法和基于采样的算法。其中前者将空间离散之后为无人车规划折线路径，而后者并未考虑路径规划的最优性。在此基础上，本发明充分考虑到实际地表崎岖、不平坦的特性，开展了基于凸优化的非平坦地形下无人车轨迹规划研究，旨在为无人车规划一条既满足运动学特性的要求，又节约能耗和时间的平滑轨迹。


技术实现要素：

3.针对无人车存在执行机构饱和约束等问题，本发明提供一种基于凸优化的非平坦地形下无人车轨迹规划方法，能够在节约能耗和时间的同时，为无人车规划一条既满足运动学特性要求的平滑轨迹。本发明主要应用于给定无人车初始时刻与终点时刻位置以及栅格化之后非平坦地形地图基础上的时间-能耗最优轨迹规划。
4.为达到上述目的，本发明采用的技术方案为：
5.一种基于凸优化的非平坦地形下无人车轨迹规划方法，包括以下步骤：
6.(1)通过栅格化给定非平坦地图模型，建立无人车在任意方向相邻节点之间运动的能耗模型；
7.(2)在步骤(1)的基础上设计启发式函数，并通过a*搜索算法生成一条能耗最优的初始路径；
8.(3)通过修剪步骤(2)中初始路径的路标点以生成运动走廊；
9.(4)在步骤(3)的基础上设计目标函数，并通过施加不同约束将其转换到二次约束二次规划的框架下求解得到优化后初始轨迹，并进一步调整时间参数以生成最终轨迹。
10.进一步地，所述步骤(1)中，
11.在从当前点nc处运动到邻居节点nn处的过程中，消耗的能量e
t
(nc,nn)为：
[0012][0013]
其中，m表示无人车的质量，g为重力加速度，μ为动摩擦系数，φ为邻域节点之间的倾角，φ
max
为最大爬坡倾角，φb为临界倾角，φ
min
为最小临界倾角，由斜坡的静摩擦系数μs确定：φ
min
＝-arctan(μs)；s(ni,nj)表示节点ni和nj之间的欧氏距离；
[0014]
其中，无人车的在饱和约束及安全约束共同作用下的最大爬坡倾角为φ
max
＝max(φf,φs)，其中，在静摩擦力的作用下保持无人车静止的最大爬坡倾角φs＝arctan(μ
s-μ)，其中μs为斜坡的静摩擦系数，无人车在存在牵引力的前提下最大爬坡倾角φf为：
[0015][0016]
其中，f
max
为最大牵引力；
[0017]
无人车在nc处原地转向的能耗模型为：
[0018]er
(nc,ψ)＝μmg
·
(π-ψ)
·r[0019]
其中，ψ∈[0,π]是无人车从ni到nj经过nc时的转向角，nc是ni的邻居，nj是nc的邻居，r＞0，是无人车的原地转向半径；
[0020]
从节点nr到当前点nc真实消耗的能量为：
[0021][0022]
进一步地，所述步骤(2)中的启发式函数h(nc)为：
[0023][0024]
其中，δ(ni,nj)表示节点ni和nj之间的垂直距离。
[0025]
通过所述a*搜索算法生成一条初始路径。
[0026]
进一步地，所述步骤(3)包括在x-y平面内为修剪过路标点的路径生成凸的运动走廊；运动走廊的长度由子路径的长度决定，宽度通过人为设定。
[0027]
进一步地，所述步骤(4)中，所述目标函数为轨迹f(t)三阶导数的平方，即：
[0028][0029]
其中，是包含2个方向(η∈{x,y})、m个分段(i＝1,2,
…
,m)的n阶多项式(j＝0,1,
…
,n)轨迹所有控制点的向量，q0是目标函数的海森矩阵；
[0030]
其中，对于任一方向轨迹f
η
(t)，有：
[0031]
[0032]
其中，η∈{x,y}表示方向，t1,t2,
…
,tm为每段轨迹的终端时刻，无人车走完整条轨迹一共耗时t＝t
m-t0，δti＝t
i-t
i-1
则是一个比例系数，表示每段轨迹所用时长，用于将真实的不同时刻统一至区间[0,1]在等式约束中，限制轨迹在初末时刻状态，为：
[0033]fη
(t0)＝p
η0
,f
η
(tm)＝p
ηe
[0034]f′
η
(t0)＝v
η0
,f
′
η
(tm)＝v
ηe
[0035]f″
η
(t0)＝a
η0
,f
″
η
(tm)＝a
ηe
[0036]
其中，p,v,a分别表示无人车的位置、速度、加速度，{
·
}0和{
·
}e表示初始时刻和终止时刻的状态，η∈{x,y}表示方向；
[0037]
使得最终轨迹的平滑需要使相邻曲线之间的各阶导数连续，即：
[0038][0039][0040][0041]
其中，和分别为第i段贝塞尔轨迹的初始时刻和末端时刻，i＝1,2,
…
,m-1；
[0042]
轨迹的不等式约束是针对每段轨迹控制点的约束，为其中为第i个运动走廊，i＝1,2,
…
,m；
[0043]
将相邻轨迹交点约束在以路径交点为中心，运动走廊宽度为直径的圆中，即其中wpi表示第i个路标点的位置，ri表示第i个运动走廊相交区域的半径，i＝1,2,
…
,m-1；
[0044]
饱和约束表现为速度约束和加速度约束，有：
[0045][0046][0047]
其中，v
max
为最大速度，a
max
为最大加速度；
[0048]
当前的优化问题转化为：
[0049][0050][0051]aeq
c＝b
eq
,
[0052]aieq
c≤b
ieq
.
[0053]
通过求解器得到上述优化问题的数值解；
[0054]
最后使用梯度下降法进一步调整时间参数达到时间-能耗最优。
[0055]
本发明与现有技术相比，优点在于：
[0056]
(1)本发明充分考虑了无人车原地转向消耗的能量以及安全约束，建立了更加全面的无人车能耗模型，并通过设计有效的启发式能耗函数，提出了基于a*搜索算法的能耗最优路径规划方法，该方法可以在非平坦地图下为无人车规划出能耗最优可行路径。
[0057]
(2)本发明通过生成每段子路径的运动走廊，将分段贝塞尔轨迹限制在运动走廊
内部，以保证平滑轨迹贴合初始折线路径。
[0058]
(3)本发明在提出目标函数的基础上，通过对基于贝塞尔曲线的轨迹施加各种约束(等式约束、不等式约束、二次约束等)，将优化问题转化为标准的二次约束二次规划问题，并使用求解器得到数值解，进而计算出无人车在每个时刻的状态。
[0059]
(4)本发明通过设计分段贝塞尔轨迹的时间重分配方法，进一步优化了无人车在每段子轨迹上运动的时间，缩短了整体时长。
附图说明
[0060]
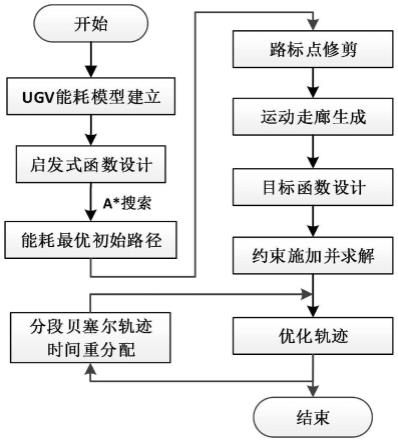
图1为本发明的一种基于凸优化的非平坦地形下无人车轨迹规划方法流程框图；
[0061]
图2为本发明典型情况下路标点修剪示意图；
[0062]
图3为本发明的8种不同方向子路径生成的运动走廊示意图；
[0063]
图4a，图4b，图4c为本发明优化前后的轨迹及速度、加速度曲线对比；其中，图4a为不同方法生成路径对比，图4b为速度随时间变化曲线，图4c为加速度随时间变化曲线。
具体实施方式
[0064]
为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。此外，下面所描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间未构成冲突就可以相互组合。
[0065]
本发明的一种基于凸优化的非平坦地形下无人车轨迹规划方法，在给定无人车初始时刻与终点时刻位置以及栅格化之后非平坦地形地图的基础上，轨迹规划方法包括以下步骤：首先，建立无人车的能耗模型，以确定无人车在地图上任意位置处前往相邻接点所产生的能耗；其次，设计有效的启发式函数并基于a*搜索算法生成能耗最优初始路径；然后，经过修剪初始路径的路标点生成运动走廊，用以约束最终轨迹位置及运动学特性；进一步，设计目标函数并施加等式约束、不等式约束以及二次约束，得到优化后的初始轨迹；最后，通过对生成分段贝塞尔轨迹所用时间进行重分配得到优化后的最终轨迹。本发明的一种基于凸优化的非平坦地形下无人车轨迹规划方法的原理框图如图1所示，具体实施步骤如下：
[0066]
第一步，建立无人车能耗模型。无人车在一个倾角为θ的斜坡上，其运动主要有两种情况：在第一种情况下，无人车在斜坡上直上直下，其运动方向与运动方向在水平面上投影的夹角φ1与斜坡倾角θ相同，即φ1＝θ；在第二种情况下，无人车在坡上斜着运动，此时其运动方向与运动方向在水平面上投影的夹角φ2小于斜坡倾角θ，即φ2＜θ。本发明在建立无人车能耗模型时忽略斜面倾角θ，仅考虑邻域节点之间的倾角φ。另外，暂时假设无人车的运动是匀速的，即所受合力为0。
[0067]
当无人车在斜坡上运动时，其所受到的力主要有3个，分别是竖直向下的重力g＝mg，与斜面平行的牵引力f
x
和摩擦力f＝μmg cosφ，其中m表示无人车的质量，g为重力加速度，μ为动摩擦系数。当无人车沿斜坡向上运动时，为保证其所受合力始终为0，需要使自身产生的牵引力与摩擦力和重力的合力相同，即f
x
＝mg(μcosφ+sinφ)。然而，由于无人车存在一定的饱和约束，假设其能够提供的最大牵引力为f
max
，那么无人车在存在牵引力的前提下最大爬坡倾角φf的计算公式为：
[0068][0069]
然而，无人车在爬坡过程中始终存在着牵引力消失的可能。为了规避上述风险，无人车的最大爬坡倾角需使其仅在静摩擦力fs的作用下能够保持静止。此时，无人车的最大爬坡倾角为φs＝arctan(μ
s-μ)，其中μs为斜坡的静摩擦系数。因此，无人车的在饱和约束及安全约束共同作用下的最大爬坡倾角为φ
max
＝max(φf,φs)。
[0070]
当无人车沿斜坡向下运动时，无人车依旧受到上述三个力的共同作用。然而，由于重力在斜面上的分量和摩擦力的方向相反，所以必定存在一个临界倾角φb使得当φ＝φb时无人车不需要牵引力，仅仅依靠重力即可匀速下坡，此时μmg cosφb＝mg sinφb，即φb＝-arctan(μ)。值得注意的是，当φ＜φb时，无人车将向下加速，因此需要不断进行制动以抵消加速度产生的速度变化。同样地，无人车在下坡过程中依旧有一个最小临界倾角φ
min
，使得当φ＜φ
min
时，无人车即使完全制动也无法保证匀速的行驶。该最小临界倾角φ
min
由斜坡的静摩擦系数μs确定，为φ
min
＝-arctan(μs)。
[0071]
综上，在从当前点nc处运动到邻居节点nn处的过程中消耗的能量e
t
(nc,nn)为：
[0072][0073]
其中，δ(ni,nj)表示节点ni和nj之间的垂直距离。
[0074]
另外，无人车在nc处原地转向的能耗模型为：
[0075]er
(nc,ψ)＝μmg
·
(π-ψ)
·r[0076]
其中，ψ∈[0,π]是无人车从ni到nj经过nc时的转向角，nc是ni的邻居，nj是nc的邻居，r＞0是无人车的原地转向半径。
[0077]
综上，从节点nr到当前点nc真实消耗的能量为：
[0078][0079]
第二步，设计a*搜索算法的启发式函数。节点ng为终点，当φ(nc,ng)＜φ
min
时，无人车下坡时倾角过大，此时即使完全制动也无法使其匀速运动。但是通过进行“之”字形的折线运动可以避免上述情况，并将能耗控制为零，即h(nc)＝0。然而，在无人车实际从当前点nc处运动到终点ng处的过程中，很有可能并不是完全下降的，所以很有可能产生一定的能耗，即e
t
(nc,ng)≥0，此时h(nc)≤e
t
(nc,ng)，启发式函数有效。
[0080]
当φ
min
≤φ(nc,ng)≤φb时，无人车不需要沿着折线往复运动以规避风险，只需考虑nc和ng之间的虚拟直线并通过制动到达目标，此时估计的启发式能耗依旧为零，即h(nc)＝0。同样地，虽然无人车在这条虚拟直线上的能耗为零，但是实际情况中很有可能存在更复杂的情况，因此消耗的能量通常不为零，即h(nc)≤e
t
(nc,ng)，此时启发式函数有效。
[0081]
当φb＜φ(nc,ng)≤φ
max
时，对于从当前点nc处运动到终点ng的路径中每一个子路径(ni,nj)∈(nc,ng)，其倾角φ(ni,nj)有两种可能性，分别是φb＜φ(ni,nj)≤φ
max
和φ
min
≤φ(ni,nj)≤φb，剩下的两个倾角范围由于可逐步分解所以不会真实存在。简单推导可以
发现，当所有的子路径倾角都在[φb,φ
max
]范围内时，e(nc,ng)＝mg[μcosφ+sinφ]
·
s，其中s＝s(ni,nj)表示节点ni和nj之间的欧氏距离。因此，当φb＜φ(nc,ng)≤φ
max
时，e(nc,ng)≥mg[μcosφ+sinφ]
·
s，令其为从当前点nc处运动到终点ng的无人车消耗能量估计值，即可保证启发式函数的有效性。
[0082]
当φ(nc,ng)＞φ
max
时，与之前类似，无人车规划的路径依旧可以分解成倾角为[φ
min
,φb]或[φb,φ
max
]的诸多子路径，同理可以证明启发式函数依旧是有效的，此处不再赘述。
[0083]
综上所述，所设计基于a*搜索算法的启发式函数h(nc)为：
[0084][0085]
其中，δ(ni,nj)表示节点ni和nj之间的垂直距离。
[0086]
接下来通过a*搜索算法即可生成一条初始路径。
[0087]
第三步，修剪路标点以生成运动走廊。
[0088]
初始路径中路标点(即转折点)的个数会直接影响最终生成平滑轨迹的效果，更严重的甚至会使问题无解，图2给出了典型的临近节点内路标点多次转折情形的修剪示意图，其中左图为初始路标点及初始路径，右图为修剪后的路标点及路径。
[0089]
进一步，在x-y平面内为修剪过路标点的路径生成凸的运动走廊。在平面内相邻路标点之间的子路径只有8个可能的方向，图3给出了每个方向运动走廊的示意图。图3中黑色点为子路径的起点，黑色箭头为子路径的终点，阴影区域为该路径的运动走廊，每个灰色方块代表地图中的一个节点。运动走廊的长度由子路径的长度决定，而宽度则是人为设定的。通过将其宽度设置的足够小，可以保证优化之后的轨迹可以比较贴近路径，并使无人车运动过程中产生较低的能耗。
[0090]
第四步，目标函数设计及约束施加。
[0091]
一条n次贝塞尔曲线可表示为：
[0092][0093]
其中，t∈[0,1]为单位化之后的时间，{c0,c1,
…
,cn}表示曲线的n+1个控制点，b
ni
(t)是伯恩斯坦基函数：
[0094][0095]
假设优化之后的轨迹f(t)＝[f
x
(t),fy(t)]由m条分段贝塞尔曲线构成，其中f
x
(t)和fy(t)分别表示轨迹在x和y方向上的分量。对于任一方向轨迹f
η
(t)，有：
[0096][0097]
其中，η∈{x,y}表示方向，t1,t2,
…
,tm为每段轨迹的终端时刻，无人车走完整条轨迹一共耗时t＝t
m-t0，而δti＝t
i-t
i-1
则是一个比例系数，表示每段轨迹所用时长，用于将真实的不同时刻统一至区间[0,1]，是第i段轨迹在η方向上的第j个控制点，i＝1,2,
…
,m，j＝0,1,
…
,n。由于考虑的无人车饱和约束最高为二阶，即加速度a(t)，所以为了保证无人车运动过程中各阶导数(位置、速度、加速度)连续，将目标函数设计为轨迹f(t)三阶导数的平方，即：
[0098][0099]
其中，是包含轨迹所有控制点的向量，q0是目标函数的海森矩阵。
[0100]
接下来需要对目标函数施加一些约束以便于生成一条平滑、安全并且符合执行机构饱和特性的轨迹。具体地，在等式约束中，需要限制轨迹在初末时刻状态，为：
[0101]fη
(t0)＝p
η0
,f
η
(tm)＝p
ηe
[0102]f′
η
(t0)＝v
η0
,f
′
η
(tm)＝v
ηe
[0103]f″
η
(t0)＝a
η0
,f
″
η
(tm)＝a
ηe
[0104]
其中，p,v,a分别表示无人车的位置、速度、加速度，{
·
}0和{
·
}e表示初始时刻和终止时刻的状态，η∈{x,y}表示方向。另外，由于轨迹f
η
(t)是由多条贝塞尔曲线构成的，为了最终轨迹的平滑需要使相邻曲线之间的各阶导数连续，即：
[0105][0106][0107][0108]
其中，t
i-和t
i+
(i＝1,2,
…
,m-1)分别为第i段贝塞尔轨迹的初始时刻和末端时刻。
[0109]
由于贝塞尔曲线的凸包性质能够将轨迹严格限制在由控制点组成的凸包内。所以对于某一段贝塞尔轨迹来说，只需将其控制点均限制在凸的运动走廊中，即可约束整条轨迹。基于此，轨迹的不等式约束主要是针对每段轨迹控制点的约束，为：其中为第i个运动走廊。
[0110]
二次约束主要有两种，一是相邻分段贝塞尔轨迹的连接点位置约束，二是无人车
的饱和约束。由于每段轨迹在末时刻的位置需要限制在运动走廊内，所以需要将每两条相邻轨迹的交点限制在相邻运动走廊的相交区域。为了在保证凸性的同时简化约束施加难度，本发明将相邻轨迹交点约束在以路径交点为中心，运动走廊宽度为直径的圆中，即其中wpi(i＝1,2,
…
,m-1)表示第i个路标点的位置，ri表示第i个运动走廊相交区域的半径。
[0111]
另外，在实际情况下执行机构存在一定的饱和约束。饱和约束的施加也使最终生成的轨迹符合无人车的运动学特性。具体地，饱和约束表现为速度约束和加速度约束。由于贝塞尔曲线的另一特性是其各阶导数仍是贝塞尔曲线，所以有：
[0112][0113][0114]
其中，v
max
为最大速度，a
max
为最大加速度。
[0115]
当前的优化问题可转化为：
[0116][0117][0118]aeq
c＝b
eq
,
[0119]aieq
c≤b
ieq
.
[0120]
其为一个典型的二次约束二次规划问题，很容易通过求解器得到数值解。最后使用梯度下降法可进一步调整时间参数以达到时间-能耗最优。
[0121]
利用matlab进行仿真验证。本发明将ugv的质量设置为m＝22kg，最大牵引力为f
max
＝200n，动摩擦系数为μ＝0.1，重力加速度为g＝9.81m/s2，静摩擦系数为μs＝0.5，非平坦地图模型为：
[0122][0123]
地图设置为100m
×
100m的大小，分辨率是1m。无人车的初始时刻和终端时刻的速度、加速度均设置为0，即v
η0
＝0m/s，v
ηe
＝0m/s，a
η0
＝0m/s2，a
ηe
＝0m/s2，最大速度为v
max
＝2$m/s，最大加速度为a
max
＝2m/s2，运动走廊的宽度为地图分辨率的四倍，即4m，因此相邻运动走廊相交圆形区域的半径为r＝2m。无人车的起始点坐标分别为(19,34)和(65,82)。仿真结果如图4a，图4b，图4c和表1所示，对比方法分别为z*规划算法，基于dijkstra算法的最短路径规划方法dijkstra-d
opt
和能耗最优规划方法dijkstra-e
opt
。
[0124]
表1 不同路径轨迹的关键信息对比
[0125][0126][0127]
本发明说明书中未作详细描述的内容属于本领域专业技术人员公知的现有技术。尽管为了说明本发明的目的，已描述了本发明的示例性实施方式，但是本领域的技术人员将理解，不脱离所附权利要求中公开的发明的范围和精神的情况下，可以在形式和细节上进行各种修改、添加和替换等的改变，而所有这些改变都应属于本发明所附权利要求的保护范围，并且本发明要求保护的产品各个部件和方法中的各个步骤，可以以任意组合的形式组合在一起。因此，对本发明中所公开的实施方式的描述并非为了限制本发明的范围，而是用于描述本发明。相应地，本发明的范围不受以上实施方式的限制，而是由权利要求或其等同物进行限定。