一种基于全输出反馈的车辆系统单调收敛迭代学习控制方法

1.本发明涉及自动控制技术领域，涉及车辆自动驾驶控制，尤其涉及一种基于全输出反馈的车辆系统单调收敛迭代学习控制方法。


背景技术：

2.目前，车辆自动驾驶的相关问题在实际生活中受到了广泛的关注。随着时代的飞速发展，对车辆系统自主控制的精度要求越来越高，在实际生活中，车辆系统的精确模型是未知的，这使得一些传统的控制方法不能满足高精度对期望轨迹实现实时跟踪任务。迭代学习控制方法简单，不需要动态系统的精确数学模型，因此十分适合于对上述车辆系统进行控制，保证车辆系统实现高精度跟踪期望轨迹的目标。
3.但是，在实际生活中，车辆系统对应的系统矩阵往往是随着时间改变的，传统的迭代学习控制方法往往不能使上述具有时变特性的车辆系统的实际输出轨迹单调收敛于期望轨迹，因此具有局限性，不能达到最佳的控制效果。


技术实现要素：

4.为了解决上述现有技术的问题，本发明提出一种基于全输出反馈的车辆系统单调收敛迭代学习控制方法，该方法能够使车辆系统的实际输出轨迹单调收敛于期望轨迹。
5.为了实现上述目的，本发明采用的技术方案是：
6.根据本发明的一个方面，提出了一种基于全输出反馈的车辆系统单调收敛迭代学习控制方法，包括以下步骤：
7.a：设置所述车辆系统的期望轨迹；
8.b：设计全输出反馈迭代学习控制律的迭代学习控制增益矩阵；
9.c：获取所述车辆系统在全输出反馈迭代学习控制律所产生的系统输入驱动下的输入和输出数据，进而计算得到所述车辆系统在当前迭代下的跟踪误差和输出偏差；
10.d：根据所述车辆系统在当前迭代下的控制输入、输出偏差以及迭代学习控制增益矩阵，利用全输出反馈迭代学习控制律更新所述车辆系统下次运行时的控制输入；
11.e：返回至步骤c继续进行，直至完成对期望轨迹的跟踪，即跟踪误差单调收敛到0。
12.进一步地，所述车辆系统具有如下特性：
[0013][0014]
其中，t∈{0,1,
…
,t-1}为运行时刻，t为运行周期，k∈{1,2,
…
}为迭代次数；及分别为所述车辆系统在第k次迭代下t时刻对应的n维状态，q维输入以及p维输出；a(t)，b(t)及c(t)分别为所述车辆系统在t时刻的状态矩阵、输入矩阵和输出矩阵，相互独立；xk(0)＝x0表示系统初始状态可以重置到固定状态x0。
[0015]
进一步地，步骤a具体包括：
[0016]
根据跟踪要求，人为给定期望轨迹，如下：
[0017]
yd(t),t∈{1,2,
…
,t}。
[0018]
进一步地，步骤b具体包括：
[0019]
控制增益γ
t,s
满足下述单调收敛条件：
[0020]
ρ(i
q-c(t+1)b(t)γ
t,t
)《1,t∈{0,1,
…
,t-1}，
[0021]
||i
qt-hγ||
∞
≤1，
[0022]
其中iq是q
×
q单位矩阵，i
qt
是qt
×
qt单位矩阵，ρ(i
q-c(t+1)b(t)γ
t,t
)是矩阵i
q-c(t+1)b(t)γ
t,t
的谱半径，||i
qt-hγ||
∞
是矩阵i
qt-hγ的无穷范数，γ
t,s
是控制增益，t、s分别表示下标，且t、s∈{0，1，
…
，t-1}，
[0023]023]
为迭代学习控制增益矩阵，由控制增益组成。
[0024]
进一步地，步骤c具体包括：
[0025]
根据所述车辆系统在当前迭代下的输出yk(t)以及期望轨迹yd(t)，计算所述车辆系统在当前迭代下的输出偏差ek(t)和在无穷范数意义下的系统输出跟踪误差其中ek(t)＝yd(t)-yk(t)、t∈{1,2,
…
,t}。
[0026]
进一步地，步骤d具体包括：
[0027]
d1：根据所述车辆系统当前迭代下的控制输入、输出偏差以及迭代学习控制增益矩阵确定所述车辆系统下运行时的控制输入：
[0028][0029]
其中，uk(t)为所述车辆系统在第k次迭代中的控制输入，ek(s+1)为所述车辆系统在第k次迭代中的输出偏差，γ
t,s
为所述车辆系统的控制增益,迭代学习控制增益矩阵γ由控制增益γ
t,s
组成。
[0030]
d2：根据所述车辆系统下一次迭代下的控制输入控制所述车辆系统执行下次迭代过程。
[0031]
根据本发明的另一个方面，提出了一种车辆系统装置，具体包括：
[0032]
第一获取模块，用于获取所述车辆系统的期望轨迹；
[0033]
第二获取模块，用于获取所述车辆系统的迭代学习控制增益矩阵；
[0034]
第三获取模块，用于获取在当前迭代中所述车辆系统的跟踪误差和输出偏差；
[0035]
控制模块，用于根据所述车辆系统在当前迭代下的控制输入、输出偏差以及迭代
学习控制增益矩阵更新下次迭代时所述车辆系统的控制输入，控制所述车辆系统，直至跟踪误差单调收敛到0。
[0036]
进一步地，所述控制模块包括：
[0037]
全输出迭代学习控制率子模块：用于根据所述车辆系统当前迭代下的控制输入、输出偏差以及迭代学习控制增益矩阵确定所述车辆系统下次运行时的控制输入：
[0038][0039]
其中，uk(t)为所述车辆系统在第k次迭代中的控制输入，γ
t,s
为所述车辆系统的控制增益，ek(s+1)为所述车辆系统在第k次迭代中的跟踪误差；
[0040]
控制子模块：用于根据所述车辆系统下一次运行时的控制输入控制所述车辆系统执行下一次迭代过程。
[0041]
与现有技术相比，通过本发明提供的基于全输出反馈的车辆系统单调迭代学习控制方法，克服了车辆系统的时变特性的影响，并且使得所述车辆系统的实际输出轨迹单调收敛于期望轨迹，实现了对期望轨迹的跟踪，并且具有较高的精度。
附图说明
[0042]
构成本技术的一部分附图用来提供对本发明的进一步理解，本发明的示意性实施例及其说明用于解释本发明，并不构成对本发明的不当限定，在附图中：
[0043]
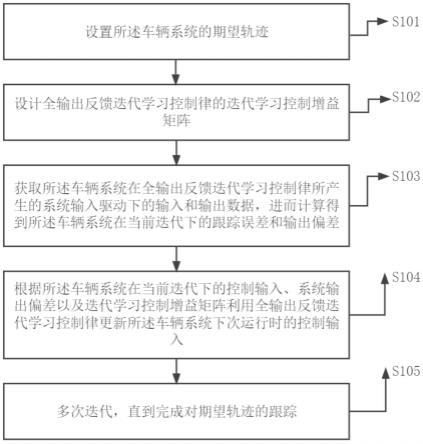
图1为根据本发明一个实施例的基于全输出反馈的车辆系统单调收敛迭代学习控制方法的流程图。
[0044]
图2为车辆系统的跟踪误差沿着迭代轴的动态演变图。
具体实施方式
[0045]
需要说明的是，在不冲突的情况下，本技术中的实施例及实施例中的特征可以相互组合。下面将参考附图并结合实施例来详细说明本发明。
[0046]
为了使本技术领域的人员更好地理解本发明方案，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分的实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都应当属于本发明保护的范围。
[0047]
需要说明的是，本发明的说明书和权利要求书及上述附图中的术语“第一”、“第二”等是用于区别类似的对象，而不必用于描述特定的顺序或先后次序。应该理解这样使用的数据在适当情况下可以互换，以便这里描述的本发明的实施例。此外，术语“包括”和“具有”以及他们的任何变形，意图在于覆盖不排他的包含，例如，包含了一系列步骤或单元的过程、方法、系统、产品或设备不必限于清楚地列出的那些步骤或单元，而是可包括没有清楚地列出的或对于这些过程、方法、产品或设备固有的其它步骤或单元。
[0048]
图1为根据本发明一个实施例的基于全输出反馈的车辆系统单调迭代学习控制方法的流程图，如图1所示，该方法包括以下步骤：
[0049]
步骤s101：设置所述车辆系统的期望轨迹，所述期望轨迹是人为设置的期望运行
路线，为车辆系统最终所期望运行的参考轨迹；
[0050]
具体地，根据跟踪要求，人为给定期望轨迹，如下：
[0051]
yd(t),t∈{1,2,
…
,t}。
[0052]
步骤s102：设计全输出反馈迭代学习控制律的迭代学习控制增益矩阵；
[0053]
所述全输出反馈迭代学习控制率可以使所述车辆系统产生下一次迭代的控制输入，以此控制所述车辆系统；所述迭代学习控制增益矩阵为所述全输出反馈迭代学习控制律的核心部分，用于保证所述全输出反馈迭代学习控制律可以使所述车辆系统跟踪期望轨迹。
[0054]
具体地，针对具有如下时变特性的车辆系统：
[0055][0056]
其中，t∈{0,1,
…
,t-1}为运行时刻，t为运行周期，k∈{1,2,
…
}为迭代次数；及分别为所述车辆系统在第k次迭代下t时刻对应的n维状态，q维输入以及p维输出；a(t)，b(t)及c(t)分别为所述车辆系统在t时刻的状态矩阵、输入矩阵和输出矩阵，相互独立；xk(0)＝x0表示系统初始状态可以重置到固定状态x0。
[0057]
控制增益γ
t,s
满足下述条件：
[0058]
ρ(i
q-c(t+1)b(t)γ
t,t
)《1,t∈{0,1,
…
,t-1}，
[0059]
||i
qt-hγ||
∞
≤1，
[0060]
其中iq是q
×
q单位矩阵，i
qt
是qt
×
qt单位矩阵，ρ(i
q-c(t+1)b(t)γ
t,t
)是矩阵i
q-c(t+1)b(t)γ
t,t
的谱半径，||i
qt-hγ||
∞
是矩阵i
qt-hγ的无穷范数，γ
t,s
控制增益，t、s分别表示下标，且t、s∈{0，1，
…
，t-1}，
[0061][0061]
为迭代学习控制增益矩阵，由控制增益组成。
[0062]
步骤s103：获取所述车辆系统在全输出反馈迭代学习控制律所产生的系统输入驱动下的输入和输出数据，进而计算得到所述车辆系统在当前迭代下的跟踪误差和输出偏差；
[0063]
具体地，所述全输出反馈迭代学习控制律所产生的系统输入是指上一次迭代的系统输入，即u
k-1
(t)；所述系统输入驱动下的输入数据指当前迭代的系统输入，即uk(t)；所述系统输入驱动下的输出数据即为当前迭代下的输出yk(t)；上述数据可在车辆系统中安装相应的位置传感器装置获取。
[0064]
根据所述车辆系统在当前迭代下的输出yk(t)以及期望轨迹yd(t)，计算所述车辆系统在当前迭代下的输出偏差ek(t)和在无穷范数意义下的系统输出跟踪误差其中ek(t)＝yd(t)-yk(t)、t∈{1,2,
…
,t}。
[0065]
步骤s104：根据所述车辆系统在当前迭代下的控制输入、输出偏差以及迭代学习控制增益矩阵利用全输出反馈迭代学习控制律更新所述车辆系统下次运行时的控制输入；
[0066]
具体地，首先确定所述车辆系统的迭代学习控制率，然后根据确定的控制率更新下一次迭代的控制输入，进而控制所述车辆车辆系统。在本发明的实施例中，根据所述车辆系统当前迭代下的控制输入、输出偏差以及迭代学习控制增益矩阵确定所述车辆系统下运行时的控制输入：
[0067][0068]
其中，uk(t)为所述车辆系统在第k次迭代中的控制输入，可由安装在车辆系统上的传感器装置获取，γ
t,s
为所述车辆系统的控制增益，ek(s+1)为所述车辆系统在第k次迭代中的输出偏差；表示每次更新都需要利用所有时刻的输出偏差信息，可以提高学习性能。
[0069]
根据所述车辆系统下一次迭代下的控制输入控制所述车辆系统执行下次迭代过程。
[0070]
步骤s105：返回至步骤s103继续进行，直至完成对期望轨迹的跟踪，即跟踪误差单调收敛到0。
[0071]
单调收敛是指跟踪误差||ek(t)||
∞
随着迭代次数k的增加而减少，当迭代次数k趋于无穷大时，跟踪误差||ek(t)||
∞
趋于0，单调收敛可以防止控制过程中产生超调，超调量过大可能会对系统硬件产生破坏。
[0072]
对期望轨迹实现跟踪可以使所述汽车系统在不需要人为控制的情况下，由给定的迭代学习控制率控制所述汽车按照给定的路线进行移动。
[0073]
以下结合实施例对本发明的基于全输出反馈的车辆系统单调收敛迭代学习控制方法进行详细描述，但不能将其理解为对本发明保护范围的限定。
[0074]
实施例1：
[0075]
考虑具有如下时变特性的车辆系统：
[0076][0077]
其中系统矩阵为：
[0078][0079]
考虑运行周期为t＝20，同时选择车辆系统运行的初始状态为x0＝[0，0，0]
t
，初始
输入为u0(t)＝[0，0]
t
，执行初次迭代k＝0；
[0080]
s101：确定车辆系统的期望轨迹为yd(t)＝[sin(0.3t)e-0.05t
，2sin(0.3t)e-0.05t
]
t
，t∈{1，2，
…
，20}。
[0081]
s102：设计全输出反馈迭代学习控制律的迭代学习控制增益矩阵；
[0082]
计算得矩阵
[0083]
选择迭代学习控制增益矩阵：
[0084][0085]
由迭代学习控制增益矩阵γ可以得到控制增益γ
t,s
，即
[0086][0087]
且所选的迭代学习控制增益矩阵以及控制增益均满足以下条件：
[0088]
ρ(i
q-c(t+1)b(t)γ
t,t
)《1,t∈{0,1,
…
,t-1}，
[0089]
||i
qt-hγ||
∞
≤1，
[0090]
其中iq是q
×
q单位矩阵，i
qt
是qt
×
qt单位矩阵，ρ(i
q-c(t+1)b(t)γ
t,t
)是矩阵i
q-c(t+1)b(t)γ
t,t
的谱半径，||i
qt-hγ||
∞
是矩阵i
qt-hγ的无穷范数。
[0091]
s103：获取所述车辆系统在全输出反馈迭代学习控制律所产生的系统输入驱动下的输入和输出数据，分别为uk(t)，t∈{0，1，
…
，19}，和yk(t)，t∈{1，2，...，20}，计算出当前迭代下的输出偏差ek(t)＝yd(t)-yk(t)，t∈{1,2,
…
,t}和在无穷范数意义下的系统输出跟踪误差
[0092]
s104：根据所述车辆系统在当前迭代下的控制输入、输出偏差以及迭代学习控制增益矩阵利用全输出反馈迭代学习控制律更新所述车辆系统下次运行时的控制输入；具体包括如下步骤：
[0093]
首先确定所述车辆系统的迭代学习控制率，根据所述车辆系统当前迭代下的控制输入、输出偏差以及迭代学习控制增益矩阵确定所述车辆系统下运行时的控制输入：
[0094][0095]
其中，uk(t)为所述车辆系统在第k次迭代中的控制输入，γ
t,s
为所述车辆系统的控制增益，ek(s+1)为所述车辆系统在第k次迭代中的输出偏差；
[0096]
根据所述车辆系统下一次迭代下的控制输入控制所述车辆系统执行下次迭代过程。
[0097]
s105:返回至步骤s103继续进行，直至完成对期望轨迹的跟踪，即跟踪误差单调收敛到0。
[0098]
图2中展示了在30次迭代后，车辆系统的跟踪误差单调收敛到0。该图说明了车辆系统可以完美跟踪期望输出轨迹，且精度较高。因此根据本发明提供的基于全输出反馈的车辆系统单调收敛迭代学习控制方法，可以克服车辆系统的时变特性影响，对于任意给定的期望轨迹，所述迭代学习控制方法可以使所述车辆系统的实际输出轨迹单调收敛于期望轨迹，且控制精度较高。
[0099]
以上的具体实施方式，对本发明的目的、技术方案和有益效果进行了进一步详细说明，所应理解的是，以上仅为本发明的具体实施方式而已，并不用于限定本发明的保护范围，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。