基于模型参考自适应控制的仿人机器人变负载站立方法

1.本发明涉及仿人机器人运动控制领域，尤其涉及一种基于模型参考自适应控制的仿人机器人变负载站立方法。


背景技术：

2.仿人机器人在近几十年蓬勃发展，尤其是在步态生成和平衡控制领域发展迅速，已经取得了不错的成果。但是真正的应用仍然还有很大的距离，许多关键问题仍然亟待解决。目前仿人机器人的研究经常忽视其负载能力的研究，针对搬运、抬举重物这些常见任务所需的载荷重力补偿问题研究较少。载荷重力补偿需要考虑的问题主要有抵御关节偏移和变负载补偿能力。其中，关节偏移指仿人机器人在载荷重力作用下实际关节位置、速度与关节位置、速度指令之间的差值，以及由此差值造成的机器人整体姿态偏移；变负载补偿能力指面对未知负载，或者负载大小变化的情况下，补偿重力载荷，抵御关节偏移的能力。变负载补偿能力是机器人负载能力的高级形式，是仿人机器人完成搬运、抬举重物这些常见任务的基础，对仿人机器人实际应用具有重大意义。
3.上述机器人的负载能力取决于关节驱动方式和机械设计结构，当载荷重力足够大时，机器人关节会产生偏移并导致姿态控制误差。特别地，对于采用电机驱动的仿人机器人，受限于较小的关节驱动能力，以上问题尤为显著。实际上，通过采取适当的控制策略，充分发挥关节驱动能力，可以有效提升负载能力。目前的重力载荷补偿策略有增加关节的刚性和在控制器中增加积分器两种。仅增加关节的刚性虽然减少了抬举任务时位置的偏移，却牺牲了机器人的顺应性；仅使用积分器虽能适应机器人重力载荷的变化，但积分器生效需要时间，无法满足一些高动态任务的要求。由此可见，现有技术这些方法虽然可以解决重力载荷变化和模型误差问题，但是他们是针对特定情境下的特定问题所设计，并非多连杆系统重力补偿问题的系统或通用方法。


技术实现要素：

4.针对现有技术的不足，本发明提出了仿人机器人在双腿并排站立时的变负载站立控制方法。本发明基于仿人机器人在双腿并排站立时的简化三连杆模型，推导动力学方程；设计模型参考自适应控制算法，通过施加适当的前馈力矩，提供支撑负载重力所需的关节力矩。由于自适应控制方法可以根据关节控制误差实时调整动力学参数，本发明的仿人机器人能够在支撑未知负载情况下，维持较高的关节控制精度。本发明在常见的双足机器人或仿人机器人平台上具有一定的通用性，对于不同类型的负载任务如搬运、托举重物等均有较好的适用性。
5.本发明的目的通过以下技术方案实现：
6.一种基于模型参考自适应控制的仿人机器人变负载站立方法，包括以下步骤：
7.步骤一：构建简化的仿人机器人动力学模型，推导动力学方程，具体通过以下方式实现：
8.将双腿并排站立的仿人机器人，等效简化为三连杆模型；基于拉格朗日方程，推导所述三连杆模型的动力学方程；对所述动力学方程的形式进行转换，得到与动力学参数相关的三连杆模型关节力矩表达式；
9.步骤二：设计仿人机器人双腿并排站立下的模型参考自适应控制算法，具体通过以下方式实现：
10.将期望角度、期望角速度、期望角加速度代入所述与动力学参数相关的三连杆模型关节力矩表达式，计算得到关节力矩的估计值，将其作为前馈力矩，施加在pd控制器的输出端；同时计算得到参考关节角速度；
11.根据所述前馈力矩和pd控制器的微分系数，计算所述三连杆模型的关节力矩，将其作为控制输入，输入到所述仿人机器人的控制系统中，输出得到所述仿人机器人各关节的实际角度和角速度；
12.根据所述仿人机器人各关节的实际角速度和所述参考关节角速度，计算得到广义误差，再由广义误差计算得到动力学参数估计值的更新率，更新动力学参数，获得更准确的前馈力矩，直至消除关节角度、角速度的控制误差。
13.进一步地，所述基于拉格朗日方程推导三连杆模型的动力学方程具体通过以下方式实现：
14.多连杆系统中的拉格朗日方程为：
[0015][0016]
式中，θ为关节角度；为关节角速度；τ为关节力矩；为系统动能；v(θ,t)为重力势能；
[0017]
所述三连杆模型从上到下包括：躯干连杆、髋关节、大腿连杆、膝关节、小腿连杆、踝关节、足连杆；所述髋关节为连接所述躯干连杆和所述大腿连杆的结构，所述膝关节为连接所述大腿连杆和所述小腿连杆的结构，所述踝关节为连接所述小腿连杆和所述足连杆的结构，所述髋关节、踝关节均能进行多方向的转动；
[0018]
根据仿人机器人各连杆的物理参数，计算得到所述三连杆模型中各连杆的动能、重力势能，代入式(1)并整理得到：
[0019][0020]
式中，h(θ)是实对称的惯性矩阵；为关节角加速度；是与向心力和科里奥利力相关的矩阵；g(θ)是由重力决定的矩阵，h(θ)、g(θ)的具体表达式如下：
[0021][0022][0023]
[0024]
式中，θ1为所述小腿连杆与竖直方向的夹角，θ2为所述大腿连杆与所述小腿连杆的夹角，θ3为所述躯干连杆与所述大腿连杆的夹角；为所述踝关节在y方向的关节角速度，所述y方向为所述仿人机器人双腿并排站立时，指向身体左侧的方向；为所述膝关节在y方向的关节角速度，为所述髋关节在y方向的关节角速度；a1,2,3,4,5,6,7,8,9均为动力学参数，其具体表达式如下：
[0025][0026]
式中，m1表示所述小腿连杆的质量，m2表示所述大腿连杆的质量，m3表示所述躯干连杆的质量；i1表示所述小腿连杆绕其质心的转动惯量，i2表示所述大腿连杆绕其质心的转动惯量，i3表示所述躯干连杆绕其质心的转动惯量；l1表示所述小腿连杆的长度，l2表示所述大腿连杆的长度；d1表示所述小腿连杆质心与所述踝关节间的距离，d2表示所述大腿连杆质心与所述膝关节间的距离，d3表示所述躯干连杆质心与所述髋关节之间的距离；g表示重力加速度。
[0027]
进一步地，所述对动力学方程的形式进行转换，具体通过以下方式实现：
[0028]
将向量分解为矩阵与关节角速度向量的乘积形式，所述矩阵满足与h(θ)的导数构成的矩阵为反对称矩阵，将矩阵与关节角速度向量代入式(2)得到：
[0029][0030]
式中，矩阵的具体表达式如下：
[0031][0032]
利用动力学参数的线性性质，将关节力矩τ分解为：
[0033]
[0034]
式中，a为动力学参数，所述a1,a2,a3,a4,a5,a6,a7,a8,a9为a的分量，a与机器人各连杆机械参数相关；y为回归矩阵，只与机器人运动状态相关，y的具体表达式如下：
[0035][0036][0037]
式中，表示所述踝关节在y方向的角加速度，表示所述膝关节在y方向的角加速度，表示所述髋关节在y方向的角加速度。
[0038]
进一步地，所述模型参考自适应控制算法具体通过以下方式实现：
[0039]
根据所述与动力学参数相关的三连杆模型关节力矩表达式，计算得到关节力矩的估计值，将其作为前馈力矩，所述前馈力矩的表达式为：
[0040][0041]
式中，为动力学参数的估计值，为h(θ)的估计值，表示参考关节角加速度，为的估计值，为g(θ)的估计值；
[0042]
将所述前馈力矩施加在pd控制器的输出端，结合所述pd控制器的微分系数，计算所述三连杆模型的关节力矩
[0043][0044]
式中，d表示pd控制器的微分系数，为正对角矩阵，需要手动调节；s表示广义误差，
[0045]ds为比例-微分项，其作用等价于所述pd控制器；
[0046]
设计参数更新律，根据广义误差s更新动力学参数，获得更准确的前馈力矩参数更新律的表达式如下：
[0047][0048][0049][0050][0051]
式中，为动力学参数估计值的更新率；γ表示参数更新速率，为正对角矩阵，需手
动调节；表示关节角速度误差；λ表示所述pd控制器的比例系数，为正对角矩阵，需手动调节；表示关节角度误差；表示实际关节角速度；表示参考关节角速度，为参考输出；表示期望关节角速度；θ表示实际关节角度，θd表示期望关节角度。
[0052]
进一步地，所述仿人机器人各连杆的物理参数包括：仿人机器人各连杆质量、长度、质心位置、惯性张量。
[0053]
本发明的有益效果是：
[0054]
(1)现有的仿人机器人重力负载补偿方案，无论是增加关节的刚性或在控制器中增加一个积分器，均属于反馈控制，无法在很短的时间内获得高精度的关节控制效果；本发明使用了前馈控制，通过双腿并排站立时对应的三连杆模型动力学方程计算支撑重力负载所需的关节力矩，将其直接加在pd控制器的输出端，既缩短了控制时间，又能保证关节控制精度。
[0055]
(2)为适应负载变化，本发明设计了模型参考自适应控制算法，通过调整动力学参数，改变动力学方程计算出的关节力矩，保证关节控制的精度。
[0056]
(3)本发明在常见的双足机器人或仿人机器人平台上具有一定的通用性，对于不同类型的负载任务如搬运、托举重物等均有较好的适用性。
附图说明
[0057]
图1是仿人机器人双腿并排站立时简化等效的三连杆模型图。
[0058]
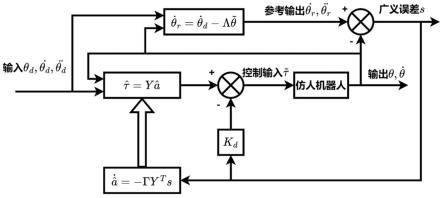
图2是仿人机器人的模型参考自适应控制流程框图。
[0059]
图3是仿人机器人突加重力负载时质心高度控制效果图。
[0060]
图中，躯干连杆1、躯干连杆质心2、髋关节3、大腿连杆4、大腿连杆质心5、膝关节6、小腿连杆7、小腿连杆质心8、踝关节9。
具体实施方式
[0061]
下面根据附图和优选实施例详细描述本发明，本发明的目的和效果将变得更加明白，以下结合附图和实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。
[0062]
本发明基于模型参考自适应控制的仿人机器人变负载站立方法，具体通过如下步骤实现：
[0063]
步骤一：构建简化的仿人机器人动力学模型，推导动力学方程。
[0064]
基于拉格朗日方程，将双腿并排站立的仿人机器人，简化等效为如图1所示的三连杆模型，并推导其动力学方程。
[0065]
如图1所示，为仿人机器人双腿并排站立时简化等效的三连杆模型图，仿人机器人的一条腿从上到下包括：躯干连杆1、髋关节3、大腿连杆4、膝关节6、小腿连杆7、踝关节9、足连杆。其中髋关节3为连接躯干连杆1和大腿连杆4的结构，可进行多个方向的转动；膝关节6为连接大腿连杆4和小腿连杆7的结构；踝关节9为连接小腿连杆7和足连杆的结构，可进行多个方向的转动。在本实施例中，各关节的关节角度、角速度、角加速度特指在y方向上的角度、角速度、角加速度，y方向为仿人机器人双腿并排站立时，指向身体左侧的方向。取各连
杆的质心分别为躯干连杆质心2、大腿连杆质心5、小腿连杆质心8；各连杆质心到各相邻关节(向下)的距离分别为d1、d2、d3，各连杆长度分别为l1、l2、l3，各关节角分别为θ1、θ2、θ3。
[0066]
多连杆系统中的拉格朗日方程为：
[0067][0068]
式中，θ为关节角度；为关节角速度；τ为关节力矩；为系统动能；v(θ,t)为重力势能。
[0069]
根据仿人机器人各连杆质量、长度、质心位置、惯性张量等参数，计算得到三连杆模型中各连杆的动能、重力势能，代入式(1)并整理得到三连杆模型的动力学方程：
[0070][0071]
式中，h(θ)是实对称的惯性矩阵；为关节角加速度；是与向心力和科里奥利力相关的矩阵；g(θ)是由重力决定的矩阵，h(θ)、g(θ)的具体表达式如下：
[0072][0073][0074][0075]
式中，θ1为小腿连杆7与竖直方向的夹角，θ2为大腿连杆4与小腿连杆7的夹角，θ3为躯干连杆1与大腿连杆4的夹角；为踝关节9在y方向的关节角速度，为膝关节6在y方向的关节角速度，为髋关节3在y方向的关节角速度；a1,a2,a3,a4,a5,a6,a7,a8,a9均为动力学参数，其具体表达式如下：
[0076][0077]
式中，m1表示小腿连杆7的质量，m2表示大腿连杆4的质量，m3表示躯干连杆1的质量；i1表示小腿连杆7绕其质心的转动惯量，i2表示大腿连杆4绕其质心的转动惯量，i3表示躯干连杆1绕其质心的转动惯量；l1表示小腿连杆7的长度，l2表示大腿连杆4的长度；d1表示小腿连杆质心8与踝关节9间的距离，d2表示大腿连杆质心5与膝关节6间的距离，d3表示躯干连杆质心2与髋关节3之间的距离；g表示重力加速度。
[0078]
步骤二：对动力学方程的形式进行转换，定义动力学参数。
[0079]
为了便于模型参考自适应控制方法的施加，需要对动力学方程的形式进行转换，将向量分解为矩阵与关节角速度向量的乘积形式，其中矩阵满足与h(θ)的导数构成的矩阵为反对称矩阵，将矩阵与关节角速度向量代入式(2)得到：
[0080][0081]
式中，矩阵的具体表达式如下：
[0082][0083]
利用动力学参数的线性性质，将关节力矩τ分解为：
[0084][0085]
式中，a为动力学参数，a1,a2,a3,a4,a5,a6,a7,a8,a9为其分量，a与机器人各连杆质量、长度、质心位置等机械参数相关；y为回归矩阵，只与机器人运动状态(各关节角度、角速度、角加速度)相关，y的具体表达式如下：
[0086][0087]
式中，表示踝关节9在y方向的角加速度，表示膝关节6在y方向的角加速度，表示髋关节3在y方向的角加速度；y
14
、y
24
、y
15
、y
25
、y
35
、y
16
、y
26
、y
36
的具体表达式如下：
[0088]
[0089]
步骤三：设计模型参考自适应控制算法，调整动力学参数以适应负载变化。
[0090]
如图2所示，为仿人机器人的模型参考自适应控制流程框图。机器人搬运、托举重物时，负载的变化可以视为机器人自身动力学参数的变化，模型参考自适应算法根据广义误差调整动力学参数估计值，改变前馈力矩，从而保证关节控制精度。具体流程如下：
[0091]
(3.1)模型参考自适应控制算法以期望关节角度θd、期望关节角速度期望关节角加速度作为输入，根据与动力学参数相关的三连杆模型关节力矩表达式计算得到关节力矩的估计值，将其作为前馈力矩并将其施加在传统pd控制器的输出端。
[0092][0093]
式中，为动力学参数的估计值，为h(θ)的估计值，表示参考关节角加速度，为的估计值；表示参考关节角速度，其具体表达式如下式(16)所示；为g(θ)的估计值。
[0094]
(3.2)设计控制律，根据前馈力矩和pd控制器的微分系数kd计算得到关节力矩将其作为控制输入，输入到仿人机器人控制系统中，输出得到仿人机器人各关节的实际角度θ和角速度
[0095][0096]
式中，为关节力矩，是控制量；kd表示pd控制器的微分系数，为正对角矩阵，需要手动调节；s表示广义误差，其具体表达式如下式(15)所示；-kds为比例-微分项，其作用等价于pd控制器。
[0097]
(3.3)设计参数更新律，根据实际关节角速度和参考关节角速度得到广义误差s，再由广义误差s计算动力学参数估计值的更新率更新动力学参数，获得更准确的前馈力矩，直至消除关节角度、角速度的控制误差。
[0098]
参数更新律的表达式如下：
[0099][0100][0101][0102][0103]
式中，为动力学参数估计值的更新率；γ表示参数更新速率，为正对角矩阵，需手动调节；s表示广义误差；表示关节角速度误差；λ表示pd控制器的比例系数，为正对角矩阵，需手动调节；表示关节角度误差；表示实际关节角速度；表示参考关节角速度，为参考输出；表示期望关节角速度；θ表示实际关节角度，θd表示期望关节角度。
[0104]
基于李雅普诺夫稳定性理论证明此模型参考自适应控制系统的稳定性。选择李雅普诺夫函数为：
[0105]
[0106]
式中，为动力学参数估计误差。
[0107]
由于h(θ)为惯性矩阵，则多连杆系统的动能为：
[0108][0109]
系统的动能总是大于零，因此有所以惯性矩阵h(θ)是正定的；由于γ是人为给定的正对角阵，是正定的，因此v(t)是正定的，对其求导得到：
[0110][0111]
式中，为s的导数，为h的导数，为的导数。
[0112]
由于是反对称矩阵，所以变换得到：
[0113][0114]
将式(21)带入式(20)得：
[0115][0116]
因此是负定的。由李雅普诺夫稳定性理论可知，当t
→
∞时，s
→
0，考虑广义误差定义式当s
→
0时，从而从理论层面证明了系统的全局稳定性，关节角度、关节角速度的控制误差及动力学参数估计误差的收敛性。
[0117]
下面进行仿人机器人变负载站立调试。
[0118]
(1)获取仿人机器人各连杆质量、长度、质心位置、惯性张量等参数，作为动力学参数的初始值；将初始值输入模型参考自适应控制算法中，调整参数更新速率γ、微分系数kd、比例系数λ，使负载变化时，模型参考自适应控制算法能够及时调整动力学参数，消除关节控制误差。
[0119]
(2)改变仿人机器人的负载，验证对仿人机器人的变负载站立控制是否达到预期效果。为验证该模型参考自适应控制算法的控制效果，利用能简化为三连杆模型的仿人机器人在动力学仿真平台进行仿真验证。
[0120]
本实施例中利用“悟空
‑ⅲ”
urdf模型在raisim平台进行仿真验证，结果如图3所示。仿人机器人“悟空
‑ⅲ”
直立身高1.409m，重55.0307kg；在t＝4s时向其质心施加300n竖直向下的力，观察质心高度变化可知：突加负载后，质心高度在0.5s内恢复，且最大偏移量小于0.012m，说明模型参考自适应方法能够在较大的重力载荷下保证较好的姿态维持效
果。
[0121]
本发明基于拉格朗日方程，将双腿并排站立的仿人机器人，简化等效为三连杆模型，并推导其动力学方程；将关节角度、角速度作为被控对象，关节力矩作为控制输入，动力学方程中的动力学参数作为可调参数，构建模型参考自适应控制框架，结合基于pd控制的传统反馈控制和基于动力学方程的前馈控制，获得未知负载下高精度的关节控制效果。
[0122]
本领域普通技术人员可以理解，以上所述仅为发明的优选实例而已，并不用于限制发明，尽管参照前述实例对发明进行了详细的说明，对于本领域的技术人员来说，其依然可以对前述各实例记载的技术方案进行修改，或者对其中部分技术特征进行等同替换。凡在发明的精神和原则之内，所做的修改、等同替换等均应包含在发明的保护范围之内。