一种基于有限时间指令滤波反步法的船舶动力定位控制系统及方法

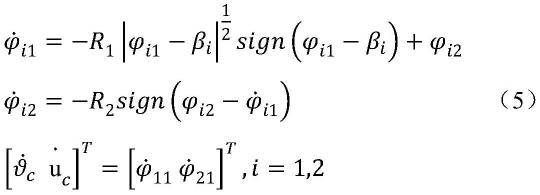
本发明涉及一种船舶动力定位有限时间指令滤波反步控制系统，本发明也涉及一种船舶动力定位有限时间指令滤波反步控制方法。


背景技术：

随着对深海资源的不断开发，对船舶定位方式的研究也显得尤为重要。其中，动力定位系统就是研究者们重点研究的一种定位方式。在动力定位(dynamic positioning)系统中，控制系统是其最重要的组成部分，因此对dp的非线性控制引起了研究者们的关注。常用的dp控制方法主要有：pid控制，lqr控制，模型预测控制，鲁棒自适应控制等。其中鲁棒自适应控制是近来研究的热点，主要的自适应控制方法有滑模控制、自适应反步法等。中国专利cn109460043a提出了一种基于多模态非奇异终端滑模船舶航迹自抗扰控制方法，该专利利用状态观测器，使其内部函数可以实时在线性、非线性函数之间进行切换；设计了可切换的分段滑模面，并引入了一种新型双幂次趋近律，以达到快速趋近目的，最后利用此分段滑模面设计了可切换误差反馈控制律。滑模控制法具有较好的鲁棒性和较快的收敛性，但是它只能处理特定的系统，不具有通用性。与该方法不同的是，本发明主要针对执行机构下船舶运动中模型不确定、未建模动态项和和推进器动态特性采用有限时间指令滤波法对dp系统进行研究。


技术实现要素：

本发明的目的在于提供一种抗干扰能力好、定位精度高且在有限时间内使执行机构快速发出指令以达到较好控制效果的基于神经网络的有限时间指令滤波反步定位控制系统。本发明的目的还在于提供一种基于神经网络的有限时间指令滤波反步定位控制方法。本发明基于神经网络的有限时间指令滤波反步定位控制系统，包括显控计算机(1)，有限时间指令滤波反步控制器(2)，rbf神经网络误差补偿系统(3)，推进系统(4)，动力定位船舶(5)，传感器系统(6)，其特征是：传感器系统(6)实时采集动力定位船舶(5)的位姿信息η，并将采样得到的位姿信息传递给显控计算机(1)、有限时间指令滤波反步控制器(2)和rbf神经网络补偿系统(3)；显控计算机(1)实时显示船舶的实际位姿信息并将期望位置阶跃信号ηd传递给有限时间指令滤波反步控制器(2)；有限时间指令滤波控制器(2)构造虚拟信号βi和虚拟控制量μc对期望位置阶跃信号ηd进行计算得到各跟踪误差ηe，μe构造误差补偿信号ξ1，ξ2，ξ3并传递给各跟踪误差补偿向量系统输出各跟踪误差补偿向量v1，v2，v3；rbf神经网络补偿系统(3)对非线性函数f(η，θ)进行逼近，针对控制输入误差θ进行rbf逼近，得到自适应更新率并传递给有限时间指令滤波控制器(2)；自适应更新率和虚拟信号βi进行有限时间滤波控制，得到推进系统(4)在推进器动态特性下的控制指令τc；推进系统(4)根据有限时间指令滤波反步控制器(2)输出的控制指令τc对动力定位船舶(5)进
行控制并对rbf神经网络误差补偿系统(3)反馈，使得船舶运动到期望位置。本发明的基于神经网络的有限时间指令滤波反步定位控制方法为：(1)传感器系统(6)实时采集动力定位船舶(5)的位姿信息η，并将采样得到的位姿信息传递给显控计算机(1)、有限时间指令滤波反步控制器(2)和rbf神经网络补偿系统(3)；(2)显控计算机(1)实时显示船舶的实际位姿信息并将期望位置阶跃信号ηd传递给有限时间指令滤波反步控制器(2)；(3)有限时间指令滤波控制器(2)构造虚拟信号βi和虚拟控制量μc对期望位置阶跃信号ηd进行计算得到各跟踪误差ηe，μe构造误差补偿信号ξ1，ξ2，ξ3并传递给各跟踪误差补偿向量系统输出各跟踪误差补偿向量ν1，ν2，ν3；(4)rbf神经网络补偿系统(3)对非线性函数f(η，θ)进行逼近，针对控制输入误差θ进行rbf逼近，得到自适应更新率并传递给有限时间指令滤波控制器(2)；(5)自适应更新率和虚拟信号βi进行有限时间滤波控制，得到推进系统(4)在推进器动态特性下的控制指令τc；(6)推进系统(4)根据有限时间指令滤波反步控制器(2)输出的控制指令τc对动力定位船舶(5)进行控制并对rbf神经网络误差补偿系统(3)反馈，使得船舶运动到期望位置。本发明可提高船舶动力定位系统的抗干扰能力和定位精度，在考虑模型不确定、未建模动态项和和推进器动态特性情况下能够达到较好的控制效果。
附图说明
图1是基于神经网络的有限时间滤波反步定位控制系统总体结构图。
具体实施方式
本发明基于神经网络的有限时间滤波反步定位控制系统，包括显控计算机(1)，有限时间指令滤波反步控制器(2)，rbf神经网络误差补偿系统(3)，推进系统(4)，动力定位船舶(5)，传感器系统(6)，其特征是：传感器系统(6)实时采集动力定位船舶(5)的位姿信息η，并将采样得到的位姿信息传递给显控计算机(1)、有限时间指令滤波反步控制器(2)和rbf神经网络补偿系统(3)；显控计算机(1)实时显示船舶的实际位姿信息并将期望位置阶跃信号ηd传递给有限时间指令滤波反步控制器(2)；有限时间指令滤波控制器(2)构造虚拟信号βi和虚拟控制量μc对期望位置阶跃信号ηd进行计算得到各跟踪误差ηe，μe构造误差补偿信号ξ1，ξ2，ξ3并传递给各跟踪误差补偿向量系统输出各跟踪误差补偿向量ν1，ν2，ν3；rbf神经网络补偿系统(3)对非线性函数f(η，θ)进行逼近，针对控制输入误差θ进行rbf逼近，得到自适应更新率并传递给有限时间指令滤波控制器(2)；自适应更新率和虚拟信号βi进行有限时间滤波控制，得到推进系统(4)在推进器动态特性下的控制指令τc；推进系统(4)根据有限时间指令滤波反步控制器(2)输出的控制指令τc对动力定位船舶(5)进行控制并对rbf神经网络误差补偿系统(3)反馈，使得船舶运动到期望位置。下面对本发明的基于神经网络的有限时间滤波反步定位控制方法做更详细的说明：
分别建立每一艘跟随船舶的运动学模型和动力学模型。其中η＝[x y ψ]
t
是大地坐标系下船舶的位置和艏向；υ＝[u v r]
t
是船体坐标系下船舶的速度向量；r是旋转矩阵且m是惯性质量矩阵；c(υ)是科里奥利及向心力矩阵；d(υ)是阻尼矩阵；τ是推进系统产生的力及力矩；d(t)表示未知干扰，其中包括风、浪和海流产生的海洋干扰；ω表示系统的未建模动态和误差且在控制器设计中很有必要考虑推进器的惯性特性以消除控制指令滞后对系统产生的影响。我们可以将推进器考虑为一个一阶惯性环节，其模型可以表示为：其中：a和b为对角阵；τc为控制指令。为了便于控制器设计，首先我们需要对公式(1)和(2)进行变形。令令令且则可以得到：其中定义各跟踪误差为其中ηd是提前设定的期望位置和艏向；是由下面的有限时间指令滤波器产生的虚拟控制量。此滤波器与传统的滤波器相比可以更快的逼近虚拟控制量的微分信号。其中βi是滤波器输入，稍后将对其进行设计。
定义各跟踪误差的补偿向量为:其中ξ1,ξ2,ξ3是误差补偿信号并定义为其中bi,ci,γ是正实数且0＜γ＜1，βi(i＝1,2,3)是虚拟信号，并构建为其中sig
γ
(νi)＝[|ν
i1
|
γ
sgn(ν
i1
),|ν
i2
|
γ
sgn(ν
i2
),|ν
i3
|
γ
sgn(ν
i3
)]
t
,i＝1,2,3引入自适应神经网络系统来对中的未知模型参数进行估计。采用rbf神经网络对非线性函数进行逼近，神经网络输出可以表示为：fi(x)＝w
fit
φ
fi
(x)
ꢀꢀꢀ
(9)根据逼近原理，对于紧集上的任意x，rbf的输出能够以任意精度近似逼f(x)，即：其中是理想权值向量ε
fi
是逼近误差，并且存在正常数δf，使得并且对于是高斯函数，ej＝[c
j1
,c
j2
,
…
,c
jm
]
t
是第i个神经元高斯函数的中心向量，di是高斯函数的基宽。于是β2可以重新写为其中定义θ＝max{‖w
f1
‖2,‖w
f2
‖2,‖w
f3
‖2}，我们可以选择的自适应更新率为
对于系统(1)和(2)我们可以选择有限时间指令滤波器(5)、误差补偿系统(7)、虚拟控制信号(8)和(11)以及(8)中的控制律和自适应更新率(12)，使得(4)中的跟踪误差、(6)中的跟踪误差补偿向量和自适应神经网络系统对非线性函数的估计误差有限时间收敛。根据(4)，对跟踪误差进行求导可得对补偿系统的求导，并将(7)和(8)代入其中，我们可以得到我们选择如下的lyapunov函数：考虑(14)，对其求导根据young’s不等式，我们可以得到下列不等式s不等式，我们可以得到下列不等式同时根据定理，我们可以得到下列不等式同时根据定理，我们可以得到下列不等式将(12)，(17)，(18)，(19)和(20)代入(16)可得
下面分两种情况来讨论：(1)如果我们可以得到下面的不等式(2)如果则我们可以得到不等式：
[0042]
因此，基于以上两点的讨论，我们可以得到其中其中和于是我们可以得到下列不等式：由引理1，我们可以得到以下结论：补偿误差v1,v2,v3在有限时间
内收敛于区域由公式(10)的定义，我们知道如果证明ξi是有限时间有界的，则(6)中的跟踪误差可以有限时间内收敛于原点附近。下面我们来证明误差补偿系统是有限时间有界的，首先选择下面的lyapunov函数对其求导可得根据引理，我们可以知道在有限时间内实现所以我们有其中只要选择合适的l0使得则ξi是有限时间稳定的。