一种基于储能系统的Buck电路自适应动态面控制方法与流程

本发明涉及电力负荷控制领域，特别涉及一种基于储能系统的buck电路自适应动态面控制方法。

背景技术：

1、随着电力电子技术的高速发展，电子设备渗入到人们生活的各个方面，在医疗器械、军工设备和农业生产等更多领域都有着重要地位。其中电力电子转换器，尤其是dc/dc转换器已广泛应用于不同的工业领域。在转换器输入电压和负载不确定的情况下保持dc/dc转换器输出电压的稳定具有多种用途，例如应用于通信设备、计算机和工业控制电子设备的适配器等。因此，以提供稳定直流输出电压为目标的dc/dc转换器得到了迅速的发展。

2、buck电路是电力电子系统中dc/dc变换器的核心构成部分，其工作状态有强烈的非线性特点，其开关的高频切换，更是使得工作状态具有时延性，在某些电路参数条件和初始状态下，buck电路有很多非线性现象，上述情况都会导致dc/dc变换器发生故障使得设备无法正常运行，如果不采取任何补救措施，则这些组件的任何故障都可能导致严重损坏，进而使整个系统瘫痪。传统的电压调节控制方法已经不能满足各个领域技术应用的需求，考虑如何利用高效率的控制策略来改善dc/dc变换器的控制性能，提升应对非最小相位系统输入电压或负载变化时稳定输出电压的能力，成为了研究buck电路控制策略的核心问题。

技术实现思路

1、为克服现有技术的不足，本发明的目的是提供一种基于储能系统的buck电路自适应动态面控制方法，采用性能函数、误差转换函数和引入有限覆盖引理的神经网络系统相结合的buck电路自适应动态面控制方法，可有效补偿传感器测量过程中产生的时间延迟，保证闭环系统中所有信号半全局一致终有界，通过调整控制器参数，跟踪误差可以收敛到任意小的残集内，实现稳定buck电路的输出电压的目的。

2、为实现上述目的，本发明通过以下技术方案实现：

3、一种基于储能系统的buck电路自适应动态面控制方法，通过引入性能函数、误差转换函数实现给定的性能指标，并将有限覆盖引理的神经网络系统相结合，补偿传感器测量过程中产生的时间延迟；通过调整控制器参数，跟踪误差可以收敛到任意小的残集内，实现稳定buck电路的输出电压；

4、动态面控制方法基于以下步骤实现：

5、s1、采用数学变换，将一类buck类dc/dc转换器的状态空间方程变换为一般形式的数学模型，作为动态面控制方法的被控对象；

6、s2、采用性能函数和误差转换函数保证给定的跟踪性能指标；

7、s3、采用神经网络和有限覆盖引理相结合的方式近似被控对象的数学模型中具有时间延迟的未知函数；

8、s4、设计动态面控制器，将虚拟控制律通过一阶低通滤波器，使神经网络的输入已知，采用神经网络结合有限覆盖引理的技术补偿时间延迟，结合步骤s2中的性能函数和误差转换函数保证给定的跟踪性能指标，设计出配备时间延迟补偿的buck电路的自适应动态面控制器。

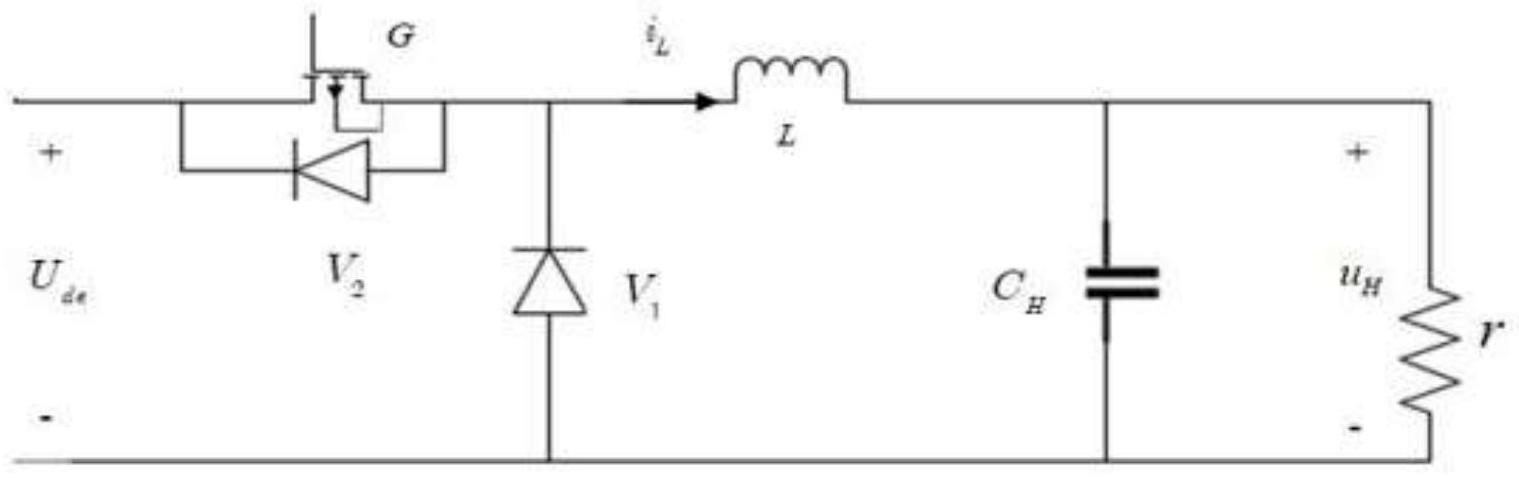
9、步骤s1一类buck类dc/dc转换器的状态空间方程如式(1)所示：

10、

11、式(1)中，uh表示电池侧电压，单位v；il表示电感电流,单位a；ude表示直流微电网直流母线电压，单位v；l为电池储能电感，单位mh；ch为电池侧滤波电容,单位mf；r为电池内阻,单位ω；不失一般性，考虑外部扰动，buck电路的状态空间方程可以采用数学变换的方式改写为如式(2)所示的数学模型，作为动态面控制方法的被控对象：

12、

13、式(2)中，需要强调的是，在控制器设计过程中，其值是未知的；τi，和di，i＝1,2，分别表示传感器测量过程中产生的未知时间延迟常数、具有时间延迟的且与电池侧电压uh相关的未知非线性函数光滑和系统的外部扰动；

14、式(2)中，u为mos管的占空比，即系统的控制输入信号；表示系统的输出；

15、对于动态面控制方法的被控对象的数学模型，规定如下假设：

16、假设1：gi≠0，i＝1,2，为未知的正常数，且满足gi≥gimin：

17、假设2：期望跟踪yr是光滑且有界的函数；属于一个紧集：

18、假设3：τi，i＝1,2，为未知的正常数，且满足0≤τi≤τm,其中，τm表示τi的最大值：

19、假设4：未知外部扰动di，i＝1,2，满足

20、为引入步骤s2采用性能函数和误差转换函数，定义跟踪误差e为，如式(3)所示：

21、e＝x1-yr (3)

22、对于t≥0的任一时刻，性能函数p(t)为一个光滑且递减的正函数，其具体形式为，如式(4)所示：

23、

24、式(4)中，0＜σ＜1和limt→∞＝p∞＞0，p∞为系统稳定时所允许的跟踪误差的最大值；为了将式(4)转化为一等价函数，引入如下形式的误差转换函数，如式(5)所示：

25、e(t):＝p(t)φ(s1), (5)

26、式(5)中，s1是由误差转换函数进行转换后的转化误差，φ(s1)是某一光滑且严格单调递增的函数，其反函数具有如下性质：

27、

28、且

29、

30、由式(7)可知，如果那么式(6)成立；再考虑p(t)＞0和式(5)，可得-σp(t)＜p(t)φ(s1)＝p(t)＜1(当e(0)＞0)或-p(t)＜p(t)φ(s1)＝p(t)＜σp(t)(当e(0)＜0)，即式(4)成立；因此，从以上分析可知，若欲实现给定的性能指标，只需证明即可；由φ(s1)的严格单调递增的性质，可得转换误差s1为：

31、

32、采用步骤s3神经网络在线逼近被控对象的数学模型中的未知的光滑函数fi:其中，表示紧集，q为输入向量的维数；神经网络近似未知函数的表达式，如式(9)所示：

33、fi(ζi)＝wi*tψi(ζi)+εi, (9)

34、式(9)中，是神经网络的输入向量；是最优权值向量，且n是神经元的节点数，如式(10)所示：

35、

36、式(10)中，是权值向量函数；κj(ζii)是径向基函数，如式(11)所示：

37、κj(ζi)＝exp[-||ζi-ξj||/2μj2],j＝1,...,n (11)

38、式(11)中：ξj是第j个基函数的中心，μj是基函数的宽度；εi是神经网络的估计误差；

39、假设5：|εi|≤υi，其中，υi表示估计误差的上界值；

40、注释1：应当强调的是，当未知光滑函数具有未知的时间延迟常数τi时，例如fi(ζi,ζi(t-τi))，不能利用神经网络直接近似；然而，由于紧集的存在，可以利用结合有限覆盖引理的神经网络对未知函数进行近似；

41、引理1：假设输入向量ζi＝(ζi,ζi(t-τi))关于时间t一致连续，其中，τi∈[0,τm]是未知时间延迟常数；继而，对于任意的给定误差存在一个独立于时间t的有限区间[0,τm]，其形式,如式(12)所示：

42、0＜t1＜…＜tm＜τm (12)

43、由式(12)中一个时间点，满足：

44、

45、可得：

46、

47、结合式引理1和假设3，存在多个时间点τ1/1,…,τn/n∈{t1,...,tm}，将具有时间延迟的未知光滑函数表示为，如式(15)所示：

48、

49、式(15)中：表示有限覆盖引理的估计误差，结合神经网络近似未知函数的表达式，式(15)可以被近似为式(16)所示：

50、

51、式中，δi表示神经网络估计误差的上界值与有限覆盖引理的估计误差之和；

52、且输入向量

53、θi＝(x1,...,xi,...,x1(t-t1),...,xk(t-τk/k),...,xi(t-tm)) (17)

54、步骤s4设计自适应动态面控制器，包括以下步骤：

55、s41、结合被控对象的数学模型，转换误差s1关于时间t的一阶导数，如式(18)所示：

56、

57、式(18)中：x2d是虚拟控制律；

58、由式(18)中可得，如式(19)所示：

59、

60、式(19)中，

61、结合式(16)，式(19)中的未知项可以写为，如式(20)所示：

62、

63、且输入向量θ1＝(x1,x1(t-t1),...,x1(t-τk/k),...,x1(t-tm),ψ)；

64、借助杨氏不等式，下式成立：

65、

66、

67、构建第一个候选李雅普诺夫函数，如式(23)所示：

68、

69、式(23)中，和是设计的正参数，估计误差和其中，和分别表示θ1和v1*的估计值；

70、结合式(19)-式(22)所获得的相关计算推导，对第一个候选李雅普诺夫函数求导可得：

71、

72、设计虚拟控制量和自适应律为：

73、

74、

75、

76、其中，k1，和均为设计的正参数；

77、将所设计的虚拟控制量和自适应律代入第一个候选李雅普诺夫函数的导数，可得如式(28)所示：

78、

79、引入如式(29)所示的一阶低通滤波器用来计算虚拟控制量的导数：

80、

81、式(29)中，τ和z1分别是时间常数和滤波器的输出；

82、将滤波误差y1定义为，如式(30)所示：

83、y1＝z1-x2d (30)

84、动态面误差s2定义为，如式(31)所示：

85、s2＝x2-z1 (31)

86、由滤波误差y1和动态面误差s2，可得如式(32)所示：

87、x2-x2d＝s2+z1-x2d＝s2+y1 (32)

88、考虑到下面的不等式：

89、

90、

91、

92、

93、

94、并结合式(32)，可以证明，如式(38)所示：

95、

96、s42、根据被控对象的数学模型，动态面误差s2的导数，如式(39)所示：

97、

98、式(39)中：，由式(39)可得，如式(40)所示：

99、

100、式(40)中，

101、构建第二个候选李雅普诺夫函数，如式(41)所示：

102、

103、式(41)中，和是设计的正参数，估计误差和其中和分别是θ2和v2*的估计值；

104、结合式(40)，对第二个候选李雅普诺夫函数求导可得，如式(42)所示：

105、

106、结合式(16)，式(42)中的未知项可以写为，如式(43)所示：：

107、

108、且输入向量θ2如式(17)所定义的相同；

109、同步骤s41，利用形如式(21)-(22)的不等式，第二个候选李雅普诺夫函数的导数可以改写为,如式(44)所示：

110、

111、设计控制律和更新律为：

112、

113、

114、

115、其中，k2，和是设计的正参数；

116、将所设计的控制律和更新律带入到第二个候选李雅普诺夫函数的导数，可得如式(48)所示：

117、

118、同步骤s41，根据杨氏不等式，式(48)可写为：

119、

120、与现有技术相比，本发明的有益效果是：

121、1.与已有的利用反步方法设计的buck电路控制器相比，动态面控制方法引入一阶低通滤波器计算虚拟控制律的导数，避免产生微分爆炸现象；并引入性能函数和误差转换函数，实现给定的性能指标；

122、2.将神经网络系统与有限覆盖引理相结合，不仅可以近似未知的光滑函数，还可以补偿系统产生的时间延迟，从而降低跟踪误差；

123、3.使用动态面控制方法所设计的控制律u(t)，可以避免由反步方法产生的微分爆炸现象，稳定性分析表明，所设计的自适应控制器能确保控制系统中的所有的更新律、设计参数等，均半全局一致终有界，借助初始化技巧，系统的跟踪误差能够收敛到一个可调的紧集。