有限转角力矩电机的转角位置控制方法与流程

1.本发明涉及电机控制领域，尤其涉及一种有限转角力矩电机的转角位置控制方法。


背景技术：

2.有限转角力矩电机(limited angle torque motor, latm)作为一种机电旋转执行器，具有通常小于
ꢀ±
180
°ꢀ
的有限角运动，已广泛应用于精密伺服系统，如光学扫描系统、航空航天系统和简单的切换阀。与传统的旋转电机相比，latm具有更高的扭矩/功率比、更低的成本、更高的可靠性和更少的机械连接部件等诸多优势。由有限转角力矩电机组成的伺服阀通过一个内置在电机轴上的偏心机构来直接驱动阀芯，该伺服阀结构简单、紧凑、体积小、重量轻、静动态性能好，具有良好的市场前景。转矩系数是评价有限转角力矩电机输出特性的重要指标，转矩系数等于单位电流输入下的力矩输出大小，转矩系数越大，电机的动态性能也越好。
3.现有的有限转角力矩电机的控制系统的普遍设计方法是，将控制对象视为一个近似的线性模型，并根据该模型设计简单的闭环位置控制系统。在控制器结构上，通常采用位置传感器构成的单闭环位置控制；在控制器硬件上，通常采用微处理器生成驱动控制信号，经功率放大电路放大后直接驱动电机；在控制器的控制算法上，通常采用pid的闭环控制算法。
4.现有的有限转角力矩电机的控制系统设计不足之处如下：1）控制对象模型建立具有较大偏差。现有的设计方法认为：有限转角力矩电机的转矩系数为定值，即在所有工作条件下，输入电流与输出转矩的呈严格线性关系。然而实际上，有限转角电机的电机模型存在较多非线性因素，如电枢电感与磁链，其转矩非线性偏差随电流与转子位置的变化而变化。这些非线性因素将导致转矩系数随着输入电流和转子转角的变化而发生变化。若输出非线性偏差较大，将会引发较为严重的转矩波动问题。即电机是一个主要受到转子角度和输入电流影响的非线性模型，这种模型建立的偏差将直接影响控制系统的性能。在高精度、快速性的应用场合中，将非线性模型视为线性模型所产生的模型偏差将会极大的制约控制系统的控制精度和响应的提高。
5.2）采用的pid控制算法与控制对象不匹配。pid控制算法是一种基于数据驱动的，不需要被控对象的精确模型就能设计的控制算法。pid控制算法对二阶以内的线性系统具有良好的控制效果。然而，在有限转角力矩电机的驱动控制中，由处理器端的电压输入到电机的转角位置的输出实际上是一个三阶受控对象，pid的控制不能实现较高的控制精度。与此同时，由于有限转角力矩电机的非线性特性的存在，被控对象实际上是一个非线性系统，当被控对象的非线性特性较明显时，采用pid控制算法的控制系统很难达到良好的控制效果。
6.3）被控对象的负载波动问题。在实际的应用过程中，电机上的负载力不是一个恒定不变的力，该力的大小会随着时间的变化而变化。于此同时，应用工况上的振动、摩擦力
等的干扰力存在，同样会影响负载力大小的波动。在负载力波动量较大的应用工况中，电机控制不能及时响应负载的变化，会导致控制响应时间的滞后。这些问题会导致控制系统的响应速度受到负载力制约，不能达到较高的动态性能。


技术实现要素：

7.为解决以上问题，本发明提供一种动态性能好、精度高、稳定性强的有限转角力矩电机的转角位置控制方法。
8.本发明采用的技术方案是：一种有限转角力矩电机的转角位置控制方法，其特征在于：包括以下步骤：s1：被控对象的建模与分析有限转角力矩电机的电机模型可以分为电磁力模型和动力学模型，在电机驱动的控制分析中，主要分析的是其动力学模型。电机的动力学模型可以由系统的运动方程组表达，而运动方程主要由电机的压电平衡方程、电磁力方程和力平衡方程得出；有限转角力矩电机的数学表达式如下： 1-1式中， 为电机的端口电压， 为电机的输入电流， 为电机绕线电阻， 为电机绕线电感， 为电机的磁通量 1-2式中， 为电机的转矩系数，由于电机的非线性特性，该系数会随着 的变化而发生变化； 1-3式中， 为转子和转子上负载的转动惯量， 为电机转子转角， 为时间， 为摩擦系数， 为应用系统中回位弹簧的刚度， 为电机输出的电磁转矩， 为负载转矩；式1-1、1-2、1-3分别为有限转角力矩电机的电气模型、电磁力模型和力学模型的数学表达式，在有限转角力矩电机的位置控制系统中，需要通过电机控制器对电机两端电压 的动态输入控制，实现被控电机转子转角 的精确控制；转子转角的输出值的精确度影响着位置控制系统的精度；电机转子的加速度决定控制系统的响应速度，加速度 的计算公式：
ꢀꢀꢀ
1-4其中， 为电机转子的角速度， 为电机转子的加速度，在有限转角力矩电机的位置控制系统中，若要保证位置控制的位置响应的快速性和稳定性，则 需要保证在一定的数值范围内；当 的值小时会造成响应时间的滞后，当 的值大时会造成位置响应的稳定性变差；s2：基于数据驱动的模型参数获取：根据有限转角力矩电机的动力学模型数学表达式可知：要获得准确的数学模型，
电机的参数：电机绕线电阻 、电机绕线电感 、转子和转子上负载的转动惯量 、摩擦系数、应用系统中回位弹簧的刚度和电机的转矩系数 ，都需要得到较为准确的测量；其中，除了 参数外，其他参数都能够通过现有的仪器进行简单的测量，并且能够获得较高的测量精度；电机的转矩系数 参数受到多种电机设计参数影响，当加工工艺的精度不能保证时，其值的波动量不能得到有效控制；针对无法直接获得的参数，可以通过搭建电机的测试实验平台，通过测试获得电机的输入输出数据，根据该数据的分析和处理，描述电机的参数特性。利用基于数据驱动方法：设计能够获得被控对象模型参数的设备，通过一定的测试方法获得大量的电机工况数据和电机实际输出数据，通过数据处理手段获得电机的转矩系数 的数学表达形式；针对该测试平台，其通过控制电机的 输入量改变电机的工况，测量在不同的输入量下的转矩 的输出值，并记录以上的输入和输出数据，采用特定的数据处理方法描绘出的关系曲线，即可得到 的数学函数表达式；s3：基于模型驱动的模型分析通过以上方法，数学表达式中的电机参数都能够得到精度较高的测量；因此可以用以上的数学模型参数描述出较为准确的电机模型；为了根据运动方程指导控制器的设计，需要对该方程做拉斯变换处理，1-1和1-2经过拉斯变换处理后得到： 3-1
ꢀꢀ
3-2根据3-1，3-2联合可以得到，当电机的端口电压作为输入量，电机的转角位置作为输出量时，系统的传递函数如下：
ꢀꢀꢀ
3-3由以上传递模型的分析可知：当忽略负载力 的变化时，该数学模型为三阶系统；传统的控制器采用的是pid控制算法，而pid控制算法更适用于二阶线性控制系统。若采用pid控制算法直接进行控制，被控对象的阶数较高，控制精度无法得到保障。同时，由于该系统存在 这一项非线性函数，pid的控制效果受到限制，控制精度会进一步下降。
9.当控制系统存在实时变化的负载力 时，转子的加速度 为：
ꢀꢀ
3-4由于负载力 会发生波动，且输出电磁力由于转矩系数的非线性特性难以实现稳定控制，因此 项的值不稳定，加速度难以得到有效的控制。当加速度的值的波动较大超出可控范围时，可能会造成系统的响应速度不足或位置响应稳定性不足。
10.作为优选，针对控制系统阶数较高，控制器采用pid控制算法会导致位置控制精度下降的问题。本发明通过引入新的闭环反馈，在控制系统中的位置闭环内的某个环节中加
入反馈量。通过该环节的闭环控制，将系统中某些带有复杂阶数的环节经过闭环反馈后变为线性环节，从而达到系统降阶的效果；其中电流反馈是一种低成本，精度较高的反馈方式，本文采用的是引入电流反馈将该三阶控制系统降低为二阶控制系统，这时pid控制就能达到较高的精度；通过引入电流闭环，使得原先对电机的驱动控制由电压控制变为电流控制。此时式3-1的压电方程被约去，控制量为电机的电流，其表达式为：
ꢀꢀꢀꢀꢀ
4-1此时，被控对象的模型由三阶模型变为了二阶模型，此时采用pid作为位置控制器的控制算法能够达到较高的控制精度，且不会要求控制器采用阶数过高过于复杂的控制算法；具体的实施方案为：在传统有限转角力矩电机的位置驱动控制器的基础上，在功率模块输出的电机控制信号部分加入电流传感器，从而检测并控制由功率模块输出的驱动电机的电流信号大小。
11.作为优选，针对该电机控制系统由于非线性系数和负载波动造成的响应速度不足或稳定性降低的问题。由于负载波动量不可预知，且控制系统存在较大非线性特性，本发明采用拓展卡尔曼(ekf)观测器来预测位置控制中加速度的变化趋势，从而提高系统的动态特性；该控制系统主要由被控电机、位置传感器、电流传感器和控制器组成，电流传感器和位置传感器构成双闭环的控制器结构；位置控制器采用pid的控制算法，在控制系统的位置控制中起到主要作用；电流控制器采用pi算法，主要起到对控制对象进行降阶(三阶降至二阶)和向ekf观测器提供有效信息的作用。ekf观测器通过获得电流传感器和位置传感器的电机转子位置和电机电流信息，通过上一时刻的系统状态估计下一时刻的系统加速度值，并将该值作为前馈参数 补偿至系统输出中，达到提高系统动态特性的效果。
12.本发明取得的有益效果是：通过数学分析的方法得到被控对象（有限转角力矩电机）的数学表达式，并根据该表达式确定需要获得的电机参数；表达式中不能直接获得的参数，通过实验测量得出的输出求出该参数的数学表达式；对所得到的具体被控对象的数学模型进行分析：对被控对象中的非线性部分做插补处理并作为软件补偿参数传输至控制器中；对被控对象中的高阶部分通过新增闭环的方法，实现控制系统的降阶处理；针对被控对象负载的波动问题，通过设计ekf观测器，预测控制对象下一时刻的加速度和速度情况，改善控制系统的动态特性。
13.本发明通过数据驱动的方法来获得被控对象的较为精确的控制模型，根据所建立的控制对象的模型，采用模型驱动的方法设计相应的电机控制器。根据以上方法设计的控制系统实现了较高精度的模型建立，并具备与之匹配的控制器结构及算法，能够达到更高的控制精度和响应速度。针对负载转矩波动的问题，本文采用拓展卡尔曼ekf观测器来预测下一时刻的转矩变化，使得控制器能够提前进行调节，以此来提高控制系统的响应速度。
附图说明
14.图1为本发明的原理图；
图2为有限转角力矩电机的数学模型框图；图3为基于数据驱动获得被控对象模型参数的设备示意图；图4为有限转角力矩电机控制器的具体电路框图；图5为有限转角力矩电机控制器的控制结构框图。
具体实施方式
15.下面将结合附图对本发明的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
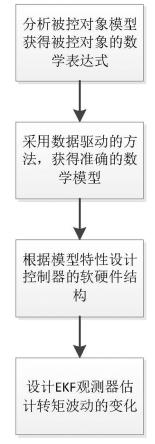
16.如图1所示，本发明的一种有限转角力矩电机的转角位置控制方法，采用了基于数据驱动的模型获取方法和基于模型的控制器设计方法，包括：对控制对象的数学模型建立、采用数据驱动的方式测量控制对象数学模型参数值、对控制对象的数学模型进行模型分析和提出改进的控制器硬件和软件结构。
17.控制对象的动力学数学模型建立，主要包括电机动力学模型中的压电平衡方程、电磁方程和力平衡方程。得到三个方程的数学表达式后，即可联合建立电机的运动方程。
18.数据驱动的方式测量控制对象数学模型参数值，其原理是通过不断改变电机的工作状态，测量不同工作状态下的电机输出，从而获得大量的电机状态-电机输出的对应关系数据，进而拟合出电机某项参数特性。在本发明中具体的指通过不断地改变电机的工作转角和驱动电流，并实时测量电机的转矩输出，得到电机电流-电机转子转角-电机转矩输出的大量数据，最后通过该数据得到电机的非线性转矩系数 的表达式。
19.控制对象数学模型分析，主要是通过对控制对象的运动方程进行拉斯变换，联合得到控制系统输入输出的拉斯变换表达式，通过该表达式可以分析出系统的阶数和需要采用的控制算法。本发明的位置控制算法采用的是pid算法，而控制对象的阶数为三阶，pid算法不能适配，因此通过引入新的电流闭环将控制对象的输入量变为电流，从而将控制对象变为二阶模型，使得pid算法达到更好的控制效果。
20.改进控制器的硬件和软件结构设计，硬件结构设计主要是指对控制系统的硬件结构进行改进，包括新增的电流闭环的结构和具体实施方案。软件设计主要是指对控制器的软件结构进行设计，包括位置控制器的设计、电流控制器的设计、ekf观测器的设计，控制器各个结构之间的关系以及信号传输。
21.本发明的有限转角力矩电机的转角位置控制方法，具体包括以下步骤：s1：被控对象的建模与分析有限转角力矩电机的电机模型可以分为电磁力模型和动力学模型，在电机驱动的控制分析中，主要分析的是其动力学模型。电机的动力学模型可以由系统的运动方程组表达，而运动方程主要由电机的压电平衡方程、电磁力方程和力平衡方程得出；有限转角力矩电机的数学表达式如下：
ꢀꢀꢀ
1-1式中， 为电机的端口电压， 为电机的输入电流， 为电机绕线电阻， 为电机绕线电感， 为电机的磁通量；
ꢀꢀꢀ
1-2式中， 为电机的转矩系数，由于电机的非线性特性，该系数会随着 的变化而发生变化；
ꢀꢀꢀ
1-3式中， 为转子和转子上负载的转动惯量， 为电机转子转角， 为时间， 为摩擦系数， 为应用系统中回位弹簧的刚度， 为电机输出的电磁转矩， 为负载转矩；如图2所示，式1-1、1-2、1-3分别为有限转角力矩电机的电气模型、电磁力模型和力学模型的数学表达式，在有限转角力矩电机的位置控制系统中，需要通过电机控制器对电机两端电压 的动态输入控制，实现被控电机转子转角 的精确控制；转子转角 的输出值的精确度影响着位置控制系统的精度；电机转子的加速度 决定控制系统的响应速度，加速度的计算公式：
ꢀꢀꢀ
1-4其中， 为电机转子的角速度， 为电机转子的加速度，在有限转角力矩电机的位置控制系统中，若要保证位置控制的位置响应的快速性和稳定性，则 需要保证在一定的数值范围内；当 的值小时会造成响应时间的滞后，当的值大时会造成位置响应的稳定性变差；s2：基于数据驱动的模型参数获取：根据有限转角力矩电机的动力学模型数学表达式可知：要获得准确的数学模型，电机的参数：电机绕线电阻 、电机绕线电感 、转子和转子上负载的转动惯量 、摩擦系数 、应用系统中回位弹簧的刚度和电机的转矩系数 ，都需要得到较为准确的测量；其中，除了参数外，其他参数都能够通过现有的仪器进行简单的测量，并且能够获得较高的测量精度；电机的转矩系数 参数受到多种电机设计参数影响，当加工工艺的精度不能保证时，其值的波动量不能得到有效控制；针对无法直接获得的参数，可以通过搭建电机的测试实验平台，通过测试获得电机的输入输出数据，根据该数据的分析和处理，描述电机的参数特性。图3是一种基于数据驱动方法获得被控对象模型参数的设备，该设备通过大量的电机工况数据和电机实际输出数据，通过一定的测试方法和数据处理手段获得了电机的转矩系数 的数学表达形式；针对该测试平台，其通过控制电机的 输入量改变电机的工况，测量在不同的输入量下的转矩 的输出值，并通过记录以上的输入和输出数据，采用特定的数据处理方法描绘出 的关系曲线，即可得到 的数学函数表达式；s3：基于模型驱动的模型分析通过以上方法建立的数学表达式中的电机参数值都能够得到精度较高的测量，因此可以用以上的数学模型描述出较为准确的电机模型。为了根据运动方程指导控制器的设计，需要对该方程做拉斯变换处理，1-1和1-2经过拉斯变换处理后得到：
ꢀꢀꢀꢀꢀꢀ
3-1
ꢀꢀꢀꢀ
3-2根据3-1，3-2联合可以得到，当电机的端口电压作为输入量，电机的转角位置作为输出量时，系统的传递函数如下：
ꢀꢀꢀ
3-3由以上传递模型的分析可知：当忽略负载力 的变化时，该数学模型为三阶系统；传统的控制器采用的是pid控制算法，而pid控制算法更适用于二阶线性控制系统。若采用pid控制算法直接进行控制，被控对象的阶数较高，控制精度无法得到保障。同时，由于该系统存在这一项非线性函数，pid的控制效果受到限制，控制精度会进一步下降。
22.当控制系统存在实时变化的负载力 时，转子的加速度 为：
ꢀꢀꢀ
3-4由于负载力 会发生波动，且输出电磁力 由于转矩系数的非线性特性难以实现稳定控制，以此 项的值不稳定，加速度难以得到有效的控制。当加速度的值的波动较大超出可控范围时，可能会造成系统的响应速度不足或位置响应稳定性不足。
23.根据以上对控制系统的模型分析，得到了原控制系统精度和响应速度受限的原因。针对该原因，对原有的控制器的改进方案为：1、针对系统阶数过高问题的控制器硬件设计：结合图4所示，针对控制系统阶数较高，控制器采用pid控制算法会导致位置控制精度下降的问题。本发明通过引入新的闭环反馈，在控制系统中的位置闭环内的某个环节中加入反馈量。通过该环节的闭环控制，将系统中某些带有复杂阶数的环节经过闭环反馈后变为线性环节，从而达到系统降阶的效果；其中电流反馈是一种低成本，精度较高的反馈方式，本文采用的是引入电流反馈将该三阶控制系统降低为二阶控制系统，这时pid控制就能达到较高的精度；通过引入电流闭环，使得原先对电机的驱动控制由电压控制变为电流控制。此时式3-1的压电方程被约去，控制量为电机的电流，其表达式为：
ꢀꢀꢀ
4-1此时，被控对象的模型由三阶模型变为了二阶模型，此时采用pid作为位置控制器的控制算法能够达到较高的控制精度，且不会要求控制器采用阶数过高过于复杂的控制算法；具体的实施方案为：在传统有限转角力矩电机的位置驱动控制器的基础上，在功率模块输出的电机控制信号部分加入电流传感器，从而检测并控制由功率模块输出的驱动电机的电流信号大小；2、针对系统响应速度问题的控制器软件设计：针对该电机控制系统由于非线性系数和负载波动造成的响应速度不足或稳定性降低的问题。由于负载波动量不可预知，且控制系统存在较大非线性特性，本发明采用拓展卡尔曼(ekf)观测器来预测位置控制中加速
度的变化趋势，从而提高系统的动态特性；电机控制系统的控制结构框图如图5所示，该控制系统主要由被控电机、位置传感器、电流传感器和控制器组成，电流传感器和位置传感器构成双闭环的控制器结构；位置控制器采用pid的控制算法，在控制系统的位置控制中起到主要作用；电流控制器采用pi算法，主要起到对控制对象进行降阶(三阶降至二阶)和向ekf观测器提供有效信息的作用。ekf观测器通过获得电流传感器和位置传感器的电机转子位置和电机电流信息，通过上一时刻的系统状态估计下一时刻的系统加速度值，并将该值作为前馈参数 补偿至系统输出中，达到提高系统动态特性的效果。
24.拓展卡尔曼（ekf）观测器的计算过程分为两步，第一步是预测，第二步是数据更新。
25.1、预测：
ꢀꢀ
5-1式子中， 、 是希望预测的变量的前一时刻和当前时刻，在本文中代表的是加速度量； 是状态转移矩阵，作用是能根据变量当前状态计算出下一个状态的变量值； 是控制量矩阵，在本文中是电流 控制和位置 ； 是一个雅可比矩阵，与 相似用于状态预测，但其矩阵参数值不变；已知被控对象的实际模型，可以根据模型公式推测出模型的下一个状态，比如在式3-2和3-4中：
ꢀꢀ
3-2
ꢀꢀ
3-4假设，在负载力矩不变的情况下，式3-4中可以通过测量电机输出力矩 的值直接计算出加速度 ，而，也就是根据电流和位置信息，可以直接求出 。
26.但当系统有不确定量 且不断变化时，预测就会出现偏差。系统的不确定量 和控制量存在一定的关系，这个关系用协方差 表示。关系的相关程度越大，直接作用在该变量上的作用程度越大。
27.式3-2变形可以得到某一时刻的负载转矩和电流角度有某种数学关系，但是这种关系是不稳定；因为负载 的下一时刻变化量是不确定的，下一时刻的、 的值很难计算并和它匹配，因此不同时刻的、 与的协方差 并不相同；式5-2为当前时刻的协方差更新公式，通过上一时刻的 、 数据来更新这个不断变化的协方差；
ꢀꢀ
5-2其中 是协方差矩阵， 是上文的状态转移矩阵， 是传感器测量误差矩
阵；通过上一时刻的数据得到当前时刻的理想观测量 ，同时更新当前时刻协方差矩阵 。
28.2、预测数据更新：计算出理想情况下的 值后，由于没有补偿下一时刻的负载转矩变化，因此预测值和现实一定存在差值，这个差值用卡尔曼系数 补偿：
ꢀꢀꢀ
5-3得到了一个负载变化的补偿系数；
ꢀꢀ
5-4式5-4将补偿系数通过计算，补偿到原来理想情况下的 值中，达到了无限接近下一时刻的观测量加速度 的效果；所达到的效果是：负载力无论怎么变化，由于力的变化不会在时间上剧烈突变，通过上一时刻的力波动趋势就可以预测并补偿下一时刻的加速度输出，达到输出稳定的加速度的效果。
29.ꢀꢀ
5-5式5-5，同样更新入协方差中，供下一时刻使用。
30.到此卡尔曼一轮计算完毕，通过拓展卡尔曼滤波，首先计算出了理想情况的加速度是多少，确定下一时刻的加速度输出的基础值。下一时刻的负载相比于上一时刻会变化，该变化与 、 的变化趋势有关系，因此通过更新协方差矩阵，得到卡尔曼补偿系数，将负载力的变化情况补偿入加速度的输出中。最终实现了加速度的稳定控制，使得其不会太高也不会太低，保证了系统的响应速度和稳定性。
31.本发明的有限转角力矩电机的转角位置控制方法，采用了高性能位置控制器，该控制器包括电流控制器、位置控制器和ekf观测器。
32.位置控制器采用pid算法，根据目标位置信号 和位置反馈值进行运算，得到传输给下一级的加速度控制信号 。
33.电流控制器采用pi算法，根据目标加速度信号换算来的电流信号 和电流反馈值 ，控制电机的输入电流。
34.加速度控制信号 和输入电流 信号的表达式为：信号的表达式为：其中 ， ， 分别表示pid中的比例项、积分项、微分项， 和 的取值范围都为[-1,1]。
[0035]
ekf观测器用于根据采集到的当前时刻的电流信号和位置信号的偏差值 估计此刻的输出转矩波动和负载转矩波动情况，并对下一时刻的加速度信号进
行预测推理。ekf观测器经过运算后得到加速度控制信号 的前馈修正值并对该信号进行前馈修正，得到下一时刻的加速度修正信号。加速度修正信号 在经过换算后，得到电机电流控制信号，该信号能够更好的应对输出转矩和负载转矩的变化对加速度控制的影响。该ekf观测器能够实现位置控制器的对加速度有效控制，从而提高系统的响应速度和稳定性。
[0036]
用于描述本说明书和权利要求的各方面公开的形状、尺寸、比率、角度和数字仅仅是示例，因此，本说明书和权利要求的不限于所示出的细节。在以下描述中，当相关的已知功能或配置的详细描述被确定为不必要地模糊本说明书和权利要求的重点时，将省略详细描述。
[0037]
在使用本说明书中描述的“包括”、“具有”和“包含”的情况下，除非使用 否则还可以具有另一部分或其他部分，所用的术语通常可以是单数但也可以表示复数形式。
[0038]
应该指出，尽管在本说明书可能出现并使用术语“第一”、“第二”、“顶部”、“底部”、“一侧”、“另一侧”、“一端”、“另一端”等来描述各种不同的组件，但是这些成分和部分不应受这些术语的限制。这些术语仅用于区分一个成分和部分和另一个成分和部分。例如，在不脱离本说明书的范围的情况下，第一部件可以被称为第二部件，并且类似地，第二部件可以被称为第一部件，顶部和底部的部件在一定情况下，也可以彼此对调或转换；一端和另一端的部件可以彼此性能相同或者不同。
[0039]
在描述位置关系时，例如，当位置顺序被描述为“在...上”、“在...上方”、“在...下方”和“下一个”时，除非使用“恰好”或“直接”这样的词汇或术语，此外则可以包括它们之间不接触或者接触的情形。如果提到第一元件位于第二元件“上”，则并不意味着在图中第一元件必须位于第二元件的上方。所述部件的上部和下部会根据观察的角度和定向的改变而改变。因此，在附图中或在实际构造中，如果涉及了第一元件位于第二元件“上”的情况可以包括第一元件位于第二元件“下方”的情况以及第一元件位于第二元件“上方”的情况。在描述时间关系时，除非使用“恰好”或“直接”，否则在描述“之后”、“后续”、“随后”和“之前”时，可以包括步骤之间并不连续的情况。本发明的各种实施方案的特征可以部分地或全部地彼此组合或者拼接，并且可以如本领域技术人员可以充分理解的以各种不同地构造来执行。本发明的实施方案可以彼此独立地执行，或者可以以相互依赖的关系一起执行。
[0040]
最后，应当指出，以上实施例仅是本发明较有代表性的例子。显然，本发明不限于上述实施例，还可以有许多变形。凡是依据本发明的技术实质对以上实施例所做的任何简单修改、等同变化及修饰，均应认为属于本发明的保护范围。