一种延时系统中的PID控制器参数整定方法

本发明涉及扰动估计及抑制领域，具体涉及一种延时系统中的pid控制器参数整定方法，进一步提升系统上升时间、调节时间等动态响应性能指标以及系统的抗干扰能力。

背景技术：

1、在工程控制应用中，系统经常受到外部扰动和自身内部不确定性影响，这些扰动严重影响系统稳定性能和控制效果，甚至可能造成闭环系统不稳定。以惯性稳定系统为例，文献[3](tian j,yang w,peng z,et al.application of mems accelerometers andgyroscopes in fast steering mirror control systems[j].sensors,2016,16(4):440.)中采用光纤陀螺仪、加速度计、高分辨率位置探测器组成了多回路反馈控制系统，系统总扰动抑制能力是各回路作用的叠加，但这种方法需要在惯性稳定平台上安装额外的惯性传感器，不利于实现惯性稳定平台小惯性和快速性的要求，同时也增加了实验空间和经济成本。文献[4](glück m,pott j u,sawodny o.piezo-actuated vibrationdisturbance mirror for investigating accelerometer-based tip-tiltreconstruction in large telescopes[j].ifac-papersonline,2016,49(21):361-366.)中对于由基座传感器测量到的外部振动，采用基于测量的直接前馈方法进行抑制，但需要准确识别从基座到倾斜镜的扰动传递特性。文献[5](tang t,niu s,chen x,etal.disturbance observer-based control of tip-tilt mirror for mitigatingtelescope vibrations[j].ieee transactions on instrumentation and measurement,2018,68(8):2785-2791.)将dob引入到惯性稳定系统来增强系统抗干扰能力。然而，被控对象模型的特性往往不能被准确识别，补偿器的设计受到限制。

2、为了进一步提高系统的扰动抑制能力，一种可以用来观测外部扰动和系统内部不确定性的扩张状态观测器被广泛使用。传统的线性扩张状态观测器设计方法将外部扰动和系统内部不确定归为总扰动，并将其扩张为一个状态变量进行观测和补偿。这种设计方法下的系统将被简化为双积分串联标准型，降低了控制的难度。但是，在传统扩张状态观测器的设计中与已知模型信息没有关系，这会使观测器的观测精度的下降，导致系统抗干扰能力下降。本发明对传统的扩张状态观测器设计进行改进，使观测器的观测精度上升。

3、随着经典控制理论的不断发展，线性二次型最优控制在现代控制理论中有着广泛的应用。线性二次型最优控制方法得到的最优控制律具有许多优良的特性，包括闭环稳定性以及系统过程为单输入单输出时，线性二次型最优控制下的系统相位裕度至少为60°，系统幅值裕度为无穷大。此外，线性二次型最优控制方法中通过选择加权矩阵q和r，可以控制状态调节要求和控制能量消耗之间的权衡。这种优良的性质促使控制设计师将其用于pid控制器参数的整定。本发明中采用线性二次型最优控制与主导极点配置技术相结合的方法对带有改进后的扩张状态观测器的延时系统进行pid控制器参数进行整定。

技术实现思路

1、本发明目的在于：由于工程控制应用中系统延时因素对系统稳定性的影响不可忽略，针对延时系统中存在的建模误差以及不确定扰动问题，本发明提供了一种延时系统中的pid控制器参数整定方法。

2、本发明采用的技术方案为：一种延时系统中的pid控制器参数整定方法，具体实施步骤如下：

3、针对二阶模型系统g(s)：

4、

5、其中，a1＝2ζolωol，ζol、ωol分别为开环系统的阻尼比和固有频率；b为开环系统增益；l为系统的延时系数。

6、步骤1：建立系统微分方程：

7、

8、其中，y,u为系统输出和输入，w为外部扰动，为部分模型信息，a0,a1,b为系统已知参数；由于在实际中a0,a1,b通常辨识得不精确，采用fx表示模型不准确的部分和内部动力学变化的部分；fw表示外部扰动；表示已知模型动力学和未知扰动的综合效应。

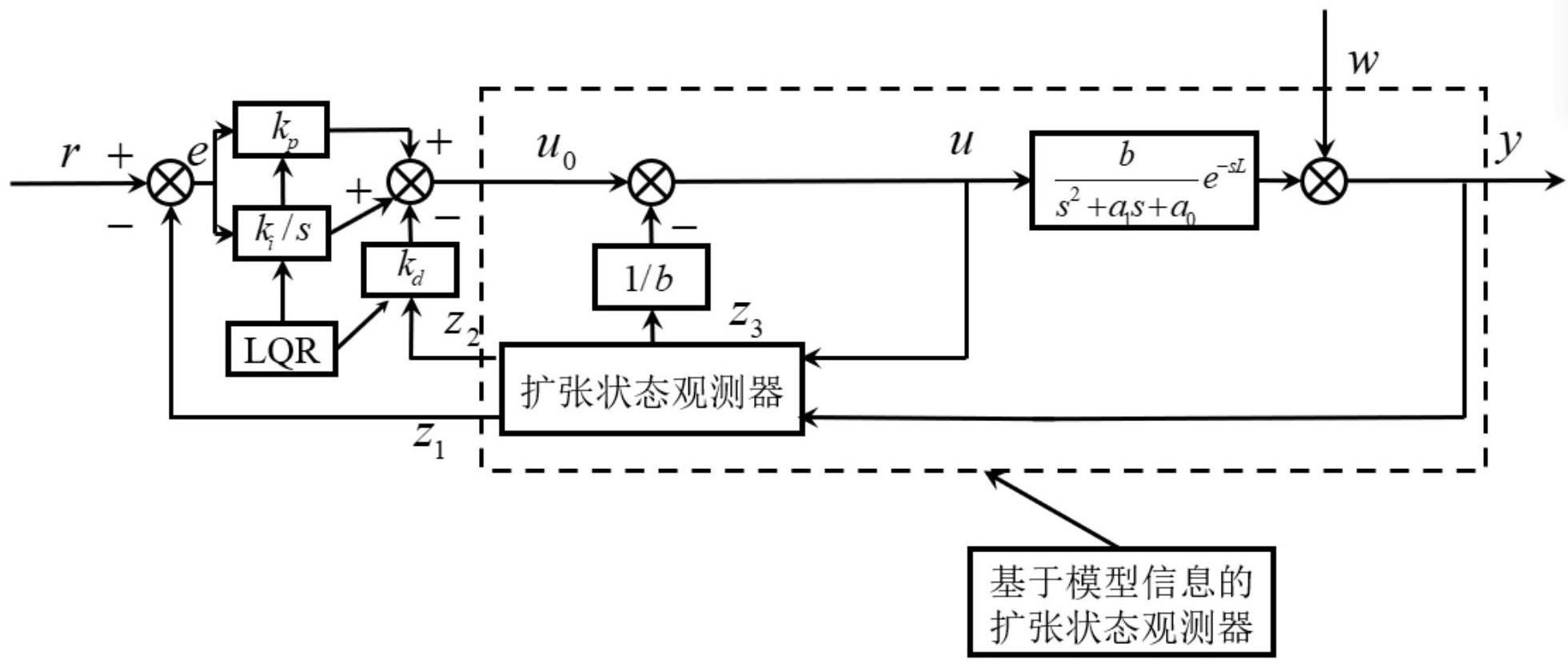
9、将微分方程转化为扩张状态空间方程形式，系统扩张状态空间方程如下：

10、

11、其中，分别表示延时系统中的位置、速度以及系统总扰动。

12、步骤2：根据线性系统理论中状态观测器的设计，连续扩展状态观测器eso如下所示：

13、

14、其中，z＝[z1 z2 z3]t为观测器状态向量，l＝[β1 β2 β3]t为需要确定的观测器增益矩阵，uc＝[u(t-l) y(t-l)]t为观测器输入组合，yc为扩张状态观测器输出。

15、步骤3：扩张状态观测器可在一定频率范围内准确估计不确定扰动f′，并对扩展状态z3进行补偿，如图1所示。图1中控制信号u(t-l)为：

16、u(t-l)＝u0(t-l)-z3/b＝u0(t-l)-(fx+fw)/b (1.49)

17、将公式(1.49)带入公式(1.46)中，可以得到：

18、

19、将可用的动力学模型带入公式(1.50)中，系统排除不必要的干扰后，系统变为：

20、

21、将公式(1.51)改写为传递函数为：

22、

23、通过与公式(1.45)比较，公式(1.51)中的系统传递函数与公式(1.45)中的模型一致。这是本发明中对线性扩张状态观测器的改进。传统的线性扩张状态观测器设计方法与已知模型信息无关，系统将被简化为双积分串联标准型。

24、步骤4：采用线性二次型最优控制(lqr)以及主导极点技术相结合的方法来整定图1控制框架中pid控制器参数，实现对扰动补偿后的系统控制。图1中u0(t)为pid控制器，如下所示：

25、u0(t)＝kpx2(t)+kix1(t)+kdx3(t) (1.53)

26、其中，kp,ki,kd分别为比例元素x2(t)、积分元素x1(t)和微分元素x3(t)前对应的系数；e(t)为跟踪误差信号。

27、在外部扰动w(t)以及系统参考信号r(t)作用下，被控对象位置输出信号为y(t)，假设参考信号r(t)＝0，则跟踪误差e(t)＝r(t)-y(t)＝-y(t)，在此条件下，被控系统公式(1.52)可以表示为：

28、

29、根据状态空间的形式，被控系统公式(1.52)中状态变量的导数可以写成：

30、

31、其中，

32、

33、a,b,x,l分别是状态转移矩阵、控制矩阵、状态矩阵和时滞项。从公式(1.55)中可以看出：当t<l时，控制信号是无效的，只有当t>＝l时，控制信号有效。因此，将公式(1.55)分成两部分：如下：

34、

35、

36、公式(1.58)中um(t)为：

37、um(t)＝u0(t-l) (1.59)

38、通过公式(1.59)中的变化，即um(t)充当一个中间变量。从数学角度来说，公式(1.57)、公式(1.58)现在是无延迟的，可以应用无延迟过程的标准lqr方法来找到最优控制向量um(t)。

39、为了使公式(1.56)系统具备lqr的性能，需要将如下的二次型代价函数最小化：

40、

41、其中，q为半正定状态权矩阵，r为正定控制权矩阵。标准lqr方法给出了最优控制向量um(t)为：

42、um(t)＝-r-1btpx(t) (1.61)

43、其中，p为对称正定riccati系数矩阵，可通过求解如下连续代数riccati方程得到：

44、atp+pa+q-pbr-1btp＝0 (1.62)

45、从公式(1.59)中得到：

46、u0(t)＝um(t+l)＝-r-1btpx(t+l) (1.63)

47、公式(1.63)给出了u0(t)在t>＝0整个时间范围内的控制信号，然而x(t+l)在时间t时的值是不知道的。根据文献[1](he j b,wang q g,lee t h.pi/pid controllertuning via lqr approach[j].chemical engineering science,2000,55(13):2429-2439.)中的结论，此时最优控制向量u0(t)为：

48、

49、

50、其中ac为：

51、ac＝a-br-1btp(1.66)

52、由于公式(1.66)中得到的系统矩阵不包含任何时间延迟，因此直接应用极点配置的方法来得到期望的闭环时间性能。将公式(1.61)带入到公式(1.58)，可以得到：

53、

54、然后通过建立闭环系统的特征方程△(s)＝|si-ac|等于所要求的闭环方程。

55、当ac为2×2矩阵时，特征方程△(s)如下所示：

56、

57、其中ζcl、ωcl为阻尼比和固有频率。

58、当ac为3×3矩阵时，利用主导极点配置方法，特征方程△(s)如下所示：

59、

60、其中非主导极点p3＝mζclωcl距离主闭环极点p1,p2的实部m倍，m的值应该选择在3或更多。

61、步骤5：在线性二次型最优控制中，标准做法是通过改变加权矩阵q和保持加权矩阵r不变来进一步设计控制器参数。

62、假设，

63、

64、通过公式(1.56)、(1.66)以及(1.70)，可以得到相应的闭环系统特性方程如下：

65、△(s)＝|si-ac|＝s3+(a1+ηp33)s2+(a0+ηp23)s+ηp13(1.71)

66、其中，η＝r-1b2。

67、通过对比公式(1.69)与公式(1.73)右边相同状态变量前的系数，可以得到：

68、

69、矩阵p和矩阵q的剩余元素可通过求解riccati方程式(1.62)得到，如下所示：

70、

71、步骤6：为了得到最优控制信号u0(t)，需要计算ea(l-t)。

72、

73、其中，p01和p02是公式(1.54)开环系统的极点，如下：

74、

75、通过使用部分分式法，f1′1,f1′2,f1′3,f2′1f2′2,f2′3,f3′1,f3′2,f3′3计算如下：

76、

77、

78、

79、步骤7：为了得到最优控制信号u0(t)，需要计算

80、

81、其中，γ＝ηp13,α＝a1+ηp33,β＝a0+ηp23。

82、的计算如下：

83、

84、通过使用部分分式法，f11,f12,f13,f21,f22,f23,f31,f32,f33计算如下：

85、

86、其中，

87、

88、p1,p2,p3与公式(1.25)中的p1,p2,p3一致。

89、步骤8：联立公式(1.79)、(1.76)以及(1.64)，计算0≤t<l的pid参数。

90、

91、对比公式(1.53)与公式(1.81)，可以得到pid控制器参数：

92、

93、步骤9：联立公式(1.79)以及(1.65)，计算t≥l的pid参数。

94、

95、对比公式(1.53)与公式(1.83)，可以得到pid控制器参数：

96、

97、其中，kp,ki,kd分别为比例元素x2(t)、积分元素x1(t)和微分元素x3(t)前对应的系数；

98、步骤10：设计扩张状态观测器增益矩阵。假设误差状态变量为e(t)＝x(t)-z(t)，由公式(1.48)减去公式(1.47)，则观测器误差矩阵方程为：

99、

100、从上式可以看出，观测器误差矩阵方程中，(a1-lc)决定了闭环系统的特征值。通过保证(a1-lc)的特征值小于零，则观测器方程收敛。观测器误差矩阵方程对应得特征方程如下所示：

101、|si-(a1-lc)|＝s3+(β1+a1)s2+(a0+a1β1+β2)s+β3 (1.86)

102、根据相关文献[2](herbst g.a simulative study on active disturbancerejection control(adrc)as a control tool for practitioners[j].electronics,2013,2(3):246-279.)结论，扩张状态观测器经过参数化，可将对应的特征方程的极点放到同一位置上(-w0,w0为观测器带宽)，如下所示：

103、|si-(a1-lc)|＝(s+ωo)3＝s3+3ωos2+3ωo2s+ωo3 (1.87)

104、将公式(1.86)与公式(1.87)右边相同变量前的系数进行比较，可以得到：

105、

106、根据以上技术方案，可以实现以下有益效果：

107、1.与未带有改进扩张状态观测器的方法进行相比，本发明设计方法下系统的抗干扰能力得到进一步提升，即本发明中的改进扩张状态观测器方法有效。

108、2.与其他时域优化方法(性能指标函数为平方误差积分(ise)、时间平方误差积分(itse)、绝对误差积分(iae)、时间绝对误差积分(itae))相比，本发明设计方法下系统上升时间、调节时间等动态响应性能指标以及系统抗干扰能力得到显著改善。