一种用于群体智能系统的编队协同控制方法

本发明属于群体智能系统，具体涉及一种群体智能系统的编队协同控制方法。

背景技术：

1、近年来，群体智能系统的编队控制技术得到了广泛的研究，如：多架无人机在飞行的同时保持紧凑的编队构型，可以降低空气阻力对后排无人机的干扰，进而降低能量的消耗，提升无人机集群的续航能力；多颗卫星通过维持特定的编队构型，能够最大化其感知和侦察的范围。

2、在实际中，目标编队构型通常是利用编队向量来构造的，其构造过程比较繁琐且不易实现构型变换；另外，相较于渐进收敛的编队控制，在有限的时间内形成目标编队并完成任务显然更具实际意义，也更符合实际的任务需求。因此，如何设计一种能够在任意精确的时刻实现可灵活变换构型的编队控制方法已成为亟待解决的技术问题。

技术实现思路

1、针对现有技术中的上述不足，本发明提供的一种群体智能系统的编队协同控制方法解决了群体智能系统中编队向量构造过程复杂且不易实现构型变换的问题。

2、为了达到上述发明目的，本发明采用的技术方案为：

3、一种用于群体智能系统的编队协同控制方法，包括以下步骤：

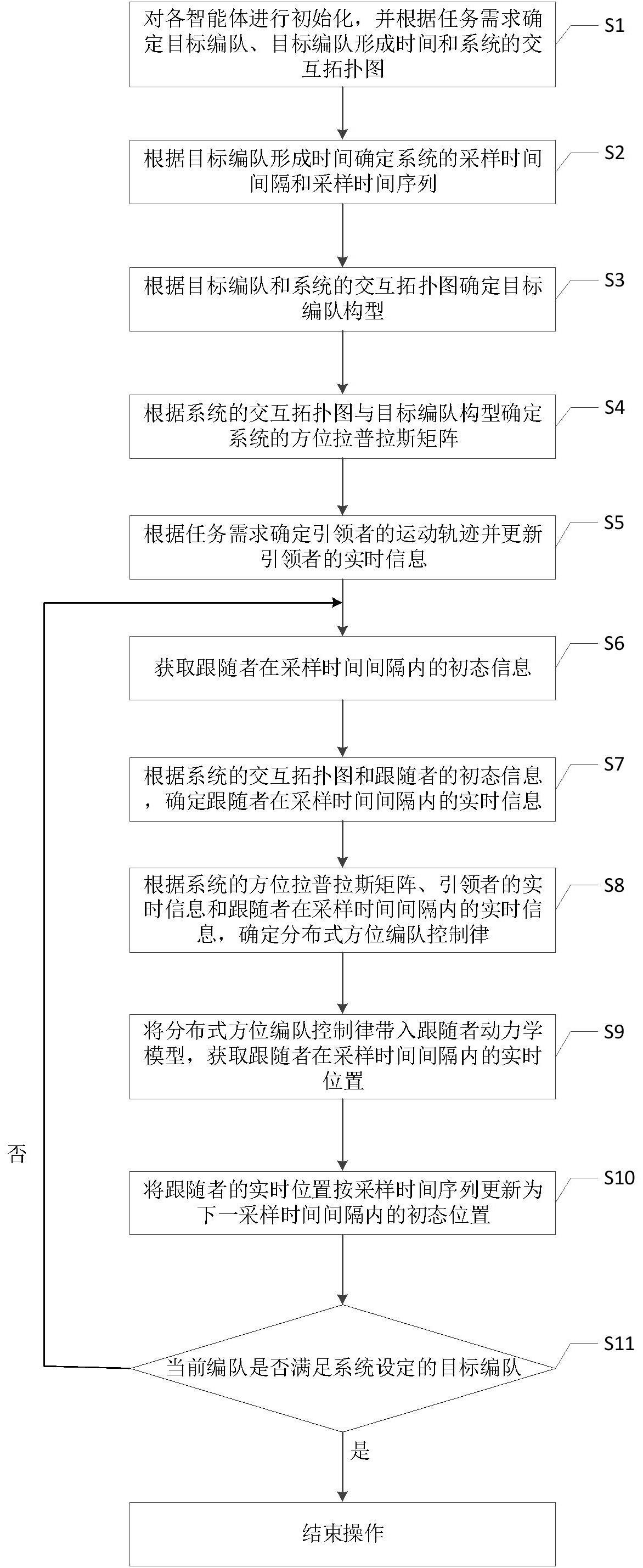
4、s1、对各智能体进行初始化，并根据任务需求确定目标编队、目标编队形成时间和系统的交互拓扑图；

5、s2、根据目标编队形成时间确定系统的采样时间间隔和采样时间序列；

6、s3、根据目标编队和系统的交互拓扑图确定目标编队构型；

7、s4、根据系统的交互拓扑图与目标编队构型确定系统的方位拉普拉斯矩阵；

8、s5、根据任务需求确定引领者的运动轨迹并更新引领者的实时信息；

9、s6、获取跟随者在采样时间间隔内的初态信息；

10、s7、根据系统的交互拓扑图和跟随者的初态信息，确定跟随者在采样时间间隔内的实时信息；

11、s8、根据系统的方位拉普拉斯矩阵、引领者的实时信息和跟随者在采样时间间隔内的实时信息，确定分布式方位编队控制律；

12、s9、将分布式方位编队控制律带入跟随者动力学模型，获取跟随者在采样时间间隔内的实时位置；

13、s10、将跟随者的实时位置按采样时间序列更新为下一采样时间间隔内的初态位置；

14、s11、判断当前编队是否满足系统设定的目标编队；若是则结束操作，否则跳转到步骤s6。

15、进一步地，步骤s2包括以下分步骤：

16、s21、根据目标编队形成时间，计算采样时间间隔，表示为：

17、

18、其中：为采样时间间隔， k为采样时间系数，为目标编队形成时间；

19、s22、根据采样时间间隔，构建系统的采样时间序列：

20、

21、其中： tm为第 m个采样时间序列。

22、进一步地，步骤s4包括以下分步骤：

23、s41、根据智能体的位置计算智能体的相对方位，表示为：

24、

25、其中：为智能体 j相对于智能体 i在目标编队中的相对方位，为智能体 j在目标编队中的位置，为智能体 i在目标编队中的位置，为2-范数；

26、s42、根据分步骤s41中智能体的相对方位，计算所述相对方位对应的正交投影矩阵，表示为：

27、

28、其中：为智能体 j相对于智能体 i在目标编队中的相对方位对应的正交投影矩阵， id为维度为 d的单位矩阵， t为矩阵的转置计算符号，为的实矩阵；

29、s43、根据分步骤s42中得到的正交投影矩阵，构造系统的方位拉普拉斯矩阵：

30、

31、其中：为系统的方位拉普拉斯矩阵，为系统交互拓扑图的边集，为智能体 i的邻居集，为智能体 k相对于智能体 i在目标编队中的相对方位对应的正交投影矩阵，为系统交互拓扑图的节点集。

32、进一步地，按照引领者-跟随者的结构，将系统的方位拉普拉斯矩阵表示为：

33、

34、其中：为引领者和引领者之间的方位矩阵，为跟随者相对于引领者的方位矩阵，为引领者相对于跟随者的方位矩阵，为跟随者和跟随者之间的方位矩阵。

35、进一步地，在步骤s5中，根据目标编队确定引领者的运动轨迹为：

36、

37、其中：为智能体 i在 t时刻的位置，为智能体 i在目标编队中的位置，为引领者的集合。

38、进一步地，在步骤s7中，选取跟随者在采样间隔的实时位置为其自身与邻居初态位置的加权平均值，表示为：

39、

40、其中：为智能体 i在第 k个采样时间间隔的实时位置， tk为第 k个采样时间间隔的初始时刻， tk+1为第 k个采样时间间隔的终端时刻，为常对角矩阵，为智能体 i的邻居集，为智能体 j相对于智能体 i在目标编队中的相对方位对应的正交投影矩阵，为智能体 j相对于智能体 i的相对方位，为智能体 j在第 k个采样时间间隔的位置， id为维度为 d的单位矩阵，为智能体 i在第 k个采样时间间隔的位置。

41、进一步地，步骤s8包括以下分步骤：

42、s81、根据最优控制中变分法，确定该采样时间间隔内的代价函数，表示为：

43、

44、其中：为在时间间隔上的代价函数， tk为第 k个采样时间间隔的初始时刻， tk+1为第 k个采样时间间隔的终端时刻，为实时控制输入， t为矩阵的转置计算符；

45、s82、根据最优控制中变分法，确定该采样时间间隔内的哈密尔顿函数，表示为：

46、

47、其中：为在时间间隔上的哈密尔顿函数， n为智能体的个数， nf为系统中跟随者的个数，为协态变量；

48、s83、求解分步骤s81中代价函数对应的正则方程和s82中哈密尔顿函数对应的正则方程，并记录求解结果；

49、s84、根据迭代算法确定常对角矩阵；

50、s85、根据分步骤s83中的求解结果和分步骤s84中确定的常对角矩阵，并结合步骤s7中跟随者在采样时间间隔内的终态信息，得到分布式方位编队控制律的解析式：

51、

52、

53、其中：为实时控制输入，为常对角矩阵， tk为第 k个采样时间间隔的初始时刻， tk+1为第 k个采样时间间隔的终端时刻，为智能体 i的邻居集，为智能体 j相对于智能体 i在目标编队中的相对方位对应的正交投影矩阵，为智能体 j相对于智能体 i的相对方位，为智能体 i在第 k个采样时间间隔的位置，为智能体 j在第 k个采样时间间隔的位置，为跟随者的集合。

54、进一步地，步骤s84包括以下分步骤：

55、s841、根据步骤s4中系统的方位拉普拉斯矩阵确定各子矩阵等式：

56、

57、其中：为第一子矩阵，为矩阵 d的第1个对角线元素，为矩阵的一阶顺序主子式，为跟随者和跟随者之间的方位矩阵，为第 d子矩阵，为括号内元素构成的对角矩阵，为矩阵 d的第 d个对角线元素，为矩阵的 d阶顺序主子式，为第 d+1子矩阵，为矩阵 d的第 d+1个对角线元素，为矩阵的 d+1阶顺序主子式，为第子矩阵，为矩阵 d的第个对角线元素，为矩阵的阶顺序主子式；

58、s842、根据分步骤s841中各子矩阵的特征值确定常对角矩阵的对角线元素；

59、s843、将分步骤s842中确定的对角线元素带入对应的常对角矩阵的等式，确定常对角矩阵，表示为：

60、

61、其中： d为以常对角矩阵为对角线元素的矩阵 ，为第1个跟随者的分布式控制律中的常对角矩阵，为第2个跟随者的分布式控制律中的常对角矩阵，为第个跟随者的分布式控制律中的常对角矩阵， nl为系统中引领者的个数，为跟随者的个数，。

62、进一步地，步骤s842包括以下分步骤：

63、s8421、确定常对角矩阵的第一对角线元素，使得第一子矩阵的第一特征值满足：

64、

65、其中：为第一子矩阵的第一特征值；

66、s8422、根据分步骤s8421中第一对角线元素和第一子矩阵的第一特征值确定第二对角线元素，使得第二子矩阵的第一特征值与第二特征值满足：

67、，

68、，

69、

70、其中：为第二子矩阵的第一特征值，为第二子矩阵的第一特征值，为第二子矩阵的第二特征值；

71、s8423、根据分步骤s8421和分步骤s8422进行迭代，确定第对角线元素，使得第子矩阵的特征值满足：

72、，

73、，

74、

75、其中：为第子矩阵的第特征值，为第子矩阵的第特征值，为第子矩阵的第特征值。

76、本发明的有益效果为：

77、（1）本发明可以在更为复杂的编队环境下，实现在精确的时间内对群体智能系统进行编队；

78、（2）本发明在协同控制目标编队构型过程中，使得编队在平移、以及放缩方面有着突出的优势。