一种针对机动目标的避障制导方法

本发明涉及一种针对机动目标的避障制导方法，属于避障制导方法。

背景技术：

1、为了提高拦截器的命中精度，几十年来提出了许多制导方法。然而，随着作战环境的日益复杂，目前的制导方法在以下情况下逐渐暴露出局限性：

2、1)在目标机动时实现精确制导。

3、2)在追击目标时避开地面障碍或敌人威胁。

4、对于前一种情况，针对机动目标提出了如下一些改进的制导方法：

5、增强比例导引律(augmented proportional navigation guidance,apng)、自适应滑模制导律(adaptive sliding-mode guidance,asmg)、最优制导律等，作为一种改进的比例导引律(proportional navigation guidance,png)，apng具有形式简单、实用性强的特点，它通过在png导引律中添加修正项来抑制目标机动对制导精度的影响[zarchanp.tactical and strategic missile guidance,sixth edition[m].reston,virginia:american institute of aeronautics and astronautics,inc.,2012:16-34.]。shen等人[shen j.research on generalized guidance law of anti-tactical ballisticmissiles[j].acta armamentarii,2015,36(s2):25-29.]推导出了两种apng形式，其中一种基于目标速度的法向加速度，另一种基于视线的角加速度(los)，然而，这两种形式都需要已知的精确目标机动信息。此外，apng无法克服传统png的缺点，即在制导的最后阶段所需的过载过大，这可能导致飞行过程中的姿态不稳定。asmg是一种基于变结构控制理论的新型制导方法，具有对参数摄动不敏感、抗外界干扰等优点。ji等人[ji h,liu x,song z,et al.time-varying sliding mode guidance scheme for maneuvering targetinterception with impact angle constraint[j].journal of the franklininstitute,2017,355(18):9192-9208.]提出了一种新的时变全局滑模控制技术，该技术使用线性扩展状态观测器来估计未知目标加速度，可以在期望的冲击角下实现机动目标拦截。文献[wang xx,lu h q,huang x l,et al.three-dimensional time-varying slidingmode guidance law against maneuvering targets with terminal angle constraint[j].chinese journal of aeronautics,2022,35(04):303-319.]的作者研究了在三维非解耦几何条件下拦截机动目标的问题，并开发了基于时基生成器函数的时变滑模控制方法。尽管已被证明是机动目标拦截的先进方法[lin c m,hsu c f.guidance law designby adaptive fuzzy sliding-mode control[j].journal of guidance,control,anddynamics,2002,25(2):248-256.]，[zhou d,mu c,xu w.adaptive sliding-modeguidance of a homing missile[j].journal of guidance control and dynamics,2015,22(4):589-594.]，asmg无法处理具有复杂约束的制导问题。这些约束来自于不同环境中的实际作战需求。

6、因此提出了基于最优控制理论的制导律。由于能够处理各种约束和目标，自[rusnak i,meir l.optimal guidance for acceleration-constrained missile andmaneuvering target[j].aerospace and electronic systems,ieeetransactionson.1990,26(4):618-624.]中推导出了针对机动目标的显式公式以来，最优制导律受到了广泛关注。此后，zhang等人[zhang q,wang z,tao f.optimal guidance lawdesign for impact with terminal angle of attack constraint[j].optik-international journal for light and electron optics,2014,125(1):243-251.]考虑了脱靶距离、冲击角、终端攻角等条件，并通过求解二次最优控制的riccati方程推导了最优制导律的一般公式。参考文献[kim y w,kim b,lee ch,et al.a unified formulationof optimal guidance-to-collision law for accelerating and deceleratingtargets[j].chinese journal of aeronautics,2022,35(07):40-54+3.]为具有任意加速度的目标提供了碰撞最优制导律的统一公式。weiss等人[weiss m,shima t.linearquadratic optimal control-based missile guidance law with obstacle avoidance[j].ieee transactions on aerospace and electronic systems,2019,55(1):205-214.]将最优制导理论扩展到拦截弹在击中目标之前必须避开空间区域的情况。然而，上述研究大多基于二维(2d)平面中的线性模型，这在很大程度上降低了问题的复杂性。此外，在导出全局最优制导律的过程中，由于系统干扰，终端时间很难估计，这极大地影响了制导精度。而在模型预测控制(modelpredictivecontrol,mpc)理论中，控制动作是通过在每个采样时刻求解有限时域开环最优控制问题而获得的，无需知道全局终端时间，因此mpc在解决最优制导问题方面具有优势。

7、然而，从目前的文献来看，mpc更多地用于对固定目标的制导。例如，在[shen k,wang j,li g,et al.optimal cooperative guidance law for salvo attack:an mpc-based consensus perspective[j].ieee transactions on aerospace&electronicsystems,2018,54(5):2397-2410.]中，提出了一种基于mpc的协同制导律，以对2d平面中的静止目标进行齐射攻击，在[zhao j,zhou s,zhou r.distributed time-constrainedguidance using nonlinear model predictive control[j].nonlinear dynamics,2016,84(3):1399-1416.]中，提出一种使用非线性mpc技术的多导弹网络的时间约束制导方法，这也可以实现2d平面中圆形禁飞区的避免。mpc作为一种能够抵抗外部干扰和系统不确定性的先进控制方法，有望进一步扩展到机动目标拦截的制导问题。对于后一种情况，无人机(uav)路径规划文献(han s c,bang h.proportional navigation-based optimalcollision avoidance for uavs[j].journal of institute of control robotics&systems,2004,10(11):1065-1070.xia l i,zhang j h,xie w j,et al.research onautonomic collision avoidance method for uav[j].flight dynamics,2011,29(6):48-51.chen h,chang k,agate c s.uav path planning with tangent-plus-lyapunovvector field guidance and obstacle avoidance[j].ieee transactions onaerospace and electronic systems,2013,49(2):840-856.)中对避障进行了很好的研究，但在制导研究中很少提及。这两种技术的本质区别在于，前者只需要引导无人机到达固定点，而后者则需要引导拦截器击中快速移动的目标。正是由于这种差异，无人机路径规划文献中的一些经典避障方法不能直接用于制导问题，例如人工势场(apf)方法[zhu l,cheng x,yuan fg.a 3d collision avoidance strategy for uav with physicalconstraints[j].measurement,2016,77:40-49.]。在apf中，无人机同时受到来自障碍物的排斥力和来自目标的吸引力的作用，其合力决定了无人机的飞行方向[guo y c,liu x x,zhang w g,et al.3d path planning method for uav based on improved artificialpotential field[j].journal of northwestern polytechnical university,2020,38(5):977-986.]。其中，吸引力确保了无人机在不被任何障碍物阻挡的情况下始终能够将其飞行方向对准目标点，这种保持飞行方向对准的方式在经典制导理论中也被称为速度跟踪制导律(velocity pursuit guidance law,vpgl)。然而，由vpgl引导的拦截器无法提前应对目标机动，当目标具有不亚于拦截器的机动能力时，这将最终导致拦截失败。同样，如果用于处理机动目标的制导问题，apf方法也将面临上述困难。

8、除上述之外，当前考虑障碍物回避的制导文献通常局限于2d平面[weiss m,shimat.linear quadratic optimal control-based missile guidance law with obstacleavoidance[j].ieee transactions on aerospace and electronic systems,2019,55(1):205-214.]、[zhao j,zhou s,zhou r.distributed time-constrained guidanceusing nonlinear model predictive control[j].nonlinear dynamics,2016,84(3):1399-1416.]、[zhao p,chen w,yu w.guidance law for intercepting target withmultiple no-fly zone constraints[j].the aeronautical journal,2017,121(1244):1479-1501.]，而在三维(3d)空间中，实际情况要复杂得多。大多数关于3d空间中避障的文献采用了简化障碍物模型的方法[khatib o.real-time obstacle avoidance formanipulators and mobile robots[j].international journal of robotics research,1986,5(1):90-98.]，例如将山、建筑物和敌方威胁建模为圆锥体、圆柱体、半球和其他规则几何结构[wang h l,lyu w t,yao p,et al.three-dimensional path planning forunmanned aerial vehicle based on interfered fluid dynamical system[j].chinesejournal of aeronautics,2015,28(01):229-239.]，这不仅提高了计算效率，而且很好地描述了障碍物的几何特征。即便如此，对于不同形状的障碍物，避障方法仍有很大差异。在[guo y c,liu x x,zhang w g,et al.3d path planning method for uav based onimproved artificial potential field[j].journal of northwestern polytechnicaluniversity,2020,38(5):977-986.]中，例如，最近点被集成到3d apf模型中，以确定排斥力的方向和大小，然而，对于不同形状的障碍物，计算最近点的方法是不同的。在[tan c y,huang s,tan k k,et al.three-dimensional collision avoidance for multiunmanned aerial vehicles using velocity obstacle[j].journal of intelligent&robotic systems,2020,97(1):227-248.]中，提出了一种专用于圆柱形障碍物的3d速度障碍物(velocity obstacle,vo)方法，可以作为对[jenie yi,van kampen e-j,de visser cc,et al three-dimensional velocity obstacle method for uncoordinatedavoidance maneuvers of unmanned aerial vehicles[j].guide.control dyn.2016,39(10),2312–2323.]中针对球形障碍物开发的3d vo方法的补充，但这两种方法都不适用于避开上述障碍物以外的其他障碍物。这些方法要求无人机提前识别障碍物的形状，并采取不同的方式来避免障碍物，这无疑增加了实施的难度。

9、最近提出的一种基于流体流动的方法可以处理不同形状的障碍物，同时考虑无人机的机动性约束[wang h l,lyu w t,yao p,et al.three-dimensional path planningfor unmanned aerial vehicle based on interfered fluid dynamical system[j].chinese journal of aeronautics,2015,28(01):229-239.]。然而，它通过在目标点放置一个下沉流来确保无人机飞到目的地，这在本质上与构建吸引力的方法相似，并将导致与apf方法在制导问题中遇到的同样的困难。

技术实现思路

1、本发明的目的是提供一种针对机动目标的避障制导方法。

2、本发明的一种针对机动目标的避障制导方法，其特殊之处在于包括以下步骤：

3、一种针对机动目标的避障制导方法，其特征在于包括以下步骤：

4、1)基于目标运动历史信息对目标机动造成的干扰进行估计，得到预测时域内的干扰估计值

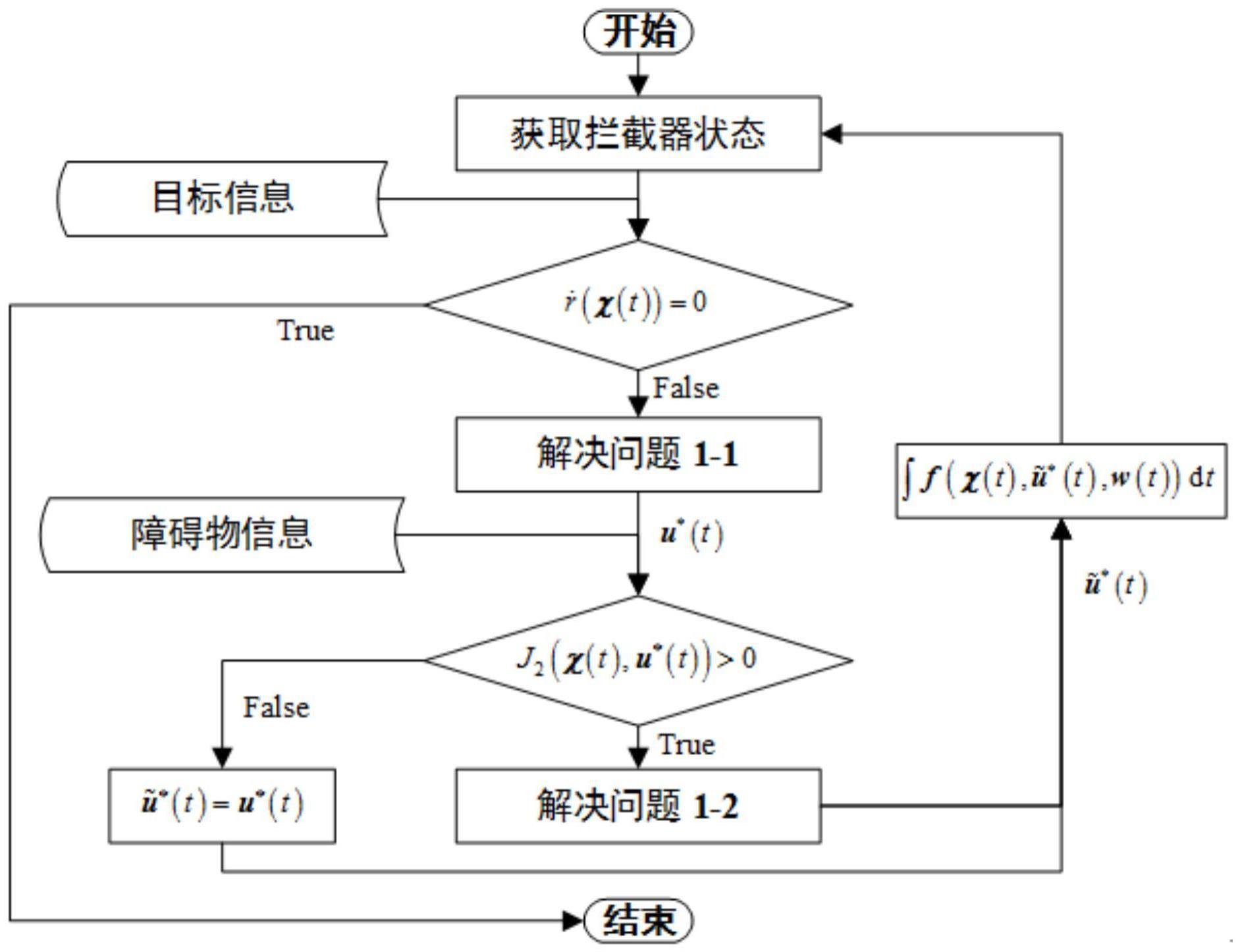
5、2)利用算法1求解有限时域最优控制问题1-1，得到最优制导指令u*(k)，问题1-1的目标函数1设计如式(27)所示；

6、

7、3)根据触发条件j2(u*(k))＝0判断u*(k)能否作为最终制导指令，若是，则令并转步骤5)，若否，则执行步骤4)，其中j2(·)如式(52)所示：

8、

9、4)利用算法2求解最优制导避障问题1-2，得到最优制导避障指令问题1-2的目标函数2定义为(53)；

10、

11、5)输出作为当前采样时刻拦截器制导指令，当时间到达下一采样时刻k+1，令k＝k+1并获取系统状态χ(k)，若有则停止制导，若否，则继续制导并重复上述步骤。

12、步骤1)中所述得到预测时域内的干扰估计值的步骤为：

13、首先，考虑到扰动无法直接观测，因此使用θt和ψt的前向差分代替，并将估计对象定义为

14、

15、其次，给定历史信息序列e(k-q),…,e(k-1),则e(k-q),…,e(k-1)与时间步1,…,q之间的函数关系可由非线性函数g(·)进行拟合

16、

17、根据拟合误差采取不同的方式进行估计，若拟合误差在指定范围内表明估计对象与时间有显著的相关性，则该函数可用于后续估计，并且有

18、

19、若拟合误差超出指定范围，表明函数g(·)不能很好地拟合上述关系，或者估计对象与时间之间的相关性很弱，那么基于估计对象在预测范围内保持不变的保守假设，只有最近的观测信息用于前馈补偿；

20、

21、上述估计方法可以表示为：

22、

23、考虑到多项式在逼近连续函数方面的良好性能，选择多项式函数来拟合上述关系，其系数由最小二乘法确定，具有优化系数的多项式函数写成

24、

25、其中，n-1是多项式函数的次数，系数α0(k),…,αn-1(k)将在每一采样时刻进行更新，确保观测信息得到充分利用。

26、目标函数1的推导过程如下：

27、拦截器和目标在惯性坐标系中的运动学方程分别为(1)和(2)。

28、

29、

30、其中，下标m和t分别代表拦截器与目标，其航迹倾斜角分别为θm和θt，航迹偏转角为ψm与ψt，空速为vm、vt。选择式(3)作为制导系统状态向量。

31、χ＝[xm,ym,zm,θm,ψm,xt,yt,zt,θt,ψt]t   (3)

32、则非线性系统可以由状态方程(4)、(5)进行描述:

33、

34、

35、其中是拦截器的控制输入，是目标机动形成的系统干扰；

36、零效脱靶量(zem)被定义为在目标继续沿其当前航向飞行且拦截器没有进一步修正机动的情况下，拦截器最终将错过目标的距离，在这种情况下，拦截器和目标之间的距离随时间的变化公式为(24)；

37、

38、从(24)可以看出，拦截器在之后将不再继续接近目标，因此zem可以确定为双方在tgo(χ)时的相对距离，根据二次函数的最值公式，该距离为

39、

40、并且有

41、

42、因此，基于zem的目标函数为

43、

44、步骤2)中所述有限时域最优控制问题1-1是给定系统状态χ(k)和估计值找到最优控制输入序列

45、

46、s.t.

47、

48、

49、步骤2)中所述算法1的具体步骤为：

50、step1初始化：设定算法参数k1,β1,β2,α，利用式(57)生成初始解u(0)(p；k)，初始化一阶、二阶有偏矩估计，以及迭代次数iter＝0；

51、

52、step2算法主循环：当时，执行step2.1～step2.4，否则执行step3

53、step2.1利用(41)，(42)计算j1(u(iter)(p；k))，利用(67)计算κ；

54、

55、step2.2利用(59)～(64)更新u(iter)(p；k)；

56、获取目标函数的梯度

57、

58、更新有偏一阶矩估计值

59、η(iter)＝β1η(iter-1)+(1-β1)g(iter)   (60)

60、更新有偏二阶矩估计值

61、ν(iter)＝β2ν(iter-1)+(1-β2)g(iter)⊙g(iter)   (61)

62、计算无偏一阶矩估计值

63、

64、计算无偏二阶矩估计值

65、

66、更新u(iter)

67、

68、其中，对于向量的所有运算都是逐元素进行的，β1,β2∈(0,1]是矩估计的衰减率，α∈(0,1]是步长，是一个小的正有理数。初始有偏矩估计值满足

69、此外，为了使满足迭代过程中的控制输入约束，引入了非线性饱和函数sat(·)：

70、

71、step2.3利用(66)修正u(iter)(p；k)；

72、

73、step2.4更新当前迭代次数为iter＝iter+1；

74、step3利用(70)确定最优解u*(p；k)，取其首个分量作为u*(k)；

75、

76、步骤3、步骤4)中的触发条件以及目标函数2的推导过程如下：

77、为了在制导过程中避免地面障碍或空间区域，首先需要一种有效的建模方法，所有检测到的障碍物或敌方威胁区域都被视为可以适当包围它们的规则几何体，统一模型用公式(7)、(8)来描述；

78、为了便于表达，所有障碍物、威胁区域和它们被视为的规则几何形状统称为障碍物；

79、

80、其中是障碍物集合，(zoi,xoi)是障碍物oi的几何中心在zox上的投影,参数向量ωi决定oi的形状，并且有：

81、

82、考虑到拦截器在惯性坐标系中的运动，如果拦截器没有进一步机动，根据式(7)，γi的变化将如公式(44)所示；

83、

84、这里，t的可行范围是(45).

85、

86、从(45)中可以注意到，除了将拦截器的飞行高度限制在拦截器可能与障碍物碰撞的范围内的现有约束之外，还应针对拦截器在遇到障碍物之前击中目标的情况施加额外的约束，即t＜tgo(χ)；

87、令

88、

89、则有

90、

91、定义单个障碍的威胁函数为(48)

92、

93、拦截器沿当前航向进入障碍物的深度越深，障碍物的威胁就越大，如果拦截器在没有进一步机动的情况下未与障碍物相撞，障碍物威胁则为零，然而，由于t的可行范围涉及不同的情况，公式(48)中的很难确定，参见下述内容：

94、威胁函数和代价函数的解析表达式

95、为了获得的确切值，将与相关的所有可能情况总结如下：

96、

97、然后，根据一元二次函数的极值点与可行区间的端点之间的关系，可以分段形式表示为(50)；

98、

99、令

100、

101、其中为一较大正有理数。这样，ζi(χ,ωi)在任何可能情况下的取值可由(49)，(50)，(51)和(48)确定；

102、避障的总代价被视为来自所有探测到的障碍物的威胁总和，即(52)，使用下一采样时刻的预测系统状态，问题1-2的目标函数可以定义为(53)；

103、

104、

105、此处，通过式(40)取得；

106、基于预测系统状态可通过递推获得

107、

108、其中

109、步骤4)中所述最优制导避障问题1-2是给定系统状态χ(k)、估计值以及求解问题1-1获得的制导指令u*(k)，找到最优避障-制导指令

110、

111、s.t.

112、

113、j2(χ(k),u*(k))＞0     (56)。

114、步骤4)中所述算法2的具体步骤为：

115、step1初始化：设定算法参数k1,β1,β2,α，利用(58)生成初始解

116、

117、step2对于种群中的任意个体，初始化其一阶、二阶有偏矩估计，以及迭代次数iter＝0，

118、当时，执行step2.1～step2.4，否则执行step3；

119、step2.1利用(41)，(42)计算利用(67)计算κ；

120、

121、s.t.

122、

123、

124、step2.2利用(59)～(64)更新

125、获取目标函数的梯度

126、

127、更新有偏一阶矩估计值

128、η(iter)＝β1η(iter-1)+(1-β1)g(iter)   (60)

129、更新有偏二阶矩估计值

130、ν(iter)＝β2ν(iter-1)+(1-β2)g(iter)⊙g(iter)   (61)

131、计算无偏一阶矩估计值

132、

133、计算无偏二阶矩估计值

134、

135、更新u(iter)

136、

137、其中，对于向量的所有运算都是逐元素进行的，β1,β2∈(0,1]是矩估计的衰减率，α∈(0,1]是步长，是一个小的正有理数。初始有偏矩估计值满足

138、step2.3利用(66)修正

139、

140、step2.4更新当前迭代次数为iter＝iter+1；

141、step3利用(70)确定个体最优利用(71)确定全局最优解

142、

143、

144、本发明一种针对机动目标的避障制导方法，解决了具有避障要求的机动目标的三维制导问题，利用优化技术、mpc理论和几何方法的新型制导方法。主要有益效果如下：

145、(1)将最优制导问题中的避障约束转化为具有触发条件的独立优化问题，在此基础上提出了避障制导的总体方案；

146、(2)提出了一种改进目标函数和干扰估计器的mpc制导方法，以确保拦截器在无需避开任何障碍物的情况下能够精确命中目标；

147、(3)基于vo模型和简化的障碍物几何结构，推导了不同形状障碍物威胁函数的统一表达式，构建了用于防撞和制导的目标函数；

148、(4)针对制导避障问题，设计了自适应矩估计(adam)算法，其解将作为拦截器的实时制导指令。