一种针对非机动目标的航天器追逃防博弈控制方法

本发明属于航天器，具体涉及一种针对非机动目标的航天器追逃防博弈控制方法。

背景技术：

1、在轨航天器容易受到非合作目标的攻击与抵近，由于其价值高燃料需要用于在轨工作，因此在受到威胁时不能自主躲避，需要释放伴随卫星作为防御星进行协同对抗。防御星与追击星之间对于主星的位置争夺就称为针对非机动目标的航天器追逃防博弈控制问题，追击星的目的是靠近主星，同时又要保证自身不被防御星拦截破坏；防御星的目的是尽可能避免追击星靠近主星。

2、目前对航天器追逃防博弈控制问题的建模与求解大部分使用非零和微分对策方法，但由于其属于博弈类型中的非零和博弈，追击星和防御星的代价函数并不相同，因此对其最优控制策略的求解往往非常复杂，且最终都转化为两点边值问题进行数值求解，耗时很长且精度不高，导致不能及时控制防御星的运行路径，使得位于主星周围的防御星无法及时阻止追击星的靠近主星。

技术实现思路

1、为了克服现有技术中的博弈问题存在的对于最优控制策略的求解复杂，且最终都转化为两点边值问题进行数值求解，耗时很长且精度不高，导致主星周围的防御星无法及时阻止追击星的靠近主星的问题。本发明的目的在于提供一种针对非机动目标的航天器追逃防博弈控制方法，将追击星和防御星的博弈目的通过一对数值相反的代价函数描述，使得求解过程大大简化，耗时短的同时快速控制防御星的运动轨迹，使得防御星具有更强的机动能力，拦截追击星更加精确。。

2、为达到上述目的，本发明采用了以下技术方案：

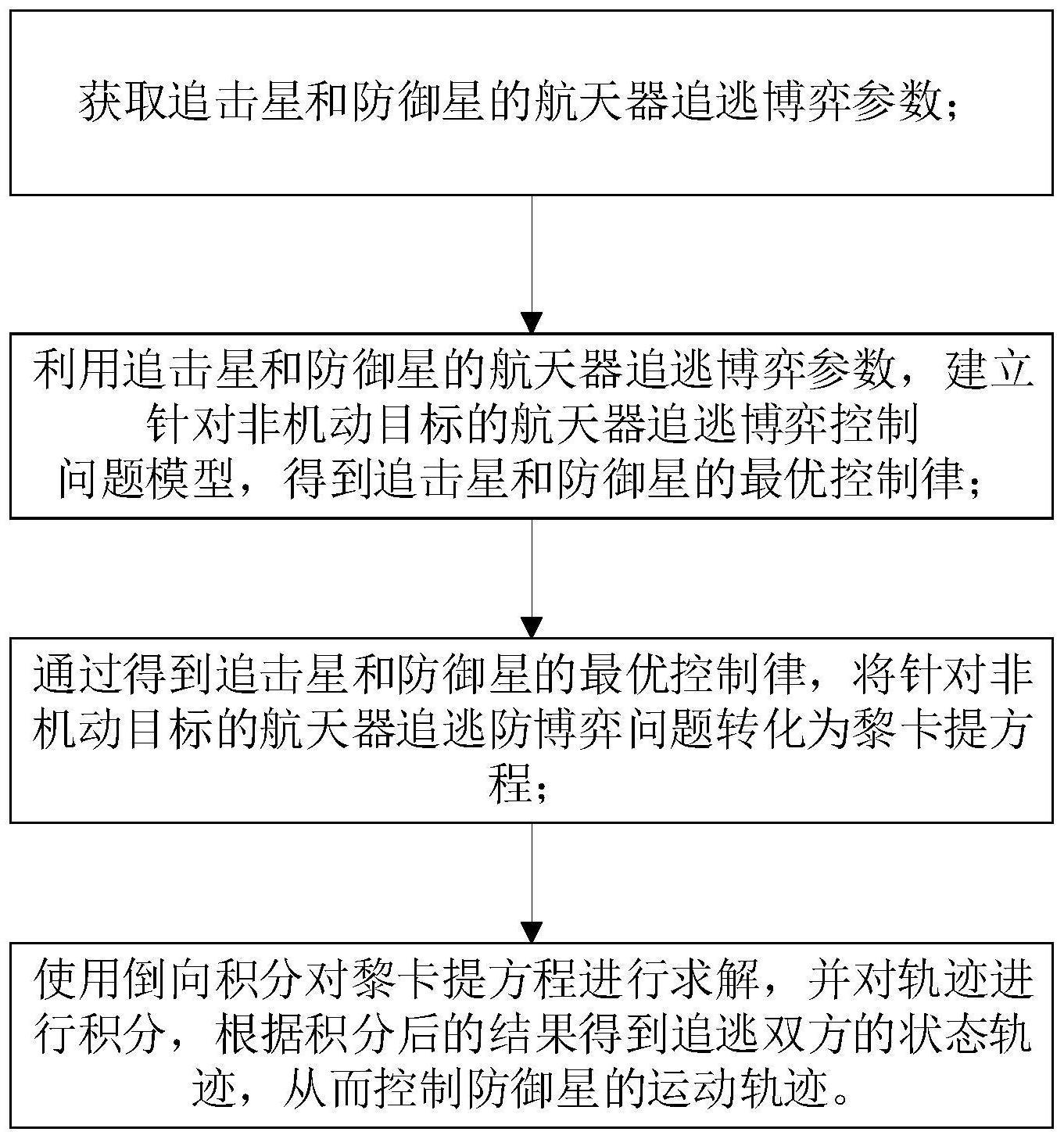
3、一种针对非机动目标的航天器追逃防博弈控制方法，包括：

4、获取追击星和防御星的航天器追逃博弈参数；

5、利用追击星和防御星的航天器追逃博弈参数，建立针对非机动目标的航天器追逃博弈控制问题模型，得到追击星和防御星的最优控制律；

6、通过得到追击星和防御星的最优控制律，将针对非机动目标的航天器追逃防博弈问题转化为黎卡提方程；

7、使用倒向积分对黎卡提方程进行求解，并对轨迹进行积分，根据积分后的结果得到追逃双方的状态轨迹，从而控制防御星的运动轨迹。

8、作为本发明的进一步改进，所述获取追击星和防御星的航天器追逃博弈参数，其中：

9、追击星和防御星的航天器追逃博弈参数包括追击星的初始位置，防御星的初始位置，追击星的速度，防御星的速度。

10、作为本发明的进一步改进，所述建立针对非机动目标的航天器追逃博弈控制问题模型，包括：

11、以主星t的位置为原点建立lvlh坐标系，基于lvlh坐标系结合追击星和防御星的航天器追逃博弈参数设计代价函数；

12、基于cw方程，确定在空间轨道上追击星和防御星所需要满足的动力学约束的微分方程；

13、根据上述过程完成基于微分对策建立的针对非机动目标的航天器追逃防博弈模型。

14、作为本发明的进一步改进，所述以主星t的位置为原点建立lvlh坐标系，基于lvlh坐标系结合追击星和防御星的航天器追逃博弈参数设计代价函数，包括：

15、

16、该代价函数分为终端项和积分项两部分：

17、终端项的含义是终端时刻追击星和主星之间的相对状态与防御星和主星之间的相对状态；积分项的含义是整个博弈过程中双方的燃料消耗；

18、其中，ja为追击星的代价函数；jd为防御星的代价函数；xa为追击星的状态矢量；xd为防御星的状态矢量；tf为博弈的终端时刻；q1为追击星-主星终端距离项的权重矩阵；q2为防御性-追击星终端距离项的权重矩阵；ra为追击星燃料消耗项的权重矩阵；rd为防御星的燃料消耗项的权重矩阵；ua为追击星施加的连续控制量；ud为防御星施加的连续控制量。

19、作为本发明的进一步改进，所述得到追击星和防御星的最优控制律，包括：

20、基于拉格朗日乘子法引入协态变量，将有微分方程等式约束的双边优化问题转化为无约束双边优化问题，对代价函数进行处理得到辅助代价函数：

21、

22、其中：xa为追击星的状态矢量；tf为博弈的终端时刻；y为防御星和追击星的状态差；q1为追击星-主星终端距离项的权重矩阵；q2为防御性-追击星终端距离项的权重矩阵；ra为追击星燃料消耗项的权重矩阵；rd为防御星的燃料消耗项的权重矩阵；ua为追击星施加的连续控制量；ud为防御星施加的连续控制量；λ为引入的拉格朗日乘子；v为引入的第二个拉格朗日乘子。

23、作为本发明的进一步改进，所述对代价函数进行处理得到辅助代价函数，之后对辅助代价函数求变积分：

24、

25、其中：

26、

27、

28、其中：λ(t)为引入的拉格朗日乘子；ν(t)为引入的第二个拉格朗日乘子；xa为追击星的状态矢量；xd为防御星的状态矢量；ua为追击星施加的连续控制量；ud为防御星施加的连续控制量；为终端约束函数；h为哈密尔顿函数；

29、得到，追击星和防御星的最优控制律：

30、

31、

32、其中：ra为追击星燃料消耗项的权重矩阵；rd为防御星的燃料消耗项的权重矩阵；ua为追击星施加的连续控制量；ud为防御星施加的连续控制量；λ(t)为引入的拉格朗日乘子；v(t)为引入的第二个拉格朗日乘子。

33、作为本发明的进一步改进，所述将针对非机动目标的航天器追逃防博弈问题转化为黎卡提方程求解问题，包括：

34、将追击星和防御星的最优控制律代入追击星和防御星的动力学约束微分方程：

35、

36、根据上述动力学约束方程得到联合状态向量与联合协态变量之间的关系如下：

37、

38、根据横截条件得到联合状态向量和联合协态变量的终端关系：

39、

40、联合状态向量与联合协态变量之间存在线性关系：

41、λ(t)＝p(t)k(t)

42、两边同时求导得：

43、

44、联立公式和得：

45、

46、其中：q1为追击星-主星终端距离项的权重矩阵；q2为追击星-主星终端距离项的权重矩阵；xa为追击星的状态矢量；ra为追击星燃料消耗项的权重矩阵；rd为防御星的燃料消耗项的权重矩阵；λ(t)为引入的拉格朗日乘子；v(t)为引入的第二个拉格朗日乘子；p(t)为联合状态向量与联合协态向量的关系矩阵；tf为博弈的终端时刻。

47、作为本发明的进一步改进，所述将针对非机动目标的航天器追逃防博弈问题转化为黎卡提方程求解问题，该问题的解为：

48、

49、

50、其中：ud为防御星施加的连续控制量；ud为防御星施加的连续控制量；ra为追击星燃料消耗项的权重矩阵；rd为防御星的燃料消耗项的权重矩阵；sa为追击星控制转换矩阵；sd为防御星控制转换矩阵；k(t)为联合协态变量。

51、作为本发明的进一步改进，所述使用倒向积分对黎卡提方程进行求解，包括：

52、以黎卡提方程的终值为起点，对微分方程取负：

53、

54、作为本发明的进一步改进，所述使用倒向积分对黎卡提方程进行求解，并对轨迹进行积分，其中对轨迹进行积分是使用积分算法进行积分，得到矩阵p(t)。

55、与现有技术相比，本发明具有以下有益效果：

56、本发明一种针对非机动目标的航天器追逃防博弈控制方法，通过获取追击星和防御星的航天器追逃博弈参数，建立针对非机动目标的航天器追逃博弈控制问题模型，通过得到追击星和防御星的最优控制律，将针对非机动目标的航天器追逃防博弈问题转化为黎卡提方程求解问题，使用倒向积分对黎卡提方程进行求解。同时，本发明为采用主从星协同的航天器，提供有效的威胁解决方案。本发明建立的针对非机动目标的航天器追逃博弈控制问题模型，是基于线性的cw方程的一种微分对策博弈模型，具有模型简单，线性化误差很小的优点，根据本发明给出的追逃防博弈问题求解方法，可以将复杂的非零和博弈问题转化为了零和博弈问题，并进一步转化为了黎卡提方程求解问题，显著提升了求解效率，缩短了求解时间，快速得到追逃双方的状态轨迹。当在轨执行原有任务的主星被追击星企图靠近的时候，根据得到追逃双方的状态轨迹，可以及时调整主星周围的防御星的状态轨迹，控制主星周围的防御星及时对追击星进行拦截，避免追击星靠近主星。使得防御星具有更强的机动能力，拦截追击星更加精确。