基于多智能体理论的自动驾驶车辆底盘分布式协同控制方法及控制器

本发明属于自动驾驶汽车轨迹跟踪领域，尤其涉及一种基于多智能体系统的底盘协同控制方法及控制器。

背景技术：

1、随着社会经济的发展，汽车产业逐渐成为国民支柱产业。但汽车数量的快速增长也带来了越来越多的问题，如交通安全、能源紧张和环境污染等问题。而车辆电气化、智能化和线控化的发展方向为解决上述问题提供了有力的技术支持。尤其在车辆主动安全领域，底盘线控化取消了不同车轮转向执行器与驱动执行器之间的机械连接，转而采用灵活的线束布置，使得越来越多的主动安全技术有能力应用在车辆上。如主动前轮转向(afs)通过在汽车转向过程中叠加一个附加前轮转角来改变轮胎侧向力，产生补偿横摆力矩，保证汽车的稳定性。直接横摆力矩控制(dyc)通过分布式驱动车辆的转矩矢量控制产生维持车辆稳定性所需的附加横摆力矩。四轮转向技术(4ws)采用两种不同的转向模式，通过反向转向方式提高操纵灵活性并减少转弯半径，而通过同向转向的方式提高高速下的侧向稳定性。

2、同时，通过将转向系统、驱动/制动系统与悬架系统的集中式协同控制，可以进一步提高车辆的操稳性与舒适性。但目前的控制方案大多采用集中式的策略，由统一的控制器对所有控制量进行求解。该种控制策略存在着以下问题。(1)随着底盘功能的复杂化，越来越多的系统加入协同控制的范围。这势必造成控制量的增多，增加了控制器的计算负担；(2)集中式的控制策略在控制器硬件失效的情况下将造成整个系统的崩溃。若使用备用控制器的系统冗余方案，则又将大大增加整车的成本；(3)普通mpc控制器在对未来状态进行预测求解后，仅取控制序列的第一列作为控制量输入车辆，造成了极大地数据浪费。

3、因此，本发明针对上述急需解决的问题，提出了一种基于多智能体系统(mas)的底盘分布式协同控制方法，依据图论构建mas的拓扑关系。通过分布式模型预测控制(dmpc)计算单一智能体的控制量，合理设计dmpc的成本函数，引入一致性控制理论。通过拉普拉斯矩阵确定不同智能体间的权重，实现了相邻智能体误差同时收敛至零的目标，避免系统出现震荡，降低了控制器的计算负担，提高了行驶安全性。

技术实现思路

1、本发明针对具有四轮驱动与四轮转向的自动驾驶汽车，提供了一种在双移线工况下的车辆底盘协同控制方法，该方法通过预瞄前方道路信息和合理设计集成控制算法实现了车辆的跟踪性能与操纵稳定性，解决了现有技术存在的不足。本发明的技术方案如下：

2、s1：二自由度车辆是一类较为经典的车辆模型，其在建模的过程中忽略了悬架的作用，认为汽车车身只作平行于地面的平面运动，同时将汽车的纵向速度视为不变，如图1所示。通过上述的简化，使得该模型能够较直观的展示出车辆的横向运动，如下式所示：

3、

4、

5、式中，m为车辆质量，iz为绕z轴的转动惯量，vx和vy为车辆的纵向和横向速度，r是横摆角速度。lf和lr分别为车辆质心到前轴和后轴的距离，l＝lf+lr。cαf和cαr分别为前后轮胎的横向刚度。δf为前轮转角，β为车辆质心侧偏角。当公式(1)-(2)的等号左边都为零时，车辆处于稳定状态，联立两公式可得到期望的横向速度和横摆角速度：

6、

7、

8、s2：本发明的研究对象为具有四轮转向与四轮驱动的自动驾驶车辆，其复杂的非线性动态特性使得二自由度车辆模型无法精确地描述车辆的运动状态。因此，控制器采用更为精确的七自由度车辆模型。如图2所示，该模型考虑了车辆的纵、横向运动、横摆运动以及四个车轮的滚动，并同时忽略了垂向运动。七自由度模型的动态方程可表达如下：

9、

10、

11、

12、

13、fxi,fyi(i＝fl,fr,rl,rr)为轮胎力在车辆坐标系x-y下的投影，而下标i＝fl,fr,rl,rr分别代表了左前、右前、左后和右后。jwi和ωi为四个车轮的转动惯量和旋转角速度，ti为车轮的制动/驱动力矩，rw为车轮的滚动半径，d为轮距。根据小角度假设sinθ≈tanθ≈θ,cosθ≈1，则fxi,fyi可以表示为：

14、

15、式中，fti和fsi为轮胎纵向力和侧向力，δi为车轮转角，i＝fl,fr,rl,rr。同时，该模型考虑车辆行驶中的载荷转移，其对轮胎的附着极限有着重要的影响：

16、

17、式中，fzi为车轮垂直载荷，g为重力加速度，hg为车辆重心高度。作为车辆与路面的唯一接触对象，轮胎力的变化对车辆的操纵稳定性有着较大的影响，魔术公式作为经过大量实验数据得到的经验模型，拟合精度很高，具有较强的统一性，可通过一套公式来表达轮胎的纵向力和横向力，使用较为方便。同时，公式中的参数也较容易获得。在纯滑移/纯侧偏工况下，其计算公式如下：

18、

19、其中，bt,bs分别是纯滑移/纯侧偏刚度因子，ct,cs分别是纯滑移/纯侧偏形状因子，dt,ds分别是纯滑移/纯侧偏峰值因子，et,es分别是纯滑移/纯侧偏曲率因子。ftp为纯滑移工况下的轮胎纵向力，fsp为纯侧偏工况下的轮胎横向力。然而，在实际行驶过程中，轮胎通常处于滑移+侧偏的复合工况下。此时，轮胎纵向力与横向力之间产生了复杂的非线性耦合作用，纯滑移/侧偏条件下的轮胎模型显然无法准确描述。因此，针对复合工况下的改进型魔术公式被提了出来，该工况下的轮胎力可由下式获得：

20、

21、其中，

22、

23、式中，s和α为轮胎滑移率和轮胎侧偏角，ft为复合工况下的轮胎纵向力，fs为复合工况下的轮胎横向力。基于车轮动力学的分析，轮胎滑移率和侧偏角由下式得到：

24、

25、

26、式中，vti是每个车轮的轮心处的纵向速度，i＝fl,fr,rl,rr，可由下式计算得到：

27、

28、s3：建立预瞄跟踪模型模拟驾驶员在行驶中对已知轨迹的决策和对自身及汽车动力学特性的掌控，通过该模型计算得到期望前轮转角δdes，并由此根据公式(3)和(4)计算期望的横摆角速度rdes和横向速度vydes。该预瞄跟踪模型如图3所示。

29、其中，x-y为大地坐标系，(xo,yo)为车辆当前时刻的位置，(xk,yk)为预瞄点坐标，lp为预瞄距离。ey为横向跟踪误差，可由下式计算得到：

30、

31、为车辆航向角，根据预瞄跟踪理论和恒定横摆角速度假设，将车辆的横向位移进行泰勒展开：

32、

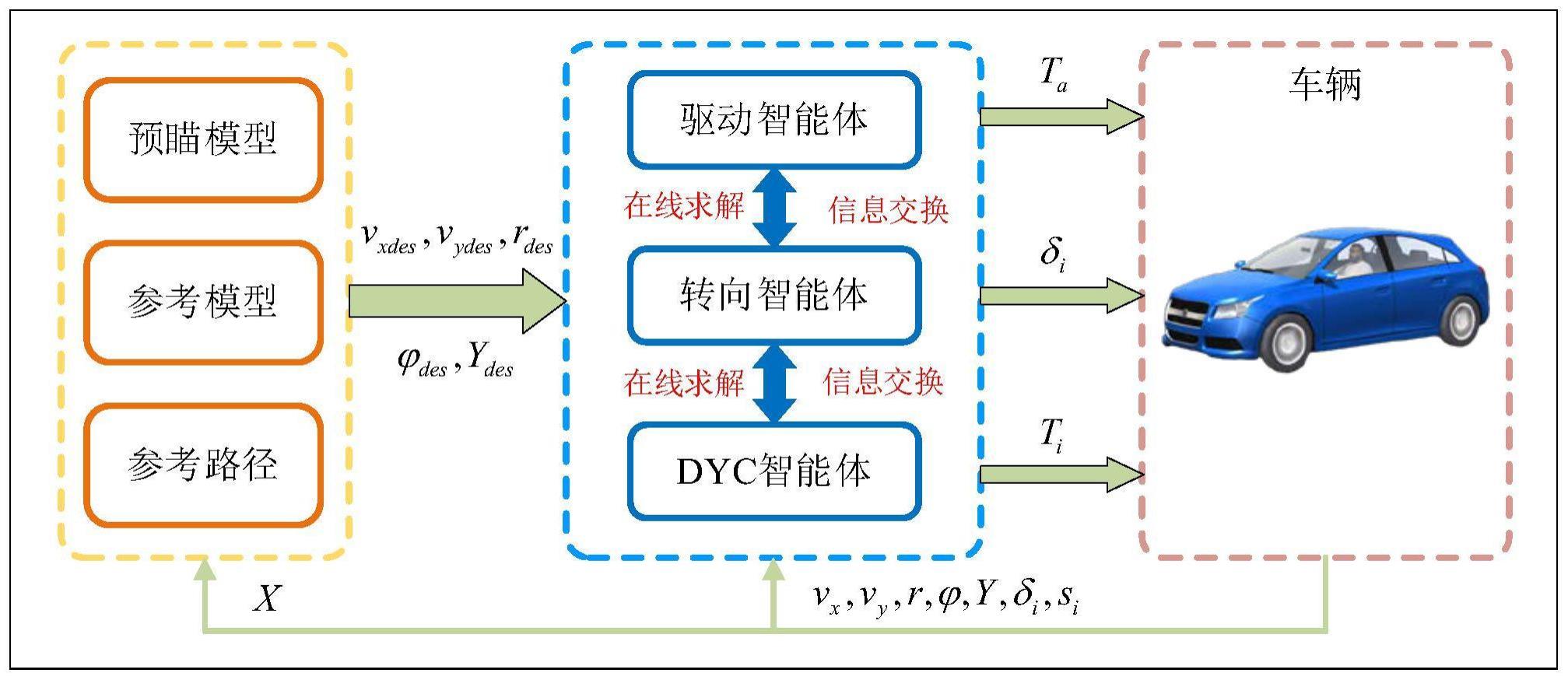
33、其中，δt为预瞄时间。根据路径跟踪的最小误差原则，在行驶δt时间后，当车辆轨迹正好经过预瞄点(xk,yk)时，行驶轨迹即为最优轨迹曲率。结合式(18)可得最优曲率为

34、

35、式中，r*为最优曲率半径。

36、此外，根据车辆运动学原理，质心处的横摆角速度为r＝vx/r*，并联立公式(3)、(19)，即可得到预瞄模型输出的期望前轮转角

37、

38、s4：构建基于图论的多智能体系统架构。在多智能体系统理论研究中，图论是一个重要的研究基础工具。每个智能体与其他智能体之间的信息交流可以通过图论清晰地表示出来。为充分发挥多智能体系统的长处，减少分布式计算时间，提高系统安全冗余度，将四轮转向/四轮驱动车辆的底盘控制动作分为三个智能体，分别是驱动智能体，转向智能体和dyc智能体，并构建了如图4所示的拓扑结构。

39、驱动智能体的输出量为驱动力矩ta，其以相等的数值作用在四个车轮上，负责实现对期望纵向速度的跟踪。转向智能体的输出量为四个车轮的转角δi，负责提高路径跟踪的精度。dyc智能体的输出量为四个车轮的转矩ti，通过转矩差形成控制车辆横摆运动的直接横摆力矩，负责控制车辆的稳定性，防止车辆失稳。其与驱动智能体的输出量ta相加，共同作用在车轮上。

40、本发明所提多智能体系统的邻接矩阵a、入度矩阵d和拉普拉斯矩阵l分别为：

41、

42、s5：dmpc算法的提出是为了解决相互独立子系统之间并行计算的问题，也适用于多智能体系统中的子智能体之间的协调与合作。通过交换状态信息，可以实现每个子智能体的并行计算。使得系统具有良好的可扩展性，便于实现车辆底盘系统“即插即用”的功能，降低了不同功能车型之间的软硬件匹配成本。同时，dmpc可以将多目标优化问题转化为相互独立的单目标优化问题，很大程度上降低了系统的耦合性以及计算的复杂度。整个控制算法架构如图5所示。

43、本发明所提多智能体协同控制系统主要对vx,vy,r,y五个变量实现跟踪。其中，期望航向角和期望纵向位移ydes可由下式计算得到：

44、

45、其中，

46、

47、假设质心侧偏角足够小，即认为航向角约等于横摆角。并结合公式(5)-(7)，对其进行适当的改写即可得到车辆非线性状态方程为

48、

49、其中，ta为驱动智能体的控制变量驱动转矩，状态变量为控制变量为u＝[ta,δfl,δfr,δrl,δrr,sfl,sfr,srl,srr]t。为减轻计算负担，利用一阶泰勒展开，实现状态方程的线性化。得到状态矩阵和控制矩阵分别为

50、

51、随后，对该连续系统状态方程做离散化处理

52、

53、其中，ad＝i+ta*,bd＝tb*,cd＝diag(1,1,1,1,1)，η(k)为离散化处理后的状态输出矩阵，t为控制系统的采样周期，i为单位矩阵。

54、结合式(24)，(26)和本发明提出的多智能体结构，建立对应的多智能体系统方程如下

55、

56、其中，i＝1,2,3，分别代表驱动智能体、转向智能体和dyc智能体。式(27)中，ai＝ad，bi1＝bd(1,:)，表示将bd矩阵的第1行赋值给bi1，u1＝[ta]，c1＝diag(1,0,0,0,0)。bi2＝bd(2:5,:)，表示将bd矩阵的第2至5行赋值给bi2，u2＝[δfl,δfr,δrl,δrr]t，c2＝diag(0,0,0,1,1)。bi3＝bd(6:9,:)，表示将bd矩阵的第6至9行赋值给bi3，u3＝[sfl,sfr,srl,srr]t，c3＝diag(0,1,1,0,0)。

57、令预测时域np与控制时域nc均为n，则对于第i个子智能体系统，其最优控制变量序列可表示为：

58、ui(k)＝[ui(k+1|k),ui(k+2|k),…,ui(k+j|k)]t,j＝0,1,…,n-1    (28)

59、ui(k+j|k)表示为在k时刻对未来k+j时刻的控制量的计算。

60、在传统集中式mpc的滚动优化过程中，通常将求解得到的最优控制序列中的第一项作为控制变量，而将其他最优控制变量直接舍弃，这导致了控制器计算资源和计算数据的浪费。而对多智能体系统来说，各子智能体需要独立的计算求解变量。为了提高数据利用的效率，考虑采用上一时刻的其他智能体的最优控制序列来构造当前时刻的相邻未来控制变量序列。以智能体1为例，其相邻智能体的最优控制序列分别为：

61、

62、将k＝0的控制量作用于系统，并交换彼此的最优控制序列，将相邻智能体的未来控制量作为已知信息代入式(27)中进行计算。须注意到，相邻智能体的未来控制变量变为

63、

64、控制变量序列的范围减少到1～n-1时刻，其与控制时域n的长度不匹配。为解决该问题，对终端控制输入采用局部静态反馈的方法进行求解。在这种方法中，控制器的输出仅取决于当前状态的局部范围内的状态变量，而且控制律以线性形式表示。假设三个智能体n-1时刻的控制变量为

65、ui(k+n-1|k),i＝1,2,3    (31)

66、将其代入式(27)即可得到n时刻的预测状态η(t+n|t)。使用代数黎卡提方程(algebraic riccati equation，are)对最优状态反馈控制器矩阵k进行求解。are是一种以矩阵形式表现的非线性代数方程，用于描述线性时不变系统的最优状态反馈控制器。构建形式如下的are

67、pa+atp-pbr-1btp+q＝0    (32)

68、其中，a＝ad,b＝bd。p是待求解的对称半正定矩阵，q和r为权重矩阵。利用matlab的idare命令对p矩阵进行求解。则反馈增益矩阵为k＝r-1btp。并可得到n时刻的终端输入变量为

69、ui(k+n|k)＝k*η(k+n|k),i＝1,2,3    (33)

70、将其补至未来控制变量的末端，得到三个智能体对应的控制序列为

71、ui(k)＝{ui(k+1|k),ui(k+2|k),…,ui(k+n-1|k),k*η(k+n|k)}    (34)

72、结合公式(27)，对dmpc的迭代过程进行递推得到：

73、

74、将上述迭代过程写成如下的增广矩阵的形式：

75、γi＝ψiξi(k)+θiu    (36)

76、

77、

78、

79、其中，γi是输出增广向量，u是输入增广向量，ψi和θi分别是状态增广矩阵和控制增广矩阵。考虑各智能体的参考输出向量为：

80、γides＝[ξides(k+1) ξides(k+2)…ξides(k+n)]t    (40)

81、构建如下各子智能体成本函数：

82、

83、其中，qi1，qi2和qi3分别为权重矩阵。aij是邻接矩阵a的元素。ei为各智能体的跟踪误差：

84、

85、同时，各智能体的控制量还应受到对应的执行器动作约束和车辆动力学约束，具体表现为：

86、

87、式中，umin,umax分别为执行器的最小/最大动作量，μ为路面附着系数。

88、s6：将dmpc的滑移率控制量转化为驱动/制动力矩；

89、s7：将所求得的力矩和转角发送给底盘执行单元执行。

90、本发明的有益效果：

91、1、依据图论构建智能体系统的拓扑关系，通过拉普拉斯矩阵确定不同智能体间的权重。同时，利用mas一致性控制的理论基础，设计各dmpc控制器的成本函数。使相邻智能体误差同时收敛至零，避免出现震荡现象；

92、2、针对dmpc终端控制序列与状态序列未知的问题，引入局部静态反馈的方法。通过求解代数riccati方程得到状态反馈增益，对终端控制序列和状态序列进行求解和预测，避免了控制求解精度低的问题；

93、3、本发明所提分布式控制方法降低了每个控制器的计算负担，减少了计算时间。较集中式控制方法，避免了单一控制器失效而导致的车辆失稳的现象，提高了整个系统的安全冗余度。