一种非完整机器人编队的有限时间事件触发容错控制系统

本发明涉及非完整多机器人编队控制领域，尤其涉及一种非完整机器人编队的有限时间事件触发容错控制系统。

背景技术：

1、随着信息量的增大，移动机器人的任务越来越艰巨，单个移动机器人往往不能高效地完成任务，因此编队控制作为多机器人协同控制中典型代表，在实际工程中被广泛应用，通过多个移动机器人的相互作用形成某种几何结构去执行任务，大大提高了工作效率。非完整机器人作为轮式移动机器人的典型代表，其结构简单、运动灵活、存在欠驱动性质。非完整多机器人编队是考虑环境感知、信息交流、动态决策、运动执行等多种因素的一类复杂控制模型，因此非完整多机器人编队控制成为了一个重要的研究方向。

2、在复杂的编队控制中，首先要考虑机器人自身安全和通信设备探测范围的限制问题，主要是为了保证机器人在有效交流范围内进行信息传输并且相互之间不发生碰撞。其次，执行器故障问题同样会影响系统的安全问题，一旦发生故障从系统将不受控制从而发生碰撞问题，所以在出现执行器故障时，保证系统的正常运行和编队的正常控制是尤为重要且非常具有实际意义的。目前，有很多控制技术应用到了非完整多机器人编队的控制上面。但是，现有技术仍然存在以下问题：

3、第一，在现有的非完整多机器人编队控制方法中，大多没有考虑无限次间接性未知执行器故障的容错控制问题。如果这些未知故障不能被很好地补偿，单个机器人的故障可能会迅速蔓延到整个系统，破坏系统稳定性，使每个机器人失去控制，进而不能保持正常的编队结构，使机器人之间发生碰撞。第二，在现有的非完整多机器人编队控制方法中，大多没有考虑信息传输过程中网络资源的浪费问题。当系统存在未知执行器故障时，被控对象不仅需要不断地接收领导者的信息而且需要对未知故障进行观测和补偿，控制器会连续不断地向执行器输入信号，从而导致资源的大量浪费。第三，在现有的非完整多机器人编队控制方法中，大多没有考虑系统参数和动力学中未知函数的不确定问题。从实际角度来看，系统模型中的某些部分可能会由于不同路况等环境的改变和机器人部件磨损而发生变化，所以有必要研究这些不确定因素对系统的影响。第四，在现有的非完整多机器人编队控制方法中，大多没有考虑避碰和连通性保持问题。而从实际角度来看，考虑有限的信号检测范围和安全的跟踪范围，所以要求跟随者要根据领导者的信息做出相应的调整，从而使两者保证在有效的交流范围内防止发生碰撞。

技术实现思路

1、本发明提供一种非完整机器人编队的有限时间事件触发容错控制系统，以克服上述技术问题。

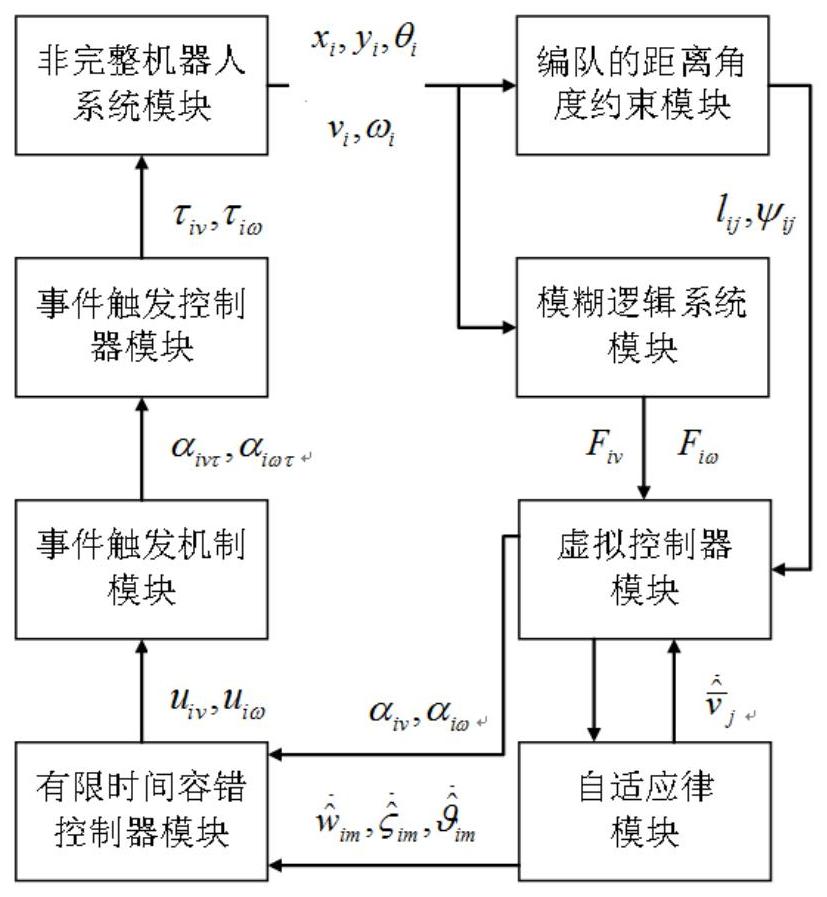
2、一种非完整机器人编队的有限时间事件触发容错控制系统，包括非完整机器人系统模块、模糊逻辑系统模块、编队的距离角度约束模块、虚拟控制器模块、自适应律模块、有限时间容错控制器模块、事件触发机制模块以及事件触发控制器模块，

3、所述非完整机器人系统模块用于获取事件触发后的控制信号，并根据所得实际控制信号计算跟随者的线速度和角速度，进而根据所得线速度和角速度调整跟随者自身的位置和航向角，

4、所述模糊逻辑系统模块用于获取跟随者车载传感器得到的自身线速度和角速度信息，并根据所得线速度和角速度信息对未知非线性函数的进行逼近处理，

5、所述编队的距离角度约束模块用于分别设计相对距离和方位角的约束条件，设置跟随者和领导者之间的相对距离期望值和方位角期望值，获取跟随者和领导者的位置和航向角，根据跟随者和领导者的位置和航向角计算出两者之间的相对距离和相对方位角，根据跟随者和领导者之间的相对距离和相对方位角、相对距离期望值和相对方位角期望值计算距离跟踪误差和方位角跟踪误差，根据相对距离和相对方位角的约束条件对距离跟踪误差和方位角跟踪误差进行约束，

6、所述虚拟控制器模块用于获取跟随者与领导者之间的相对距离和方位角以及逼近处理后的未知非线性函数，设计虚拟控制器，根据所获取的跟随者与领导者之间的相对距离和方位角、逼近处理后的未知非线性函数以及虚拟控制器重新对跟随者的线速度和角速度进行计算，

7、所述自适应律模块用于获取跟随者的线速度、角速度和虚拟控制器，并根据跟随者的线速度、角速度和虚拟控制器，计算出模糊控制自适应参数的估计值，

8、所述有限时间容错控制器模块用于获取跟随者的线速度、角速度、虚拟控制器以及模糊自适应参数的估计值，并根据跟随者的线速度、角速度、虚拟控制器以及模糊自适应参数的估计值设计有限时间容错控制器，所述有限时间容错控制器用于对获取跟随者的容错控制信号，

9、所述事件触发机制模块用于根据有限时间容错控制器获取跟随者的容错控制信号，并根据所述容错控制信号设计事件触发机制，

10、所述事件触发控制器模块用于设计连续控制信号，并根据事件触发机制和连续控制信号设计事件触发控制器，所述事件触发控制器用于对从控制器发送到执行器的连续控制信号的传输频率进行限制，

11、所述非完整机器人系统模块的输入端与事件触发控制器模块输出端相连，模糊逻辑系统模块和编队的距离角度约束模块的输入端与非完整机器人系统模块输出端相连，虚拟控制器模块的输入端与模糊逻辑系统模块和编队的距离角度约束模块的输出端相连，自适应律模块的输入端与虚拟控制器模块的输出端相连，有限时间容错控制器模块的输入端与自适应律模块的输出端相连，事件触发机制模块输入端与有限时间容错控制器模块的输出端相连，事件触发控制器模块输入端与事件触发机制模块的输出端相连。

12、优选地，所述非完整机器人系统模块用于根据公式(1)建立非完整机器人系统模型，

13、

14、其中，下标i代表第i个机器人且i＝1,…,m，(xi,yi)是第i个机器人两驱动轮之间的中点在水平坐标系中x轴坐标和y轴坐标，θi是第i个机器人的航向角，vi和ωi分别表示第i个机器人行驶的线速度和角速度，表示施加在第i个机器人上触发后且存在执行器故障的控制扭矩，非完整机器人系统模型中的矩阵定义如下：mib是机器人自身的质量，mio是装有马达轮子的质量，iib，iiω和iim是转动惯量，ri是驱动轮的半径,ai是机器人宽度的一半，di11和di22是阻尼系数，

15、

16、zi＝[vi,ωi]t，mi＝mib+2mio，

17、根据公式(2)、(3)将非完整机器人系统模型中的动力学方程进行转化，

18、

19、

20、

21、

22、其中，miv和miω是与机器人自身特性相关的未知系统参数，fiv和fiω是与线速度vi和角速度ωi相关的未知线性函数，其中，τiv(t)和τiω(t)表示施加在第i个机器人上的执行器，ρivk(t)∈[0,1]和ρiωk(t)∈[0,1]表示执行器发生故障的失效率，ζivk(t)和ζiωk(t)表示执行器故障中的未知函数部分，k＝1,2,3...表示执行器出现的第k个故障，ρivk(t)＝1,ζivk(t)＝0和ρiωk(t)＝1,ζiωk(t)＝0表示第i个机器人的执行器没有发生故障，

23、根据转化后的动力学方程获取跟随者的线速度和角速度，进而根据公式(1)调整跟随者自身的位置和航向角。

24、优选地，所述模糊逻辑系统模块用于根据模糊逻辑系统和对系统的未知线性函数fiv和fiω进行逼近处理，并假设未知非线性函数为：

25、

26、

27、其中，和为模糊逻辑系统的理想参数，是理想参数的估计，xi＝[vi,ωi]t是需要近似的变量，εiv(xi)和εiω(xi)为理想的机器人系统特性与实际机器人系统中未知非线性函数之间的最小模糊逼近误差，且εiv(xi)满足εiω(xi)满足和为正常数。

28、优选地，所述编队的距离角度约束模块用于根据公式(8)、(9)计算跟随者和领导者之间的相对距离和相对方位角，

29、

30、

31、其中，lij和ψij分别表示第i个机器人与第j个机器人之间的相对距离和相对方位角，是反正切函数，i和j分别表示编队模型中的跟随者和领导者，(xi,yi)是第i个机器人两驱动轮之间的中点在水平坐标系中x轴坐标和y轴坐标，(xj,yj)是第j个机器人两驱动轮之间的中点在水平坐标系中x轴坐标和y轴坐标，θi是第i个机器人的航向角，

32、根据公式(10)、(11)设计相对距离和方位角的约束条件，

33、

34、

35、其中，lmax表示保持通信交流的最大距离，lmin表示避免发生碰撞的最小距离，ψmax表示搜索视野的最大范围也是跟随者与领导者之间的最大方位角，t表示时间，

36、根据公式(12)、(13)计算距离跟踪误差和方位角跟踪误差，

37、zil(t)＝lij(t)-lijd(t) (12)

38、ziψ(t)＝ψij(t)-ψijd(t) (13)

39、其中，lijd(t)和ψijd(t)分别表示跟随者与领导者之间相对距离和相对方位角的期望值，

40、根据公式(14)、(15)对距离跟踪误差和方位角跟踪误差进行约束，

41、lmin-lijd(t)＜zil(t)＜lmax(t)-lijd(t) (14)

42、-ψmax-ψijd(t)＜ziψ(t)＜ψmax-ψijd(t) (15)

43、基于指定性能控制方法，定义zil(t)和ziψ(t)的不对称时变性能约束为：

44、

45、

46、其中，δil(t)＞0和δiψ(t)＞0是设计的边界函数，设计如下的指定性能函数φin(t)为：

47、

48、其中，φil,0＝lmax-lijd，φiψ,0＝ψmax-ψijd，φin,∞是性能函数的稳态边界，φin,0＞φin,∞＞0,ξin＞0，将编队跟踪误差进行归一化即将不对称时变性能约束转化为等式约束，设计转换后的误差变量为

49、

50、将不对称时变性能约束(16)代入(19)，则时不变约束可描述为

51、-δin(t)＜sin(t)＜1，n＝l,ψ (20)

52、在编队控制过程中，对跟踪误差采用时变非对称约束，根据公式(21)使机器人实现轨迹跟踪，公式(21)为障碍函数，

53、

54、其中，和sin是提前设计的边界函数,它们与sin(t)的关系为

55、优选地，所述虚拟控制器模块用于根据公式(22)、(23)、(24)、(25)设计动态虚拟误差面，

56、ziv＝vi-αivf (22)

57、ziω＝ωi-αiωf (23)

58、zαv＝αivf-αiv (24)

59、zαω＝αiωf-αiω (25)

60、其中，zαv和zαω是滤波误差，αivf和αiωf是一阶低通滤波器中间信号变量且满足关系和其中ιiv＞0和ιiω＞0是给定常数，滤波前后信号初值的关系为αivf(0)＝αiv(0)，αiωf(0)＝αiω(0)，

61、选择如下的李亚普诺夫函数：

62、

63、

64、其中，gim＝|mim|ρimk，是参数估计误差，是设计矩阵，γim，rim是设计参数，其中m＝v,ω，

65、设计虚拟控制器αiv和αiω为：

66、

67、

68、其中，n＝l,ψ，λil1，λil2，λiψ1和λiψ2是正的设计参数，tanh(·)是已知的双曲正切函数，＞0是给定常数，vj是领导者线速度，是vj的未知上界，是的估计值，且存在关系

69、优选地，所述自适应律模块用于根据公式(30)、(31)、(32)、(33)计算出模糊控制自适应参数的估计值，

70、

71、

72、

73、

74、其中，rim，γim，λiwm＞0，和是设计参数，ωim是设计矩阵。

75、优选地，所述有限时间容错控制器模块用于根据公式(34)、(35)设计容错控制器uiv(t)，uiω(t)，

76、

77、

78、其中，

79、λi1＞0，λi10＞0，λi2＞0，λi20＞0，σiv＞0，σiω＞0，λiz＞0是设计参数。

80、优选地，所述事件触发机制模块的事件触发机制为，

81、tiv(k+1)＝inf{t∈r||zivτ(t)|≥λv1|τiv(tivk)|+λv2} (36)

82、tiω(k+1)＝inf{t∈r||ziωτ(t)|≥λω1|τiω(tiωk)|+λω2} (37)

83、式中，zimτ(t)＝τim(t)-αimτ(timk)是在时间间隔[timk,tim(k+1))内测量的触发误差，αimτ(timk)是连续控制信号，0≤λm1≤1和λm2＞0是设计参数，其中m＝v,ω。

84、优选地，所述事件触发控制器模块用于根据公式(38)设计有限时间事件触发容错控制器，

85、

86、

87、设计中间连续控制信号为：

88、

89、

90、其中，λv3＞0是设计参数。

91、本发明提供一种非完整机器人编队的有限时间事件触发容错控制系统，具有以下有益效果，第一，本发明基于有限时间控制方法，设计了有限时间容错控制器，此方法可以有效补偿无限次间接性未知执行器故障的影响，并且控制器不需要获取不同故障和未知系统参数的信息。第二，本发明通过设计事件触发机制可以实现非完整多机器人编队有限时间自适应控制，同时合理地减少了控制器的执行次数，节省了网络通信资源。第三，本发明考虑了不确定系统参数和动力学中的未知函数问题，使用模糊逻辑系统对未知的非线性函数进行逼近处理，从而更好地适应在实际中复杂多变的环境及自身发生的变化。第四，本发明使用了指定性能函数与障碍函数对跟随者与领导者之间的相对距离和方位角进行约束，实现两者的碰撞的避免和连通性的维护，保证了机器人在有效的交流范围内的安全性问题。