一种分布式无人机集群自组织轨迹追踪控制算法

本发明属于无人机集群控制，尤其涉及一种分布式无人机集群自组织轨迹追踪控制算法。

背景技术：

1、对于无人机集群来说，精确的轨迹跟踪是一个挑战，它需要跟踪参考轨迹，同时每架无人机都要避免与其他无人机在游动中发生碰撞。无人机集群轨迹跟踪算法通常可分为集中式和分布式两种方法。与集中式方法相比，分布式方案不需要中央节点控制，更加灵活。无人机需要在每个控制周期内跟踪更新后的轨迹。典型的轨迹跟踪方案通常采用分层方式实现，其中外环用于沿参考轨迹生成制导律，内环用于控制精确运动。将轨迹跟踪问题划分为位置环和姿态环，引入高阶滑模观测器来估计位置环中的集总扰动，并构建两个环的控制器来实现精确跟踪。在分层控制方法中，计算得到的控制输入通常来自无人机的当前位置、历史位置和跟踪误差，以及缺乏对其未来状态的预测。

2、基于模型预测控制(mpc)的方法将无人机动力学和参考轨迹转化为最优问题，并根据无人机的动力学特性预测其位置，减小跟踪误差。mpc方法也可以有效地应用于非线性无人机系统，其中使用反馈或前馈线性化技术将非线性动力学转换为线性积分器模型。考虑差分平整度的特点，将mpc与前馈线性化控制相结合，使飞行器能够平滑地跟踪轨迹。上述方法主要考虑单架无人机的轨迹跟踪问题。在无人机集群中，无人机在进行轨迹跟踪时还需要避免与其他无人机发生碰撞，特别是对于大型无人机集群来说，群体轨迹跟踪更具挑战性，尤其是对于大规模无人机集群。

3、生物启发的群体算法已用于大规模群体跟踪，比如与领导者跟随方案相结合的羊群模型，引导群体沿轨迹运动。只有领导者拥有视觉辅助系统，使用算法重新规划路径，其他无人机在无gps环境下预测并跟随领导者的轨迹完成导航任务，并且可以在虚拟领导者中加入动力学来约束无人机集群的运动。虽然结合羊群模型和领导者跟随方案的算法可以引导群体沿着参考轨迹移动，但是领导者的异常状态会导致群体偏离期望的轨迹。

技术实现思路

1、本发明的目的在于提供一种分布式无人机集群自组织轨迹追踪控制算法，旨在解决现有的无人机集群控制算法会导致群体偏离期望轨迹的问题。

2、本发明是这样实现的，一种分布式无人机集群自组织轨迹追踪控制算法，所述方法包括以下步骤：

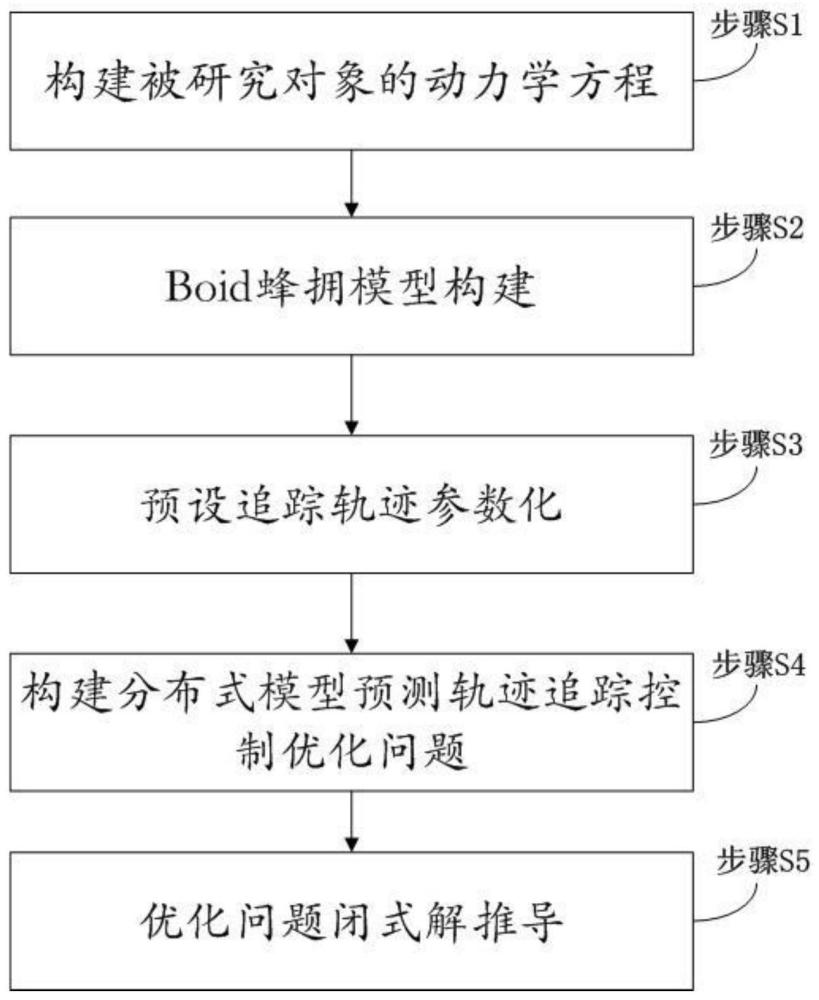
3、步骤s1：构建被研究对象的动力学方程，被研究对象为若干个同构的四旋翼飞行器组成的无人机集群，对于一个由n架无人机组成的集群，其表示为集合其中每架无人机的动力学方程具有以下形式：

4、

5、其中pi，vi，ui∈rm分别表示集群中第i架无人机的位置、速度和控制输入，考虑无人机的控制是周期性的，则(1)式可以基于采样周期ts离散化，得到：

6、

7、集群中无人机之间通过通信网络进行信息交互，通信网络由无向图表示，其中ε表示集群内的无人机，v表示集群中两个无人机是否建立通信连接，每架无人机只能与在通信范围rc内的邻近无人机进行通信，因此通信网络定义为对于第i架无人机，可与其进行通信的邻近无人机用数学表达式为

8、步骤s2：boid蜂拥模型构建，根据reynolds’s boid蜂拥控制模型的定义，其为每个无人机构建分离、对齐及聚合的三个局部交互规则，第i个无人机在每个控制周期内的控制输入ui与相邻无人机的位置和速度相关，boid模型的对齐规则表示为:

9、

10、分离和聚合规则是为了让第i架无人机与它的邻近机保持期望的安全距离d0，因此这两个规则可以整合为一个数学表达式如下:

11、

12、步骤s3：预设追踪轨迹参数化，导航任务前规划的参考轨迹引导无人机集群从起始位置移动到目标位置，同时避免与障碍物碰撞，使用p次b样条曲线来表示参考轨迹，其定义如下:

13、

14、式中c(u)为结点，pl为第一个控制点，nl，p(u)为第l个b样条基函数，ωl为第l个控制点pl的权值；

15、步骤s4：构建分布式模型预测轨迹追踪控制优化问题，根据追踪轨迹和biod蜂拥模型，集群中的每架无人机都遵循相同的优化问题：

16、minji(k)＝ji，p(k)+ji，v(k)+ji，u(k)，    (6)

17、

18、

19、

20、其中ji，p(k)是与无人机位置相关的代价函数，公式(7)中第一项遵循biod规则中的分离和聚合规则，对应于公式(4)，第二项是参考轨迹对无人机位置的引导项，促使无人机跟随着参考轨迹移动，ji，v(k)为速度协同项，遵循对齐规则，对应公式(3)，ji，u(k)为控制输入最小化项，常数α，β，χ，λ是各优化项的权重；

21、步骤s5：优化问题闭式解推导，对等式约束(2)进行变换，并将其合并到成本函数中，因此，将无人机动力学(2)改写为紧凑的形式：

22、xi(k+1)＝axi(k)+bui(k)，  (10)

23、其中

24、

25、式中xi(k)表示第i架无人机及其邻近无人机在k时刻的状态集合为第i架无人机的邻近无人机数量，id为d阶单位矩阵，为无人机的控制量组成的矩阵，式(10)也可以重构为扩展形式：

26、

27、其中

28、

29、然后，将优化问题(6)重构为矩阵形式：

30、minji(k)＝tr[qi(k)tqi(k)]+λtr[ui(k)tui(k)]  (14)

31、其中

32、

33、公式(15)中ri为关系矩阵，用于计算第i架无人机与其邻近无人机和参考轨迹之间的状态差，其定义为：

34、

35、向量1d是由d个1组成的列矢量，公式(16)中ei(k)为期望状态，包括与邻近无人机保持固定的d0距离，速度对齐，以及移动到参考轨迹点，e(k+l|k)的计算取决于状态x(k+l|k)，它满足下面的假设：

36、在dmpc的每个预测期内，第i架无人机无法获得其邻近无人机的控制值，这意味着uj(k+l|k)三0，l＝0，1，...，hp-1，所以对于第i架无人机，它的邻近无人机j的预测状态为

37、xj(k+1)＝axj(k)，  (18)

38、式中

39、经过上述一系列转换后，优化问题(14)包含在所有具有动力学约束的预测周期中无人机状态与期望状态之间的误差，因此可以得到封闭形式的解如下：

40、

41、由于最优解序列中的第一个解通常被选择为第i架无人机在下一时刻的系统输入，因此

42、

43、式中

44、本发明的进一步技术方案是：步骤s1中，在k时刻与第i个无人机保持通信的无人机构成子图

45、本发明的进一步技术方案是：三个局部交互规则定义为：

46、分离：避免集群内个体之间发生碰撞；

47、对齐：每个个体的运动状态会尽可能倾向于与邻近个体一致；

48、聚合：每个个体会尽可能向着群体中心移动，避免群体分离成多个子群体。

49、本发明的进一步技术方案是：步骤s3中，参考轨迹在已知环境的基础上使用经典的规划算法获得，比如a*和d*，之后使用(6)对规划的轨迹进行参数化。

50、本发明的进一步技术方案是：步骤s4中，自导航任务开始，每架无人机的参考轨迹点pr(k)在固定时间tt＝mhpts时同步更新，m∈n+。

51、本发明的有益效果是：该算法使用去中心化的控制方式，便于算法拓展至大规模无人机集群，参照生物群体中蜂拥行为，通过设计简单的控制规则对集群内单架无人机的控制，进而使得无人机集群的轨迹追踪，考虑集群内部无人机的通信范围和安全距离，使得无人机通过与邻近无人机的信息交互，有效避免集群内部碰撞，确保飞行安全，集群内无人机可达成一致性共识，能够确保集群中各个无人机之间保持一致性，促使集群在追踪参考轨迹的同时形成稳定的集群结构，具备灵活性，适用于不同环境和任务需求，优化算法考虑能源效率和计算开销，确保在大规模集群中的实际应用具有可行性。