基于动态控制障碍函数与自适应最优控制的移动机器人

本发明涉及机器人避障，具体涉及基于动态控制障碍函数与自适应最优控制的移动机器人。

背景技术：

1、随着自动化和智能化技术的飞速发展，移动机器人、机械臂和无人机等智能体在工业、服务以及探索等众多领域发挥着越来越重要的作用。其中，智能体的安全避障成为热门研究对象，确保机器人安全高效地在复杂环境中进行路径规划和避障是实现其自主移动功能的关键。

2、目前常见的是基于d-cbf的避障方法正变得更加高效和可靠，最新的研究成果，如结合mpc-d-cbf的方法，已经被国际学术会议接受，展示了其在安全关键型避障中的应用潜力。结合mpc和d-cbf，可以在每个控制步骤中考虑未来的系统状态，并优化出一个既安全又高效的控制序列，但面临复杂环境与不确定性时，mpc存在无法快速响应的问题，同时该方法中对于模型的精确度要求较高，在使用过程中过于依赖点云数据，而结合d-cbf与自适应动态规划算法的控制方法，则是通过将动态障碍函数生成一种安全约束编入代价函数，将安全避障问题转化为最优控制问题。现有技术中存在着用于巡检无人机的自主避障方法存在无法完成障碍物自主绕行、目标检测距离短、计算量大以及避障反应不及时的问题。

技术实现思路

1、为了解决上述技术问题，本发明的目的在于提供基于动态控制障碍函数与自适应最优控制的移动机器人，所采用的技术方案具体如下：

2、本发明一个实施例提供了一种基于动态控制障碍函数与自适应最优控制的移动机器人，包括处理器和存储器，所述处理器用于处理存储在所述存储器中的指令以实现如下监测过程：

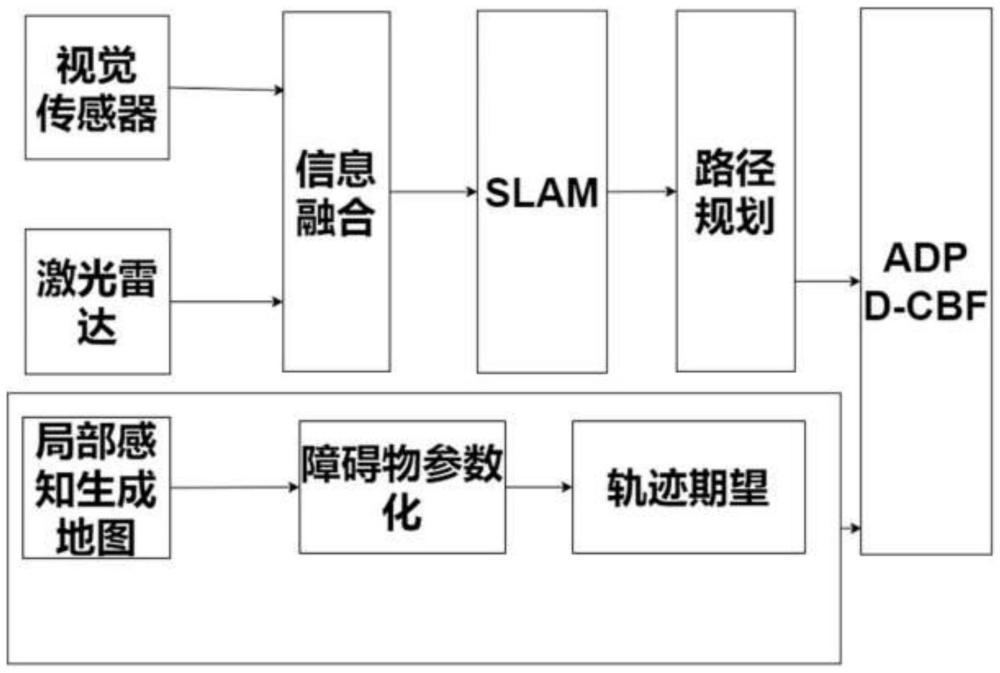
3、通过视觉传感器与激光雷达对环境进行感知与检测，获取环境信息，并进行slam模块的定位与建图；对视觉传感器与激光雷达信息融合，将slam模块接收点云生成tf，实时维护三维概率图，根据pf-rrt*和地图生成参考路径获取路径规划所需地图；

4、分别定义机器人位置、障碍物位置和障碍物形状；基于实时点云检测障碍物，进行聚类操作，对于障碍物，结合障碍物位置和障碍物形状信息参数化为边界椭圆进行封闭，得到障碍物边界椭圆和对应的障碍物运动轨迹；

5、结合自适应动态规划算法与动态避障算法，对未来期望轨迹进行预测，结合障碍物运动轨迹和机器人参数，计算机器人最佳运动方向与运动速度，通过自适应动态规划算法在路径规划所需地图上生成最佳控制策略。

6、进一步地，所述分别定义机器人位置、障碍物位置和障碍物形状；基于实时点云检测障碍物，进行聚类操作，对于障碍物，结合障碍物位置和障碍物形状信息参数化为边界椭圆进行封闭，得到障碍物边界椭圆，包括：

7、分别定义机器人位置、障碍物位置和障碍物形状为xc、s和p；

8、机器人位置xc前方各类障碍物形状位置参数不同，结合障碍物位置的点云数据位置参数s，障碍物形状p，可以成其障碍物的边界椭圆；

9、障碍物位置s由空间坐标(s1，s2，s3)表示，障碍物的边界椭圆参数则由点云信息进行检测生成，形状数据则根据障碍物最长边界增加扩展量，定义椭圆长轴，生成障碍物边界椭圆。

10、进一步地，所述障碍物运动轨迹的获取方法为：

11、结合用卡尔曼滤波对障碍物的运动状态进行估计和预测，基于每个障碍物对应的障碍物边界椭圆，在前向时域内得到一组障碍物边界椭圆，作为障碍物运动轨迹。

12、进一步地，所述结合自适应动态规划算法与动态避障算法，对未来期望轨迹进行预测，结合障碍物运动轨迹和机器人参数，计算机器人最佳运动方向与运动速度，包括：

13、根据未来时刻t1、未来时刻t2和障碍物运动轨迹，计算机器人最佳期望位姿；时刻t1的最佳位置由障碍物质心之间的连线，以及障碍物自身运动方向求得，并记录时刻t1下，机器人最佳期望位姿信息为(x1，y1，p)，其中，x1，y1分别为机器人最佳期望位姿的横坐标和纵坐标，p为机器人最佳期望位姿的方向。

14、进一步地，所述结合自适应动态规划算法与动态避障算法，对未来期望轨迹进行预测，结合障碍物运动轨迹和机器人参数，计算机器人最佳运动方向与运动速度，还包括：

15、机器人的安全性由动态避障函数保障。

16、进一步地，所述机器人的安全性由动态避障函数保障，包括：

17、由于动态避障函数的约束，将机器人位置的中心与障碍物边界椭圆连接，障碍物边界椭圆的外围到机器人位置的距离可记为di(t+nj∣t)，得到距离集，其中t为初始时刻，t+nj为从初始时刻t开始之后的第nj时刻；该距离集扫描cbf区域，并受到cbf区域的边界约束，防止机器人过快地接近障碍物。

18、进一步地，所述结合自适应动态规划算法与动态避障算法，对未来期望轨迹进行预测，结合障碍物运动轨迹和机器人参数，计算机器人最佳运动方向与运动速度，还包括：

19、对机器人的控制采用自适应动态规划算法获取最优控制率。

20、进一步地，所述结合自适应动态规划算法与动态避障算法，对未来期望轨迹进行预测，结合障碍物运动轨迹和机器人参数，计算机器人最佳运动方向与运动速度，还包括：

21、将避障函数作为一种约束加入最优控制的代价函数中；

22、其中，代价函数j(x,u)：

23、

24、其中，x(τ)为变量为τ系统状态矩阵；u(τ)为变量为τ控制策略；r(x(τ),u(τ))为变量为x(τ)和u(τ)的效用函数；t为初始时刻；

25、x表示系统状态矩阵，u为控制策略，通过自适应动态规划算法近似求解最优控制策略；

26、效用函数r(x,u)：

27、r(x,u)＝x′*q*x+u′*r*u+b(x)              (2)

28、q和r为正定矩阵；x′表示系统状态矩阵x的转置矩阵，u′表示控制策略u的转置；

29、r＝1；

30、动态避障函数约束：

31、inf b(x)>＝0,lim b(x)＝∞,b(0)＝0             (3)

32、b(x)为动态避障函数；inf表示无穷大难以表示的数值浮点数；

33、其中x∈inf c,

34、对于安全临界控制，定义c为来连续可微函数h(x)的超水平集，动态避障函数拥有比避障函数更为严格的约束；

35、

36、动态避障函数的设计要遵循这一原则；

37、根据边界椭圆设计建立安全距离ds，椭圆外围距离到li(k)；

38、h(x)＝||p(k)-xob(k)||2-li(k)-ds              (5)

39、p(k)＝[x(k),y(k)]；p(k)为k时刻机器人位置，p(k)＝[x(k),y(k)]中x(k)，y(k)代表的是k时刻机器人位置的x坐标和y坐标；

40、xob(k)＝[xobi(k),yobi(k)]为k时刻障碍物中心位置，xobi(k),yobi(k)分别反映了k时刻障碍物的位置信息，xobi(k)为k时刻障碍物的x坐标，yobi(k)为k时刻障碍物的y坐标；

41、k表示未来k步所处的时间段，li(k)代表在k时刻机器人与障碍物边界椭圆的椭圆外围距离，ds代表通过计算预测的机器人与障碍物的安全距离，在h(x)设计完成后，获取障碍函数b(x)；

42、动态避障函数b(x)可被表示为：

43、

44、其中，s(x)为rn→[0,1]是一个自调函数，kp＞0。

45、进一步地，所述结合自适应动态规划算法与动态避障算法，对未来期望轨迹进行预测，结合障碍物运动轨迹和机器人参数，计算机器人最佳运动方向与运动速度，还包括：

46、自适应动态规划算法的具体步骤；

47、步骤一：根据belllman最优性原理，最优代价函数写为系统状态方程可描述为x＝f(x)+g(x)*u。

48、其中，f(x)，g(x)是关于系统状态矩阵x的函数，u为控制策略，系统状态方程也即为非线性系统方程的通式；

49、为了描述轨迹误差可将系统状态矩阵x写为e；

50、步骤二：引入动态安全控制函数d-cbf的br进入价值函数，则：

51、r(x,u)＝x′*q*x+u′*r*u+b(x)；

52、x′表示系统状态矩阵x的转置矩阵，u′表示控制策略的转置；

53、步骤三：满足hjb方程获得最优控制率u*为最优控制率。

54、步骤四；曼哈顿函数表示为通过神经网络进行逼近，目的是对智能机器人控制，通过数学模型表示下列定义的最优值函数。

55、将系统状态矩阵x换做e表示；

56、最优值函数可由神经网络的形式表示为w(t)为真实的神经网络权值，wt(t)为w(t)的转置矩阵，节点层数记录为n，层数越多误差越小，为连续微的激活函数，对最优值函数分别求关于时间t和e的偏导，当激活函数关于t与e的偏导有界，最优控制输入可以描述为将神经网络近似逼近的输入函数和值函数对于t和e的偏导代入曼哈顿函数。

57、步骤五：获得权值更新率w，获得神经网络权值估计动力学方程，实现近似最优控制；

58、

59、神经网络权值更新率a为给定学习率，设定为a＝50，s'为s转置，e'为系统状态矩阵e转置，e为系统状态矩阵，f(e)，g(e)分别为具体智能体系统模型给定的参数；为连续微的激活函数的导数。

60、一种基于动态控制障碍函数与自适应最优控制的移动机器人，包括移动机器人本体，所述移动机器人本体还包括避障装置，所述避障装置包括数据采集器和控制器，所述数据采集器连接所述控制器，所述数据采集器用于通过视觉传感器与激光雷达对环境进行感知与检测，获取环境信息，所述控制器用于进行slam模块的定位与建图，对视觉传感器与激光雷达信息融合，将slam模块接收点云生成tf，实时维护三维概率图，根据pf-rrt*和地图生成参考路径获取路径规划所需地图；分别定义机器人位置、障碍物位置和障碍物形状；基于实时点云检测障碍物，进行聚类操作，对于障碍物，结合障碍物位置和障碍物形状信息参数化为边界椭圆进行封闭，得到障碍物边界椭圆和对应的障碍物运动轨迹；结合自适应动态规划算法与动态避障算法，对未来期望轨迹进行预测，结合障碍物运动轨迹和机器人参数，计算机器人最佳运动方向与运动速度，通过自适应动态规划算法在路径规划所需地图上生成最佳控制策略。

61、本发明实施例至少具有如下有益效果：

62、本发明实施例采用鲁棒局部感知模块对障碍物进行感知和参数化，并基于卡尔曼滤波考虑不确定性预测障碍物轨迹；然后，结合动态控制障碍函数和最优控制自适应动态规划设计安全控制器，生成机器人在动态环境中导航的安全无碰撞轨迹，现实世界的实验避免了不同类型的障碍。

63、相对于非动态障碍函数基于动态控制障碍函数与自适应控制的移动机器人在复杂情况下有较好的应变能力，相对于d-cbf与mpc的智能机器人，d-cbf与adp不需要建立精确模型。基于adp算法在线求解的算法模型，面临时变系统与非线性系统时，adp算法结合神经网络有优秀的处理能力。同时adp算法为前向算法，智能体机载计算机在安全约束下产生必要的运动轨迹。针对大量非线性系统进行快速响应与最优路径最优轨迹规划。