一种考虑单向输入饱和约束和执行器迟滞的压电微定位平台输出反馈控制方法

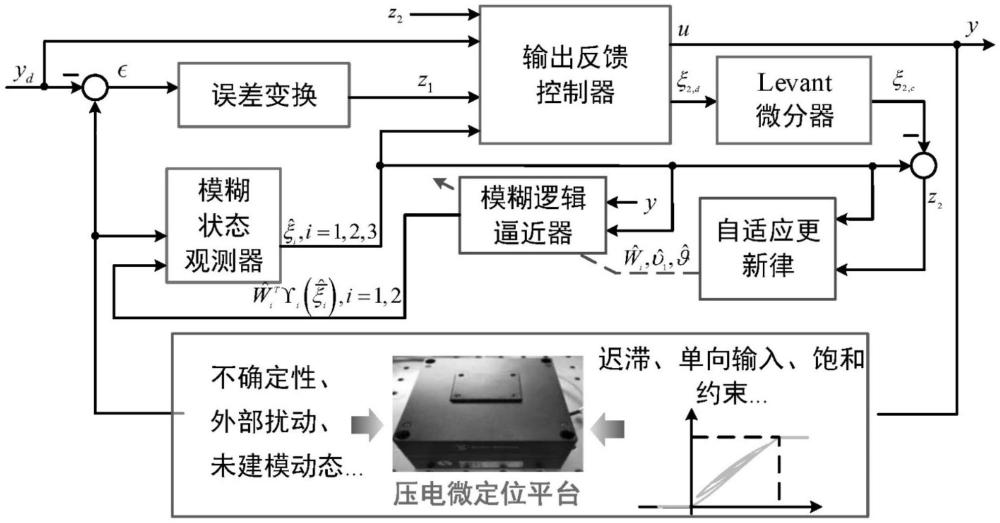
本发明属于压电微定位平台的跟踪控制，具体地，涉及一种考虑单向输入饱和约束和执行器迟滞的压电微定位平台输出反馈控制方法。

背景技术：

0、技术背景

1、随着工程应用对高精密定位技术的需求不断攀升，以智能材料为核心的先进微纳驱动技术备受青睐。压电微定位平台因其纳米级分辨率、高刚度和快速响应等特性而成为微纳驱动领域的关注焦点。然而，压电材料的固有物理特性导致了压电微定位平台执行器的迟滞非线性问题，这增加了控制器设计的复杂性，并可能影响系统的稳定性和定位精度。此外，受到物理限制的制约，输入约束也是压电微定位平台所面临的一个不容忽视的挑战。

2、针对系统的迟滞非线性，一种常用应对手段使逆迟滞补偿方法，通过设计逆迟滞补偿器并与系统迟滞环节串联以补偿迟滞非线性。然而，这种方法的控制性能受到逆迟滞补偿器精度的影响。另一种方法是利用自适应技术而不构建逆迟滞模型。然而，对于压电微定位平台这样的输出反馈系统，迟滞非线性的存在使得状态观测器的构建变得困难。对于输入约束，现有的解决方法主要通过构建辅助设计系统来估计输入约束带来的影响，并通过设计容饱和规定控制器实现约束跟踪性能。此外，采用双曲正切函数来近似输入约束，并设计基于神经网络的控制方法来补偿执行器限制也是常用手段。尽管关于迟滞或输入约束的研究发展迅速，但同时考虑这些问题的控制方法仍然是一个棘手的挑战。并且对于压电微定位平台，控制输入被约束为非负，这意味着输入约束应被视为单向的，从而增加了控制器设计的难度。

3、因此，如何构建基于模糊逻辑系统构建迟滞系统的状态观测器，并在此基础上，为压电微定位平台设计满足单向饱和输入约束条件的输出反馈控制器，从而实现系统的高精度跟踪控制，尚未见到相关技术。

技术实现思路

1、本发明的目的在于提出一种考虑单向输入饱和约束和执行器迟滞的压电微定位平台输出反馈控制方法，以克服现有技术中存在的不足。说明：本发明中表示估计量，(·)表示实际量。

2、本发明所采用技术方案的步骤是：

3、步骤1：考虑具有单向输入饱和约束与迟滞非线性的压电微定位平台，将其建立为如下的二阶非线性系统模型：

4、

5、其中，为状态向量；为未知的光滑非线性函数；g1为未知正增益；为可测系统输出；b0为未知正控制增益；di(t),i＝1,2为有界外部扰动；u为控制输入；vω(u)为具有混合非线性的执行器输出，包括单向输入饱和约束与迟滞非线性，表示如下：

6、

7、其中ωm和ω(u)分别表示饱和约束的上界和迟滞非线性，um为执行器输入上界；对式(2)作如下近似表示：

8、vω(u)＝f(ω(u))+δ       (3)

9、其中f(ω(u))为一个光滑函数，δ为混合非线性与其近似值f(ω(u))的偏差；f(ω(u))表示如下：

10、

11、应用中值定理，将f(ω(u))表示为：

12、

13、其中为未知常数，ωθ定义为ωθ＝θω(u)，其中0<θ<1，θ为未知常数，将迟滞非线性ω(u)表示为迟滞模型pi模型的输出如下：

14、

15、其中ρ(h)表示密度函数，ρ0为由密度函数决定的未知常数，h为积分上界，h为阈值，φh[u](t)为pi迟滞算子；将式(5)、(6)代入式(3)，混合非线性可表示为：

16、

17、其中代表单向迟滞输入饱和对系统的影响；最终将式(7)代入式(1)，压电微定位平台可描述为：

18、

19、其中为未知非线性函数，为另一个未知非线性函数，ψ为非零待设计参数；

20、系统(8)满足如下假设条件：

21、a1：参考轨迹yd有界并且光滑，使得存在且有界；

22、步骤2：利用模糊逻辑系统的逼近能力并且引入信号滤波器，构造模糊状态观测器，以估计无法测量的系统状态；

23、定义系统转变为如下形式：

24、

25、其中p＝[p1,p2]t，pi表示正设计参数，b1＝[1,0]t，b2＝[0,1]t，ψ＝[0,ψ]t；

26、存在以下两个模糊逻辑系统(10)和(11)逼近系统(8)的两个未知非线性函数和

27、

28、

29、其中，为的观测值，为拓展输入向量，φh[uf]为以uf为输入的pi算子，uf为从butterworth低通滤波器hl(s)获得的滤波信号，和分别为模糊逻辑系统(10)和(11)的模糊集函数，w1*和w2*分别为模糊逻辑系统(10)和(11)最优权重向量，与为引入观测状态器后的误差，|εi|≤εm,i＝1,2为模糊逻辑系统的逼近误差，εm为逼近误差的最大值；为了方便表示，定义

30、所设计的模糊状态观测器为：

31、

32、其中，表示ξi的估计值，i＝1,2；是wi*的估计值，i＝1,2；并且定义

33、步骤3：基于一阶levant跟踪微分器设计自适应律、虚拟控制律以及预设性能的控制律；通过自适应更新律对模糊逻辑系统估计权值向量和自适应更新：

34、基于模糊状态观测器，压电微定位系统可改写并扩张为：

35、

36、其中为观测器误差；

37、定义如下坐标变换：

38、

39、其中∈为追踪误差；z2为虚拟误差；ξ2,c表示滤波后的虚拟控制律；

40、为了达到预定的性能要求，即严格保证跟踪误差∈在预先设计的衰减边界内，做误差变换如下：

41、

42、其中z1是经过变换后的跟踪误差；λ(t)>0是性能函数，s(z1)是衰减正定函数；

43、为了防止“微分爆炸”问题，使虚拟控制律通过一阶levant微分器，微分器定义如下：

44、

45、其中μ2,1与μ2,2为正设计参数，ι2,1为中间变量，和为一阶levant微分器的输出；一阶levant微分器对ξ2,d滤波得到滤波器误差满足条件：其中为常数；

46、虚拟控制律ξ2,d设计为：

47、

48、其中κ和k1为正定设计参数；为的估计值；

49、与的更新律设计为：

50、

51、

52、

53、其中γ1,c1,与是正参数；为的估计值，为模糊逻辑系统逼近未知函数l的最优权重向量，不同于系统(8)的两个未知非线性函数和函数l定义为逼近函数l的模糊逻辑系统为其中，为此模糊逻辑系统的模糊集函数，为逼近误差，为模糊逻辑系统输入；

54、引入投影算子proj(·)保证参数与在预先指定的有界集合内，因此更新律改进为：

55、

56、

57、步骤4：设计实际有界控制律u设计为：

58、

59、其中k2为正设计参数。

60、基于步骤2中设计的模糊状态观测器(12)，将步骤3中的虚拟控制律(17)、控制律(23)和自适应更新律(18)，(19)，(20)，(21)，(22)代入李雅普诺夫函数的导数中，通过选取合适的设计参数，可以保证闭环系统收敛在预设的衰减边界(15)内；

61、为闭环系统定义的李雅普诺夫函数如下：

62、

63、其中：

64、

65、闭环系统李雅普诺夫函数的导数

66、

67、其中：

68、γ为二阶正定矩阵；

69、

70、相关设计参数按照如下原则选取：

71、对于模糊状态观测器，其增益pi,i＝1,2应按照劳斯-赫尔维茨准则选取，从而使矩阵a为赫尔维茨矩阵；参数选择为：p1＝1.7，p2＝0.9；

72、对于一阶levant微分器的设计参数μ2,1和μ2,2，其值应根据实际系统情况在0.0001到0.1的范围内选取，本发明的一阶levant微分器设计参数取值为：μ2,1＝0.001，μ2,2＝0.001；

73、性能函数选取为λ(t)＝44e-20t+6；butterworth滤波器设计为

74、对于自适应律、虚拟控制律以及控制律：设计参数k1,k2,ψ的取值影响闭环系统的稳定性，并且取值范围可由李雅普诺夫稳定性理论确定；c1和的取值影响自适应律的调节效果；参数选择为：k1＝30，k2＝2，ψ＝-1，c1＝1.1，

75、本发明的有益效果为：

76、本发明考虑了单向输入饱和约束和执行器迟滞对压电微定位平台的影响，并提出了一种输出反馈控制方法。该方法具有以下三个主要优点：一是充分考虑了执行器迟滞和单向饱和输入约束的实际问题，并采用迟滞描述模型和控制输入转换的方法来解决了执行器复杂的非线性问题。二是通过最大化模糊逻辑系统的逼近能力，并引入信号滤波器和迟滞算子来构建模糊状态观测器。在此基础上，设计了预期性能的动态面控制器，以实现高精度、预定的跟踪性能，克服了现有技术中构建精确迟滞解析逆模型困难以及自适应估计迟滞非线性导致控制器复杂化的缺陷。三是引入了边界控制的概念，构造对数李雅普诺夫函数，并通过选择适当的参数使控制输入满足执行器输入饱和约束。保证了控制信号的先验有界性，从而提高了压电微定位平台运行中的安全性。本研究的控制方法考虑了压电微定位平台在实际应用中面临的执行器迟滞和单向饱和约束问题，为其在实际工程中的应用提供了理论基础和技术参考。